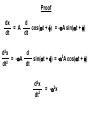* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Simple Harmonic Motion - White Plains Public Schools
Velocity-addition formula wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Center of mass wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Faster-than-light wikipedia , lookup
Routhian mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Fictitious force wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Classical mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Jerk (physics) wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Brownian motion wikipedia , lookup
Work (physics) wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hunting oscillation wikipedia , lookup
Classical central-force problem wikipedia , lookup
Seismometer wikipedia , lookup
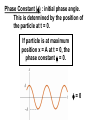
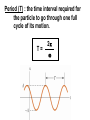
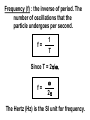
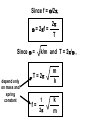
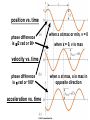
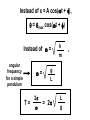
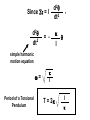
Oscillations Unit 7 Lesson 1 : Simple Harmonic Motion Fs = -kx (Hooke’s Law) Fs is a restoring force because it always points toward the equilibrium position (x = 0) Applying Newton’s Second Law : SF = max -kx = max k ax = x m Simple Harmonic Motion An object moves with simple harmonic motion whenever its acceleration is proportional to its position and is oppositely directed to the displacement from equilibrium. Example 1 A block on the end of a spring is pulled to position x = A and released. In one full cycle of its motion, through what total distance does it travel ? _____ A/2 _____ A _____ 2A _____ 4A dv dt Since a = d2x dt2 = - d2x , = dt2 k m x Notice that the acceleration of the particle in SHM is not constant. It varies with position x. If we call k/m = w2, d2x dt2 = -w2x d2x 2x = -w dt2 (second-order differential equation) We need a function x(t) whose second derivative is the same as the original function with a negative sign and multiplied by w2. One possible solution is : x(t) = A cos(wt + f) Proof dx d = A cos(wt + f) = -wA sin(wt + f) dt dt d2x d 2A cos(wt + f) = -wA sin(wt + f) = -w dt2 dt d2x dt2 = -w2x x(t) = A cos(wt + f) Amplitude (A) : maximum value of the position of the particle in either the positive or negative direction. Angular Frequency (w) : number of oscillations per second. Since k/m = w2, w= k m Phase Constant (f) : initial phase angle. This is determined by the position of the particle at t = 0. If particle is at maximum position x = A at t = 0, the phase constant f = 0. f=0 Pen traces out cosine curve x(t) = A cos(wt + f) Period (T) : the time interval required for the particle to go through one full cycle of its motion. T= 2p w Frequency (f) : the inverse of period. The number of oscillations that the particle undergoes per second. f= 1 T Since T = 2p/w, f= w 2p The Hertz (Hz) is the SI unit for frequency. Since f = w/2p, 2p w = 2pf = T Since w = depend only on mass and spring constant k/m and T = 2p/w , T = 2p f= 1 2p m k k m Velocity in Simple Harmonic Motion dx d = A cos(wt + f) = -wA sin(wt + f) dt dt v = -wA sin(wt + f) Acceleration in Simple Harmonic Motion d2x d 2A cos(wt + f) = -wA sin(wt + f) = -w dt2 dt a = -w2A cos(wt + f) Maximum Speed in Simple Harmonic Motion Since sine and cosine oscillate between +/- 1, vmax = +/- wA vmax = k m A (magnitude only) Maximum Acc. in Simple Harmonic Motion amax = +/- w2A amax = k m A (magnitude only) position vs. time phase difference is p/2 rad or 90o when x at max or min, v = 0 when x = 0, v is max velocity vs. time phase difference is p rad or 180o acceleration vs. time when x at max, a is max in opposite direction Example 2 An object oscillates with simple harmonic motion along the x-axis. Its position varies with time according to the equation x = (4.00 m) cos(pt + p/4) where t is in seconds and the angles in the parentheses are in radians. a) Determine the amplitude, frequency, and period of the motion. b) Calculate the velocity and acceleration of the object at any time t. c) Using the results of part b, determine the position, velocity, and acceleration of the object at t = 1.00 s. d) Determine the maximum speed and maximum acceleration of the object. e) Find the displacement of the object between t = 0 and t = 1.00 s. Example 3 A 200 g block connected to a light spring for which the force constant is 5.00 N/m is free to oscillate on a horizontal, frictionless surface. The block is displaced 5.00 cm from equilibrium and released from rest, as shown below. a) Find the period of its motion. b) Determine the maximum speed of the block. c) What is the maximum acceleration of the block ? d) Express the position, speed, and acceleration as functions of time. e) The block is released from the same initial position, xi = 5.00 cm, but with an initial velocity of vi = -0.100 m/s. Which parts of the solution change and what are the new answers for those that do change ? Example 4 : AP 1989 # 3 A 2 kg block is dropped from a height of 0.45 m above an uncompressed spring, as shown above. The spring has an elastic constant of 200 N/m and negligible mass. The block strikes the end of the spring and sticks to it. a) Determine the speed of the block at the instant it hits the end of the spring. b) Determine the period of the simple harmonic motion that ensues. c) Determine the distance that the spring is compressed at the instant the speed of the block is maximum. d) Determine the maximum compression of the spring. e) Determine the amplitude of the simple harmonic motion. Example 5 : AP 2003 # 2 An ideal spring is hung from the ceiling and a pan of mass M is suspended from the end of the spring, stretching it a distance D as shown above. A piece of clay, also of mass M, is then dropped from a height H onto the pan and sticks to it. Express all algebraic answers in terms of the given quantities and fundamental constants. a) Determine the speed of the clay at the instant it hits the pan. b) Determine the speed of the pan just after the clay strikes it. c) Determine the period of the simple harmonic motion that ensues. d) Determine the distance the spring is stretched (from its initial unstretched length) at the moment the speed of the pan is a maximum. Justify your answer. The clay is now removed from the pan and the pan is returned to equilibrium at the end of the spring. A rubber ball, also of mass M, is dropped from the same height H onto the pan, and after the collision is caught in midair before hitting anything else. e) Indicate below whether the period of the resulting simple harmonic motion of the pan is greater than, less than, or the same as it was in part c. ____ Greater than ____ Less than Justify your answer. ____ The same as Lesson 2 : Energy in Simple Harmonic Motion KE of Block KE = ½ mv2 Since v = -wA sin(wt + f), KE = ½ mw2A2 sin2(wt + f) Elastic PE Energy Stored in Spring U = ½ kx2 Since x = A cos(wt + f), U = ½ kA2 cos2(wt + f) Total Mechanical Energy of Simple Harmonic Oscillator E = KE + U E = ½ mw2A2 sin2(wt + f) + ½ kA2 cos2(wt + f) Since w2 = k/m, E = ½ kA2 [sin2(wt + f) + cos2(wt + f)] Since sin2q + cos2q = 1, E = ½ kA2 E = ½ kA2 The total mechanical energy of a simple harmonic oscillator is a constant of the motion and is proportional to the square of the amplitude. U is small when KE is large, and vice versa. KE + U = constant E = ½ kA2 Since E = KE + U, ½ kA2 = ½ mv2 + ½ kx2 Solving for v, v = +/- k (A2 – x2) m Since w = v = +/- w k m A2 – x2 , velocity of simple harmonic oscillator Example 1 The amplitude of a system moving in simple harmonic motion is doubled. Determine the change in the a) total energy b) maximum speed c) maximum acceleration d) period Example 2 A 0.500 kg cart connected to a light spring for which the force constant is 20.0 N/m oscillates on a horizontal, frictionless air track. a) Calculate the total energy of the system and the maximum speed of the cart if the amplitude of the motion is 3.00 cm. b) What is the velocity of the cart when the position is 2.00 cm ? c) Compare the kinetic and potential energies of the system when the position is 2.00 cm ? Lesson 3 : Comparing Simple Harmonic Motion with Uniform Circular Motion As the turntable rotates with constant angular speed, the shadow of the ball moves back and forth in simple harmonic motion. Reference Circle Simple harmonic motion along a straight line can be represented by the projection of uniform circular motion along a diameter of a reference circle. t=0 Since q = wt = f , x coordinate is x(t) = A cos(wt + f) Point Q moves with simple harmonic motion t>0 Q is the projection of P Example 1 What is the amplitude and phase constant (relative to an x axis to the right) of the simple harmonic motion of the ball’s shadow ? _____ 0.50 m and 0 _____ 1.00 m and 0 _____ 0.50 m and p _____ 1.00 m and p Example 2 While riding behind a car traveling at 3.00 m/s, you notice that one of the car’s tires has a small hemispherical bump on its rim, as shown. a) Explain why the bump, from your viewpoint behind the car, executes simple harmonic motion. b) If the radii of the car’s tires are 0.300 m, what is the bump’s period of oscillation ? Lesson 4 : The Pendulum A simple pendulum exhibits periodic motion. It consists of a particlelike bob of mass m suspended by a light string of length L that is fixed at the upper end. Forces acting on bob Tension in string Gravitational force mg Ft = mg sinq always acts opposite to the displacement of the bob Ft is a restoring force d2s Ft = -mg sinq = m dt2 Since s = Lq and L is constant, d2q g =dt2 L sinq for small values of q d2q g =dt2 L sinq same form d2x dt2 = - k m x For small amplitudes (q < about 10o), the motion of a pendulum is close to simple harmonic motion. Instead of x = A cos(wt + f), q = qmax cos(wt + f) Instead of w = angular frequency for a simple pendulum w= T= 2p w k m g L = 2p L g , w= g L T = 2p L g The period and frequency of a simple pendulum depend only on the length of the string and the acceleration due to gravity. (Period and frequency are independent of mass.) Example 1 Christian Huygens (1629-1695), the greatest clockmaker in history, suggested that an international unit of length could be defined as the length of a simple pendulum having a period of exactly 1s. a) How much shorter would our length unit be had his suggestion been followed ? b) What if Huygens had been born on another planet ? What would the value of g have to be on that planet such that the meter based on Huygen’s pendulum would have the same value as our meter ? Example 2 A simple pendulum has a mass of 0.250 kg and a length of 1.00 m. It is displaced through an angle of 15.0o and released. What is the a) maximum speed b) maximum angular acceleration c) maximum restoring force ? Example 3 A simple pendulum is 5.00 m long. a) What is the period of small oscillations for this pendulum if it is located in an elevator accelerating upward at 5.00 m/s2 ? b) What is its period if the elevator is accelerating downward at 5.00 m/s2 ? c) What is the period of this pendulum if it is placed in a truck that is accelerating horizontally at 5.00 m/s2 ? The Physical Pendulum A hanging object that oscillates about a fixed axis that does not pass through its center of mass and the object cannot be approximated as a point mass. Gravitational force produces a torque about an axis through O. t = mgd sinq Since St = Ia, - mgd sinq = I d2q dt2 - mgd sinq = I d2q dt2 negative sign because t tends to decrease q (restoring force) If q is small so that sinq is almost q, d2q dt2 = -( mgd I )q = - w2q simple harmonic motion equation w= mgd I Since the period of a pendulum is T= T = 2p Period of a Physical Pendulum 2p , w I mgd Example 4 A uniform rod of mass M and length L is pivoted about one end and oscillates in a vertical plane. Find the period of oscillation if the amplitude of the motion is small. Torsional Pendulum A rigid object suspended by a wire. When the object is twisted, the twisted wire exerts a restoring torque that is proportional to the angular position. t = -kq k is called the torsion constant of the wire Since St = I d2q dt2 d2q dt2 = - , k q I simple harmonic motion equation w= Period of a Torsional Pendulum k I T = 2p I k Example 5 A torsional pendulum is formed by taking a meter stick of mass 2.00 kg, and attaching to its center a wire. With its upper end clamped, the vertical wire supports the stick as the stick turns in a horizontal plane. If the resulting period is 3.00 minutes, what is the torsion constant for the wire ?