* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Basic Theories of the Balance of Payments
Survey
Document related concepts
Transcript
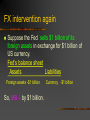
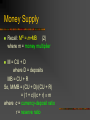
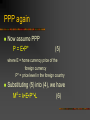
Basic Theories of the Balance of Payments Three Approaches Three Approaches The Elasticities Approach to the Balance of Trade The Absorption Approach to the Balance of Trade The Monetary Approach to the Balance of Payment (MABOP) The Elasticities Approach to BOT d = elasticity of demand = the responsiveness of quantity demanded to changes in price d = (%Qd)/(%P) which is usually negative Elasticities | d | > 1 the demand is elastic | d | < 1 the demand is inelastic If the demand is elastic, the 1% rise in price leads to more than 1% decline in quantity demanded. If the demand is inelastic, the 1% rise in price leads to less than 1% decline in quantity demanded. Devaluation and BOT Does the devaluation of a currency improve the country’s balance of trade? Consider EPs/$ = the Mexican peso price of the dollar Devaluation and BOT (cont’d) (1) If the demand curve for the dollar slopes downward and the supply curve of the dollar slopes upward, then the devaluation of the peso leads to an excess supply of the dollar, which causes the Mexican trade deficit to decrease. Devaluation and BOT (2) If the demand curve for the dollar is steep and the supply curve of the dollar is negatively sloped, then the devaluation of the peso leads to an excess demand for the dollar, which causes the Mexican trade deficit to increase. Devaluation and BOT (cont’d) (1): stable FX market equilibrium (2): unstable FX market equilibrium The case (2) could occur when Mexican demand for US imports and US demand for Mexican exports are both very inelastic. The greater the elasticities of both country’s demand for the other country’s goods, the greater the improvement in Mexico trade balance after a peso devaluation. Devaluation and BOT The condition that guarantees the case (1) is called Marshall-Lerner Condition. J Curve Effect After the devaluation, it is often observed that the trade balance initially deteriorates for a while before getting improved. Elasticities and J-Curves Why do we have a J-Curve? The initial demands tend to be inelastic. Suppose Mexico imports good X from the US and exports good Y to the US. Devaluation Eps/$ PXPs & PY$ Q X d & QY d Elasticities and J-Curves But if Mexican demand for X is inelastic, the % decrease in QXd would be smaller than the % increase in PXPs so that Imports = PXPs QXd would increase. Further, if US demand for Y is inelastic, the % increase in QYd would be smaller than the % decline in PY$ so that Exports = PY$ QYd would fall. Pass Through Devaluation Import prices in the home country and export prices in foreign countries. But prices do not adjust instantaneously. Persistent BOP deficit devaluation Home demand for imports and foreign demand for exports an improvement in BOP in the L-R Pass-through Analysis How do prices adjust to exchange rate changes in the S-R? Differences in the pass-through effect across countries Producers adjust profit margins Example: When the yen appreciated against the dollar substantially during late 1980s, Japanese auto-makers limited the pass-through of higher prices by reducing the profit margins on their products. Pass-though analysis (cont’d) In general, Depreciation of the dollar Foreign sellers cut their profit margins Appreciation of the dollar Foreign sellers increase their profit margins Absorption Approach to BOT Recall the national income identity: Y = C + I + G + (X – M) So Y–A=X–M where A = C + I + G is the total domestic spending or absorption. Absorption approach to BOP (cont’d) If Y > A, then X – M > 0 or BOT > 0. If Y < A, then X – M < 0 or BOT < 0. Does devaluation always improve BOT? Recall: If Y = Y* Full employment level of output, then all resources are already employed and hence, X – M needs A . If Y < Y*, then X – M obtains through increasing Y with A unchanged, i.e. by producing more to sell to foreigners. Absorption approach So, when Y < Y*, devaluation would improve BOT. But when Y > Y*, devaluation would increase X – M but create inflation. Monetary Approach to BOP Recall Current account Non-reserve capital account -------------------------------------Official reserve account money supply Fed’s Balance Sheet Assets Domestic Credit (Treasury securities, Discount loans, etc ) International reserves (Gold, SDR, other foreign currencies denominated deposits and bonds) Liabilities Currency (Fed reserve notes outstanding) Bank reserves Monetary base DC + IR = CU + R MB (1) where DC = domestic credit IR = international reserves CU = currency R = bank reserves MB = monetary base FX intervention again Suppose the Fed sells $1 billion of its foreign assets in exchange for $1 billion of US currency. Fed’s balance sheet Assets Liabilities Foreign assets -$1 billion So, MB by $1 billion. Currency -$1 billion Money Supply Recall: MS = m•MB (2) where m = money multiplier M = CU + D where D = deposits MB = CU + R So, M/MB = (CU + D)/(CU + R) = (1 + c)/(c + r) m where c = currency-deposit ratio r = reserve ratio Money supply and Money demand Substituting (2) in (1), we obtain MS = m (DC + IR) (3) Consider Money demand function: Md = k•P•L (4) where P = price level at home and L is the liquidity preference function, which depends on income and the interest rate. k is a constant. PPP again Now assume PPP P = E•P* (5) where E = home currency price of the foreign currency P* = price level in the foreign country Substituting (5) into (4), we have Md = k•E•P*•L (6) Monetary equilibrium In equilibrium, Md = MS. So, from (3) and (6), we have k•E•P*•L = m (DC + IR) In terms of “% changes” (or growth rates), E^ + P*^ + L^ = w•DC^ + (1-w)•IR^ where k^ = m^ =0 because they are constants. w = DC/(DC + IR). Finally, Rearranging, we obtain (1-w)• IR^ - E^ = P*^ + L^ - w•DC^ (7) Monetary approach to Balance of payments (MABOP) With a fixed exchange rate (E^ = 0), BOP^ = IR^ = [1/(1-w)]•(P*^ + L^) - [w/(1-w)]•DC^ (8) Fed increases MS (Excess money supply) DC IR BOP Fed decreases MS DC IR BOP Monetary approach to exchange rate (MAER) With a flexible exchange rate (BOP=0), -E^ = P*^ + L^ - w•DC^ (9) Fed increases MS DC E (depreciation) Fed decreases MS DC E (appreciation) Managed float Although exchange rates are market determined in principle, central banks intervene at times to peg the rates at some desired level. When MS or Md changes, the central bank can choose either E^ or IR^ to adjust. Implication of PPP Recall PPP again: P = EP*. With a fixed ex rate, E^ = 0, so P^ = P*^ In other words, when the foreign price level is increasing rapidly, then the home price must follow if we are to maintain the fixed E. Imported Inflation Implication of PPP (cont’d) With flexible rates, E is free to vary so that even when P*^ > 0, P^ can be zero by letting E^ = - P*^, or letting the home currency to appreciate by the same amount as the foreign inflation rate. Views based on MABOP BOP disequilibria are essentially monetary phenomena. Devaluation is a substitute for reducing the growth of domestic credit. Appreciation is a substitute for increasing domestic credit growth.