* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Potential Difference: Path Independence
Work (physics) wikipedia , lookup
Electric charge wikipedia , lookup
Speed of gravity wikipedia , lookup
Lorentz force wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Circular dichroism wikipedia , lookup
Quantum potential wikipedia , lookup
Casimir effect wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Field (physics) wikipedia , lookup
Potential energy wikipedia , lookup
Chemical potential wikipedia , lookup
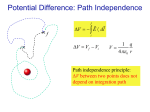
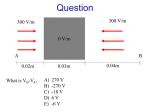
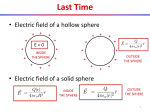
Potential Difference: Path Independence f f i DV = - ò E · dl i DV = Vf - Vi 1 q V= 4pe 0 r Path independence principle: V between two points does not depend on integration path Potential Difference in Metal In static equilibrium What is E inside metal? E = 0 In static equilibrium the electric field is zero at all locations along any path through a metal. f What is the potential difference (Vf – Vi)? f DV = Vf - Vi = - ò E · dl ( i DV = - Ex Dx + Ey Dy + Ez Dz i ) DV = 0 The potential difference is zero between any two locations inside the metal, and the potential at any location must be the same as the potential at any other location. Is V zero everywhere inside a metal? No! But it is constant Potential in Metal In static equilibrium A Capacitor with large plates and a small gap of 3 mm has a potential difference of 6 Volts -Q +Q from one plate to the other. E» E Q/A e0 f DV = - ò E · dl i DV = Ed = 6 V E = (6 Volts)/(0.003 m) = 2000 Volts/m d =3 mm V = 6 Volt Potential in Metal In static equilibrium -Q1 1 mm +Q1 X Insert a 1 mm thick metal slab into the center of the capacitor. Metal slab polarizes and has charges +Q2 and -Q2 on its surfaces. What are the charges Q1 and Q2? At X d =3 mm V = 4 V Charges +Q2 and –Q2 E1 » Q1 / A E2 » Q2 / A e0 e0 E=0 inside metal Q2=Q1 𝐸1 = 𝐸2 Now we have 2 capacitors instead of one Ignoring the fringe fields, E = 2000V/m in each capacitor (from previous slide). DVleft = DVright = ( 2000 V/m ) ( 0.001 m ) = 2 V V inside metal slab is zero! There is no “conservation of potential”! Potential in Metal There can be a potential in metal if is NOT in static equilibrium Metal is not in static equilibrium: • When it is in the process of being polarized • When there is an external source of mobile charges (battery) f DV = - ò E · dl i For each step 𝐸 ∙ ∆𝑙 , the potential difference is: V = -EL If a metal is not in static equilibrium, the potential isn’t constant in the metal. Nonzero electric field of uniform magnitude E throughout the interior of a wire of length L. Direction of the field follows the direction of the wire. Question 300 V/m 300 V/m 0 V/m A B 0.02m What is VB-VA? 0.03m A) B) C) D) E) 270 V -270 V -18 V 6V -6 V 0.04m Question EA = 300 x̂ V / m EB = -300 x̂ V / m 0 V/m A B 0.02m x 0 0.04m 0.03m B .02 DV = VB - VA = - ò E × dl = - ò E × dl A 0 .09 ò E × dl dl = x̂dx .05 V V − −300 𝑉𝐵 − 𝑉𝐴 = − 300 0.02m − 0 m m 𝑉𝐵 − 𝑉𝐴 = −6V − −12V = 6V 0.09m − 0.05m The electric field is uniform in the region below left. The point B is at <0, 0, 0> m. The point C is at <0,-2, 0>m. The potential difference along the path from B to C is ∆𝑉 = +500V. Round Trip Potential Difference + Potential difference due to a stationary point charge is independent of the path Potential difference along a closed loop is zero Predicting Possible Field Configuration Is the following “curly” pattern of electric field possible? f DV = - ò E · dl dl i E is always parallel to dl dl dl DVAA = - ò E · dl = -El = -E2p R ¹ 0 This “curly” pattern of electric field is impossible to produce by arranging any number of stationary point charges! Potential of a Uniformly Charged Ring Q z 2 + R2 Method 1: Divide into point charges and add up contributions due to each charge 1 DQ DV = 4pe 0 r V = å DV = å V= V= 1 DQ 4pe 0 z 2 + R2 1 1 4pe 0 z +R 1 Q 4pe 0 2 2 z2 + R2 å DQ Potential of a Uniformly Charged Ring Q z 2 + R2 Method 2: Integrate electric field along a path z V = - ò E · dl ¥ z V = -ò ¥ Ez = 1 ( Qz 4pe 0 R + z 2 V =- ) 2 3/2 1 Qz ( 4pe 0 R 2 + z 1 4pe 0 z Qò ¥ (R ) 2 3/2 z 2 +z ) dz 2 3/2 z é -1 ù V =Qê 4pe 0 ë z 2 + R 2 úû ¥ 1 Q V= 4pe 0 z 2 + R 2 1 dz Potential of a Uniformly Charged Ring Q z 2 + R2 V= 1 4pe 0 Q z2 + R2 What is V for z>>R ? 1 Q V» 4pe 0 z The same as for a point charge! Potential of a Uniformly Charged Disk one ring: DV = DQ 1 4pe 0 z2 + r2 1 Q rDr DV = 2e 0 A z 2 + r 2 R integrate: 1 Q rdr V= 2e 0 A ò0 z 2 + r 2 1 Q é 2 2 ùR V= z +r ë û0 2e 0 A 2prDr DQ = Q A 1 Qé 2 V= z + R2 - z ù û 2e 0 A ë Potential of a Uniformly Charged Disk 1 Qé 2 V= z + R2 - z ù û 2e 0 A ë Can find E: ¶V Ez = ¶z ù 1 Qé 1 Ez = - 1ú ê 2e 0 A ë z 2 + R 2 û ù 1 Qé 1 Ez = 1ê 2 2 ú 2e 0 A ë z +R û Potential Difference in an Insulator Electric field in capacitor filled with insulator: Enet=Eplates+Edipoles Eplates=const (in capacitor) Edipoles,A Edipoles,B A B Edipoles complicated f(x,y,z) 𝐵 ∆𝑉 = − 𝐸 ∙ 𝑑𝑙 𝐴 Travel from B to A: Edipoles is sometimes parallel to dl, and sometimes antiparallel to dl 1 2 3 4 5 Potential Difference in an Insulator Instead of traveling through inside – travel outside from B to A: A Edipoles, average B E · dl ³ 0 𝐴 𝐸𝑑𝑖𝑝𝑜𝑙𝑒𝑠 ∙ 𝑑𝑙 < 0 ∆𝑉𝐴𝐵 = − 𝐵 Enet=Eplates+Edipoles,average Enet< Eplates Effect of dielectric is to reduce the potential difference. Dielectric Constant Electric field in capacitor filled with insulator: Enet=Eplates-Edipoles K – dielectric constant E plates Enet = K E plates Q / A) ( = Enet Q / A) ( = e0 Ke0 Dielectric Constant Inside an insulator: Enet = Eapplied K Dielectric constant for various insulators: vacuum air typical plastic NaCl water strontium titanate 1 (by definition) 1.0006 5 6.1 80 310 Potential Difference in a Capacitor with Insulator B DV = - ò E · dl E plates A DV = Es = s E plates s K Q / A) ( DV = Es = s Ke0 DVvacuum DVinsulator = K Q / A) ( = e0 Potential Difference in Partially Filled Capacitor B d +Q -Q DV = - ò E · dl E plates = - A K DVinsulator A e0 DV = DVvacuum + DVinsulator DVvacuum = s (Q / A) DV = B x (Q / A) e0 (s - d) (Q / A) = d Ke0 (Q / A) e0 [s - d(1 - 1 / K )] x̂ Energy Density of Electric Field Energy can be stored in electric fields Eone _ plate Q / A) ( = 2e 0 Fby _ you = QE = Q (for small s) (Q / A) 2e 0 DU electric = Fby _ you Ds = Q (Q / A) Ds 2e 0 2 1 æQ / Aö ÷÷ ADs DU el = e 0 çç 2 è e0 ø volume E DU el 1 2 = e E Field energy density: (J/m3) 0 D ( volume) 2 Energy expended by us was converted into energy stored in the electric field Energy Density of Electric Field In the previous slide, the “system” is the set of two plates. Work, Wexternal > 0, is done on the system by you – part of the “surroundings.” DEsystem = DKE + DUelectric = Wexternal If the force exerted by you just offsets the attractive force, Fby-plates, so that the plate moves with no gain in KE, DUelectric = Wexternal = Fby _ you Ds Electric Field and Potential 90V 100V x Ex 1 mm ¶V 10 V Ex = »= -10,000 N/C ¶x 0.001 m Exercise Suppose in some area of space V(x,y,z)=x2+yz. What is E(x,y,z)? ¶V E = - ¶V ¶V Ex = Ez = y ¶y ¶x ¶z ( ¶V Ex = =¶x ¶ x 2 + yz ¶V Ey = =¶y ¶ x 2 + yz ¶V Ez = =¶z ¶ x 2 + yz ( ( ¶x ¶y ¶z ) = - ¶ ( x ) - ¶ ( yz ) = -2x 2 ¶x ¶x ) = - ( ) - ¶ ( yz ) = -z ¶ x2 ¶y ¶y ) = - ( ) - ¶ ( yz ) = -y E ( x, y, z ) = -2x,-z,-y ¶ x2 ¶z ¶z Potential Inside a Uniformly Charged Hollow Sphere ¥ VA = VA - V¥ = ò E · dl 1 Q VA = 4pe 0 R A =0 A ¥ B A VB = VB - V¥ = ò E · dl + ò E · dl 1 Q VB = 4pe 0 R In general, integration path may be complex Example 0V ¶V Ex = ¶x 35 V E If an electron moves from rest through a potential difference of 35 V, what would be its kinetic energy? K = 35 eV DU el = -eDV = -35 eV What if we had a proton? K = 35 eV DU el = eDV = -35 eV 0V 35 V E Which particle will move faster? Shifting the Zero Potential In most cases we are interested in V, not the absolute values of V (V f ) + V0 - (Vi + V0 ) = Vf - Vi ¶DV100 V V Ex = 0¶D.x0002 x m 100 V Ex = 0.0002 m 100 V Ex = 0.0002 m E = 5´ 105 N/C E = 5´ 105 N/C E = 5´ 105 N/C