* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download slides - Nicole Immorlica
Market sentiment wikipedia , lookup
Algorithmic trading wikipedia , lookup
Stock market wikipedia , lookup
Short (finance) wikipedia , lookup
Purchasing power parity wikipedia , lookup
Gasoline and diesel usage and pricing wikipedia , lookup
Stock selection criterion wikipedia , lookup
2010 Flash Crash wikipedia , lookup
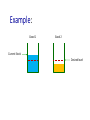
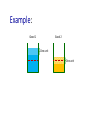
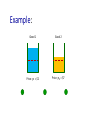
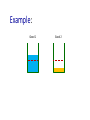
cs234r Markets for Networks and Crowds BRENDAN LUCIER, MICROSOFT RESEARCH NE NICOLE IMMORLICA, MICROSOFT RESEARCH NE Lecture 4: Richard Cole and Lisa Fleischer. Fast-Converging Tatonnement Algorithms for One-Time and Ongoing Market Problems. Preliminary version in ACM Symposium on the Theory of Computing, 2008. Market Convergence Question: how do prices converge? Markets seem to clear quickly and efficiently in practice. Can we reverse-engineer the process? One answer: centralized tâtonnement. This paper: is there a natural non-centralized process? Can we avoid the “invisible auctioneer?” Model Fisher Market: n divisible goods, each from a different seller. • WLOG: one unit of each good m buyers, each with • a budget 𝐵𝑗 • a valuation function 𝑣𝑗 over baskets of goods 𝑣𝑗 (𝑥1𝑗 , … , 𝑥𝑛𝑗 ): buyer 𝑗’s value when obtaining 𝑥𝑖𝑗 quantity of good 𝑖. Model Single-shot Market: 𝐷𝑗 (𝑝1 , … , 𝑝𝑛 ): bundle of goods most preferred by buyer 𝑗, subject to ∑𝑝𝑖 𝑥𝑖𝑗 ≤ 𝐵𝑗 . Assumption: gross substitutes condition (if some prices ↑, demand for other goods not ↓). Price equilibrium: Prices (𝑝1 , … , 𝑝𝑛 ) such that, when each buyer takes 𝐷𝑖 𝑝1 , … , 𝑝𝑛 , all goods are sold. Model: Ongoing Market Each seller has a warehouse that holds the current stock of their good. • 𝑠𝑖 : amount of 𝑖 currently in the warehouse Each round, seller 𝑖: • gets one additional unit of good 𝑖. • sets price 𝑝𝑖 . Buyers buy 𝐷𝑗 (𝒑). Any unsold quantity of good 𝑖 stays in the warehouse until the next round. Example: Good 1 Good 2 Current Stock Desired level Example: Good 2 Good 1 One unit One unit Example: Good 1 Good 2 Price: 𝑝1 = $2 Price: 𝑝2 = $7 Example: Good 1 Good 2 Model: Stability: A vector of prices 𝒑 forms an equilibrium if warehouse quantities are stable over time, and are equal to an “ideal quantity” 𝑠𝑖𝐹 Note: an equilibrium of the one-shot market is also an equilibrium in the ongoing market. Goal: A local price update rule that converges quickly to equilibrium prices. Local: price updates for good i depend only on current supply, past prices, and past demand. Quickly: depends on market parameters. Update Rule: Update prices multiplicatively, in response to over-demand / under-demand. 𝑝𝑖 ← 𝑝𝑖 (1 + 𝜆 ⋅ min 1, 𝑥𝑖 − 1 + 𝜅 𝑠𝑖 − 𝑠𝑖𝐹 Total demand last period for good 𝑖. The demand needed to reduce the warehouse gap by a factor of 𝜅. Parameters 𝜆, 𝜅 ≤ 1 are intended to dampen price changes, to prevent overreaction. Result (informal): Theorem: If 𝜆 and 𝜅 are sufficiently small, relative to the max rate of change in demand with respect to changes in price and budgets, THEN a 𝛿-approximate equilibrium is reached in 1 1 1 POLY log , , 𝛿 𝜆 𝜅 rounds. Analysis Idea: Price rule updates prices in the “right” direction, but slowly enough to avoid oscillation. 𝜆 and 𝜅: set to keep prices in a range where Δ excess demand = Θ Δ pi Each step, update to 𝑝𝑖 is large enough to make constant-factor progress toward equilibrium. Informal Discussion: Motivation: Since price updates depend only on seller-specific feedback, tâtonnement occurs without a centralized market-maker. Questions: • Is this seller behavior justified? • Other models of repeated markets?