* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PH504probclass1a
Potential energy wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Photoelectric effect wikipedia , lookup
History of electrochemistry wikipedia , lookup
Hall effect wikipedia , lookup
Maxwell's equations wikipedia , lookup
Magnetic monopole wikipedia , lookup
Faraday paradox wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Electrostatic generator wikipedia , lookup
Lorentz force wikipedia , lookup
Electric current wikipedia , lookup
Electromotive force wikipedia , lookup
Electric dipole moment wikipedia , lookup
Electricity wikipedia , lookup
Static electricity wikipedia , lookup
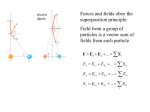
PH504: problems solved in Workshop Class 1. Show that (A + B) (A B) = A2 – B2 and (A + B)(A B) = 2 BA . Verify the above for A = 3i - 5j + 4k and B = i + j + 2k. 2. Consider a solid body in rotation given by v = r where is a constant vector and r is the radial vector. Calculate v . Vorticity is defined as the curl of the velocity vector 3. Consider a long cylinder (e.g. plastic rod) of length L and radius S that carries a volume charge density ρ that is proportional to the distance from the axis s of the cylinder / rod – i.e. ρ(s) = ks where k = proportionality constant. Calculate the total electric charge in the rod. 1. Calculate the ratio of the electrostatic to the gravitational force of attraction of the proton for the electron in a hydrogen atom. 2. A line charge density is given by(x) = 3x3 C m-1. Calculate the total charge contained between x = 0 and x = 1. 3. Consider eight point charges Q located at the corners of a cube of unit length. Calculate the strength of the electric field at a specific point charge due to the other seven charges. In so doing, determine and state the direction of the electric field at a point charge. 1. A positive 1.0 mC charge is located at the origin and a -0.3 mC charge is located at x = 2.0 cm. What is the force on the negative charge? Use: F k q1 q2 r2 Example 1 A positive 1.0 C charge is located at the origin and a -0.3 C charge is located at x = 2.0 cm. What is the force on the negative charge? F k q1 q2 r2 1.0 C 0.0 cm -0.3 C 2.0 cm 6 6 N m2 1.0 10 C 0.3 10 C F 8.99 10 2 C2 0.02m 9 F 6.74 N F 6.74Ni 2. A positive 0.1 mC charge is located at the origin, a +0.2 mC charge is located at (0.0 cm, 1.5 cm), and a 0.2 mC charge is located at (1.0 cm, 0.0 cm). What is the force on the negative charge? Example 2 A positive 0.1 C charge is located at the origin, a +0.2 C charge is located at (0.0 cm, 1.5 cm), and a -0.2 C charge is located at (1.0 cm, 0.0 cm). What is the force on the negative charge? 3 0.2 C (0.0 cm, 1.5 cm) 1 0.1 C (0 cm. 0cm) 2 -0.2 C (1.0 cm, 0.0 cm) q1 q2 F k rˆ 2 r Determine the force between the negative charge and each positive charge. 3 0.2 C (0.0 cm, 1.5 cm) 6 6 N m2 0.110 C 0.2 10 C ˆ F21 8.99 10 i 2 C2 0.01 m 9 1 2 0.1 C (0 cm. 0cm) -0.2 C (1.0 cm, 0.0 cm) F21 180 . Ni The force between charges 1 and 2. F21 k 3 q1 q2 ˆ i 2 r21 0.2 C (0.0 cm, 1.5 cm) 1 0.1 C (0 cm. 0cm) 2 -0.2 C (1.0 cm, 0.0 cm) The force between charges 3 and 2. F23 6 6 N m2 0.2 10 C 0.2 10 C 8.99 10 2 2 C2 0.01m 0.015m 9 F23 111 . N 3 0.2 C (0.0 cm, 1.5 cm) 1 0.1 C (0 cm. 0cm) 2 -0.2 C (1.0 cm, 0.0 cm) Determine the components of each force. F23 F23 cos i F23 sin j F23 111 . N 0.01m i 111 . N 0.015m 0.01m 0.015m 0.01m F23 0.62Ni 0.92Nj 2 3 2 2 0.015m 2 j 0.2 C (0.0 cm, 1.5 cm) 1 0.1 C (0 cm. 0cm) 2 -0.2 C (1.0 cm, 0.0 cm) Determine the sum of the components of the forces. F 180 . Ni 0.62Ni 0.92Nj Determine the resultant force F 2.42 Ni 0.92 Nj F 2.59 N @ 159 from +x axis 2. Determine the final velocity and kinetic energy of an electron released from rest in the presence of a uniform electric field of 300 N/C in the x direction after a period of 0.5 s. Example - Motion of a charged particle in an Electric Field Determine the final velocity and kinetic energy of an electron released from rest in the presence of a uniform electric field of 300 N/C in the x direction after a period of 0.5 s. E F 4.80 10 17 N iˆ -e F F 4.80 1017 N iˆ ˆ a F qE eEi m 9.111031 kg N F 1.60 10 19 C 300 iˆ m C a 5.3 10 13 2 iˆ s Example - Motion of a charged particle in an Electric Field E F K -e m a 5.3 10 13 2 iˆ s v vo at K 1 mv 2 2 1 m 9.1110 31 kg 2.6 10 7 2 s K 3.16 10 16 J m v 0 5.3 10 13 2 iˆ 0.5 10 6 s s m v 2.6 10 7 iˆ s 2 Some more problems: Coulomb’s law and electric field (E-field) 1. A line charge density (x) is given by (x)=3x2 Cm-1. Calculate the total charge contained between the points x=0 and x=L. 1) 2. L3 Coulombs This result is obtained by integrating the equation for (x) between the limits 0 and L. A surface charge density (x,y) is given by (x,y)=3x2+4y2-xy Cm-2. Calculate the total charge contained within the area bounded by x=0+a, y=0+a. 2) 25a4/12 Coulombs This result is obtained by integrating the equation twice with respect to x and y (the order doesn't matter) and using the appropriate limits. 3. A plane circular sheet of radius b has a uniform charge density Cm-2. The E-field at a point P which is a perpendicular distance a from the centre of the sheet is Show that this tends to /20 in the limit of the sheet having an infinite radius. # 4. A line charge extends from x=0 to x=L and has a density (x)=ax Cm-1. Calculate the E-field at a point b (>L) on the xaxis. 4) Split the line charge up into a sequence of point charges of width dx. The size of this point charge is dx=axdx. Calculate the E-field produced at b by this point charge and then integrate the result from x=0 to x=L to find the total E-field. Electric potential energy, electric potential and capacitance 1. The E-field produced by a spherical conductor of radius a and carrying a charge Q is identical to that of a point charge Q placed at the centre of the sphere for r>a and is zero for r<a. Given that (1/2)0E2 is the energy density associated with an Efield, find the total energy associated with the sphere and show that this is equal to (1/2)QV where V is the potential of the sphere. 1) Q2/(80a) Divide the space external to the charge into a series of thin concentric shells of radii r and thickness dr. Energy stored in each shell is (1/2)0E2 multiplied by volume of shell (4r2dr). Use equation for E due to a spherical charge to work out energy stored in each shell then integrate result from infinity to r=a. 2. A capacitor consists of two concentric spheres of radii a and b (b>a). When a charge of +Q is placed on the inner sphere and a charge –Q is placed on the outer sphere the E-field in the region between the spheres is given by where the direction of E is radial. Show that the capacitance of the system is given by 2) Integrate the equation for the E-field between the limits r=b and r=a. This gives the potential difference between the spheres in terms of Q. Compare this result with the definition of capacitance, Q=CV, to find C. The electric dipole 1. An electric dipole consists of an electron and a proton separated by a distance of 1nm. Calculate the electric potential at a point situated along the axis of the dipole, both exactly and using the ideal dipole formula, at distances of 1, 10 and 100nm from the centre of the dipole. Calculate the percentage error that results from the use of the ideal dipole formula in each case. e = 1.602 ´ 10-19 C = 8.8542x10-12 C2 m-2 N-1 Ideal 1.44V, 1.44x10-2V, 1.44x10-4V Exact 1.92V, 1.44x10-2V, 1.44x10-4V Errors 33%, 0.25%, 2.5x10-3% Use the equation from the lecture notes for the ideal case. For the exact case treat the system as two point charges and calculate the potential as the sum of the potentials due to each charge. Gauss's law 1. Calculate the divergence of the following vectors (Cartesian co-ordinates) 2i+3yj+4k, 4x2i, xyi+yzj+zxk 1. 2. 3, 8x, y+z+x Two concentric spherical shells of radii a and b (b>a) carry charges of +Q and -Q respectively. Find the resultant Efield in the regions r<a, b>r>a and r>b. Assume that the charges are spread uniformly over the surfaces of the spheres. 2) For r<a and r>b E=0 for a<r<b E=Q/(40r2). Remember it is only the charge contained within the Gaussian surface that contributes to the flux through the surface. 3. Calculate the electric potentials for the charge distributions of questions 2 and 3. Sketch your results. 3) For the spheres: r>b V=0, b>r>a , for r<a 4. Use Gauss’s law to find the E-field both inside and outside of an infinite plane of thickness a and carrying a uniform charge density . (S) 4) Outside of plane E=a/(20), within plane E=r/(20) where r is the distance from the centre of the plane. When applying a Gaussian surface you need to consider what fraction of the charge is contained within the surface.