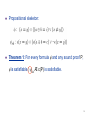Download Slides

A framework for eager
encoding
Daniel Kroening
Ofer Strichman
ETH, Switzerland
Technion, Israel
(Executive summary)
(submitted to: Formal Aspects of Computing)
1

A generic framework for reducing decidable logics to
propositional logic (beyond NP).

Instantiating the framework for a specific logic L, requires
a deductive system for L that meets several criteria.
 Linear arithmetic, EUF, arrays etc all have it.
2

A proof rule:

A proof step: (Rule, Antecedent, Proposition)

Definition (Proof-step Constraint): let A1…Ak be the
Antecedents and p the Proposition of step. Then:
Boolean
encoding
3

A proof P =(s1,…, sn) is a set of Proof Steps,


…in which the Antecedence relation is acyclic
The Proof Constraint c(P) induced by P is the
conjunction of the constraints induced by its steps:
P
C(P)
4

Propositional skeleton:

Theorem 1: For every formula  and any sound proof P,
 is satisfiable ) sk Æ c(P) is satisfiable.
5
Complete proofs

Definition (Complete proofs): A proof P is called
complete with respect to  if
6
Sufficient condition for completeness #1



Notation: A – assumption, B – a proposition.
denotes: P proves B from A.
Let  be an unsatisfiable formula
Theorem 2: A proof P is complete with respect to  if
for every full assignment 
TL(): Theory Literals
corresponding to 
Not constructive!
7

Projection of a variable x: a set of proof steps that
eliminate x and maintains satisfiability.

Strong projection of a variable x: a projection of x that
maintains :
The projected consequences from each minimal
unsatisfiable core of literals is unsatisfiable.
8
Example – strong projection
Consider the formula
U2
U1
Now strongly project x1:
Both sub-formulas are unsatisfiable and do not contain x1.
9

Let C be a conjunction of ’s literals.
A proof construction procedure: eliminate all variables in
C through strong projection.

Theorem 3: The constructed proof is ‘complete’ for .

10

Goal: for a given logic L,




Find a strong projection procedure.
Construct P
Generate c(P)
Check sk Æ c(P)
11
Example: Disjunctive Linear Arithmetic
[S02]
e1
e2
e3
e4
C : x1 - x2 < 0, x1 - x3 < 0, -x1 + 2x3 + x2 < 0, -x3 < -1
e5
2x3 < 0,
e6
x3 + x2 < 0
A proof P by (Strong) projection:
x1: e1  e3  e5
e2  e3  e6
x3: e4  e5  false
4. Solve ’ = sk Æ c(P)
12
What now ?


It is left to show a strong projection method
for each logic we are interested in integrating.
Current eager procedures are far too
wasteful. Need to find better ones.
13