Download Smith Chart

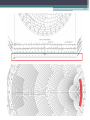
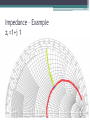
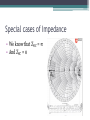
Lecture 18 – 24: Smith Chart
Instructor: Engr. Zuneera Aziz
Course: Microwave Engineering
Introduction
• Invented by Phillip H. Smith
• It is a graphical ‘nomogram’
• Used for solving Transmission line problems
and matching circuits
• Used to represent parameters such as:
Impedance, Admittance, Reflection coefficients,
S parameters, etc.
Introduction
• Plotted on the complex reflection coefficient
plane in two dimensions and is scaled in
normalized impedance, normalized admittance
or both. (Z Smith Charts, Y Smith Charts or YZ
Smith Charts respectively)
• Transmission lines having differing values of Zo
all behave the same, as far as their normalized
impedance properties are concerned.
• The smith chart may also be used for lumped
element matching and analysis problems
Introduction
• The Smith chart is a graphical calculator that allows
the
relatively
complicated
mathematical
calculations, which use complex algebra and
numbers, to be replaced with geometrical
constructs, and it allows us to see at a glance what
the effects of altering the transmission line (feed)
geometry will be. If used regularly, it gives the
practitioner a really good feel for the behavior of
transmission lines and the wide range of impedance
that a transmitter may see for situations of
moderately high mismatch (VSWR).
Normalized impedance at any point
along the transmission line
• The Smith chart lets us relate the complex dimensionless
number gamma at any point P along the line, to the
normalized load impedance zL = ZL/Zo which causes the
reflection, and also to the distance we are from the load
in terms of the wavelength of waves on the line.
• We can then read off the normalized impedance zL at the
point P along the line, where the actual impedance Zo is
the local ratio of total voltage to total current taking into
account the phase angles as well as the sizes. This
impedance is what a generator would "see" if we cut the
line at this point P and connected the remaining
transmission line and its load to the generator terminals.
Normalized impedance at any point
along the transmission line
• Why should the impedance we see vary along the
transmission line? Well, the impedance we
measure is really the total voltage on the line
(formed from the sum of forward and backward
wave voltages) divided by the total current on
the line (formed by the sum of forward and
backward wave currents).
So this is how a Smith Chart Looks Like!
http://sss-mag.com/pdf/smithchart.pdf
This is what you can find from a Smith
Chart
•
•
•
•
•
•
•
•
Reflection Coefficient
VSWR
Transmission Coefficient
Load Impedance
Admittance
Input Impedance
Lmin and Lmax
and even more …
Reflection Coefficient
• The smith chart can be thought of as a circle
(with radius equal to 1)
• This circle is the circle for the Reflection
Coefficient Γ
• The reflection coefficient Γ will possess values
between 0 and 1 (0 for no reflection and 1 for
complete reflection)
• So that means that the Γ should be plotted
inside the unit circle
Reflection Coefficient
• The center of this unit circle is the place where Γ
is 0 (ideally this is what we want!)
• At any point ON the unit circle, Γ = 1 and that
means that all the power is reflected back from
the load (Do we want that? NO!)
A few starter examples
• Γ = 0.5
• Γ = -0.3 + j 0.4
• Γ = -j
• What will be the load impedance if Zo=50 ohms
for the above values of Γ?
The Answers:
• For Γ = 0.5
For ZL:
Which corresponds
to ZL = 150 Ohms
The Answers:
• For Γ = -0.3 + j 0.4
ZL = 20.27 + j 21.62 Ohms
The Answers:
• For Γ = -j
ZL = -j 50 Ohms
A purely capacitive load!
Concept of Normalized Impedances
• Normalized Load Impedance
• To make the Smith Chart more general and
independent of the characteristic impedance Z0
of the transmission line, we will normalize the
load impedance ZL by Z0 for all future plots:
Constant Resistance Circles
• Suppose we have a normalized load impedance
given by:
zL= R + j Y
• Y is NOT the admittance here, Y is any real
number here.
Constant Resistance Circles
• So for different values of
Resistance you the following
circles in the smith chart. For
any one circle, the resistance
will be constant but the
reactance (the imaginary part)
is going to change on the
circumference of that
particular constant resistance
circle.
Constant Reactance Curves
• Now lets hold constant the
reactance (Y) and vary R. This
will result in producing the
following curves on the Smith
Chart. So for a given curve, the
reactance will be same but as
we move ON the curve, we’ll
have different values of
Resistance.
Vary Reactance on Resistance Circle
• In the following example, we
have taken 2 values of
Resistance (R=1.0, 0.3)
• For R=1.0 we have taken X=0
(zL=1+j 0)
• For R=0.3, is taken as 0, 3 and
-0.4. Corresponding to
▫ zL=0.3
▫ zL=0.3+ j 3
▫ zL=0.3-j 0.4
Vary Resistance on a Reactance Curve
• Now here we’re taking
constant reactance of 1.0 and
different resistances (R=0.3
and 2.o) implying to zL=0.3 + j
1.0 and zL=2.0 + j 1.0)
Zero Reactance
• An important curve is given by
Im[zL]=0. That is, the set of all
impedances given by zL = R,
where the imaginary part is
zero and the real part (the
resistance) is greater than or
equal to zero. The result is
shown in Figure.
• It is understood that for Short
Circuit zL=0 and for Open
Circuit zL= ∞
Zero Reactance
•
•
•
•
So the three special cases are:
zL=0+j 0, Γ =1
zL=1+j 0, Γ =0
zL=∞+ j 0, Γ =1
Transmission Coefficients
• The transmission coefficient is given by:
Vtransmitted
T  1  
Vincident
• The inner most axis denotes the Transmission coefficient angle
• The transmission could be easily plotted with the help of
reflection coefficient (taking the same point) and then
calculating the magnitude of the transmission coefficient with
the help of the linear scale
Impedance
• The first thing that should be done is the Normalization of the given
impedance from Zo, in the following manner:
zL 
Zreal jZimaginary
Zo
• Check the point where the Resistance Circle and the Reactance
Curve intersect
• Negative Reactance implies to being Capacitive
• Positive Reactance implies to being Inductive
Impedance - Example
• So lets suppose I have a load impedance ZL =
50 + j 50 ohms, the Characteristic impedance
Zo= 50 ohms
• After I normalize it:
zL= 1 + j 1
• Now let’s plot this on the Smith Chart
Impedance – Example
zL=1+j 1
Impedance – Example 2
• Do the same thing for ZL=50 - j 50
Impedance – Example 2
zL=1- j 1
Finding Reflection coefficient with the
help of zL
• Find the angle of reflection
coefficient by drawing a line
from the center of the smith
chart to the circumference,
crossing the zL point.
• The axis will show you the
angle
• For magnitude, scale the
point from center of the
smith chart to zL and arc it
down on the linear scale of
reflection coefficient
Admittance
•
•
•
•
Lets begin with the previous example:
zL=1+j1 (normalized impedance of the load)
yL = 1/zL
The method is called ‘translating through the
center of the smith chart’
Plotting Admittance
Plotting Admittance
• Now copy the distance of
zL and plot it on the line
from the center of the
smith chart.
• So the yL comes out to be :
0.5 – j 0.5 (in normalized
form)
• To find YL in mhos,
multiply yL by Yo which is
given by Yo = 1/Zo
• So for this example: YL (in
mhos) = 0.01 – j 0.01
mhos
Special cases of Impedance
• We know that ZOC = ∞
• And ZSC = 0
Special Cases of Admittance
• Just translate through the center!
Special Cases of Reflection Coefficient
• ΓOC= 1 ∠ 0°(Plot it at
zOC point)
• ΓSC= 1 ∠ 180° (Plot it
at zSC point)
Input Impedance - Zin
• Go ‘towards the
generator’ in order to
find input impedance.
You are provided with
load impedance and
the length of the
transmission line
(outer most axis)
Input Impedance - Zin
Another way to find ZL
• Now we’d like to find the
load impedance, provided
we have the input
impedance and line length
• Suppose Zin = 100 – j 100
ohms
• zin= 2 – j 2 ohms
Another way to find ZL
• Now move towards the
‘load’ on the 2nd last axis
Another way to find ZL
• Not really a complexity!
• What if you get the length greater than 0.5 λ
such as may be 2.2 λ, 0.61 λ
• The maximum scale is 0.5 λ so you just have to
add up the wavelengths and move around the
smith chart
• Negate the multiples of 0.5 λ from the given
transmission length (if greater than 0.5 λ )
VSWR
• Draw a circle round the zL point
• The value of resistance circle (easily read at the 0
reactance line) represents the VSWR
• You can follow up with the linear scale, where
you can find the value in dB too
VSWR – Lmin, Lmax
Example
• A lossless transmission line is terminated by a
load ZL=10+j20 Ω. Find Γ, T, VSWR, lmin, lmax, YL
and Zin if the line length is 4 cm and frequency of
3 GHz.
Example - Solution
• Step 1: Normalize the load impedance
• zL=0.2+j0.4
• Step 2: Calculate length of transmission line in
number of wavelengths
c 3X 108
 
 0.1m  10cm
9
f 3 X 10
• So the transmission line length in number of
wavelengths is:
4cm
 0 .4 
10cm
Example - Solution
•
•
•
•
Step 3: plot zL
Step 4: Draw a circle through the zL point
Step 5: Find out reflection coefficient
Step 6: Find VSWR (with the circle method and the
linear scale too, both give the same results)
• Step 7: Find yL and then YL (translating through the
center of the smith chart)
• Step 8: find T with the help of reflection coefficient
• Step 9: find zin by rotating towards the generator 0.4
wavelengths