Download Digital Electronics

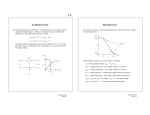
Digital Electronics
■
Assign Ò1Ó and Ò0Ó to a range of voltage (or current), with a separation that
minimizes a transition region
Voltage
Positive Logic
Negative Logic
Logic
1
Logic
0
Transition Region
Transition Region
Logic
0
Logic
1
We will use positive logic (usually the case)
Simplest binary function: inversion
A
B
A
B
0
1
1
0
Circuit must take the Ò1Ó voltage range at the input and deliver the Ò0Ó voltage
range at the output.
EE 105 Spring 1997
Lecture 13
An Ideal Inverter
■
Voltage transfer curve for an inverter -- it should yield 0 V when a high voltage
is input and the high voltage, V+, when a low voltage is input. An ideal inverter
would be very forgiving of imperfect input voltages ...
VIN >VM = V+/ 2 --> VOUT = 0 V
VIN < VM = V+/ 2 --> VOUT = V+
Note that the ideal inverter returns correct logical outputs (0 V or V+) even when
the input voltage is corrupted by noise, voltage spikes, etc. that are nearly half
the supply voltage!
VOUT
V+
V+
+
+
VIN
VOUT
−
−
VOUT = VIN
V +/2
0
0
(a)
VM =
V+
2
(b)
V+
VIN
EE 105 Spring 1997
Lecture 13
Real Inverters
The inverters which we can build are approximations to the ideal inverter. A typical
inverter characteristic is:
VOUT
VMAX
VOH
= −1
VM
VOL
VMIN
0
0
VIL
VM
VIH
V+
VIN
On the output and input axes, several voltages are deÞned:
VM = voltage midpoint where VOUT = VIN = VM.
VOL = Òvoltage output lowÓ = max. output voltage for a valid Ò0Ó
VOH = Òvoltage output highÓ = min. output voltage for a valid Ò1Ó
VIL = Òvoltage input lowÓ = smaller input voltage where slope equals -1
VIH = Òvoltage input highÓ = larger input voltage where slope equals -1
VMAX = VOUT for VIN = 0 V; usually, VMAX = V+, the supply voltage
VMIN = VOUT for VIN = V+ and is the minimum output voltage
EE 105 Spring 1997
Lecture 13
Noise Margins
■
Digital electronic circuits consist of series of logic gates; the voltage signals are
contaminated by ÒnoiseÓ -- actually, mostly generated by capacitive coupling
from other parts of the circuit
vNOISE
1
2
VOH1
NMH
VIH1
Voltage
VOH2
VIL1
VIH2
VIL2
VOL1
NML
VOL2
NMH = VOH − VIH
NML = VIL − VOL
■
Output of inverter #1 is at least VOH1 (assuming it had a valid low input
VIN1 < VIL1); therefore, thereÕs a margin of VOH1 - VIH2 to spare before the input
to inverter #2 has an invalid high input.
■
For the case of cascaded identical inverters, we deÞne noise margins
NMH = VOH - VIH = noise margin (high)
NML = VIL - VOL = noise margin (low)
EE 105 Spring 1997
Lecture 13
Inverter Circuits:
■
NMOS-Resistor Pull-Up
First example: motivate the concept of a MOSFET switch enabling an
approximation to the inverter.
VDD
R
+
VIN
CL
VOUT
_
VDD = 5 V (typically)
CL = load capacitance (from interconnections and from other inverters
connected to the output
VBS = 0 V -- bulk-to-source short-circuit is assumed to be present unless
indicated otherwise
EE 105 Spring 1997
Lecture 13
Finding the Voltage Transfer Curve
■
■
Approach 1: start with VIN = 0 and increase it; Þgure out the operating regions
for the MOSFET and substitute ID = ID (VGS, VDS) = ID(VIN, VOUT) and Þnd
V OUT = V DD Ð I D R
Approach 2: use a graphical technique
>> we know ID(VIN, VOUT) from the MOSFETÕs drain characteristics
>> we can Þnd another equation relating ID and VOUT from KVL --
VOUT = VDD - ID R
ID = (VDD - VOUT) / R
ID
R
+
VOUT
V
_ DD
we donÕt
care what
goes here!
load line
■
Intersections between the family of drain characteristics and the load line yield
VOUT as a function of VIN
EE 105 Spring 1997
Lecture 13
Voltage Transfer Curve using Load Line Technique
■
Graphical intersection of ID versus VOUT characteristics with load line
ID
VIN
VDD
R
VDD
VOUT
* Given µnCox = 50 µA/V2, (W/L) = 4.5/1.5 = 3, VTn = 1.0 V, and λn = 0
VOUT
(V)
Inverter Characteristics
5.0
R = 5 kΩ
R = 25 kΩ
4.0
3.0
2.0
1.0
0.0
0.0
1.0
2.0
3.0
4.0
5.0
VIN
(V)
EE 105 Spring 1997
Lecture 13
Improved Inverters
■
First try: quantify how increasing the resistor R affects the slope of the voltage
transfer curve at the midpoint (a measure of the steepness of the transition
region)
dv OUT
= Av
----------------dv IN
VM
From our small-signal modelling concepts, this slope is equal to the ratio of the
small-signal voltages vout and vin
v out
---------- = A v
v in
How to Þnd vout / vin? Use the small-signal model!
----------------------------------------Small-signal model of the battery VDD --> a short circuit!
Why?
vDD = VDD + vdd ... by deÞnition, an ideal battery has
vDD = VDD which implies that vdd = 0.
EE 105 Spring 1997
Lecture 13
Small-Signal Model of Inverter
*Finding the small-signal circuit, neglecting capacitors:
R
replace with
small-signal
model
VM
short
+
V
_ DD
vOUT = VOUT + vout
CL
+
vin
_
+
VIN = VM
_
short
* No backgate effect generator included
since vbs = 0
R
* gm and ro are evaluated at the bias point:
VGS = VM and the corresponding ID.
+
g
vin
vout
gmvgs
_
ro
s
EE 105 Spring 1997
Lecture 13
Small-Signal Analysis
■
Solving for the small-signal voltage gain -- the slope of the transfer curve at VIN
= VM:
v out
---------- = Ð g m ( R r o ) ≅ Ð g m R = A v
v in
where we have assumed that R << ro, which is reasonable for small λn
■
The transconductance is a function of the DC drain current, which is in turn a
function of R through the load line equation:
g m ≅ 2µ n C ox ( W ⁄ L )I D =
V DD Ð V M
2µ n C ox ( W ⁄ L )  --------------------------


R
so that A v ∝ R
■
Why not increase R to say 500 kΩ? The answer lies in the dynamic response of
the inverter. Tiny DC drain currents --> very slow transitions
Therefore, we want to have a large Av with a large ID ...
EE 105 Spring 1997
Lecture 13