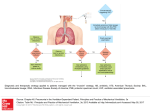
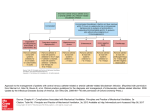
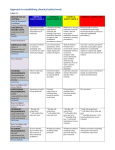
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Single-sided Natural Ventilation: Design Analysis
Earth sheltering wikipedia , lookup
Green building wikipedia , lookup
Sustainable architecture wikipedia , lookup
Land-use forecasting wikipedia , lookup
Rural Khmer house wikipedia , lookup
Thermal comfort wikipedia , lookup
Indoor air pollution in developing nations wikipedia , lookup
Building regulations in the United Kingdom wikipedia , lookup
Passive house wikipedia , lookup
Single-sided Natural Ventilation: Design Analysis and General Guidelines by Camille Allocca B.E., Mechanical Engineering The Cooper Union, 1999 SUBMITTED TO THE DEPARTMENT OF MECHANICAL ENGINEERING IN PARTIAL FULFILLMENT OF THE REQUIREMENTS OF THE DEGREE OF MASTER OF SCIENCE IN MECHANICAL ENGINEERING AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY MASSACHUSETTS INSTITUTE OF-TECHNOLOGY JUL 16 2001 JUNE 2001 LIBRARIES C 2001 Massachusetts Institute of Technology. All rights reserved I BARKER - - ................ Signature of Author ....................... '/ Department of Mechanical Engineering May 23, 2001 .. ...................................... Leon Glicksman Professor of Building Technology & Mechanical Engineering Thesis Supervisor ......... Certified by......................... ....................................................... Qingyan (Yan) Chen Associate Professor of Building Technology Thesis Supervisor Certified by............................. A ccepted by ........................................ ................ Ain A. Sonin Professor of Mechanical Engineering Chairman, Department Committee on Graduate Students Room 14-0551 77 Massachusetts Avenue Cambridge, MA 02139 Miuetbraries Document Services Ph: 617.253.2800 Email: [email protected] http://libraries.mit.edu/docs DISCLAIMER NOTICE The accompanying media item for this thesis is available in the MIT Libraries or Institute Archives. Thank you. SINGLE-SIDED NATURAL VENTILATION: DESIGN ANALYSIS AND GENERAL GUIDELINES by Camille Allocca Submitted to the Department of Mechanical Engineering on May 23, 2001 in Partial Fulfillment of the Requirements for the Degree of Master of Science in Mechanical Engineering ABSTRACT Natural ventilation is an effective measure to save energy consumed in buildings and to improve indoor air quality. This study focuses specifically on the principles of single-sided natural ventilation design. Single-sided ventilation is very common in building designs and has been shown to produce very complicated, fluctuating airflow patterns at the openings of buildings. An ongoing challenge in natural ventilation design is therefore the ability to control the mechanisms of wind and temperature for desirable indoor environment conditions. Understanding these effects is important in determining the feasibility of natural ventilation designs. The current research approach used mainly (CFD) tools, together with analytical solutions, empirical models, and experimental results. CFD models were created and analyzed to determine the validity of using this tool for single-sided ventilation analysis and design. The impact of using computational modeling tools for the development of natural ventilation design is great to the building industry field. The focus of this CFD study was on a single room within a residential building in Cambridge, MA. Simulations were performed under varying conditions of temperature, wind speed, wind direction, opening layout and size, and internal heat load, in order to evaluate parameter trends. Airflow rates, velocity fields, and temperature distributions were derived from analytical equations and empirical models as well as from experimental measurements, in order to validate and perform further research in this area. Consequently, this investigation found CFD tools to be valid for studying single-sided natural ventilation strategies with respect to indoor, outdoor, and combined indoor and outdoor flow. From this validation, CFD was applied further to determine the effects of buoyancy, wind, and combined flow on natural ventilation rates and overall indoor conditions. For buoyancy driven flow, CFD performed well when modeling both the indoor and outdoor environment in the calculation, resulting in a 10% difference between semi-analytical and CFD results. However, for wind-driven flow, CFD was found to underpredict empirical model results by approximately 25%. This underprediction was attributed to mean or time-averaged, rather than instantaneous calculations of the CFD technique applied to this study. In addition to evaluating the effects of buoyancy and wind on ventilationrates, this study also focused on the effects of wind direction, opposing buoyancy and wind forces, and mixed-mode ventilation. The results from these studies provided further insight into the field of single-sided ventilation and revealed the need for further research in this valuable area. To fully understand and utilize this natural ventilation strategy, the results from the complete single-sided ventilation study were compiled and developed into a computer design tool and a set of general design guidelines. These tools were created in such a way so that designers can use them to evaluate ventilation performance and see immediate results for an indoor environment that they propose to design. The level of analysis that is desired by designers in this area calls for a tool such as this one. This total investigation has been essential in evaluating and analyzing the important areas of the single-sided ventilation field and in providing a strong foundation for further research in improving natural ventilation design as well as in improving CFD and turbulence modeling. Thesis Supervisors: Leon Glicksman, Qingyan (Yan) Chen Titles: Professor of Building Technology and Mechanical Engineering, Associate Professor of Building Technology 3p TABLE OF CONTENTS A b stra c t ........................................................................................................................................................ Chapter 1: Introduction................................................................................................................................. 1.1 Statem ent of the Problem ...................................................................................................... 1.2 Single-sided N atural Ventilation Strategies ............................................................................. 1.3 Study Objective and Research Procedure................................................................................ Chapter 2: Literature Review ..................................................................................................................... 2.1 Single-sided V entilation Theory.............................................................................................. 2.1.1 Buoyancy-driven Flow .................................................................................................... 2.1.2 W ind-driven Flow .............................................................................................................. 2.1.3 Com bined Buoyancy and W ind-driven Flow ................................................................... 2.2 A nalytical Methods .................................................................................................................... 2.2.1 Sem i-A nalytical Equations for Buoyancy-driven Flow ................................................... 2.2.2 N etwork M odels ................................................................................................................. 2.3 Experim ental M ethods................................................................................................................ 2.3.1 Em pirical M odels ............................................................................................................... 2.4 Com putational M ethods ............................................................................................................. 2.5 Therm al Com fort and Indoor A ir Q uality .............................................................................. 2.6 M ixed-m ode Single-sided V entilation..................................................................................... 2.7 Conclusions ............................................................................................................................... Chapter 3: CFD Validation......................................................................................................................... 3.1 Introduction ................................................................................................................................ 3.2 CFD Indoor Validation - D isplacem ent Ventilation.............................................................. 3.2.1 Test Facility........................................................................................................................ 3.2.2 General Experim ental Setup............................................................................................ 3.2.3 General CFD Setup............................................................................................................. 3.2.4 Light Welding Shop Case - Experim ental and CFD Results.......................................... 3.2.5 Conclusions ........................................................................................................................ 3.3 CFD Outdoor V alidation - Flow Around a Cube................................................................... 3.3.1 Experim ental and CFD Setup......................................................................................... 3.3.2 Experim ental and CFD Results ....................................................................................... 3.3.3 Conclusions ........................................................................................................................ 3.4 CFD V alidation of Single-sided V entilation ........................................................................... 3.4.1 W ind-driven Single-sided V entilation Experim ent....................................................... 3.4.2 W ind-driven Single-sided V entilation CFD M odel........................................................ 3 7 7 8 10 11 11 11 12 12 13 13 15 16 16 18 20 22 24 25 25 25 26 28 29 31 32 36 36 37 39 39 39 40 3.4.3 Experim ental and CFD Results ....................................................................................... 3.4.4 Conclusions ........................................................................................................................ 3.5 Conclusions ................................................................................................................................ 41 45 45 Chapter 4: Single-sided Ventilation Study.............................................................................................. 46 4.1 Introduction ................................................................................................................................ 46 4.2 Building Design.......................................................................................................................... 46 4.3 Student Residence Room - General CFD Setup ........................................................................ 4.4 Therm al Buoyancy Study........................................................................................................... 4.4.1 Indoor stack m odel ............................................................................................................. 4.4.2 Com bined indoor and outdoor stack m odel..................................................................... 4.4.3 Results and D iscussion.................................................................................................... 4.4.4 Trends in Therm al Buoyancy Study Results.................................................................. 4.4.5 Conclusions ........................................................................................................................ 47 48 48 49 52 53 55 4.5 55 W ind and Stack Study ................................................................................................................ 4 4.5.1 W ind and Stack M odel.................................................................................................... 56 4.5.2 4.5.3 4.5.4 Comparison of Empirical M odels................................................................................... Comparison of CFD and Empirical Results for a Single Opening.................................. CFD and Curve-Fit Empirical Results for an Upper and Lower Opening ...................... 58 59 60 4.6 W ind Direction Study................................................................................................................. 4.7 Counteracting W ind and Stack Study..................................................................................... 4.8 M ixed M ode Ventilation Study .............................................................................................. 4.8.1 Concurrent M ixed Mode Ventilation - Low Cooling......................................................... 4.8.2 Cross Ventilation Duct System....................................................................................... 4 .8 .3 C o n clu sion s ........................................................................................................................ 4 .9 C o nc lu sio n s ................................................................................................................................ Chapter 5: Design Tool and General Guidelines..................................................................................... 5 .1 Intro du ctio n ................................................................................................................................ 5.2 Single-sided Ventilation Design Tool.................................................................................... 62 66 67 68 74 77 77 79 79 79 5.2.1 Design Input - Student Room Case.................................................................................... 80 5.2.2 Outdoor Conditions - Boston TMY Data........................................................................ 81 5.2.3 Design Output - Student Room Case................................................................................. 83 5 .2 .4 D iscu ssio n ........................................................................................................................... 86 5 .2 .5 C on c lu sio n s ........................................................................................................................ 87 5.3 Single-sided Ventilation General Design Guidelines............................................................ 88 5 .4 C o n c lu sio ns ................................................................................................................................ 96 Chapter 6: Conclusions, Recommendations, and Future Work............................................................... 97 6 .1 C o nc lu sion s ................................................................................................................................ 97 6.2 Limitations of the Study and Future Recommendations....................................................... 99 Referen ces..............................................................................................................10 2 Appendix A: Detailed Calculations.................................................................................105 Appendix B: CFD Validation of Displacement Ventilation Case - Cubicle Office..........................112 5 ACKNOWLEDGMENTS I would first like to thank Professor Qingyan (Yan) Chen and Professor Leon Glicksman for all their advisement, knowledge, support, and encouragement. They have both provided me with a wealth of knowledge and guidance and that I will value and take with me in the future. I would like to thank the U.S. National Science Foundation for funding my research focusing on natural ventilation studies, a field that has huge present and future importance and worth. I would also like to thank Yi Jiang and John Zhai for all their time and knowledgeable help in the fields of natural ventilation and CFD. Your help and infinite kindness have meant a great deal to me. Thank you to everyone in the Building Technology Program for making this a great environment to be a part of. Finally, I would like to thank my family for their encouragement, support, and love. Thanks for all your patience and understanding. Camille Allocca May 2001 6 CHAPTER 1: INTRODUCTION 1.1 Statement of the Problem In the building industry, there has been a recognized need for sustainable development. This means that building designers must satisfy the needs of today's users without compromising the ability of future generations to meet their own needs. Buildings impose long-term impacts on the environment. Mechanical ventilation and air conditioning of buildings consume large amounts of energy in the world, especially in developed countries, where buildings are responsible for one third of all energy consumption [1]. This increased use of mostly fossil-based energy leads to atmospheric pollution and global warming. The design of energy-efficient buildings requires a balance between good thermal performance and acceptable indoor air quality. Natural ventilation is an energy efficient alternative for reducing the cooling loads in buildings, achieving thermal comfort, and maintaining a healthy indoor environment [2,3,4]. Typically, the energy cost of a naturally ventilated building is 40% less than that of an air-conditioned building [5]. Natural ventilation, therefore, contributes to a sustainable environment by reducing energy use in buildings. Recent surveys have suggested that some building occupants prefer spaces that are naturally lit and ventilated. The survey results concluded that 89% preferred buildings that were not air-conditioned [6]. This is under the assumption that the building can provide acceptable air quality and thermal comfort to its occupants. The most important factors in the design of a building are good daylighting and ventilation created by opening windows. In the same survey, 67% of the building managers were concerned with specific strategies to reduce energy costs. Good daylight, natural ventilation, and low energy costs are all features of a properly designed energy-efficient building. Natural ventilation, the focus of this study, must be carefully analyzed at the design stage in order to determine the feasibility and benefits of using this design strategy. There are two main types of natural ventilation: cross and single-sided ventilation. In both cases, the driving forces are wind and buoyancy. Differences in wind pressure along the facade and differences between indoor and outdoor temperatures create a natural air exchange between indoor and outdoor air. The air movement through a building depends on the strength and direction of these forces and the resistance of the flow path. These physical processes are complex, and predicting their effectiveness is a difficult task. The challenge of natural ventilation design is to control these various mechanisms in order to obtain the required indoor environment conditions. Cross ventilation is generally more effective in providing adequate air movement than single-sided ventilation. However, single-sided ventilation configurations are very common, especially in urban environments. This is due to the fact that the high density of urban construction imposes an arrangement involving small spaces that are not interconnected, or spaces with one exposed facade, where cross ventilation is not possible [7]. Many office, educational, and residential buildings are designed for singlesided ventilation. However, the performance of single-sided natural ventilation is not well understood, making it difficult to effectively design for this strategy. Although most designs for single-sided ventilation focus on the effects of this buoyancy-driven flow, the steady effects and turbulent nature of wind, which create airflow fluctuations at the openings, also play a significant role, and must also be analyzed to better understand the full potential of single-sided ventilation. There is a particular lack of information in the area of combined effects of wind and buoyancy on single-sided ventilation. For these reasons, it is important to fully understand and analyze this form of 7 natural ventilation in order to make its design more effective. A focus of this study has therefore been to analyze the effects of wind and temperature, both separately and combined, as well as many other design features of single-sided natural ventilation. Maximizing ventilation rates is one way in which to significantly enhance single-sided ventilation through improvements on the design. In addition to maximizing airflow rates, some other design variables that were considered for optimum single-sided ventilation in the current study are depth of a space, window layout and size, building orientation, and internal heat loads. These parameters greatly infhence the temperature field, airflow field, and thermal comfort conditions within a particular space, and must therefore be optimized by the designer for ventilation and thermal comfort. Some of these strategies are discussed in the following section, which provides an overall discussion on effective natural ventilation strategies. Many of these strategies were applied to the single-sided ventilation analysis in the current study, although some were not addressed. 1.2 Single-sided Natural Ventilation Strategies The layout and form of a naturally ventilated building must be designed to assist a desired airflow strategy, that of maximizing available airflow. The strategy must then be implemented so that the air can flow along the chosen path at the required flow rates under natural available conditions. Fresh air must flow from outside, through the occupied space, and then to the exhaust point. Therefore, a natural ventilation system is generally made up of three components: . . . The ventilation inlets where fresh air is drawn into the building A flow path through the space to the exhaust point The outlet, where the air is exhausted outside the building Figure 1 shows that natural ventilation restricts the plan of the building, in that all theventilated spaces must be within a certain maximum distance from the inlet or outlet. This constraint also allows natural light into much of the space, and contributes to occupant satisfaction. outlet inlet flow path Figure 1: Schematic of single-sided natural ventilation "system" Certain issues need to be considered when designing for natural ventilation, such as: . Natural ventilation design must satisfy appropriate thermal comfort and air quality requirements for occupants throughout the space. 8 * * Outdoor conditions must be favorable for indoor thermal comfort in order to implement natural ventilation. The geometry, size, and layout of window openings must maximize the natural ventilation potential for a building. More specifically, * * * * Site layout and building orientation have a significant impact on indoor conditions of a building. Prevailing wind directions must be taken into consideration in order to optimize the natural ventilation potential of the site. In addition, good solar control may be obtained by orienting buildings with their main facades facing north and south, making it much easier to protect these surfaces from excessive solar gain in the summer. The depth of a space is critical in the allowance of fresh air into the building. There is an upper limit on this allowable depth, beyond which fresh comfortable air is unable to penetrate the space. This is due to the fact that air flowing across a space picks up heat and contaminants. For this same reason, the higher a space is, the higher the contaminants and heat will be displaced above the occupied zone, and the better the quality of the air will be in terms of both temperature and pollution. The furniture layout and any internal partitions should allow easy access to all ventilation openings so that natural airflow can be easily controlled and flow is not restricted. High ventilation rates can create drafts at a level that disturbs papers. Designing the windows to open above desk height can reduce this effect. Other important elements of natural ventilation design involve areas that are not purely based on ventilation. Although these issues were not directly addressed in the current study, they are important and should therefore be considered: * * * * * * Thermal capacity should be considered in the form of exposed ceilings and floors in order to dampen the effect of fluctuations in heat gain. A high thermal capacity structure can achieve some energy recovery by absorbing excess heat gains during the day and rejecting this heat at night. The location of ventilation inlets must be carefully evaluated due to outdoor gaseous pollutant sources. Since inlets and outlets are typically evenly distributed over the building facade, it is challenging to locate all the inlets away from sources of pollution. Natural ventilation systems allow outside generated noise into a building. Therefore, there is a need to provide for acoustic privacy without compromising the free flow of natural ventilation across a space. If a ventilation strategy relies on opening windows, the designer needs to consider security issues, especially if the windows are left open overnight for nighttime cooling. In addition to being advantageous for airflow purposes, the narrower plan depth of naturally ventilated buildings allows greater use of natural lighting. The amount of solar gain entering the building must be minimized to reduce the total heat gain of the space. This can be accomplished by minimizing the glazed areas of facades exposed to direct solar gain (to between 20 and 40%) and using shading, blinds, or solar control glass to achieve good solar protection. However, minimizing the glazed area of facade contradicts the natural ventilation principle of maximizing ventilation, and must be seriously considered. All the issues discussed need to be considered when designing for single-sided natural ventilation. By considering these issues early on, during the design stage, a designer can avoid the obstacle of having to mend consequential problems later on. 9 1.3 Study Objective and Research Procedure There is a need to better understand the complex flows of single-sided ventilation in order to introduce more effective designs into buildings. This can be accomplished through experimental, analytical, and numerical studies. Experimental results are valuable in determining how a specific physical process behaves. The measurements obtained from experimental methods can then be used to derive more general theoretical and analytical models. These models can provide guiding rules for a limited range of applications similar to that of the experiments upon which the models are based. However, for this reason, analytical methods can usually only deal with simple cases of flow through openings. The final study, that of numerical techniques, such as computational fluid dynamics (CFD), allows for the modeling of a wider array of flow phenomena, ranging from simple to complex cases. However, this method requires validation with experimental studies in order to have full confidence in the numerical results. All of these methods are important in fully understanding the physics of natural ventilation and will each be addressed in this study. Computational fluid dynamics (CFD) has been an integral part of this study. For the case of natural ventilation, CFD makes it possible to optimize the indoor airflow distribution by changing parameters during the design stage. One particular advantage of computational modeling for the case of single-sided natural ventilation is that parameters influencing airflow in a space, such as wind and buoyancy effects, can be evaluated both separately and collectively. It is difficult to separate wind and buoyancy forces during measurement in a real building. In this study, therefore, CFD modeling has been the focus in predicting airflow and temperature properties in single-sided naturally ventilated spaces. Another part of this study will enable designers to use the information obtained from the singlesided ventilation analysis in order to produce improved designs. This is possible through the use of a simplified design tool, and a set of general guidelines, which were developed in the final stages of this study. The computer design tool predicts the indoor conditions resulting from a particular inputted design and local weather data, while the guidelines provide a step-by-step procedure to designers, which enables them to simply evaluate their designs to obtain potential ventilation rates. The current study was organized in the following manner: . * * . . A literature review of the existing research and information available on single-sided natural ventilation. A CFD validation of both indoor and outdoor flow, as well as validation of a specific singlesided ventilation experiment from the literature. A detailed single-sided ventilation study, focusing on CFD modeling of a particular space. This study also incorporates theoretical, analytical, and empirical results. A set of guidelines and a design tool for further analysis of single-sided ventilation designs. Conclusions made from the study, including assumptions made and limitations present. Chapter 2 discusses the background of single-sided ventilation, focusing on the effect of buoyancy and wind. This chapter also discusses the theoretical, analytical, experimental, and modeling work thathas been performed in this area of study. Chapter 3 discusses the results from several CFD validation cases that strengthen the results of the current study. In Chapter 4, the procedure and results from the current study are discussed and analyzed. Chapter 5 shows the resulting tools that were developed from this study and sample results from various cases. The final chapter, Chapter 6 makes concluding remarks on the outcome and limitations of this study and makes recommendations for future work. Collectively, these chapters provide an in-depth analysis of the principles, design issues, limitations, and possible improvements in designing for single-sided natural ventilation. 10 CHAPTER 2: LITERATURE REVIEW Single-sided natural ventilation is driven by the forces of temperature and wind, which both play a significant role in single-sided ventilation. However, the physical phenomenon of each of these forces, as well as their combined effects, is complex and not fully understood. Despite the fact that single-sided ventilation is found more frequently in building designs, the study of single-sided ventilation has been given far less attention and analysis than has cross ventilation. It is therefore necessary to understand in more detail the effect of the outside natural environment on an indoor environment with single-sided natural ventilation. An overview of the separate and combined effects of temperature and wind forces on single-sided ventilation is given in this chapter. In addition, a literature review of the various analytical, experimental, and computational studies performed on single-sided ventilation is provided in this chapter as a background for the current study. This will offer a foundation upon which further analysis will be presented in the following chapters. Issues relevant to single-sided natural ventilation and alternative design options are also presented in this chapter. 2.1 Single-sided Ventilation Theory The two major physical parameters affecting airflow in single-sided natural ventilation are the temperature difference across the opening(s) and the wind forces. Single-sided ventilation depends on the interaction of these parameters, which creates pressure differences across the openings(s), driving the air inside/outside the ventilated space. 2.1.1 Buoyancy-driven Flow Temperature differences between the inside and outside of a building and between different spaces within a building produce buoyancy forces that drive the flow in single-sided natural ventilation. The flow is especially evident for a space with (1) a large opening or (2) an upper and lower opening. A temperature difference between the space and the environment causes a density difference, where the warm air is less dense than the colder air. As a result, a pressure difference occurs between the inside and outside air, as shown in Figure 2a. The higher internal pressure at the upper opening drives outflow and the lower internal pressure at the bottom opening drives inflow. This temperature-driven effect is also known as stack effect. The words stack and buoyancy are used interchangeably throughout this study. As inside and outside temperatures equalize, the stack pressure approaches zero and there is no driving force for ventilation. The location of ventilation openings determines the temperature distribution within a space. If two vents are open, one at the top of the space, and the other at the bottom of the space, cool air will flow into the lower opening, and warm air will flow out of the upper opening, as shown in Figure 2b. This type of ventilation, which creates a temperature stratification within the space, is called displacement ventilation. Although it has a much stronger effect for spaces with upper and lower openings, displacement ventilation can also occur in spaces with a single large opening at the mid-height of the room, as shown in Figure 2c. Airflow through such an opening in single-sided ventilation has been an area of great interest because the opening serves as both an air inlet and outlet. Compared with upper and lower openings, however, lower ventilation rates are generated and the ventilated air does not penetrate as far into the space. Displacement ventilation is effective in removing heat and pollutants from the occupied zone by displacing them to the upper part of the room where they then exit the space. Stronger airflow will be induced when there is a large vertical separation between inlets and outlets, and when there is a large difference between indoor and outdoor temperatures. The semi-analytical equations for buoyancy-driven 11 flow through the double and single opening window geometries of Figure 2b and c, respectively, are derived from both Bernoulli theory and empirical coefficients and are discussed in Section 2.2.1. J interior Tou Tin h Tin ; Tout pressure (a) (b) (c) Figure 2: (a) Indoor and outdoor pressure distribution for buoyancy-driven flow 181. Buoyancy-driven flow through (b) an upper and lower opening, (c) a single opening 2.1.2 Wind-driven Flow Single-sided natural ventilation relies on pressure differences across its openings to drive air inside and outside a particular space. The related physical processes are complex, especially for the case of winddriven flow, because of the variability in outdoor wind conditions and the turbulent motion of the wind. Experimental results have shown that the fluctuating effects of the wind are responsible forthe airflow in the case of single-sided ventilation. Fluctuating flows are attributed to the turbulent characteristics of the incoming wind and/or to turbulence induced by the building itself [9]. Turbulence in the airflow along an opening causes simultaneous positive and negative pressure fluctuations of the inside air. This fluctuation of pressure distribution along the surface of an opening is a very important driving force for the case of single-sided ventilation. This variability, however, is not taken into account by Bernoulli theory. According to the Bernoulli theory, the pressure difference variation with height is only attributed to the buoyancy term, (pu,-p 1n)gz, where p is the density of air, g is the acceleration due to gravity, and z is the height. The variation in location and time of wind pressures makes the formation of a corresponding theoretical wind term impossible. The physical description and mathematical interpretation of winddriven flow must therefore be handled by empirical and modeling approaches. 2.1.3 Combined Buoyancy and Wind-driven Flow Due to the complex physics of wind-driven flow, combined wind and stack flow cannot be solved through analytical solutions to the theoretical equations, either. The simultaneous influence of temperature and wind on the ventilation process at an open window is especially unknown because of the difficulty in determining whether wind and stack forces reinforce or counteract each other. Since it is uncertain how temperature and wind interact with and affect each other, reliance must be placed upon experimental and modeling studies, as with wind-driven flow. Simple empirical models have been developed based on experiments and the data-fitting results from these experiments. In the case of CFD models, however, there is a lack of detailed analysis in the area of single-sided ventilation, especially for the case of flow due to combined effects. Experimental and computational methods are necessary tools for better understanding of this combined form of single-sided ventilation. 12 2.2 Analytical Methods In order to study airflow parameters, various analytical methods have been developed. These methods apply Bernoulli theory principles to obtain airflow rate information. One such method involves applying simple equations from Bernoulli theory for buoyancy-driven flow, together with an empirical discharge coefficient, to single-sided ventilation. Network modeling is another analytical method that has been developed extensively and calculates the pressure differences across nodes in the airflows between building zones. These methods are explained in the following sections. 2.2.1 Semi-Analytical Equationsfor Buoyancy-driven Flow The most important parameter for evaluating natural ventilation design is the volume flow rate through the opening(s). Some simple analytical equations with empirical coefficients are available for the determination of the flow rate. The buoyancy-driven pressure difference across an opening, Ap, also referred to as the hydrostatic pressure difference, is a function of the height of the stack and the density difference between the air inside and outside the stack. 1 Ap = -pout 2 - Pin )gh() where Ap is the stack pressure difference, g is the acceleration due to gravity, and h is the height between the incoming and outgoing airflow paths. For buoyancy-driven single-sided ventilation through an upper and lower opening (Figure 2b) of equal area, A, the volume flow rate through each opening, *stack d stack Ap = C A gh Pin (m3/s), is given as -(2) Pin where Cd is taken to be the discharge coefficient, which accounts for viscous losses at the area contraction [10]. The theoretical value of Cd for a sharp edged orifice, such as a doorway, is equal to 0.61 [11]. The equation above assumes the airflow, taken at the center of an opening, to be constant along the opening height, since the airflow profile is nearly constant (see Figure 2b). Since single-sided ventilation is characterized by temperature stratification inside a space, the subscript, in, refers to the average indoor value of the given variable. This isothermal assumption introduces error into this simplified calculation. The subscript, out, refers to the value of the given variable outside the space. The temperature and density differences are approximately related by Out- Pin Pi (Tin - Tout) Tout _ AT Tout(3 valid when AT is small (<10 0 C) [10], with Tout expressed in degrees Kelvin. The term, AT, is used throughout this study to refer to the difference between the outside and the average inside temperature conditions. Using the above approximation, the single-sided volume flow rate for an upper and lower opening setup becomes [10] 13 Ystack =C A (4) h AT For the case where the areas of the upper (At) and lower (Ab) windows are different, the volume flow rate is derived to be Ystack =C A .AT gh (5) T,t where [12] A* =[AAtAb /( At 2 +A 2 )] (6) By applying similar Bernoulli theory principles to single-sided ventilation through a single large opening (Figure 2c), the volume flow rate is calculated to be CA stack - 3 gh AT (7) T where h is the height of the window [13]. The ideal velocity profile for bi-directional flow through a large opening is parabolic according to Bernoulli theory (see Figure 2c). Since this airflow profile varies significantly along the opening height, the airflow is integrated over the height, producing the 1/3 constant in this equation [13]. Appendix A.1 shows this equation's derivation. The value of Cd for bi-directional flow through a single opening should be adjusted from its standard value of 0.61 (for a sharp edged orifice) according to specific losses and boundary conditions. All viscous effects such as surface drag and interfacial mixing are included in this coefficient. For single-sided ventilation through a single opening, the effect of interfacial mixing causes some of the outgoing warm air to be entrained by the incoming cold air, reducing the net ventilation rate. In a study performed by Kiel and Wilson [14], the value of Cd was therefore found to vary with temperature difference across the opening due to this interfacial mixing. Full-scale experiments were performed and the results showed a correlation with this interzonal temperature difference. Cd = 0.40+0.0045AT (8) At large temperature or density differences, little interfacial mixing across the counterflow interface was observed. This was indicated by a steep gradient in temperature at the interface. However, at smaller temperature or density differences, an increased interfacial mixing was observed by a more gradual variation in temperature. The decrease in value of the discharge coefficient is therefore a direct result of increasing levels of interfacial mixing. This shows why Cd, for flow through a single opening, is a function of temperature, as shown in Equation 5 [14]. When solving the appropriate volume flow rate equation for V stack in the above discussion, the condition, AT, must be known. However, when this value is not known for a particular space, since a value for T is 14 not always available, the total heat load within the space, equation can then be applied Q Q, is alternatively used. An energy balance - p cp ATinletoutiet (9) where cp is the specific heat of air (-1000 J/kg.C), and ATinet-outiet is the difference in temperature between the air at the inlet opening and the air at the outlet opening. Note that to make this temperature terminology consistent with the previous temperature terminology (AT),ATinet.outiet is assumed to be twice the value of AT. This condition assumes a linear temperature profile within the space, which was found to be suitable. This assumption produces Q = 2p-cPAT (10) Note that since the terms, Y and AT, appear in both the semi-analytical calculations and the above energy balance equation, these equations must be solved simultaneously to obtain the correct temperature difference and volume flow rate. This process of solving the energy balance equation and the necessary volume flow rate equation simultaneously will also hold true when determining wind-driven and combined-driven ventilation rates. A difficulty in applying the above semi-analytical method is the significant variation of the temperature profile over the indoor height. This is a well-known problem, often solved by taking an average value for the indoor temperature, as the above equations have done, thereby neglecting temperature stratification and varying indoor air density. In order to address this problem, several complex models have been developed which more accurately represent the behavior of openings with temperature stratification. Li [12], for example, presents a model that assumes a piecewise constant temperature profile. Although more complex models similar to this one have been and are currently being developed, these analytical methods are still limited in their applicability, since they only apply to a narrow range of problems. 2.2.2 Network Models Network models are also used in calculating air velocity and estimating airflow rates, by applying pressure boundaries from Bernoulli theory to each building zone and opening. Some network models that have been developed are ESP [15], AIRNET [16], COMIS [17], NORMA [18], BREEZE [19], and PASSPORT-AIR [20]. These models combine the effects of wind and buoyancy to calculate pressure differences across nodes in the airflows between building zones and the outside environment. A depiction of a sample network model is shown in Figure 3. & pressu" node L flow path Figure 3: Sample of network modeling 191 15 However, these models have failed in the past to accurately predict the airflow rates in naturally ventilated buildings. This is attributed to the fact that turbulence, which plays an important role in natural ventilation, is not taken into account when modeling the airfbw. Network models consider the steady wind effects at an opening but neglect the turbulent effects and the corresponding fluctuating pressures, making these tools unsuitable for detailed analysis of natural ventilation design, especially singlesided ventilation. 2.3 Experimental Methods The physical mechanisms of single-sided ventilation have been studied through several experimental analyses in the literature. Wilson and Kiel [14] made measurements of buoyancy-driven flow through the exterior doorway of a test house using tracer gas experiments. When compared with a variable-density steady flow model, the results were in agreement. As part of this study, a correlation was made between inside/outside temperature difference and the corresponding discharge coefficient at the opening, as was shown in Equation 8. This relation was used within the current study, discussed in Chapter 4. Cockroft and Robertson [21] studied wind-driven ventilation through a single opening subjected to a turbulent impinging air stream, neglecting buoyancy effects. From this study, they derived simple theoretical wind models to predict this type of airflow. The model was then compared with experiments from a largescale model. The results from this study, however, only provided an indication of the magnitudes of airflows that wind may generate and concluded that further analysis and experiments were needed. Dascalaki et al. [22] also performed a wind-driven study, deriving the average airflow rate through the opening of singlesided natural ventilation configurations using tracer gas techniques. 2.3.1 EmpiricalModels Most of the experimental methods above have been applied to analyze the physical mechanisms of either buoyancy-driven or wind-driven flow through openings. Two particularly detailed studies analyzing the effects of both wind and temperature, separately and combined, have been performed. These two studies are discussed in the following paragraphs in detail and were carried out by: (1) British Standards Institution [23] (2) Phaff and deGids [24] These two studies have developed empirical models for single-sided ventilation. Most designers use empirical models to predict natural ventilation since these models offer a simple first estimation of the ventilation rate and mean velocity of a building, which are two important standards to evaluate the ventilation performance of a building. For cross ventilation due to wind and/or buoyancy effects, many models have been well developed and accepted and can take into account such parameters as wind direction, surrounding conditions, and window types [23, 25]. Although the existing single-sided ventilation empirical models (1 and 2 above) are not as widely accepted and are not as fully developed (e.g. neither model accounts for the impact of wind direction or window types on the ventilation rate), these simple models do provide a simple solution for determining the ventilation rates for singlesided ventilation. Since these studies have been the most developed in the field of single-sided ventilation, they are both considered in the current study, and discussed further in Chapter 4. The British Standards Code 5925 is a code of practice for natural ventilation design established by the British Standards Institution. In this standard, relationships for both wind and buoyancy-driven airflow through a large opening are developed. Ventilation rates for separate wind and stack effect, as well as a 16 combined wind and stack effect, which superimpose the effects of the two forces, are specified. The ventilation rates for stack, wind, and combined wind and stack flow through a large opening are given as Vstack Vwind C AC d 3out T gh AT (11, 12, 13) = 0.025AVocal Vtotal = V(Astack )2 ± ( wind )2 The stack term is identical to the well-established semi-analytical relationship given in Equation 7. The wind term is found in terms of local (site) wind speed values, Viocal. The experimental and analytical work performed by Phaff and deGids [24] is another detailed study considered in the current study, discussed in Chapter 4. Phaff and deGids performed experiments on the lowest-floor apartments of three buildings in different locations, using tracer gas techniques, to measure the influence of wind and buoyancy on ventilation rates through a large opening. Based on these experiments, they created an empirical model, which quantified the combined effects of wind, temperature, and turbulence. To represent natural ventilation provided in the absence of both wind and buoyancy, a constant turbulent term was added to the volume flow rate. This constant turbulence term is unique to this research study, as other studies on this subject make mention of only wind and buoyancy terms. The effect of turbulence was quantified by observed fluctuations in the air speed values. The resulting empirical model calculates an effective velocity, veff, through half the window opening, which is derived directly from the measured volume flow rate, * Ita g (Ap Veff -A 2 A /2 wind+ stack+ APturbulence) total. =CIVm +C2hAT + C3 (14) g where Vmet is the meteorological wind speed, h is the vertical height of the opening, C1 is a wind speed constant, C 2 is a buoyancy constant, and C 3 is a turbulence constant [24]. A reasonable correspondence between measured and calculated values was obtained for the fitting parameters, C1=0.001, C2=0.0035, and C 3=0.01 [24], yielding Veff - total =) .001-Vm +0.0035-hAT+0.01 A/2 (15) The resulting empirical model closely fit the experimental data. Note that this second study specifies wind-driven ventilation rates in terms of meteorological wind speed, while the British Standards study specifies this parameter in terms of local wind speed. Phaff and deGids used meteorological data instead of locally measured data in order to fit the data from the different experimental locations with a single correlation. The problem with this approach is that this empirical equation in only applicable to the environment density types (e.g. - city, urban, rural, country) of the experiment, which were given to be that of an urban environment. If the local wind speeds at a site are used instead of meteorological wind speeds, Equation 15 takes a more general form [26], Ve total A/2 - V0.0026V local 2+0.0035-hAT+0.01 17 (16) This equation can now be used with any specified environment density. These empirical results from the detailed experimental study were used for both validation and as a model for further analysis in the current single-sided ventilation study, documented in Chapter 4. Experimental methods used in determining airflow parameters usually use tracer gas techniques as a common way to study ventilation effectiveness. However, measurements of the air velocity have also been used in studies in order to derive the airflow rate through an opening. This technique has been successfully applied for measuring airflow through large internal openings [27]. However, for singlesided ventilation, the fluctuating nature of the wind produces continuously changing airflow patterns through an exterior opening. Therefore, a large number of simultaneous, highly accurate velocity measurements would be required to successfully predict the airflow rate for single-sided ventilation. This setup involves an experiment that is both difficult and expensive to perform. The tracer gas technique is therefore the preferred method in obtaining accurate airflow rates. The experimental methods mentioned in this section are critical to the understanding of singlesided ventilation, but can only deal with simple cases of flow since it is difficult to significantly change the design of an experimental setup. The value of the experimental method is therefore limited to the evaluation and analysis of existing structures. However, other methods, such as numerical modeling, are valuable in optimizing the various natural ventilation parameters prior to the building of a design. For these purposes, the experimental results serve as a means to evaluate the accuracy of the numerical calculations. 2.4 Computational Methods The value of the experimental method is limited to the evaluation and analysis of existingstructures, after the design and build process is complete. However, a second method, that of computational fluid dynamics (CFD) modeling, allows improvements to be made at the design stage. This is critical when deciding on optimum layouts and airflow fields for a particular building. It is also critical when considering costs - computational costs are decreasing while labor and material costs for experiments are increasing. It may be possible to optimize the indoor airflow distribution by changing the sie and position of openings and the shape of rooms for given outdoor wind conditions. Therefore, if used correctly, it is particularly useful and simple within CFD to predict the airflow distribution in a room by natural ventilation and to design the entire building layout in order to maximize the natural cooling resources available. CFD numerically solves the governing equations of fluid flow. These governing equations are derived by applying the principles of conservation of mass, momentum, and energy to a control volume of fluid. Because most indoor and outdoor airflows are turbulent, the CFD approach in this study uses turbulence modeling. Turbulence modeling links the unknown Reynolds-stresses to the mean flow variable through approximations. This type of turbulence modeling is called Reynolds-averaged Navier-Stokes (RANS) modeling. There are many turbulence models of this type used in CFD modeling. The model most commonly used is the "standard" k-g turbulence model, in which two equations for kinetic energy (k) and dissipation rate (F) of the model are solved. However, many modifications have been made to this model. In a study performed by Chen [28, 29], various indoor airflows were calculated with eight different turbulence models. From this study, it was concluded that the Re-normalization Group (RNG) k-g model performed best. This model is basically a variant of the k-E model, although computations are slightly more complicated and time-consuming than with the standard model. In this current study, a renormalization group (RNG) k-g model [30] was used. The flow-governing equations within CFD are highly non-linear and self-coupled, which makes it impossible to obtain exact analytical solutions to most 18 real cases. Therefore, CFD solves the equations by discretizing them through the use of finite volume techniques that convert the flow-governing equations to a set of numerically solvable algebraic equations. Although modeling turbulence through Reynolds-averaged Navier-Stokes (RANS) modeling is the most widely used CFD method in industrial applications, RANS encounters several difficulties when modeling building ventilation. First, RANS is not fully able to model transient conditions, such as those that exist for natural winds that vary with both speed and direction. When solving for a transient situation, RANS produces a quasi-steady solution that can be obtained at each time step. However whether these quasisteady results can represent a real transient condition is still in question, and is doubtful. Secondly, RANS modeling cannot correctly predict the airflow around buildings. This was confirmed when Lakehal and Rodi [31] compared the computed airflow results around a bluff body by using various RANS models. It was observed from the experiments of this study that most RANS models have difficulties generating the separation region on the roof, which was observed in the experiment. Furthermore, all of the RANS models overpredicted the recirculation region behind the body. This study also used a CFD method called Large Eddy Simulation (LES) in order to compare the results with the experimental data. The LES results agreed well with the experimental data, and are more accurate then RANS modeling. LES separates flow motions into large eddies and small eddies, through which LES computes the large eddies in a three dimensional and time dependent way, while modeling the small eddies with a subgrid-scale model. LES has been successfully applied to several airflows related to buildings and performs better than RANS modeling most of the time [32, 33]. However, LES requires far more computing time than RANS modeling and, therefore, cannot be practically used within the building industry, due to this heavy computational load. A typical calculation time for LES can be a week versus a few hours for RANS. This difference would have a major impact on the current single sided ventilation study in Chapter 4, which simulates a wide range of environmental conditions in order to evaluate trends and establish guidelines. The application of LES to such a task would be nearly impossible. For these reasons, it is important to evaluate within the current study whether RANS modeling for single-sided natural ventilation design is in fact feasible and capable of producing accurate results. The impact of such a study is valuable to the building industry in its move towards using practical tools to implement more energy efficient strategies such as natural ventilation. Several CFD studies have been performed on the airflow induced by single-sided ventilation, although far more studies have been performed on cross ventilation. Most of the single-sided ventilation studies focus on the effects of buoyancy-driven flow through a large opening. Schaelin et al. [34] used two- and threedimensional CFD to simulate the bi-directional wind and stack flow through a door opening by coupling the indoor airflow to the outdoor flow. Li and Teh [35] did a similar study on stack flow alone using a two-dimensional low-Reynolds-number turbulence model. They found that the airflow rate increased with the power of the heat source and height of the window. In this same study, they also studied the ventilation resulting from a mixed mode system. By introducing an air-conditioning unit into the space, cool indoor air was observed to flow out of the room through the lower part of the opening, while outdoor air was induced into the room through the upper part of the opening. The stronger indoor air mixing ventilation resulted in a lower airflow rate due to the reduction in vertical temperature gradient. The effectiveness of this type of mixed mode ventilation is an important issue, which will be addressed in the current study in Chapter 4. Another computational study was performed by Gan [36] on buoyancy-driven flow through a large opening in order to evaluate the effective depth of fresh air in a particular space. All these mentioned cases are purely numerical studies and do not incorporate comparisons with analytical or experimental results. Emphasis in these studies has been placed on evaluating a particular parameter, such as window height, heat source intensity, or effective depth of fresh air. These and other important design parameters were collectively considered in the current detailed single-sided ventilation study for both buoyancy and wind-driven flow in order to evaluate trends and produce general guidelines. The CFD models used in the current study are also compared with semi-analytical solutions, empirical models, and experimental results for validation purposes. 19 Some of the past CFD studies on single-sided ventilation perform coupled outdoor and indoor flow simulations, requiring an enlarged computational domain and grid size, while other studies assume the flow domain to be the indoor environment itself. When performing a CFD study, perhaps the most important consideration to be made is the selection of boundary conditions, which can have a major impact on the results of a particular study. Although a reduction in the computational domain size and time is desirable, it is more important to consider the accuracy of the results, which must not be compromised. The selection of appropriate boundary conditions plays a very significant role in the current study on single-sided ventilation. CFD modeling provides a valuable method for detailed airflow representation of more complex geometries and distribution of heat sources. A good representation of this principle can be seen in the different airflow patterns for the single-sided ventilation case in Figure 4. As the position of the same room is changed to a different floor, the flow pattern within the room is also changed. The whole-field results of CFD are therefore necessary in order to obtain a full understanding of the airflow within certain environments. This important aspect of CFD modeling is also illustrated in the current study.If CFD can be shown to produce accurate airflow results, it will be a very useful tool for single-sided natural ventilation design. 0 0 0 Figure 4: Airflow patterns in a single-sided ventilation room placed at different levels [371 2.5 Thermal Comfort and Indoor Air Quality In order to evaluate the effectiveness of a particular single-sided ventilation design, various parameters must be considered. These performance parameters are determined by the thermal and flow boundary conditions, such as size and geometry of a space, heat sources, and outdoor weather conditions. Some important parameters already considered have been indoor air temperature and airflow rate. These parameters can be combined with other influencing factors in evaluating two important parameters that are a part of the current study in Chapter 5: thermal comfort and effective depth of fresh air. These parameters are significant to the evaluation of natural ventilation since thermal comfort and indoor air quality (determined by the effective depth of fresh air) are the two major criteria that must be satisfied for an effective natural ventilation design. 20 Thermal comfort determines whether or not an indoor environment is satisfactory to the occupant. It is necessary to evaluate this parameter in natural ventilation design, especially since other parameters discussed so far, such as ventilation rate, cannot predict the level of comfort within a space. For instance, even at high ventilation rates, thermal comfort may present a problem. Thermal comfort indices, outlined in Appendix A.2 and A.3, are used in the design tool developed Chapter 5, to analyze the conditions for potential indoor environment designs. Using similar reasoning, the effective depth of fresh air must also be considered when designing for natural ventilation since locations of poor air quality within a space may not be determined just by ventilation rate and air temperature distribution alone. The effective depth of fresh air for single-sided ventilation is the distance that fresh air travels from the inlet into the space and is therefore a measure of the extent of fresh outdoor air penetration into single-sided naturally ventilated buildings. This important design parameter for single-sided natural ventilation is discussed further in Appendix A.4, which reviews a recent detailed study from the literature performed in this area. Overall guiding rules have been established in the literature for this effective depth of fresh air parameter with regard to single-sided ventilation and are shown in Figure 5 and Figure 6. These figures provide an upper limit to the allowable room depth for the two common opening geometries when designing for this strategy. W!5 2-5H h approxi 1-5 m H W Figure 5: Effective depth of fresh air for single-sided ventilation through an upper/lower opening 138] MI W 2H H I h7 W Figure 6: Effective depth of fresh air for single-sided ventilation through a single opening 1381 Compared with an upper and lower opening geometry, a single large opening generates lower ventilation rates and the ventilated air does not penetrate as far into the space. Single-sided ventilation is therefore effective to a depth of about: -> 2.5 times the floor to ceiling height for an upper/lower opening geometry (Figure 5) 21 2 times the floor to ceiling height for a single opening geometry (Figure 6) This effective depth is a measure of the extent of fresh outdoor air penetration into single-sided naturally ventilated buildings. Therefore, the room that is designed should not exceed this effective depth in order to maintain acceptable thermal comfort and good air quality. However, if this criterion cannot be met, ceiling fans or a similar type of mechanical assistance may be used to augment the effective depth of fresh air, allowing the space to be deeper if necessary. 2.6 Mixed-mode Single-sided Ventilation The previous sections have discussed issues pertaining to the natural ventilation of single-sided spaces in buildings. However, natural ventilation may not always be suitable for a particular climate or building. One option that is available to utilize natural ventilation within these situations is with the design of mixed-mode ventilation strategies. Therefore, natural ventilation can be combined with mechanical ventilation and/or air conditioning. Such combinations are known as mixed-mode ventilation systems. Mixed-mode ventilation strategies can be broadly categorized into three groups [38]: - - - Zonal mixed-mode (Figure 7): This involves a mixed ventilation system 'in space.' In other words, separate parts of a building that are used in different ways can be serviced differently from one another. Air conditioning can then be limited to only those parts of the building where it is necessary. Seasonal mixed-mode (Figure 8): This involves a mixed ventilation system 'in time.' In other words, both natural and mechanical ventilation systems are installed within a particular zone but are used at different times of the year. Usually, mechanical ventilation is run in winter and peak summer while natural ventilation is used in mid-season. Concurrent mixed-mode (Figure 9): This system provides mechanical and natural ventilation simultaneously. For example, in a very deep space where it is impossible for all occupied areas to be within the required distance of natural ventilation inlets or in a space exposed to external noise or sources of pollution, mechanical supply ventilation may be required with a natural exhaust. Mechanical supply can be provided through a displacement ventilation system, which ensures a good distribution of fresh air. The air that rises into the space can then be exhausted at a high level into a chimney or atrium. This type of system is analyzed as a mixed-mode option for the current study in Chapter 4. This type of system is very complicated to design, since special attention should be paid to the very likely occurrence of energy being wasted during the process. This can easily occur if excessive natural ventilation imposes an unnecessary cooling load on the mechanical system, or if cooled mechanical air escapes directly from the space without entering into and circulating through the occupied zone. 22 -71 Zone A Mechanical ventilation ) ( I Zone B Natural ventilation ) r--W~mtrWWA' Figure 7: Zonal mixed-mode strategy [38] Zone A Peak season (window closed, ( Zone B Mid-season (window open, mechanical ventilation OFF) mechanical ventilation ON) ) Figure 8: Seasonal mixed-mode system [381 23 External opening Floor mounted diffusers Figure 9: Concurrent mixed-mode system [381 The significance of mixed-mode ventilation applications is promising for future design. Since natural ventilation design is not feasible in many climates (e.g., hot and humid) and building types (e.g., offices with high internal heat loads), many designers are often left with no choice but to install mechanical ventilation and air-conditioning within the building. However, if the possibility to compromise with mixed-mode systems is developed and advanced further, applying these systems will be valuable in reducing the high-energy consumption costs that exist in the building sectors today and in creating a better, healthier, more sustainable indoor living environment. 2.7 Conclusions Natural ventilation is a critical strategy in the move towards energy efficient building design. In order for this strategy to be most effective, the interaction of natural and built forces must be determined. Singlesided ventilation is a significant type of natural ventilation, especially since singlesided building forms are so prevalent, especially in the US. It is therefore necessary that the physical behavior of this ventilation method be well understood. Unfortunately, single-sided ventilation has been given far less attention in the building research and design field than other forms of ventilation, such as cross ventilation. This is in part due to the fact that the effect of the natural forces of temperature and wind on the indoor environment is more difficult to determine, due to the lack of theoretical basis for the flow, making predictions of airflow difficult to correctly determine. Another area of uncertainty in this field is how the forces of temperature and wind interact when entering a space. This subject has received very little attention in the field. This chapter has compiled all the research and information on singlesided natural ventilation in the field of building technology today, in order to determine what is available and has been researched, and what are the areas where work still needs to be done. Many analytical, experimental, and numerical studies have been performed in the field of single-sided ventilation and help to provide information on the physical flow characteristics for this ventilation strategy. For buoyancy driven flow, well-established semi-analytical solutions have been developed to determine ventilation rates. For wind-driven flow, empirical models have been developed based on detailed experiments. These will be critical studies for comparison purposes with current findings. With his background of knowledge in the field of single-sided ventilation, it will now be possible to proceed forward in the further development of understanding this strategy. Research in the area of thermal comfort, indoor air quality, and alternatives to natural ventilation, such as mixed mode ventilation, will also be necessary to analyze the full potential of single-sided ventilation. This background information is significant in taking steps towards the improvement of natural ventilation design. 24 CHAPTER 3: CFD VALIDATION 3.1 Introduction Natural ventilation design is very complicated and must be analyzed in detail for optimum results. However, it is very difficult to achieve this goal, due to the variability of the outdoor environment. The conditions for natural ventilation cannot be controlled as in mechanical ventilation. Therefore, careful attention must be paid to natural forces, particularly those of wind and temperature. As was discussed previously, it is difficult to control and measure these unpredictable forces. A tool is needed that will enable designers to easily manipulate a building's design in order to observe trends and evaluate various potential designs. For these reasons, the potential for computational fluid dynamics (CFD) in the field of natural ventilation is very significant and needs to be addressed. However, at the same time, the uninformed use of this tool is even more detrimental, leading to misleading results on how natural ventilation forces impact a design. One necessary step of CFD modeling is therefore to validate the CFD model with physical results, in order to show that the predicted outcome is an accurate representation of the physical situation. Otherwise, even for simple cases, a model may predict inaccurate results that do not reflect the physical reality of the case. Therefore, for purposes of the current study, this chapter has been devoted to detailed validation cases for both indoor and outdoor flow. The first validation case is performed for an indoor mechanical displacement ventilation system. Although this case models mechanical rather than natural ventilation, the principles of single-sided ventilation are based on the physics of displacement ventilation. The ability to validate CFD techniques for the case of displacement ventilation strengthens the modeling case for indoor flow of single-sided natural ventilation in this study. After performing the indoor validation, a case involving flow around a cube is then validated in order to strengthen the current study's case with respect to modeling the outside domain. Finally, an experimental single-sided ventilation case is validated [42]. These three validation cases will aid in determining how strong a case can be made for the use of this computational modeling tool in the future design of naturally ventilated buildings. 3.2 CFD Indoor Validation -Displacement Ventilation This section presents the CFD results found from computing airflow in a space with mechanical displacement ventilation. The significance of validating a displacement ventilation case for a single-sided ventilation study lies in the fact that displacement ventilation and single-sided ventilation are based on the same physical principles of buoyancy-driven flow, as clearly shown in Figure 10. The flow characteristics of displacement ventilation - indoor temperature stratification and low air velocities - are normally found in single-sided natural ventilation. Air is generally brought into a displacement ventilated space through a diffuser located in the lower part of the room, just as outside air typically flows into a single-sided space through a lower window or the lower part of a window. Similarly, for displacement and single-sided natural ventilation, the air inside the space generally leaves through an exhaust or upper exterior opening, respectively, both usually located in the upper part of the room. The major force associated with both ventilation strategies is buoyancy, where heat sources create upward convective flows in the form of thermal plumes. Both displacement ventilation and single-sided natural ventilation take advantage of the naturally occurring thermal stratification in the room, removing heat and contaminants from the occupied zone and creating a better ventilation system. By determining whether or not CFD can accurately predict 25 flow and temperature fields for displacement ventilation, the validity of and confidence in simulating single-sided ventilation can therefore be partly determined. Exhaust Diffuser (a) A I11 Vj 11, A I (b) Figure 10: Physical principles of (a) displacement ventilation, and (b) single-sided ventilation [38] Arens [39] simulated detailed experiments of a displacement ventilation space, shown in Figure 11, simulating various industrial and office settings. The purpose of the experimental investigation was to evaluate the ventilation effectiveness of a particular displacement ventilation system, characterized by high ceilings and high heating loads. Testing the performance of high heating loads will carry over into the current single-sided ventilation study, which is also characterized by high heating loads. The experimental data collected for each displacement ventilation experiment [39] was used to validate the CFD model. A CFD model was validated for each experimental case, by comparing temperature and contaminant concentration measurements with computed values. The results from one such CFD case are presented in this study, while an additional case is provided in Appendix B. 3.2.1 Test Facility The experiments were conducted in a room equipped with both a high ceiling (6.5m) and a displacement ventilation system. The performance of the system was evaluated in the presence of a variety of modeled loads by use of appropriately placed temperature, tracer gas, and velocity measurements. The modeled loads consisted of persons, personal computers, and lighting loads found in offices, as well as simulators 26 constructed to represent generic welding, engine exhaust, and control panel enclosures in a manufacturing environment. Wall, floor, and ceiling temperatures were measured in these experiments. The resulting data was used to judge the suitability of displacement ventilation for a particular process setup within a building. The space studied, shown in Figure 11, is a conference room belonging to MIT's Urban Planning Group under the Department of Architecture. The displacement ventilation system was set to provide the room with roughly a constant airflow rate of 3 ACH throughout the duration of each test. The supply air is delivered from two opposing diffusers, located along the wall at floor level, while a single exhaust grill is located in the upper part of the room on the right-hand side of the layout (Figure 1 Ia), at a height of 5.0 m. The room is 6.5 m high. Three rows of fluorescent lighting fixtures are located 3.8 m above the floor and run east to west. Two large sound-absorbing ceiling panels are suspended from the room's ceiling and are located at 4.0 m above the floor. The room's exhaust is therefore located in the space between the panels and the ceiling. Due to limitations in access to this upper part of the test room, the analysis for the space focused on the region at or below the level of the suspended ceiling. A large area of the east wall is taken up by two very large sliding doors. Each door measures 2.1 m W x 4 m H and does not seal tightly with the room. The outline of each door is shown in Figure 1 b with dashed lines. Gaps in the range of 2 cm were found along the top and along either side of the door, which presented slight infiltration problems. 27 (outline of) OVERHEAD CEILING PANELS(3.7 m x 1.8m) :2.5m EXHAUST -(33 cmx33cm) -- .8 ---- --- - 0.3m 5m C I-bF 3.25 mn SUPP Y DIFFUSERS (127 cmiH x 64 cm W) 0.9 m (Front of Room) 0.3 m (THIS SPACE IS DEDICATED FOR INSULATED BUILDING UTILITIES AND DUCTWORK) EXHAUST GRILLE CEILING PANELS FLUORESCENT LIGHTING TEMP. SENSOR - a6.5 5.0 M SUPPLY DIFFUSER BLINDS COVERING WINDOWS ON FAR 3.8 I WEST WALL 6.5 m Figure 11: (a) Test room layout and (b) front elevation [39] 3.2.2 General ExperimentalSetup The types of cases tested in the experiments were those most typically found in high-ceiling spaces in the US. Several major parameters, such as floor area, room height, air supply volume, and lighting load, remained fixed. The values for these parameters are shown in Table 1. Given the test facility's limitations, two distinct types of high-ceiling facilities were appropriate for modeling: office environments and factory environments. From these two indoor environment types, a total of eight design setups were tested. The results from simulating one of these such cases in CFD is presented in the following section as a means for indoor airflow validation, while an additional case is provided in Appendix B. 28 Table 1: Experimental fixed parameters 139] Parameter Value Description Afoor 31.6 m 2 Floor Area 6.5 m Total Room Height 656 m /hr (approximately) Air Supply Volume 732 W Energy Load from Lighting to Space H s, 3 Qlighting For each experiment, temperature, velocity, and concentration measurements were taken with thermocouples, an anemometer, and tracer gas circuits, respectively, using a vertical telescoping pole. This pole had nine thermocouples and seven tracer gas circuits mounted at different elevations. In addition, a single hot-sphere anemometer was mounted and could be moved by remote control to any height along the pole to acquire velocity data. A full set of these measurements was taken at each of ten positions indicated during each test. In addition, temperature and tracer gas measurements were also taken at the north supply diffuser and at the exhaust grill. Surface temperature measurements were also taken along the walls and floor, as well as at the surface of each heat source (with the exception of light sources and extremely high heat sources). Conditions were allowed to stabilize for a minimum of four hours before any data was collected. Heat sources for the various experiments included occupants, computers, and equipment. A box containing incandescent light bulbs with appropriate wattages was used to model each heat source. For those particular heat sources modeled as contaminant concentration sources, tracer-gas sources of SF 6 (1% by volume) were injected from the top of each appropriate heat source at a rate of 863 standard cubic centimeters per minute (sccm). The hot-sphere anemometer used in the experiments was not able to give good results for magnitudes below 0.08 m/s due to unreliable calibration below this value. Limitations were therefore encountered with the air velocity measurements taken. The anemometer was also used to measure the air volume flow rate delivered by the supply diffusers. The room was provided with roughly a constant air volume flow rate of 3 ACH throughout the duration of each test. While this ensured that the air volume flow rate was constant over the course of the experiment, a covering of thin, tightly-woven material placed over each diffuser ensured a uniform air volume rate over the area of the diffuser itself. Air velocity measurements, taken in a grid pattern over the face of each diffuser and added to determine the total airflow rate, verified this constant flow rate. 3.2.3 General CFD Setup Using the experimental setup information, the displacement ventilation space was modeled in CFD, shown in Figure 12. After the space was set up, each of the experimental cases, with relevant heat sources and boundary conditions, was simulated in CFD and compared with the experimental results. When finally comparing computational modeling results with those of the experiment, the conditions along the height of the various probe positions were analyzed. In order to model the physical environment of the displacement ventilation space, certain assumptions were made within CFD. These general assumptions were: * Surface temperature measurements, rather than heat flux values, were used for boundary conditions when setting up the CFD model. This produced more accurate results. Only when temperature measurements were not taken (e.g. light fixtures, hot plate) were heat fluxes then used as boundary conditions in the CFD program. 29 . . For temperature boundaries, each surface was modeled with a specific film coefficient, h,, and temperature value. The two floor-level diffusers were modeled as inlets with specified ventilation rates and temperatures (see Table 2). . . . The ceiling level, located at a height of 6.5 m, was actually modeled as being at the height of the return exhaust, which was located at 5 m. Setting the ceiling and return exhaust locations at their different heights would have created difficulties in the computational modeling of this situation. In the experiment, the space between the two heights is assumed to be a fully mixed zone, which makes this assumption more valid. A fine grid was generated for each case. The maximum grid density capable of being run on the computer for the various cases was approximately a 72 x 52 x 52 grid. This fine grid was used to validate the model for each case. To model turbulence, the RNG k-6 model was used. Table 2: Inlet flowrates and temperatures [39] Case 1 2 Description Light Welding Shop Cubicle Office (Appendix B) Total Heat Load (W) Ventilation (m3/hr)Rate (OC) 1854(57 W/m2) 1392(43W/M2) 703.6 652.7 15.50 15.43 si Figure 12: CFD setup of displacement ventilation space 30 3.2.4 Light Welding Shop Case - Experimental and CFD Results The type of case chosen for validation was a factory environment type. The specific case modeled was a light welding shop case. This welding shop case modeled high temperature heat sources that might be found in a welding operation setting. This involved the simulation of one person, one computer, one control panel, and a hot plate (representative of a small, hot, highly convective metal surface undergoing welding). The heat loads and surface temperatures for these sources are shown in Table 3. This experimental layout and CFD setup are shown in Figure 13 and Figure 14, respectively. A tracer-gas source was introduced from the top surface of the welding simulator, labeled W. The ten measuring locations designated in Figure 13 are: Si, S2, W1, W2, N1, N2, N3, E1, E2, and C. Table 3: Heat sources for light welding shop case [39] Load ID P1 Description Person Simulator Heat Load (W) 95 Surface T ('C) 29.1 El Control Panel 396 34.1 CI W PC Simulator Welding Simulator Lighting 171 460 732 42.3 -- --- N -I I * WI El *S1 W2 *S2 *C *N3 * N2 *N1 Tracer Gas (center of room) . E2 *El TABLE (Front of Room) Figure 13: Experimental setup of light welding shop case [391 31 Figure 14: CFD setup of light welding shop case The CFD program was validated by comparing the temperature (Figure 15) and concentration (Figure 16) values from the measured data with the computed results. Since the hot-sphere anemometer used in the experiment was not able to produce results for velocity magnitudes below 0.08 m/s, and the airflow through most of the space was below this velocity, comparisons of velocity could not be made. Each graph represents one of the ten measurement locations throughout the room. In Figure 15, the agreement between the temperature measurements and computational predictions is excellent. In Figure 16, the concentration measurements and computations also agree very well with each other, with just a few discrepancies in the upper part of the space where computational results overestimated the concentration of SF6 . The tracer gas source was introduced from directly above the welding simulator or hot plate. For the displacement ventilation system t> work effectively, this stratification layer should be above the breathing zone of a standing occupant in the space. It is clear from Figure 16 that the stratification occurs well above the occupied breathing zone and is therefore effective. Since the tracer gas source was a point source for this experimental case, the concentration values are very sensitive to location. Also, there was found to be a slight mass imbalance in each of the experimental cases due to infiltration through the east sliding doors. This infiltration would result in a dilution of the SF 6 tracer gas concentrations throughout the room, producing lower concentration values than that of a completely sealed room. Overall, however, the tracer gas measurements and calculations were found to agree well with each other. 3.2.5 Conclusions From the detailed experimental displacement ventilation study performed, CFD techniques were used in order to validate these experimental results. Computational models were set up and simulations were 32 performed for factory type and office type cases. The results from a typical factory case are shown and discussed in this section. Experimental measurements of air velocity, air temperature, and tracer gas concentrations were taken at various locations throughout the room. However, since anemometer limitations prevented accurate air velocity measurements from being made at low air velocities, comparisons of this parameter could not be made. Temperature and concentrations values were compared for a light welding shop case. The air temperature calculations agreed well with the measured data. However, some discrepancies were found between the calculated and measured tracer gas concentration, although the overall patterns and values were very similar. Despite these discrepancies, CFD is found to be a valid tool in simulating the indoor airflow for displacement ventilation, a strategy upon which singlesided ventilation principles are based. 33 2 (m) 2(m) -i CD - in Li) 0 N W - 01 Q 8N Z (m) Or'.) in r'.) CD PO co) 2(m) ~ ) -4 01 Q ON 2(m) (m) Z (M0 -4) ON 002 N (M) - ~ z 01 O -4 2(m) CD 2 (in) NI> (M 1 CN S 4. ON) 0D N, Cl 4. 04 Or Figure 15: Comparison of experimental and computed temperature profile for light welding shop case 34 2(m) Z(m) -&I (M a) (j) Z (M) 2(m) Z( ) Of 33 3 ro - N.) 2 Z (M) 2(m) CD 2 2, 63 CD 2(m) -1 - m 33N Z2(m) (in) 41 2(m.. ) ........ ............ ........ ............ ro> CD CD -001 '1D, 33 ........ ....... ....... R; .4D ....... 2 (Z) 4. P1 0D Figure 16: Comparison of experimental and computed SF 6 concentration for light welding shop case 35 CFD Outdoor Validation -Flow Around a Cube 3.3 Full-scale tests, wind tunnel tests, and computational techniques are common procedures in studying the building and its surrounding outdoor environment. The full-scale test and wind tunnel test are usually time-consuming, expensive, and also may not be capable of capturing whole field information, since there can only be a limited number of measuring points. The development of CFD allows for the investigation of building wind environments, enabling the study of entire detailed flow fields in a timely and cost effective manner. In order to utilize such a powerful tool, it is necessary to validate the CFD model developed with existing experimental data. Once a validation can be made, the use of the model can then be extended to a variety of conditions that may or may not have been tested experimentally. This is a great advantage to using CFD techniques in order to solve building environment problems. Natural ventilation studies require information of both indoor and outdoor airflows, which are significantly different. The need to validate the CFD modeling of the outdoor environment for natural ventilation is as significant as validating the indoor environment, if not more so. A model that can simulate both outdoor and indoor airflows successfully can be used to study natural ventilation. The following section studies flow around a bluff body to determine the performance of CFD in modeling outdoor flow. 3.3.1 Experimental and CFD Setup The ability to accurately model outdoor airflow around buildings is necessary to provile the correct boundary conditions for the indoor building environment that is naturally ventilated. The experimental case that was chosen as a validation case for CFD was the measurement of pressure coefficient distributions, C,, along a block. The Architecture Institute of Japan (AIJ) working group performed this experiment in a wind tunnel by applying a wind velocity profile of zV4 to a 2H x 2H x 1H block [40]. The measurements of pressure coefficients were taken along the section centerline and vertical centerline of the block. These measurements were used for validation purposes in this CFD study. Wind passing around a building creates surface pressures, which depend on the speed of the approaching wind. These surface pressures on a building surface may be defined in terms of a pressure coefficient, Cp, given by [41] C P = I -pV (17) 2 2 where po is the reference pressure at free flow, and V is the approach velocity at the building height. The surface pressure, p, is relative to the reference pressure located away from any influence of buildings. When referring to Equation 17, C values are positive along stagnation regions, where surface pressures are higher than upstream reference pressures. C values are negative along separated flow regions on the roof, sides, and rear of a building, where surface pressures are less than upstream reference pressures. This distribution of C along the surface of a bluff body was measured in the experiments by AIJ and compared with the results from a CFD model. A CFD model of this flow around a bluff body was set up according to the experimental wind tunnel case, and is shown schematically in Figure 17. The wind velocity profile of z 14 was represented by a series of inlets of incremental height stacked in the vertical direction, upstream of the block. After performing this 36 simulation, the calculated pressures along the block surface were extracted (p), while a value for po and V was obtained in the upstream flow, away from the block. 6H z y -1OH -H 0 H (a) 20H -1 OH -H y inlet outlet H X 1OH I (b) Figure 17: Experimental and CFD setup for flow around a bluff body: (a) section view and (b) plan view 3.3.2 Experimental and CFD Results The pressure coefficient results were extracted along the centerline of the block in the lateral and vertical directions. The results for C, distributions along these two planes are shown in Figure 18. After comparing the C, results from the experiment and the CFD calculation, the agreement between the two results was found to be very good overall. One location where the agreement was not as close was on the top of the block, where the CFD calculation underpredicted this separation region. As explained in Section 2.4, Lakehal and Rodi found in their study that RANS models have difficulties generating the separation region on the roof, which was observed in the experimental part of their study [31]. It has therefore been found in past research studies that this phenomenon is common when using RANS models. CFD predicted the pressure coefficients along the center height of the block very well. For the section plane comparisons, CFD did overpredict several C, values in the front of the block, but to a small extent. 37 -1.5 - -1 0~ C -0.5 - 0 y 1.5 1 0.5 0 Experiment + Cp 0 CFD] -0.5 -1 -1.5 Cp (a) -1.5 - -1 1 Cp -0.5 0- 10y . 1.5 1 Cp . . 0.5 ,1 0 -0.5 -1 -1.5 Cp -0.5 - -1 - Cp -1.5 J + -CFD Experiment (b) Figure 18: Comparison of experimental and computational distributions of pressure coefficients, C , around a block: (a) center section and (b) center height of the block 38 3.3.3 Conclusions The surface pressure distributions along a bluff body subjected to oncoming wind were studied to ensure that CFD could accurately model outdoor airflow, a significant task when defining the boundary conditions for an indoor naturally ventilated space. The experimental and CFD results were found to be in agreement. Although CFD did underpredict the recirculation region on the top of the block, the discrepancies in this localized area are not anticipated to have a large impact on the current natural ventilation study. 3.4 CFD Validation of Single-sided Ventilation The final step in this CFD validation process was to validate a single-sided ventilation case in order to prove the validity of and gain more confidence in the method used to model the cases studied in Chapter 4. In this validation study, CFD has been used to analyze single-sided ventilation by studying wind-driven flow through a large opening. A single-sided ventilation experiment was used to validate the CFD model [42]. 3.4.1 Wind-driven Single-sided Ventilation Experiment Wind-driven single-sided ventilation experiments were performed in a wind tunnel at Cardiff University for the purpose of comparing the results with large eddy simulation (LES) tools [42]. These experiments studied both cross ventilation and single-sided ventilation. The velocity distributions around and inside the building were measured, and have been used here to validate CFD modeling of wind-driven singlesided ventilation. The wind tunnel at Cardiff University consists of a 2m x 2m working section that is Im in height. A onedimensional Laser Doppler Anemometer (LDA) was used to measure the velocity distributions around and inside the building models. The velocity measurements were taken along the center section of the building, and both mean and root mean square (rms) velocities were measured. The mean velocity measurements were used as a comparison for this CFD validation. Since LDA is a one-dimensional system, the velocities along the streamwise (y) and vertical (z) directions were measured separately. The velocities were measured along 10 vertical lines, shown in Figure 19, and there were 18 measuring points along each vertical line, ranging from 25 mm to 500 mm high. The incoming wind speed at the top of the vertical profile was 10 m/s. H H/25 -H/25 H =250 mnm z HA 4 -3H -H -H/2 0 311/4 H/2 H Figure 19: The line locations of velocity measurements [42] 39 H+H/2 H+4H A schematic view of the building model used for single-sided ventilation is shown in Figure 20. The dimensions of the model were 250 mm x 250 mm x 250 mm, with an opening in the windward wall measuring 84 mm wide x 125 mm high. The thickness of the walls was 6 mm. z .......................... .............. .............. ............... 125 ...... .......... 250 ......... ... ........ 83 ; 8 .......... .......... ::83 ..................... ........... ........... 250 Wind Unit: mm Figure 20: A schematic view of the experimental building model for wind-driven single-sided ventilation [421 3.4.2 Wind-driven Single-sided Ventilation CFD Model For the CFD simulation, the building model was set up up and placed within a larger computational domain. The outer computational domain had an upstream length of 4H, a downstream length of 8H, a lateral length of 4H on both sides of the building, and a vertical length of 3H above the building height. This model is shown in Figure 21. 3H Figure 21: Computational domain for CFD building model 40 3.4.3 Experimental and CFD Results After setting up the CFD model according to the experimental setup, the simulation was performed. Figure 22a and b show the velocity field results for both the experiment and the CFD model, respectively, at the center section of the building. The overall flow patterns for both cases are similar, especially the windward velocity field, which shows a large reverse flow along the ground in both cases. However, the windward velocity field seems to agree much better than the leeward velocity field. In the leeward region, CFD predicts a larger recirculation zone than exists in the experimental results. The details of how these flow patterns differ around and inside this building model become quite clear when next comparing the velocity profiles at the 10 streamwise locations. -~- ~. -~- recirculation zone -~ -~ -~ (a) recircuiarion zone Z fE 4~ --- i (b) Figure 22: Mean velocity vector fields at the center section: (a) experimental 1421 and (b) CFD results The velocity, v, was measured at 10 locations along the streamwise (y) direction, all at the center section of the building. These measurements were compared with the CFD results for the v velocity fields. The results are shown in Figure 23. The overall agreement between the CFD predictions and the experimental results is very good. The calculations for windward velocities and the velocities within the building model are very similar to that of the experiment, and are therefore found to validate the experiment well in these regions. On the leeward side, however, CFD tends to overpredict the recirculation region, which has been confirmed to occur in previous literature studies [31]. The problems encountered with predicting the 41 leeward velocity field for RANS modeling in CFD were mentioned and shown earlier, and will have an impact on predicting single-sided ventilation for leeward openings in a building. The velocity, w, was also measured at 10 locations along the streamwise direction, all at the center section of the building. These measurements were compared with the CFD results for the w velocity field. The results are shown in Figure 24. The overall agreement between the CFD predictions and experiment is very good and similar to that of the v velocity comparisons. On the windward side, these velocity results are good, with the exception of y=H-H/25. It should be noted, that for this point, LES results, from the same study that performed the experiments [42], also produced this similar low velocity profile near the ground. This may suggest sources of error in the experimental measurements at this location, especially since LES was found to perform very well overall in the aforementioned study and for outdoor flow modeling in general. Again, the w distribution on the leeward side of the building model was found to be higher in CFD, verifying the tendencies in RANS modeling to owrpredict this recirculation region. 42 Y=-H/25 Y=-HV2 Y=-H Y=-3H 0.5 0.5 0.5 0.4 0.4 0.4 0.3 0.3 0.3 0.3 N * 0.5 5 0.4 N N 0.2 0.2 02 0.2 0.1I 0.1 0 0.1 N 0 -0.4 0 04 VIref 0.8 -0.4 12 0 V/Vref 0.8 12 -0.4 0 V/Vref 0.8 -0.4 1.2 0.3 0.5 0.4j 0.4. 0.3 0.3 0.2 02 0.2 0.1 0.1 01 01 -0.4 V 0 0.4 V/Vref 0.8 1.2 N +N 02 0 0 Y=H+H/25 0.5 0.5 0.3 0.4 Y=3H/4 Y=H 2 Y=H/4 0.5 N 04 0.4 VIVref 0 0 . 0.8 12 -0.4 0 0.4 V/Vref 0.8 -0.4 12 04 VIref 12 0.8 -0.4 0 04 VNref 0.8 1.2 Y=2H Y=H+H/2 0.5 0.5. 0.4 0.4 0.3 0.3 N 0.2 N * Experiment ___CFD 0.2 01 0.1 0 -0.4 0 2 0 0.4 VIref 0.8 1.2 -0.4 4 0 V/Yr ef 8 12 Figure 23: Comparison of experimental 1421 and CFD results: v-component (streamwise) velocity distribution at 10 streamwise measurement locations; vref=10 m/s, Y<0 windward outside, 0<Y<H inside, Y>H leeward outside 43 Y=-H Y=-3H Y=-H/25 Y=-V2 0.5 0.5 0.5 0.5 0.4 0.4 0 .4 0.4 0.3 0.3 0.3. 0.3 N N N 0.2 N 0.2 0.2 0.2 0.1 0.1 0.1 0.1 04 01 0 -0.4 n 0 0.4 W/Wref -04 0----- 0 W/Wref W/Wref -0.4 0.5- 0.5 0.5 0.4 0.4 0.4 - 0.4 0.3 0.3 0.3 0.3 N N 0.2 0.2 0.2 N 0.2 0 -0.4 04 W/Wref 0. -04 0.1 0.1 0 11 0 04 W/WA&ef 0.4 0.4 0.3 0.3 N 0.2 N 0.2 0.1 0.1 0. 0 0 0 W/Wref -0.4 0.4 0 WI~ref Y=2H 0.5 WIWref 0 -- -0W4 Y=H4+H/2 0.5 -0.4 0.8 0.5 N 0.1 &/Wre4 Y=H+H/25 Y=3H/4 Y=H/2 Y=H/4 0.4 0.4 3 + ~~~ Experiment OFD 4$ -0.4 0 W/Wref 0.4 Figure 24: Comparison of experimental 1421 and CFD results: w-component (vertical) velocity distribution at 10 streamwise measurement locations; v ref= 1 0 m/s, Y<0 windward outside, 0<Y<H inside, Y>H leeward outside 44 0.4 3.4.4 Conclusions From this validation case, it is clear that the agreement between experimental results and CFD modeling for the interaction between outdoor and indoor flow in single-sided ventilation is very good. The strength of the CFD tool for this case is in the accurate simulation of windward and indoor flow. Leeward flow presented problems in this CFD validation case and could therefore not be fully validated. These difficulties must therefore be noted and taken into consideration when studying single-sided ventilation in the leeward region of a building. 3.5 Conclusions CFD modeling is a necessary tool in natural ventilation design. It enables designers to analyze different designs and evaluate the abilities of these designs before beginning actual implementation of them. However, since CFD has the capabilities of being a very powerful tool in this respect, it is also very important therefore to ensure that it is applied accurately. This is especially true for the case of natural ventilation, which is characterized by unpredictable and complicated airflow patterns and presents a challenge to the field of CFD modeling. Therefore, in this chapter, the CFD tool has been validated solely for the purpose of natural ventilation studies. The performance of CFD for these validation cases has been very good and promising overall. For indoor flow, CFD was able to accurately predict air temperature and concentration distributions throughout a room with mechanical displacement ventilation. Verifying the temperature and concentration fields for such an environment, although it is mechanically ventilated and not naturally ventilated, is very significant because displacement ventilation and single-sided ventilation are based on the same physical buoyancy and airflow principles. When performing a CFD validation on outdoor airflow around a bluff body, the pressure coefficient results from CFD were found to agree well with the experimental measurements. CFD was shown, however, to underpredict the separation region on top of the block, which is not believed to impact its intended applications towards single-sided ventilation. A similar validation was then performed, which included the indoor and outdoor environment for single-sided ventilation. For this case, velocity distributions were compared along the streamwise direction of flow. An excellent agreement was found in velocity distributions along the windward and indoor sections of the building model. However, the computational results for the leeward velocity distributions did not agree well with the experimental data. This inability of CFD to accurately model the recirculation zone on the leeward section of a building will therefore have an impact on the study of single-sided natural ventilation in this location. 45 CHAPTER 4: SINGLE-SIDED VENTILATION STUDY 4.1 Introduction From the previous chapter, it is clear that CFD is a powerful tool and can provide great potential for the future design of naturally ventilated buildings. The behavior of simulated airflow for both indoor and outdoor environments has proven to be representative of the actual physical situation for a majority of cases. Based on the validation of separate ventilation cases for both indoor and outdoor airflow, along with validation of a single-sided ventilation case accounting for the indoor and outdoor environment, the case for computational modeling of single-sided natural ventilation is strongly supported. CFD modeling, along with theoretical, semi-analytical, and experimental models, will be utilized in this chapter to create an overall, in-depth study and analysis of single-sided natural ventilation. This study was simplified to the analysis of a single, typical case, focusing on an innovative student residence building being designed by Steven Holl Architects for the Massachusetts Institute of Technology (MIT) [43]. The single student residential units within this building were initially designed with the intenton of single-sided natural ventilation, and are therefore the concentration of the study. The evaluation of several ventilation design revisions over the course of this proposed building design have also been beneficial in allowing for further analysis in this study. This ongoing process provided the opportunity to explore various design options related to single-sided ventilation. From this base case analysis, trends were then developed and extended to any indoor and outdoor environment in order to develop tools that allow designers to account for this ventilation strategy in their own individual designs. 4.2 Building Design A 350-student residence building (shown in Figure 25a), designed by Steven Holl Architects, has been designed for the Massachusetts Institute of Technology (MIT) campus, in Cambridge, MA, with a design concept of "porosity" [43]. It is ten stories tall and 330 feet (101 m) long. The porous building morphology presents a "sponge" concept for the new undergraduate residence hall. The overall building has five large-scale openings. These roughly correspond to main entrances, view corridors, and the main outdoor activity terraces of the dormitory connected to large spaces, such as the gymnasium. Vertical porosity is created in the block with large, dynamic openings, referred to as the "lungs" of the building, bringing natural light down and moving air up through the section. This building is an appropriate basis for the current study because it incorporates the natural environment throughout the building. The focus of the present study is on the single student rooms, which have nine operable windows measuring 2.2 feet W x 2.2 feet H (0.66 m x 0.66 m) in size, or 0.44 m2 in area, which greatly contributes to the concept of porosity (see Figure 25b). Although the window to wall ratio seen in the figure is unusually large, the effective opening area for each of the nine windows is actually only 0.13 ni. An 18inch (0.457 m) deep wall naturally shades out the summer sun, while allowing the low angled winter sun in to help heat the building. The layout of these single rooms, with a bed, desk, closet, and bookcase, is shown in Figure 25b. This space will be the focus of the current single-sided ventilation study. 46 (a) (b) Figure 25: Student MIT residence building designed by Steven Holl Architects [431: (a) building layout (b) single student room layout 4.3 Student Residence Room -General CFD Setup The CFD method was used to evaluate single-sided ventilation for a single room (2.9 m x 4.7 m x 2.8 m) within the student residence. The general room model that will be used throughout the current study is shown in Figure 26. The heat sources in the room consist of a computer (300 W), television (300 W), and one occupant (100 W). This total of 700 W was chosen based on what the designer assumed to be a typical heat load for this student space. This heat input includes both convective and radiative components; each comprises approximately half of the total heat. The surrounding walls, ceiling, and floor absorbed the radiative heat component, while each heat source was modeled as a convective heat component. (See Appendix A.5 for detailed calculation). The total heat load handled by a natural ventilation system is obtained by adding solar gains to these internally generated heat gains. However, for purposes of the current time-averaged ventilation study, solar gains were not considered. Although the window design for each student room consists of a 9-window grid (see Figure 25b), this investigation simplified it to allow for a more general single-sided ventilation study. The net open area of the 3 upper and lower windows was used to create one upper and lower window (0.4 m 2 each) in the CFD model, as shown in Figure 26. In order to also address the single opening geometry trends for single-sided ventilation, another part of the investigation focused on analyzing single-sided ventilation through a single 0.65m 2 window. A window of this dimension (rather than a 0.8 m 2 opening, which would be equal to the total upper and lower opening size and therefore comparable) was chosen for this study because an empirical model that has been developed for single openings was based on a window of this average size and this model will be compared with CFD results later on in the study. When modeling temperature, the outdoor air temperature is maintained constant at 25.5 0 C,the average noon temperature for Boston in July [44]. The intention is to analyze the results for this fixed outdoor temperature, and then to apply these results to a range of outdoor temperature conditions to develop trends. 47 0.66 m 0.6 m PE N Figure 26: Indoor stack model for single-sided ventilation study in CFD 4.4 Thermal Buoyancy Study CFD analysis was first performed for buoyancy-driven single-sided ventilation without wind. Simulations were run for both an indoor and combined indoor and outdoor environment to determine appropriate boundary conditions. A comparison was then made between the two models and the semi-analytical equations for buoyancy-driven flow in order to determine how the CFD models perform for this temperature-driven force. 4.4.1 Indoor stack model In order to set up a single-sided ventilation case in CFD, it is necessary to make certain assumptions and simplifications to the geometry in order to find a solution. One assumption initially made pertained to the boundary conditions at the ventilation openings of the room. For the indoor stack model, shown in Figure 26, the upper and lower windows were modeled as outlets at zero pressure and zero gradients for other variables, such as velocity and temperature. Assuming a zero pressure at each implies that the outside hydrostatic pressure was neglected. From this model, the airflow and temperature fields were derived. The CFD simulation seemed to produce reasonable buoyancy-driven airflow patterns, with colder air entering the room at the lower opening and warmer air exiting the room at the upper opening, as shown in Figure 27. The temperature field results in the center section of the room, shown in Figure 28, also exhibited typical stratification characteristics for this form of ventilation. To determine the validity of this indoor model, the outdoor environment was included in a combined model. A comparison was then made between the two CFD models and the semi-analytical equations for buoyancy-driven flow. 48 PEFFIF-_ V= 0.1 Ms X, , , / E~~ -- -- - - -- -- - E ~ ~ -E-E -t- -E E -E -ii 6i.- Figure 27: CFD results for indoor stack model in the center section of the room: velocity vectors (m/s) 3.0 32.9 32.5 32.5 _______________-32 -30.8 __5 30.8 2. -29.5 27.6 26.8 Figure 28: CFD results for indoor stack model in the center section of the room: temperature contours (C) 4.4.2 Combined indoor and outdoor stack model Since the vertical (hydrostatic) pressure distribution plays a significant role in buoyancy-driven flow, the combined indoor and outdoor stack model included the outdoor environment as well. In this model, three identical student rooms were stacked vertically above one another to evaluate the effect along a building's height. This three-story setup was placed within a larger outside domain (see Figure 29). After several simulations, a minimum dimension for the outer domain was determined (6 m x 10 m x 12 m), for which the results were found to be independent of domain size. Although this combined model for buoyancydriven flow necessitates more computational time and effort, it still requires a smaller computational 49 domain than a typical wind-driven flow study. However, convergence for buoyancy problems typically takes five to ten times longer than that for wind problems [45]. This further supports the need to minimize the computational domain of the stack model. CFD is particularly sensitive to boundary conditions for buoyancy-driven flow. Unrealistically high airflows and unreasonable pressure distributions were found for the combined model when zero pressure boundary conditions were defined for the side and upper boundaries. Therefore, the present study used the following boundary conditions: * Side Boundaries:solid plates with slip boundaries and a temperature equal to the outdoor air. * Upper Boundary: zero-pressure boundary at the outdoor air temperature. * Lower Boundary: solid adiabatic plate with non-slip boundary. Figure 29: Combined indoor and outdoor stack model for single-sided ventilation study in CFD After the combined indoor and outdoor stack model was set up, this model was simulated to produce airflow and temperature field results. The velocity airflow field resulted in buoyancydriven flow patterns similar to those of the indoor model. This airflow pattern is shown for the combined model inFigure 30. However, the magnitude of the overall velocity field was higher than that of the indoor model, as is indicated by the reference velocity vector at the upper right-hand corner of Figure 30 and Figure 27, respectively. Temperature field results, shown in Figure 31 a, produced a vertical stratification typical of buoyancy-driven flow. However, the magnitudes for temperature also differed from that of the indoor model, with the combined model producing lower overall temperature results. In addition to providing velocity and temperature results, the combined stack nndel also provided information on the relationship between indoor temperature and vertical location of the space. Although the spaces were physically and thermally isolated from one another, the temperatures in each space 50 increased with height due to the outside thermal plume from the openings underneath, as shown inFigure 3 Ia. This can clearly be seen from shifts in the graph of indoor temperature versus height shown in Figure 3 1b. This type of effect seems feasible for this case due to the small distance between upper openings of one space and lower openings of the above space. This may therefore need to be a design consideration, perhaps alleviated by staggering the grid of windows on the building facade. In the following section, a comparison is made between the two CFD model results and the semi-analytical equations for buoyancydriven flow. V=0.2 m/s Fe r i - m e ce- f te e Figure 30: CFD results for combined model in the center of the rooms: velocity vectors 51 Indoor Temperature Gradient Through Three Floors 9 26 3 8 3 . 30.6 30.0 30.329.6 28.7 28.7 7 6 2.- 5 8.1 P) 10- 30.0 28. 2. _ N5. 3 25.28. J,- 4 2 28.1 8.1 27.1 0 24 .9 (a) 26 28 30 Indoor Temperature (C) 32 (b) Figure 31: CFD results for combined model in the center of the rooms: (a) temperature contours (oC), (b) plot of temperature vs. height 4.4.3 Results and Discussion The CFD simulations for both models seemed to give reasonable buoyancy-driven flow patterns, with colder air entering the room at the lower opening and warmer air exiting the room at the upper opening, while also exhibiting temperature stratification characteristics. However, the ranges of values for the velocity and temperature fields for the indoor and combined stack models were different from one another. In order to make a suitable comparison between these two models, the airflow rates were calculated and compared with the semi-analytical calculation from Section 2.2.1. As a result of this comparison, these airflow rates were found to vary for each model and for the semi-analytical calculation, as shown in Table 4. The semi-analytical solution with Equation 4 produced an airflow rate of 9.84 air changes per hour (ACH) at a AT of 2.83oC. The CFD simulations produced airflow rates of 5.42 ACH for the indoor stack model and 10.82 ACH for the combined indoor and outdoor stack model. The airflow rate for the combined model was taken at the lowest apartment, since semi-analytical calculations do not take into account the increasing shift in indoor temperature that has occurred in this situation. When compared with the semi-analytical calculation results, a 41% and 10% difference was found in the airflow rates for the indoor and combined models, respectively. The most important source of difference between the two model results was the choice of boundary conditions. These conditions dictated the flow patterns and temperature profiles within the space. It is necessary to take into account the outdoor hydrostatic pressure difference across the openings in order to provide the correct indoor and outdoor airflow. Otherwise, a zero-pressure condition at all openings will not give appropriate airflow results, making the indoor stack model not physically reasonable. The combined model therefore has a more solid physical background than the indoor stack only model. The airflow rate determined by this combined model produced 52 consistent results when compared with the semi-analytical calculation. Note that the calculation used a temperature difference that was obtained by solving both the semi-analytical calculation and an energy balance for the room simultaneously, as discussed in Section 2.2.1. It is important to realize that the semianalytical calculation assumed isothermal conditions within the room. This assumption is not appropriate for single-sided ventilation because thermal buoyancy relies on temperature stratification within the room to create air movement. Table 4: Comparison of air change rate (ACH) results for various models ACH 9.84 5.81 10.82 Method Semi-analytical calculation Indoor stack model Combined indoor and outdoor stack model (lowest apartment) Percent Difference (%) (standard of comparison) -41 +10 A phenomenon was also observed and mentioned for the combined model that could not be predicted in the indoor stack model or the semi-analytical calculations. Although the spaces were physically and thermally isolated from one another, the temperatures in each space increased with height due to the outside thermal plume from the openings underneath, as was shown in Figure 31. Although in reality the plume can be easily destroyed by wind, the indoor stack model and the semi-analytical equation cannot predict the impact of such a plume. Based on the analyses and results above, the combined indoor and outdoor flow model is an appropriate tool for studying and designing single-sided ventilation. Buoyancy-driven flow has proven to produce results in CFD that are consistent with semi-analytical solutions and should therefore be used for further analysis and design. 4.4.4 Trends in Thermal Buoyancy Study Results The results obtained in the previous section were further extended in order to evaluate the overall trends in buoyancy-driven flow for single-sided ventilation. This incorporated flow through both an upper and lower opening geometry, as discussed previously, as well as flow through a single opening. For this extended study, the heat load within the room was varied between 100 W and 1000 W. This is useful in evaluating the resulting airflow rates over the variation in AT produced between typical indoor and outdoor environments. These cases were simulated for both upper/lower and single opening geometries. For the single opening geometry, a 0.65 m W x 1 m H window was modeled, as shown in Figure 32. These dimensions were chosen based on the single opening geometry used in the upcoming wind study, which reproduces a single-opening empirical model. 53 4:: Figure 32: Combined indoor and outdoor stack model for a single opening geometry in CFD The airflow rate results for both cases, under the range of heat loads given, were compared with the semi analytical equations (Equations 4 and 7) of Section 2.2.1. The results for the upper and lower window and for the single window geometries are plotted in Figure 33. Based on this plot, the CFD results are again found to be within 10% of the semi-analytical solution results. These ventilation rate results are therefore consistent with the semi-analytical results over the range of heat loads and for both a single and upper/lower opening geometry. CFD has proven to be a reliable, valuable tool in analyzing buoyancy driven single-sided ventilation over a range of conditions. 54 12 10 - - --- 2 -e 0 0 200 0 800 600 400 1000 Heat Load (W) - -- Semi-Analytical Upper/Lower 0 OFD Upper/Lower Semi-Analytical Single * CFD Single _____ Figure 33: Semi-analytical and computational air change rate (ACH) results over a range of internal heat loads for an upper and lower opening and single opening geometry 4.4.5 Conclusions This thermal buoyancy study used CFD techniques and semi-analytical equations to determine the ventilation rate in a room with single-sided buoyancy-driven ventilation. The CFD modeling was found to be a very useful means of analysis. The most important aspect of modeling was how to correctly set the boundary conditions. The present investigation used two different models to set the boundary conditions: an indoor stack model and a combined indoor and outdoor stack model. The two models produced quite different airflow rates at the ventilation openings, and the flow rate calculated with the combined model was found to agree more closely with semi-analytical equations. The combined model results were within a 10% agreement of the semi-analytical solution. The combined model also allowed for the prediction of conditions along the height of the building that would otherwise be unknown with the indoor stack model or the semi-analytical equations. By then applying the combined indoor and outdoor CFD model to a single window geometry, along with varying the room heat loads for both window geometries, the model was shown to be robust, producing results that were also within a 10% agreement over this range of varying conditions. CFD has therefore proven to be an important and powerful tool in the analysis of natural ventilation design. 4.5 Wind and Stack Study After determining the buoyancy effects on single-sided ventilation flow, the effects of both wind and combined wind and buoyancy were studied using a new CFD model. This model combined indoor and outdoor airflow similarly to the previous model, but defined different domain boundary conditions than before and extended the domain further in each direction to account for wind effects. 55 In order to evaluate the validity of CFD ventilation rates for wind and combined-driven flow, these results were compared with those of the two empirical models discussed in Section 2.3.1: (1) British Standards model, and (2) Phaff and deGids' model. The current student room model was adjusted to fit the parameters of the Phaff and deGids experimental setup. This involved basically changing the window geometry to that of a single opening and the window size to that of the experiment [24]. This was done in order to be consistent with the experimental setup for comparison purposes, with the intent of then using the actual student room model for further parametric studies. The British Standards model did not provide information regarding the experimental setups from which its model was derived. This model is stated in the literature as applicable for the general case of single-sided ventilation through a single opening. 4.5.1 Wind and Stack Model The CFD wind and stack model was set up in three dimensions and was based on the three-story apartment setup from the buoyancy-driven case. These apartments were bounded by blockages on either side and on the back to create an aspect ratio of 3, similar to that of the actual student residence building (Figure 34). Otherwise, the results from the current three-story apartment model would simulate the wind effects of a high-rise building. Due to the limitations of computational power and grid size, the entire 10story student residence building was not modeled. Due to the larger domain required for wind-driven flow and, in turn, larger grid number, there was a need to minimize computing time in this calculation. Modeling the winddriven flow case in two dimensions was initially considered. A guiding rule of thumb that can determine whether or not it i appropriate to model a particular building in 2-D is: if the aspect ratio of the building is less than 10, then a 2-D assumption is not appropriate. The student residence building studied, with an aspect ratio (W/H) of approximately 3, should not be modeled in two dimensions. All three dimensions were required for this airflow model case. Within the three dimensional model, in order to ensure that the outer domain had no effect on the airflow around the building, the wind profile inlet was placed at 5 buiding heights in front of and to either side of the building. The re-circulation zone for airflow around a three-dimensional block is reported to be approximately 5-7 times the height of the block [46]. Therefore, the outlet was safely placed at 10 building heights downwind of the building to ensure no disturbance of the flow. The upper boundary, placed at 4 building heights above the building, was found to have no effect on the airflow. 56 (a) 4H ........ ... (b) Figure 34: CFD domain for wind and stack model: (a) upper/lower opening geometry and (b) single opening geometry After establishing the appropriate domain size for the CFD wind and stack model, various studies were performed in order to determine the effects of both wind and stack on single-sided ventilation. First, in order to validate the various CFD ventilation rate results obtained for wind and combined-driven flow, the CFD model had to fit the parameters of the detailed empirical study of Phaff and deGids discussed in Section 2.3. The most significant adjustment that had to be made was to the window geometry. Since the experiments performed by Phaff and deGids were based on single opening geometries, the single opening model from Figure 32 was used within the wind and stack domain. A comparison of the setup for the single opening CFD model and that of the three experimental cases is shown in Table 5. Since the room volume and floor area for the student residence case and that of the experiment are very similar, these parameters were not changed. The upper and lower opening room model shown in Figure 34a was therefore replaced with the single-opening room model shown in Figure 34b, while all other conditions remained the same. The experimental setup and single opening CFD models are very similar and could therefore be compared. Table 5: Comparison between experimental and CFD setup .e. Experiment CFD Single Dimension (values averaged for three spaces 1241) Opening Model Room volume (m) 38.0 38.2 Floor Area (m') 12.7 13.7 0.65 0.65 2 Window Area (m ) The CFD single opening and upper/lower opening models were simulated for various cases of wind and combined wind and stack. Meteorological wind speed was assumed to be in the range of 1-10 m/s. Since the empirical equations of Phaff and deGids are based on meteorological wind speed (see Equations 14 and 15), and outdoor CFD modeling relies on setting site (local) wind conditions, a correlation had to be made between meteorological wind speed and the urban environment in which the experiments took place. The correlation that exists between meteorological and local environments is discussed briefly in the following paragraph in order to provide a background into studying all types of local environments. 57 Correction factors are necessary when addressing the variables of both wind speed and outdoor temperature. The shape of the vertical profile of the wind speed depends mainly on the degree of roughness of the surface, determined by buildings, trees and any other obstructions that hinder the flow of wind at the surface. Wind speed values must therefore be adjusted according to the type of local environment studied - i.e. city, urban, country, or rural. A representative wind profile has been established for each of these four local environments, accounting for ground obstructions typical of the particular environment. These local wind profiles relative to ntteorological wind speeds are given by Vh KVmetha (18) where Vh is the local wind speed at height, h, V, is the meteorological wind speed (usually taken at lOim), and K and a are coefficients determined by the local environment and defined in Table 6 [10]. Since the experiments performed by Phaff and deGids took place in an urban environment, this appropriate wind profile was chosen from Table 6 and applied to the CFD wind and stack model at the inlet, located upwind. Table 6: Values of coefficients for Vh=KV metha under local environment conditions 1101 Nature of terrain Open flat country Country with scattered wind breaks Urban City K 0.68 0.52 a .17 7.2W 7.3Y 0.2T 7.2Y 33 When analyzing outdoor meteorological temperature data relative to city environments, it is also important to consider the heat island effect of city centers, which increase the average outdoor temperature a degree or two more than the meteorological value. However, this effect has been shown to be not significant for daytime temperatures but more significant for nighttime temperatures [38]. Local wind profiles were taken into account during this study, but temperature corrections accounting for heat island effect were not applied. Since the empirical model was based on the experimental results from the lowest apartments of hree buildings, the following CFD analysis focused on the results from the lowest apartment. The results from this investigation were ultimately used in order to develop trends for single-sided ventilation. In order to use both the Phaff and deGids model and the British Standards model for comparison purposes in the current single-sided ventilation study, the results from the two models need to be evaluated in relation to each other. This evaluation is performed in the following section. 4.5.2 Comparisonof EmpiricalModels The British Standards model and the Phaff and deGids model are two well-developed empirical solutions for predicting ventilation rates of single-sided ventilation through a single opening. The equations and explanations for each of these methods are outlined in Section 2.3.1. In order to evaluate the similarity between the two models, a comparison was performed for the student residence case over a range of meteorological wind speeds, 1 - 10 m/s. The results from this comparison are based on input parameter values from the previous student room CFD models, with an internal heat load of 700 W and an outdoor air temperature of 25.5oC. Note that the indoor temperature calculation here was based on a temperature difference that was obtained by solving both the appropriate empirical ventilation rate equation and an 58 energy balance for the room simultaneously. The results from this comparison are shown inFigure 35 for the combination of wind and stack effect. The results of the two empirical models are very similar, which in turn strengthens the validity of each of the model's cases. Both models will therefore be used as a basis for comparison when performing the following wind and stack model study. 0.40 - ------ - --- - - 12 0.35 -----030 01 0.25 - > 0.20 -'6 0.15 ~_- 0 .10 - -_-_-- - > 0.05 U 4 - - 2 - 0.00 0 0 6 4 2 Meteorological Wind Speed (m/s) 8 10 Phaff& deGids British Standards Figure 35: Comparison of empirical model results from British Standards and Phaff and deGids: combineddriven ventilation rates through a single opening for the student room model 4.5.3 Comparison of CFD and EmpiricalResults for a Single Opening After an appropriate wind and stack CFD model was set up, various simulations were run over a range of wind speeds, 1-10 m/s. The ventilation rate solutions were then compared with those of two empirical models: the British Standards model, and Phaff and deGid's empirical model. This comparison is shown in Figure 36. 59 0.40 - 0.35 12 - 10 0.30 01 ~J0.25 - 8 -- 8 0.15 > 0.25 ----- 0.10 > 2 0.05 0.00 0 0 2 4 6 Meteorological Wind Speed (m/s) __ x 8 10 Phaff&deGids British Standards CFD Figure 36: Comparison of CFD results with empirical model results: combined-driven ventilation rates through a single opening for the student room model CFD predictions have shown to underpredict the ventilation rates for a space by approximately 25% for velocities between 1 and 10 m/s. This may be due to the fact that RANS modeling in CFD solves for average airflow parameters rather than instantaneous airflow, which is believed to be a major component of the driving force for single-sided ventilation. This is supported by the fact that the LES tool, which solves for instantaneous flow parameters, has been found to correctly predict experimental ventilation rates in the literature [32, 33] Therefore, it may be the case that RANS modeling underpredicts wind or combined-driven ventilation rates by approximately 25%. Other computational studies that were found in the literature have also found this approximate percent difference in results [47]. 4.5.4 CFD and Curve-FitEmpiricalResults for an Upper andLower Opening The empirical models of the British Standards and Phaff and deGids were based on a single opening geometry. In order to evaluate wind and buoyancy-driven ventilation rates for the actual student room models, with the upper and lower openings, a new model needed to be developed since no experimental work has been performed in this area. Modifications had to be made to the empirical models for both wind and stack effect. The approach taken for these unknown quantities was to derive the modified empirical models from CFD results for the upper and lower opening case, assuming that an underprediction of 25% is similarly present. The CFD results for combined wind and stack effect on single-sided ventilation through an upper and lower opening were therefore determined over a range of meteorological wind speeds of 1-10 m/s. These results are shown in Figure 37. The ventilation rates produced by combined-driven flow for this window layout have greatly increased over those of a single opening, which is expected given the favorable conditions of the upper and lower opening layout over the single opening layout on indoor airflow for single-sided ventilation. This opening layout has shown to be advantageous for both wind and stack effects within the CFD results. From these results, a curve fit was performed for the British Standards model and the Phaff and deGids model to produce a reasonable prediction of combined-driven ventilation rates through upper and lower openings. 60 First, the single-opening empirical model developed by Phaff and deGids was modified to account for the different opening geometry. The buoyancy-driven airflow rate for an upper and lower opening is stronger than that of a single opening - approximately three times stronger according to the simplified theoretical equations discussed previously in Section 2.2.1. To account for this difference in buoyancy-driven flow between the experimental single opening setup and the computational upper and lower opening setup, the C2 term from Equation (5) was adjusted accordingly. The turbulence term remained the same as the original empirical model since this is a constant value independent of varying conditions. However, the possibility of a difference in wind effect between the opening geometries was seen in the remaining difference between airflow values - this difference was incorporated into the C1 term of the wind term. The C1 values were determined to increase from 0.001 to 0.004, increasing the ventilation due to wind by approximately two times. The resulting calculation below is therefore a combination of the simplified theoretical solution for an upper and lower opening, the empirical model acquired from the detailed experiments of Phaff and deGids, and CFD modeling. - Veff A = 0total .004 Vmet2+0.0105 -hAT +0.01 (19) If the local wind speeds at a site are used instead of meteorological wind speeds, Equation 19 takes a more general form, Vtotal _ V0.01iVoca2 vf A +0.0105-hAT+0.01 (20) A similar curve fitting process was performed for the British Standards model for a single opening. The buoyancy-driven ventilation rate was simply modified from the semi-analytical solution for a single opening to that of an upper and lower opening geometry, discussed in Section 2.2.1. This buoyancydriven ventilation rate for upper/lower opening geometries is actually part of the British Standards model. However, a corresponding wind-driven ventilation rate for this opening geometry was not established within this method. Therefore, the wind-driven ventilation rate was modified from its original singleopening form, in Equation 10, by increasing the coefficient from 0.025 to 0.1, which effectively increases the ventilation due to wind by approximately two times. AT -tack Vwind Vtotal dAgh At (21, 22, 23) =0. 1AVocal (1V(stack )2 + (-wnd2 The graphical representation of these modified empirical models developed for single-sided ventilation through an upper and lower opening due to both wind and temperature is shown in Figure 37 for the student residence case, along with the CFD model results, upon which they were based. 61 0.7 ' -25 0.6 20 0.5 X1 -~0.4 0.3 - 0.2 X - _10 X 5 - 0.1 0.0 0 0 2 4 6 Meteorological Wind Speed (m/s) Phaff&deGds X 8 10 British Standards CFD Figure 37: Modified empirical models and CFD results for combined wind and bouyancy-driven ventilation rates through an upper and lower opening (in order to predict single-sided ventilation rates through an upper and lower opening geometry, modified empirical models were derived from CFD results, assuming a 25% difference) 4.6 Wind Direction Study Although the British Standards method and the empirical model derived by Phaff and deGids provide simple relationships for deriving single-sided ventilation rates, these equations only consider buildings with an opening in the windward wall and with wind directed perpendicular to the window. Other factors, such as the effect of wind direction, are not considered. To study the effect of wind direction on singlesided ventilation, more detailed and concrete methods are therefore needed. In this next part of the study, a series of CFD simulations were performed on a full range of wind directions, 0, to determine what types of trends were found in single-sided ventilation rates at various angles. For the purposes of this study, o refers to the angle between the directed wind and the normal to the building facade plane being studied. A sample velocity vector plan view foro = -45o is shown in Figure 38. 62 77/7/777/' MlMM77//7777777 Figure 38: Wind direction CFD study: 7 7 overall plan view of CFD domain for 0 -45* The overall findings from this CFD study are shown in Figure 39, which plots the relationship between wind direction and a dimensionless ventilation rate (based on a maximum ventilation rate at 0=0'). However, for the guideline tools developed in this study, wind-driven ventilation will only be considered on the windward side of the building, i.e., from -90' (wind flowing parallel to the facade in one direction) to 90' (wind flowing parallel to the facade in the opposite direction). This was done for two reasons: (1) there are no concrete experimental studies that have been performed which determine the effect of wind direction on single-sided ventilation rates, and (2) CFD RANS modeling has proven to be weak in the area of modeling airflow on the leeward side of a building, as clearly shown in Chapter 3. Although CFD cannot be validated for these varying wind directions, it is believed that CFD has provided a strong case through validation for modeling airflow on the windward side of a building, and the results from-90' to 90 can therefore be trusted. 63 04 00 G.2 -180 -135 -90 -45 0 45 90 135 180 Wind Direction, 0 (degrees) CFD overall trend ------- curve fit for windward angles =cos 0 x Figure 39: CFD overall findings for the impact of wind direction on single-sided ventilation rates and a simple curve fit relationship for angles along the windward building facade ((=angle between directed wind and plane normal to building facade) In order to modify ventilation rate equations found and developed so far in this study, which are based on perpendicular wind speeds, the wind-driven ventilation term in the empirical models was multiplied by a (cos o) term according to the best fit curve in the range of-90 to 90 from Figure 39. This cos term is a simplification based on the CFD curve found in this figure. Modifications to the British Standards winddriven ventilation rate therefore produce Vwind(sin (24) gle) = 0.025AVocal cos 0 Vind (upper / lower) = 0. 1AVocal cos 0 Similarly, the wind-driven ventilation term determined by Phaff and deGids is modified to account for wind direction, vwind (sin gle) = A -. 00l(Ve cos 2 Vwind (upper / lower) = A A 2 0)2 = 2 .0026(Viocal cos 0)2 (25) .004(Vmet cos ) 2 = A .0 (Vioca, cos 0)2 These terms are then incorporated into the total ventilation rate due to both wind and stack, which is summarized in its final form for both empirical models in Table 7. This table summarizes all the results from the buoyancy, wind, and combined-flow parts of this study. 64 Table 7: Summary of Ventilation Rate Terms for Empirical and Modified Models 123, 241 British Standards Model Term Single Opening C A 3 Phaff and deGids Model Upper/Lower Opening AT CdA gh g hstack Tou AT Tut wind Single Opening Upper/Lower Opening A 0.0035-hAT 2 A10.0105 - hAT** 2.001(Vmet COS 0.025AVial cos0* Y AV.004(Vmet COS) (for urban environment only) (for urban environment only) or or 0.lAVocai COS ** .0026(V 0 oc 1 cos 0)2 A turbulence A .01(Vicai cos 0)2 4 * **- A00 - 2 - (Vstack )2 + (-wind total )2 (stack )2 + ( ,0.00l -(V. cos0) 2 + 0.0035 -hA T + 0.01 (for urban environment only) 22ind A jo.004 -(Vm, cos06) 2 + 0.0105 - hAT + 0.01 ** (for urban environment only) sr or A 0.0026-(V cos0)2+ 0.0035 -hAT + 0.01* A O.0I- (V cos0)2+0.0105.hAT+0.01** *Note: Ventilation rates were not completely determined within referenced empirical study. Simple adjustment for wind direction (cos 0) was made. **Note: Ventilation rates were not completely determined within referenced empirical study. CFD results were used to modify these terms. Although the (cos o) term is a simplification based on CFD trends, shown in Figure 39, it is believed to be valid for determining approximate ventilation rates at various angles on the windward side of a building. Based on geometric principles alone, it is intuitive that the windward ventilation rate would vary as coso by simply calculating the component of the wind speed perpendicular to the opening. It must however be realized that validation of this part of the study was not possible due to the lack of research performed on the impact of varying wind directions on single-sided ventilation rates. 4.7 Counteracting Wind and Stack Study Although experiments have found, for a particular tested room, that wind and stack flow reinforce each other according to the relationships in Equation 13 and 14, there is also evidence that, on a case by case basis, wind and stack forces do not always reinforce each other, but in fact oppose each other. This ambiguity is illustrated in Figure 40a. An example of the counteracting wind and stack effect during an increasing progression of wind speeds is also shown in Figure 40b. Tout TM wind wind stack U stack (a) I E STACK 4 m/s 3 m/s 2 m/s m/s WIND>STACK STACK>WIND I WIND>>STACK (b) Figure 40: The uncertain effects of combined wind and stack forces: (a) reinforcing vs. counteracting effect (b) depiction of counteracting wind and stack effect over a progression of wind speeds Although the study has concentrated so far on the airflow through the lowest apartment (for comparison with the empirical models), it was noted during this study that a counteracting wind and stack flow did in fact take place in the middle apartment of the CFD wind and stack model for both window geometry types. The physical phenomenon was found to be very similar to that demonstrated inFigure 40. In order to illustrate these findings, the CFD wind and stack model for an upper and lower opening was evaluated and shown at a center section of the middle apartment. Velocity vectors were taken at a plane through the center of the middle apartment for meteorological wind speeds varying from 2-8 m/s. Initially, at a low 2 m/s wind speed, buoyancy effects were dominant and consequently drove air in through the lower opening and out through the upper opening. At a wind speed of 4 m/s, this buoyancy effect diminished as the wind-driven force through the upper opening increased. The buoyancy and wind forces were approximately equal at this wind speed, resulting in the minimum ventilation rate over the range of wind 66 speeds given. As the wind speed increased to 6 m/s, the wind-driven force became dominant, thereby forcing a counterclockwise flow into the apartment, in through the upper opening and out through the lower opening. At 8 m/s, this wind force simply became stronger, with buoyancy effects becoming nearly negligible. A" AA ~ t ~t - Vmet 2 rn/s Vmet - I Vmet 6 0.4 4 m/s mIs m/s ->e=04ms Vmet =8 m/s Figure 41: Counteracting wind and stack effect in middle level apartment of CFD wind and stack model over a progression of wind speeds, for upper/lower window geometry Although there are unfortunately no guiding rules to help in determining where the counteracting wind and stack effect occurs will occur along a building's facade, designers should be made aware of this physical phenomenon to better understand the characteristics of natural ventilation. In order to develop a set of rules for predicting this phenomenon, various different building sizes and shapes would need to be studied and modeled. One observation that was made, after setting up a CFD model of several stories, was that along the center-height apartments, where the wind splits direction downward and upward along the building face, the apartments along the downward wind direction experienced a reinforcing wind and stack flow, while those along the upward wind direction experienced a counteracting wind and stack flow. However, this phenomenon was only observed along the center grouping of apartments. One area of future research that may be necessary is to determine some types of general rules for evaluating where this type of phenomenon is most likely to occur along a building. 4.8 Mixed Mode Ventilation Study After a detailed analysis of the performance of the single student rooms for Boston weather conditions, it becomes clear that natural ventilation is not feasible at all times in particular climates. This situation is 67 very typical of many US climates, which may have seasons of particularly extreme weather, unsuitable for natural ventilation. Rather than recommend mechanical ventilation or air conditioning for buildings in these climates, other more energy efficient possibilities need to first be explored. Conditions in which natural ventilation is not possible may not require reverting to complete mechanical ventilation- this is not the only alternative. A compromise of strategies is another alternative that must be investigated, i.e. mixed-mode ventilation. Within the single student rooms, designers on the project have considered a few options over the course of the design. These options have been analyzed within this section to discover the potential opportunities and downfalls that present themselves within mixedmnode ventilation strategies. CFD has been used as the primary tool in this investigation. 4.8.1 ConcurrentMixed Mode Ventilation - Low Cooling A major component of the student residence building designed by Steven Holl Architects, on the campus of the Massachusetts Institute of Technology (MIT), was to make the single room units for the student residents allow for natural ventilation. However, due to Boston summer weather conditions, itis believed that mechanical cooling must be provided to allow for adequate thermal comfort of the occupants. Therefore, it was proposed during the design process to implement a low-cooling (i.e., low volume flow rate) displacement ventilation system within each room, with an inlet at a low flow rate of 50 CFM (0.0236 m3/s) and air temperature of 13oC along the back wall at floor level and the outlets provided by the upper window. This room was designed with a low-cooling system, with the intent of utilizing both mechanical and naturally ventilated air in the space. Otherwise, a 50 CFM mechanical system can only remove a small percentage of the 700 W heat load within this room, which can be readily assumed. Initially, the lower window was closed because air from the diffuser might be short-circuited to the outside air, wasting input energy to the apartments. In order to evaluate the feasibility of this design, a CFD study was conducted for this setup, as shown in Figure 42 (with the lower window in this model closed). In addition, a CFD study was then performed on the same setup with the lower window open to determine the impact of this displacement ventilation system on the indoor airflow and temperature fields for these two operational setups. Figure 42: Low-cooling displacement ventilation system proposed for student rooms 68 The CFD study, continued from the previous studies done on the available natural ventilation through this room, was modified to include an inlet located below the bed. The assumed heat sources within the space consisted of a computer (300 W), television (300 W), and the occupant (100 W). The two design simulations were performed for a worst-case situation - i.e., no wind was present. The room setup shown in Figure 42 was therefore placed within the stack model domain of Figure 29. This was necessary as a result of the conclusions drawn from the thermal buoyancy study on modeling combined indoor and outdoor airflow. After the CFD model was set up, simulations were run for the 700 W case. The airflow pattern that occurred as a result of this setup was that the upper opening acted like a single opening for buoyancydriven flow (i.e., air entered through the lower half of the opening and exited through the upper half of the opening), while the displacement ventilation system provided an upward airflow pattern into the room, shown in Figure 43. Since the window opening was at the upper part of the room, the natural outdoor ventilation "system" behaved more like that of mixing ventilation than of displacement ventilation. Since there were two forms of counteracting ventilation strategies therefore present, the airflow converged in the middle part of the room, where the cold upward stream from the mechanical displacement ventilation system met the downward flow of the natural mixing ventilation. The air from both streams then exited the room through the upper half of the window. The ventilation rate for the entire room was calculated to be 4.11 ACH, much lower than the buoyancy-driven natural ventilation rate of 10.82 ACH determined in Section 4.4.3. This may be due to the fact that the strong indoor air mixing created by the upper opening, by counteracting the upward buoyancy effect, results in a lower air change rate. A diagrammatic and computational representation of the observed flow is shown in Figure 43a and b, respectively. 69 mechanical +natural mechanical WPW-q .- . -- - - - -- - - - -- --- M MP@qNW4MdM4PNW" I. I [ naturali -4k, Nfl a .. inin (a) V=0.2 m/s o f Figure 43: Low cooling displacement ventilation system with only upper windows open: (a) diagrammatic airflow pattern, (b) velocity vector field 70 The temperature profile was then examined to determine the level of comfort provided by this system, shown in Figure 45a. The temperature directly above the occupant in the lowest apartment was found to be 28.7'C. This is about the same as the indoor conditions provided by natural ventilation through an upper and lower opening, determined from the stack CFD model in Section 4.4.2 to also be about 28.7'C for an outdoor temperature of 25.5 C. It was also necessary to validate whether opening the lower window would have a negative or positive effect on the indoor airflow and temperature distribution. The combined indoor and outdoor stack model of Figure 29 was again used with the room setup of Figure 42 in order to evaluate this issue. Outdoor temperature was set at 25.5 'C, similar to previous studies, while the indoor heat load remained at 700W. The resulting airflow pattern was that of typical buoyancy-driven flow into the lower opening and out of the upper opening, with an additional flow of mechanically ventilated air out through the bottom part of the lower opening, shown in Figure 44. This did in fact prove that part of the displacement system air would be short-circuited to the outdoor environment. However, the majority of this mechanically treated air did combine with the incoming outdoor air to cool the conditions within the room. The ventilation rate for the entire room was calculated to be 6.94 ACH, lower than the buoyancy-driven natural ventilation rate of 10.82 ACH from Section 4.4.3, but higher than the ventilation rate of 4.11 ACH from closing the lower window in this mixed-mode system. A diagrammatic and computational representation of the observed flow is shown in Figure 44a and b, respectively. 71 mechanical +natural mechanical Snatural bhj.'- :1 - -77 CI .I1.1, 1, (a) -- V=0. 2 m/s I*.i Figure 44: Low cooling displacement ventilation system with upper and lower windows open: (a) diagrammatic airflow pattern, (b) velocity vector field Despite the short-circuiting of some of the mechanically ventilated air, the temperature distribution proved to be favorable for this setup, with an air temperature of 26.7oC directly above the occupant in the 72 lowest apartment (2'C cooler than both the natural ventilation stack case results of Section 4.4.2 and the previous mixed mode case), shown in Figure 45b. 2627 25.9 CNJ 29.625.3. 30. 30 30.1 07 22.4 21.8 21.8 4 2 '8.7 29.9 3 . 0.1 28.9 27.82. 28.7- 25.6 27.3 21.8 19. 2 24.4 -21.8 20.4:, 22.2 22.2 20.0 2 27.8 -- __25.5 20.4 __-24. (a) 26.7 25.5 233 24.4- 21.1 - _22 .(b) Figure 45: Low cooling displacement ventilation systems: temperature contour fields for (a) only upper window open, (b) upper and lower windows open (*C) Table 8 shows the results from these two mixed-mode cases, as well as from the buoyancy-driven natural ventilation case of Section 4.4. Providing natural ventilation through both the upper and lower openings was found to produce more thermally comfortable results (lower temperatures and higher ventilation rates) for this low cooling system and is therefore the preferred operating mode to achieve the most effective mixed mode ventilation system for this specific situation. This may be due to the fact that the mechanical ventilation system was a very low cooling system, and therefore, by providing cool air at a very low ventilation rate, the outside air was allowed to penetrate the space and mix with this "slowmoving" treated air, creating an upward airflow at a temperature between the outside and mechanical air temperature. On the other hand, if a higher mechanical ventilation rate was introduced to the space, this system may operate more favorably with the lower window closed, encouraging a strong upward displacement force through the room, while discouraging this higher velocity airflow from easily shortcircuiting out through a lower opening. The effect of an open lower window is therefore thought to be more detrimental at higher mechanical ventilation rates. However, for the current system, the mechanical ventilation rate is too low to have a negative effect, and therefore creates better indoor conditions by allowing the lower window to be open and introducing outside air into the space. In addition, a low cooling mechanical ventilation system requires less energy than a typical system that is required to meet the full heat load requirements of a particular space. 73 Table 8: Mixed-mode ventilation results compared with natural ventilation Parameter Air Temperature (oC) Ventilation Rate (ACH) Mixed-mode Ventilation: Upper Window Open 28.7 4.11 Mixed-mode Ventilation: Upper and Lower Window Open 26.7 6.94 Natural Ventilation 28.7 10.82 The current proposed mixed mode system, assuming the upper and lower windows are open (optimum operational mode), presents favorable conditions within the student room. While the ventilation rate of this system is lower than that of natural ventilation (6.94 ACH versus 10.82 ACH), the system compensates for this lower airflow with a 2oC decrease in indoor temperature conditions. The potential for such a decrease in air temperature can have a large impact on the extreme summer conditions within certain climates. This can be readily seen in the following section when analyzing indoor conditions over the entire month of July within Boston, MA. A 2oC decrease in indoor temperature conditions will have a great impact on thermal comfort, by helping to shift the indoor temperature distribution range, seen in Figure 53, to be more within the thermal comfort zone. Another advantage to having this mixed-mode system, in which a percentage of the air entering the room is mechanically treated, is that relative humidity levels canpotentially be lowered, due to the reduction in volume flow of humid, outdoor air that is partly replaced by mechanically cooled air into the space. 4.8.2 Cross Ventilation Duct System For single-sided natural ventilation design of the student residence building on the MIT campus, the designers realized the need for more optimal ventilation rates. Single-sided ventilation design cannot always provide a high enough ventilation rate to a space, due to the limits that having an inlet and outlet on the same facade place on the system. Cross ventilation, on the other hand, generally provides higher ventilation rates because this strategy can take advantage of the positive pressures on the windward side and negative pressures on the leeward side of a building to force high velocity air through the space(s). For this reason, designers sometimes consider modifying single-sided spaces in such a way to take advantage of these large pressure differences across the building facade. One design option that was suggested for the single student rooms was the use of a duct system to provide a type of cross ventilation across an entire floor of the residence building. An appropriate duct system was analyzed and sized for this application [48], based on an average meteorological wind speed of about 6 m/s for Boston, MA. This duct size was determined to be 10 in. x 24 in. (0.254 m x 0.61 m). This duct system was then evaluated in the current section using the CFD wind and stack model, with modifications made. A section view of the building setup is shown in Figure 46. In this figure, the duct system is applied to the lowest floor only, in order to save on computing time. The duct entered both the windward and leeward spaces through the ceiling at the center section of the room. 74 Figure 46: Section view of duct CFD model on lowest floor apartments; this case is a modification of the building within the existing CFD wind and stack model From this CFD study, ventilation rates and indoor air temperatures were evaluated for this natural ventilation strategy. The purpose of this design would primarily be to improve ventilation rates through the rooms, by providing a form of cross ventilation. An overall airflow diagram and a velocity vector field for this duct design is shown in Figure 47. The improvement in ventilation rate over that of natural single-sided ventilation is evident from the magnitudes of the velocity field. Upon calculating the ventilation rate, an ACH of 28 was determined. For this same setup in the earlier single-sided ventilation study on wind and stack, for a 6 m/s wind and an upper/lower window geometry, an ACH of 12 was found. Therefore, this modified design case provided a ventilation rate that is at least 2 times higher than that of single-sided natural ventilation in the windward room, under the same outdoor conditions. These results are very promising for the use of this duct system in spaces where single-sided ventilation rates are not sufficient. 75 (a) V= (1 4- ~~~~III'---*~~ mI/ I' 4(1" V/114 * 4, 1I *0 0 I (b) * 4 I Figure 47: Cross ventilation duct system: (a) diagrammatic airflow pattern, (b) velocity vector field The temperature contour diagram for the cross ventilation duct system is shown in Figure 48. For this same setup and conditions in the earlier single-sided ventilation study on wind and stack, an average room temperature of 27.2oC was found. Comparatively, the overall temperature distribution in this cross ventilation case is optimum in the windward room with an average temperature of approximately 27.1 oC, but has slightly worse conditions in the leeward room, with a corresponding value of about 28.5oC. However, this design is still believed to produce indoor conditions that are satisfactory, especially given the fact that the duct cross ventilation design's goal is to maximize ventilation rates through the rooms. This design is especially promising for the leeward apartments, where the potential ventilation rates are presently unknown due to a lack of concrete information regarding this location. The potential ventilation rates obtained in the leeward apartments as a result of this cross ventilation will most likely be a good deal higher than that of single-sided ventilation, since it is probably safe to assume that the perpendicular windward ventilation rates (0=0) are the highest possible single-sided ventilation rates that can be obtained for a given situation, which was given to be ACH=12 in this case. Ii\ 28.5 C .& 27.5 Figure 48: Duct natural ventilation system: temperature contour field (oC) 76 4.8.3 Conclusions There is a great potential in the area of mixed-mode ventilation, although more research in this area needs to be performed in the future, especially through experiments and new design concepts. However, this brief overview has attempted to introduce two potential mixed-mode ventilation strategies that are being considered for a real building application. The first is a form of mixed mode ventilation called concurrent mixed-mode ventilation (see Section 2.6), where the system provides mechanical and natural ventilation simultaneously. This type of system is very complicated to design, since special attention should be paid to the very likely occurrence of energy being wasted during the process. This was found to occur within the current design when both the upper and lower windows were open. However, at the same time, this operational mode also led to more comfortable indoor temperature conditions over that of the same system with a closed lower window and over that of natural ventilation. Natural ventilation was found to provide better (higher) ventilation rates than those of both mixed mode systems. The mixed mode system in this study has a large potential for those environments with high outdoor temperatures that require more thermally comfortable indoor conditions. Further analysis will be necessary to determine which system is preferable in terms of indoor comfort conditions and energy efficient design. The second mixed-mode system design introduced is a cross ventilation duct system, where the singlesided ventilation spaces along the windward and leeward facades of a building are modified to create a form of cross ventilation through ceiling ducts. This system was found to produce ventilation rates that were at least 2 times higher than that of single-sided ventilation in the windward room. These results show a definite design potential for situations that require higher ventilation rates through the spaces. Mixed-mode ventilation is a potential way in which to satisfy those situations where natural ventilation is not adequate. It is a valuable alternative to air-conditioning, and can provide a great contribution, with the help of further research, to the future design of energy efficient buildings. 4.9 Conclusions The current single-sided ventilation study has been discussed in detail within this chapter. The various design features of this natural ventilation strategy have been explored and analyzed in order to gain a better understanding of the complexities and characteristics of single-sided ventilation. Based on results from analytical, empirical, and CFD models, trends were revealed and validated. Upon validation with analytical and empirical results, CFD models were then applied further to develop results for single-sided ventilation in areas that are currently lacking in research. Some such areas include wind-driven ventilation through an upper and lower opening, the effects of wind direction on single-sided ventilation, the counteracting effects of wind and buoyancy, and mixed-mode ventilation. Although these areas could not be validated, they are strongly supported based on previous studies and provide an overall background study into areas of natural ventilation that have a huge potential for future studies. The first part of the study focused on the buoyancy and wind-driven effects of single-sided ventilation. For buoyancy-driven ventilation, CFD models were established in order to determine the appropriate modeling setup for this highly sensitive temperature-driven flow. Upon detailed analysis, it was found that modeling both the outdoor and indoor environment is necessary for correct airflow and temperature results within CFD. For this combined stack model, ventilation rate results were found to agree with semi-analytical solutions for buoyancy-driven flow, within 10%. This agreement was found to exist over 77 a range of indoor temperature conditions and for different window configurations. The modeling of the outdoor environment produced consistent results with analytical solutions, as well as providing information on the interaction between the indoor and outdoor environment, valuable information that cannot be obtained from a theoretical equation or from setting the computational domain to only include the indoor environment. The wind and buoyancy-driven effects of single-sided ventilation were then investigated with an appropriate CFD model, which calculated ventilation rates over a range of wind speeds. These results were compared with two empirical models from the literature, which were both based on a single opening setup for single-sided ventilation. The two models were very similar, and upon comparing these models with CFD results, the CFD model was found to follow the same trends, but consistently underestimate the ventilation rates by 25%. This source of difference between the CFD and empirical models is believed to be due to the fact that the RANS modeling technique within CFD solves for averaged flow parameters, whereas the ventilation rate for single-sided ventilation is largely dependent on time-varying air fluctuations at the interface of the opening, which create turbulence, a major driving force in single-sided ventilation. Based on this consistent underprediction in combined wind and buoyancy-driven ventilation rates, a CFD model was assumed to follow this behavior and was used to establish curve-fit equations for flow through an upper and lower window opening. Although semi-analytical buoyancy equations have been developed for this geometry, wind-driven and combined-driven empirical models have not been. CFD was used as the tool for this further development, and the results were assumed to underpredict those of the experiment by 25% and were then curve fit to empirical models similar to those set up for a single opening. After establishing and verifying results for the effects of buoyancy, wind, and combined forces on singlesided ventilation, further studies were performed on the effects of wind direction, counteracting effects of wind and buoyancy, and options for mixed-mode ventilation. Although these results could not be validated, the confidence built into CFD modeling of single-sided ventilation over the course of this study has warranted further analysis of this natural ventilation strategy. From these additional research areas, several conclusions were made. For wind direction studies, a curve for ventilation rates versus wind direction was determined. However, since the use of outdoor CFD modeling has found problems in modeling the leeward region of a building, there was a lack of confidence in the results obtained on this part of the building. Therefore, only the results found along the windward side were used for further analysis. This ventilation rate curve followed an approximate path of cos 0. In another brief study, attention was drawn to the counteracting wind and stack effect that was occurring in the middlelevel room of the wind and stack CFD model, where wind was entering through the upper part of the space and exiting through the lower part. This was verified by tracking the velocity patterns through the room at a range of wind speeds. A wind speed existed along the middle of this range that produced a minimum ventilation rate. This occurrence designates the point at which the wind and buoyancy forces are equal. No guiding rules could be established for predicting the occurrence of counteracting wind and stack effect, since no consistent trends were observed, but further research is recommended. Mixed-mode ventilation options were also looked into as possible alternatives to single-sided ventilation designs that do not provide sufficiently optimal indoor conditions. The two types of mixed mode systems analyzed were a low cooling displacement ventilation (combined with natural ventilation) system, and a cross ventilation duct system. Both systems improved conditions within the space slightly, but also created additional issues in the process that needed addressing. This is a very valuable field of natural ventilation that needs a great deal of further research in the future to have a large impact in the field of energy efficient building design. If the possibility to compromise with mixedmode systems is developed and advanced further, applying these systems will be valuable in reducing the high-energy consumption costs that exist in the building sectors today and in creating a better, healthier, more sustainable indoor living environment. 78 CHAPTER 5: DESIGN TOOL AND GENERAL GUIDELINES 5.1 Introduction The single-sided ventilation investigation presented in the previous chapter was performed in order to understand and develop trends in the results to ultimately develop both a simple design tool and general guidelines for this natural ventilation strategy. This chapter compiles the results of the current singlesided ventilation study, detailed in Chapter 4, into two parts: (1) a computer design tool and (2) a simple set of design guidelines. The first part was developed to obtain distributions of indoor conditions over the time span of a month or a year, based on a particular single-sided ventilation design. This tool allowed for a more detailed calculation of conditions, whereas the second part of this chapter, the general design guidelines, only gives ventilation rate results for one given set of inputs. However, this is a good way for designers to obtain an estimate of possible ventilation rates for their design, and modify their design based on these results. These general guidelines enable designers to easily assess their designs for single-sided natural ventilation. The design tool discussed in Section 5.2 is a computer program that was developed, which requires a series of design inputs and then analyzes this design for a given location to determine various indoor conditions, based on the results of the study in Chapter 4. This tool is presently set to analyze designs for any single-sided ventilation space within the climate of Boston, MA. The tool is only designed for natural ventilation in single-sided rooms, since it is based on the current study, but the climate can be varied by replacing the TMY data for Boston with that of another location. The set of design guidelines laid out in Section 5.3 are also based on the analytical, empirical, and numerical results of Chapter 4. When referring to empirical equations, the British Standards model was used for purpose of the guidelines due to it's simple, explicit treatment of buoyancy-driven, wind-driven, and combined driven flow rates. The material within this section may be redundant with past discussions, but is collected together into one cohesive final form to provide a set of simple guidelines for designers to design by. 5.2 Single-sided Ventilation Design Tool Based on all the results found and methods established within the current study discussed in Chapter 4 from semi-analytical, empirical, and CFD results, an overall final task was to produce a single-sided ventilation computer tool compiling all the results and findings from this study. This tool calculates the indoor distribution of parameters (e.g., air temperature, relative humidity, ventilation rate, and thermal comfort) over time based on hourly weather data for a year in order to determine if natural ventilation is in fact feasible for a particular single-sided ventilated design. The computer tool that has been developed can be applied to any single-sided ventilation design and only requires a few simple design inputs in order to perform the analysis. This tool is based on Boston TMY data [44], but can easily be altered to solve for the weather conditions of any city, by replacing the TMY data within the computer tool with that of the desired location. In the following sections, this tool is described by stepping through the process from input design to output conditions to recommendations. To provide a familiar design for demonstrating the tool, the student room case used in the current study, in Cambridge, MA, was used. Both window geometries analyzed and discussed, i.e., single and upper/lower openings, were used as input to this tool, 79 to provide a detailed comparison of performance. This process will help to determine if natural ventilation is in fact feasible for this single-sided ventilation design. 5.2.1 Design Input - Student Room Case The first step that was established in analyzing a particular design for single-sided ventilation was to set up a simple form to input design parameters for a particular building and room, shown in Table 9. This would be representative of the type of form designers would need to complete regarding their design. The input values in Table 9 are those of the student residence building and single room with an upper/lower window in Cambridge, MA (the analysis of which is based on nearby Boston weather data) . The types of inputs required include room dimensions, local environment type, window dimensions and geometry, building orientation and building size. Table 9: Design form for single-sided ventilation design inputs SINGLE-SIDED VENTILATION DESIGN INPUT FORM BUILDING INFORMATION Building Type: Student Dormitory Location (City, State): Cambridge, MA TYPICAL ROOM LAYOUT Room Volume (m2): Floor Area 38.2 2 13.7 (M ): Room Depth (m): 4.7 Ceiling Height (m): 2.8 OUTDOOR CONDITIONS Select City/Urban/Country/Rural*: CITY INDOOR CONDITIONS Indoor Heat Load (W): 700 Number of Occupants: WINDOW LAYOUT Upper/Lower Windows? Yes 2 Upper Window Area (M ): Lower Window Area (M ): 0.4 2 0.4 Height between Windows (m): 2.03 Single Window? Window Area (M 2 ): BUILDING LAYOUT Building Orientation from Predominant Wind Direction 30 (0): Number of Stories: 10 Building Height (m) 30 *City=metropolis Urban=suburbs Country=rural w/trees Rural=flat land 80 5.2.2 Outdoor Conditions- Boston TMY Data Since the sample design was based on a student residence building located on the campus of MIT, weather data were extracted from TMY data [44] for the city of Boston, Massachusetts. For purposes of the sample problem, the analysis was performed over a July month in Boston, MA. Analyzing the design case for July, generally the warmest month of the year, would help to provide a worst case situation for the student room to determine if natural ventilation is in fact feasible for this single-sided ventilated design. Before analyzing the indoor environment parameters, the distribution of outdoor conditions should be first known, based on the weather data provided. Therefore, the distributions of outdoor temperature, relative humidity, meteorological wind speed, and wind direction over the month of July in Boston, MA are shown in Figure 49, Figure 50, Figure 51, and Figure 52, respectively. It is clear from these distributions that designing for natural ventilation in such an environment will be a challenge, especially with regard to relative humidity levels and occasional outdoor temperature levels. ----- 25 - - - I o 20 15 10 5 n-f u 14-16 16-18 18-20 20-22 22-24 24-26 26-28 28-30 30-32 Outdoor Air Temperature (C) Figure 49: Distribution of outdoor temperature for July in Boston 81 32-34 20 .. ~. ~ **..~*...... . . .. . .. ........................ ... .I--.- 15 10 5- 20 -30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 Relative Humidity ( % ) Figure 50: Distribution of relative humidity for July in Boston 25 ........... ... ........ ................ ....................... .... .......... 20 15 U -........ Cj 10 I 5 0 0-1 1-2 2-3 3-4 4-5 5-6 6-7 7-8 Meteorological Wind Spe ed ( m/s ) 8-9 Figure 51: Distribution of meteorological wind speed for July in Boston 82 9-10 20 15 15 10 5 0 0-45 45-90 90-135 135-180 180-225 225-270 270-315 315-360 Wind Direction, 180=directed from south ( m/s) Figure 52: Distribution of wind direction for July in Boston After performing this simple analysis on the outdoor conditions, the student room design was analyzed based on these conditions to determine the potential for natural ventilation. 5.2.3 Design Output - Student Room Case To best determine the feasibility of a particular single-sided ventilation design for natural ventilation, the following parameters were calculated within this new computer tool (the source of the calculation method used to determine these parameters is shown in parentheses): * * * * Indoor temperature Indoor Relative Humidity Air change rate Percentage of Persons Dissatisfied (same as that of air change rate - solved simultaneously) (Appendix A.2) (Table 6, Table 7, and Equation 10) (Appendix A.3) It is believed that these parameters will help in determining the performance of a particular design within this tool. Based on both the inputs shown in Table 9 for the student room and the hour-by-hour TMY weather data inputs for Boston, illustrated in Figure 49, Figure 50, Figure 51, and Figure 52, hour-by-hour output results were calculated over the month of July, producing an overall distribution for each of the output parameters. Since only the indoor heat load was necessary input in Table 9, indoor temperature and ventilation rates were dependent on one another and were solved simultaneously, given the energy balance equation (Equation 10) and the appropriate wind and buoyancy-driven ventilation rate equation derived from the current study (Table 7). Within this calculation, the wind-driven ventilation component took into account the local environment and building orientation that was input by the designer, by determining the 83 corrected local wind velocity (Table 6), and the windward ventilation component perpendicular to the building (Section 4.6), respectively. The relative humidity was calculated based on a mass balance of water vapor for the space, given the outdoor relative humidity and the occupant's exhalation rate, detailed in Appendix A.2. The percentage of persons dissatisfied was calculated based on the set of thermal comfort equations in Appendix A.3. This tool calculated the output parameters for both the single and upper/lower opening geometries. The results are arranged in such a way as to allow for direct comparison. These results are shown in Figure 53, Figure 54, Figure 55, and Figure 56, for indoor air temperature, indoor relative humidity, air change rate, and percentage of persons dissatisfied, respectively. 30 thermal comfort zone 25 20 15 10 16-18 18-20 20-22 22-24 24-26 26-28 28-30 30-32 32-34 34-36 36-38 Indoor Air Temperature (C) u-Single Opening E Upper/Lower Opening Figure 53: Distribution of indoor air temperature for student room design in Cambridge, MA 84 25 thermal comfort zone 20 15 10- II 5 0 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 Relative Humidity (%) E Single Opening 0 Upper/Lower Opening Figure 54: Distribution of indoor relative humidity for student room design in Cambridge, MA 80 70 60 50 40 30 20 - 10 0 4-6 6-8 I1 8-10 10-12 II-12-14 14-16 16-18 18-20 ACH (1/hour) E Single Opening E Upper/Lower Opening Figure 55: Distribution of air change rate for student room design in Cambridge, MA 85 60 50 40 30 T 20 10 0-5 5-10 10-20 20-40 40-60 60-80 80-90 90-95 95-100 Percentage of Persons Dissatisfied (PPD, %) -] Single Opening N Upper/Lower Opening Figure 56: Distribution of percentage of persons dissatisfied (PPD) for student room design in Cambridge, MA 5.2.4 Discussion Based on the results in the above section, indoor conditions resulting from this single-sided ventilation design can clearly be seen and analyzed. For the month of July in Boston, the student rooms within this MIT residence building provide an effective natural ventilation environment for some percentage of the time, but fail to be effective at other times. For the parameter of indoor temperature, Figure 53 shows the distribution for both a single and upper/lower opening geometry. An indication of the thermal comfort zone limit is present on the chart to understand the level of comfort that is attainable with this design. The limit of the ASHRAE thermal comfort zone is generally 26-27oC, although in the chart the limit is extended to 28C, since natural ventilation usually allows for slightly higher temperatures and humidities where the natural breezes are assumed to create a more tolerable environment. However, even with this temperature value as the upper limit for indoor conditions, the single opening room produces temperatures outside the thermal comfort zone 40% of the hours in July. At the same time, the upper/lower opening room conditions are outside this range only 23% of the time, producing much better indoor comfort conditions. For the parameter of relative humidity, Figure 54 shows the distribution for both window geometries and also indicates the limit of the thermal comfort zone at 70%. Although, the generally accepted limit from ASHRAE is 60%, natural ventilation allows for a bit higher humidity conditions. Given this limit, 30% of the hours in July were above the limit for the single opening room, while 38% were above the limit for the upper/lower opening room. Indoor relative humidity conditions are dependent on the ventilation rate, which brings the humidity of the outside air into a space at a certain rate. Since upper/lower window geometries generally produce higher ventilation rates, a favorable condition, this at the same time brings more humid air into the space, which is clearly unfavorable. However, the difference in relative humidities between the two geometries is much less than the difference in indoor temperatures, which proves to be highly unfavorable natural ventilation conditions for the single opening geometry space. 86 For the parameter of ventilation rate, Figure 55 shows the distributions for the two window geometries, which barely overlap one another. The range of ventilation rates for the upper/lower window geometry peaks at the range of 10-12 ACH, while that of the single opening peaks only at the 4-6 ACH range. This indicates clearly that a room with an upper and lower opening can achieve ventilation rates that are approximately 6 ACH higher than that of a room with a single opening. This difference is a significant amount, and should therefore be considered. Finally, the parameter of percentage of persons dissatisfied (PPD) was determined in Figure 56, which shows this distribution for the two window geometries. For this parameter, only the positive range of the predicted mean vote scale (PMV) was considered (see Appendix A.3) since negative PMV is an indication of cold discomfort and is therefore not an issues in summer weather, when occupants always have the choice to close their windows. Negative values of PMV were therefore converted to PMV=0. The generally acceptable range of PPD in the building industry is at or below 25% PPD. From the figure, it is clear that the upper/lower opening geometry performs far better than the single opening geometry, as is seen mostly in the 0-5% PPD range. The majority of hours in the month of July fall within the lowest (0-5%) and highest (95-100%) ranges of the PPD spectrum, with both window geometries producing a substantial percentage of July hours in the range of 95-100% PPD. The upper/lower window geometry produced a 13% PPD frequency in this upper range, while the single opening geometry produced a 24% PPD frequency in this same range. 5.2.5 Conclusions From the above design tool and sample analysis, it has been shown that valuable information regarding the behavior of a particular single-sided ventilation space can be obtained. This information is laid out here in the form of bar charts, which indicate the distribution of indoor conditions for a particular design. From this format, the positive and negative aspects of a particular design can be obtained, so that further modifications can be made which target those indoor conditions that are unfavorable. For example, within the student rooms, the window geometry that has clearly shown to be more favorable is the upper and lower opening. This design for single-sided ventilation takes advantage of the vertical buoyancy effect associated with this strategy by creating openings where the inlet and outlet are separated by a large height difference. Maximizing the height difference between inflow and outflow has a significant impact on the conditions within a single-sided space, which has been demonstrated in the literature [35]. A negative aspect of the upper and lower opening room that could be seen from the results was the high relative humidity values that were obtained for 38% of July. By targeting this particular parameter as the problematic source, further design revisions can be made to address this problem. Perhaps introducing some low-humidity mechanical cooling into the space would reduce some of the influx of humid outdoor air. Overall, this tool can help designers to make relatively quick decisions regarding a particular idea, without the need for complicated analysis. Incorporating the results from analytical, empirical, and CFD models into one tool simplifies the design process. Time-consuming experiments are not required, and CFD models and other calculations for various design concepts are not necessary to obtain a basic understanding of particular design. The level of analysis that is desired by designers calls for a tool such as this one. A sample of this computer design tool, set up with hourly TMY data for July in Boston, is attached to this research study on floppy disk. This simplified version allows users to input their design and obtain hourly output, as well as a simple table of average output values over the month's period. The hourly output data for the indoor parameters can then be further analyzed in order to observe parameter distributions over the month. 87 5.3 Single-sided Ventilation General Design Guidelines The following section was created as a set of general guidelines for designers in order to help them in designing for optimum single-sided ventilation. These guidelines were set up to function separately from the rest of this study, in that the most important aspects of single-sided ventilation analysis have been extracted from this study and laid out in a step-by-step format. The guidelines require the user to obtain relevant information regarding single-sided ventilation rates from charts rather than equations, and include a sample case at the end for reference. 88 SINGLE-SIDED VENTILATION GENERAL DESIGN GUIDELINES The major driving forces of single-sided ventilation are: Temperature or buoyancy Wind - - Single-sided ventilation depends on the interaction of these parameters, which creates pressure differences across the openings(s), driving the air inside/outside the ventilated space. These forces must be accounted for when designing a space with natural ventilation strategies in mind. To allow for a set of simple design guidelines to be developed, simplified theoretical, analytical, and empirical solutions are used. Assumptions are made along the way, which are considered to be appropriate for this level of analysis. Temperature (Buoyancy) driven ventilation A major driving force in single-sided ventilation is the temperature difference between the indoor and outdoor environments. This temperature force is called buoyancy or stack-driven flow. A temperature difference between a space and the environment causes a density difference, where the warm air is less dense than the colder air. As a result, a pressure difference occurs between the inside and outside air. The higher internal pressure at an upper opening drives outflow and the lower internal pressure at a bottom opening drives inflow. The flow is especially evident for a space with (1) an upper and lower opening or (2) a single large opening, shown in Figure DG la and b, respectively. The following guidelines have therefore been established based on single opening and upper/lower opening geometries. (b) (a) Figure DG 1: Buoyancy-driven flow through (a) an upper and lower opening, (b) a single opening Compared with an upper and lower opening geometry, a single large opening generates lower ventilation rates and the ventilated air does not penetrate as far into the space. Single sided ventilation is effective to a depth of about: - 2.5 times the floor to ceiling height for an upper/lower opening geometry (Figure DG 2) 2 times the floor to ceiling height for a single opening geometry (Figure DG 3) 89 This effective depth is a measure of the extent of fresh outdoor air penetration into single-sided naturally ventilated buildings. Therefore, the room that is designed should not exceed the effective depth in order to maintain acceptable thermal comfort and good air quality. However, if this criterion cannot be met, ceiling fans or a similar type of mechanical assistance may be used to augment the effective depth of fresh air, allowing the space to be deeper if necessary. W:5 2-5H h ox H W Figure DG 2: Single-sided ventilation with an Il ItU_ upper/lower opening [381 MAVISP: W 1; 2H H .11 I W Figure DG 3: Single-sided ventilation with a single opening 1381 Stronger airflow will be induced when there is a large vertical separation between inlets and outlets, and when there is a large difference between indoor and outdoor temperatures. As inside and outside temperatures equalize, the stack effect approaches zero and there is no driving force for ventilation. The most important parameter for natural ventilation design is the volume flow rate through the opening(s). For buoyancy-driven single-sided ventilation through an upper and lower opening (Figure DG I a) of equal area, A (M 2 ), this volume flow rate is approximated in Figure DG 4 for a range of h values, where h is the height between the centers of each window. 90 0.6 -- -h=2.5m 0.5 h=2.Om -- 0. E -h=0.5m 0.2 0.1 .- 0~ 0 2 4 6 A T (Tinside-Toutside, C) h=0.5m ------------ h=1 m -- --- h=1.5m 8 h=2m 10 h=2.5m Figure DG 4: Buoyancy-driven ventilation rates per unit area for an upper/lower opening geometry [101 The volume flow rate is given per unit area, V/A, and must therefore be multiplied by the appropriate window area, A, in order to derive the ventilation rate in units of m3/s. For the case where the areas of the upper and lower windows are different, the area in the V/A term must be replaced by A * (M 2 ), defined as [12] A* =[,fA, A/(At 2 +Ab 2 )] (DG-1) For a single large opening (Figure DG lb) of area, A (m 2 ), the volume flow rate is similarly approximated in Figure DG 5 for a range of h values, where h is the height of the window [13]. 0.18 0.16 0.14 h=2.Om h=1.6m 0.12 E 0.10 0.08 0.06 - h=1.2m ------------------------------h =0 .8 m h=0.4m - 0.04 0.02 ---- 0.00 0 2 4 6 Delta T (Tinside-Toutside, C) h=0.4m h=1.6m ------------- h=0.8m h=2.Om 8 10 ------- h=1.2m Figure DG 5: Buoyancy-driven ventilation rates per unit area for a single opening geometry 1131 91 Wind driven ventilation Single-sided natural ventilation relies on pressure differences across its openings to drive air inside and outside a particular space. The related physical processes are very complex, especially for the case of wind-driven flow. This is due to the variability of the outdoor wind conditions and due to the turbulent motion of the wind. The results of a simple empirical model developed for wind-driven flow are shown in Figure DG 6. This figure plots the volume flow rates for wind-driven flow through an upper and lower opening, each of area, A (M 2 ), and through a single opening of area, A (M 2 ). This figure assumes the directed wind is perpendicular to the building facade. A correction factor will be added to this ventilation rate in the next section to account for wind direction. If the window areas for the upper/lower opening case are different, an average area of the upper and lower opening, Aag, can be used. 0.8 0 .7 - ---- 0.6 u 0.5 Upper/Lower Opening 0.4 -> 0.3 0.2 - 0.1 -Single Opening 0.0 0 2 4 6 8 Viocal, Local Wind Speed (m/s) Upper/Lower Opening - -- Single Opening Figure DG 6: Wind-driven ventilation rates for an upper/lower and single opening geometry 1231 If the local wind speed at the site of a particular building is not known, the following conversion can be applied to determine the site velocity for a particular local environment. Viocaiz = KVmeza (DG-2) where V,,,, (m/s) is the meteorological wind speed (at a nearby weather station), and K and a are constants given in Table DG 1 for different local environments. The variable, Z, represents the height along the building of the particular space being studied. The average meteorological wind speed and wind direction for a particular location should be selected. To evaluate an overall ventilation rate for the rooms along the entire facade of a building, setting z to be half the height of the building will be appropriate in obtaining an average value. 92 Table DG 1: Values of coefficients for Vioca=,zKVmetZa under local environment conditions 1101 Nature of terrain Open flat country Country with scattered wind breaks K 0.68 0.52 a 0.17 0.20 Urban City 0.35 0.21 0.25 0.33 Wind and Stack The separate stack effect and wind effect determined in this study are found to combine with one another in the following manner. Vtotal = VI(stack )2 + (Vwind cos 0)2 (m 3 /s) (DG-3) where 0 is the angle between the meteorological wind speed direction and the direction perpendicular to the building fagade. The (cosG) term has been included since the wind speed will not always be directed perpendicular to the single-sided facade. However, if you wish to evaluate the design for perpendicular winds only (generally the optimum condition), this term can be ignored. The relation in Equation 3 produces the total volume flow rate for single-sided ventilation. In order to translate this volume flow rate into an equivalent air change rate, the following conversion is applied. (DG-4) ACH = V -3600 V where _1(m 3 ) is the volume of the space. The following section applies the concepts of these guidelines in order to analyze the potential ventilation rates of a particular space. These set of guidelines will be valuable in evaluating proposed designs and for making recommendations on necessary modifications. Worked Example - MIT Student Residence 2002 (Steven Holl Architects) To analyze single-sided ventilation design for the city of Cambridge, Massachusetts, a student residence building currently being constructed on the MIT campus and designed by Steven Holl Architects, was analyzed for its single student room geometry. The geometry of this room, along with its the environmental conditions, is shown in Figure DG 7. For purposes of this example, and in order to produce realistic estimates, an average outdoor temperature of 23'C was assumed, along with an indoor air temperature of 25'C, creating a AT of 2'C. The calculation was performed for a south facing facade. An average meteorological wind speed of 4 m/s and 0 value of 450 (i.e., wind is directed from the southeast) was assumed based on typical Boston weather data. 93 t=23'C Vmet= 4 m/s 450 Awmdc s; 0.4 n ~1~ T2 15 0 C V= 38.2 n 3 H = 2.8 m ZbUilding=30 m h =2 M 0.4 m2 - W = 4.7tn Figure DG 7: Single student room geometry with environmental conditions for moderate seasons Initially, the space was confirmed to be designed at an allowable depth of 4.7 m (for effective depth of fresh air purposes), only 1.7 times the floor to ceiling height. Then, from the information given in Figure DG 7, an analysis was performed to determine the average ventilation rates capable of being produced by this design in this particular environment. The ventilation rate due to stack effect was found to be = 0.22m / s stack A Ystack (Figure DG 4) = (0.22m /s)(0.4m 2 ) = 0.088 m3 /s = 8.29 ACH The ventilation rate due to wind effect was found by first determining Vloca based on the assumed local environment of a city. Vl0 ca was evaluated at half the height of the building, 15 m. Viocali 5 = (0.21)(4)(15)"' Vioca,1 5 = 2.05 (Equation DG-2) m/s The ventilation rate due to wind effect was then found to be ind = A 0.2m/s (Figure DG 6) *VWnd = (0.2m /s)(0.4m 2 ) = 0.08m 3 /s = 7.54ACH The total ventilation rate due to both stack and wind effect is given by (0.088)2 + (0.08 cos(450)) *total = Vtotai =0.105m 3 /s = 9.86ACH 2 (Equation DG-3) An ACH of 9.86 provides optimal ventilation for single-sided ventilation applications, which generally produces air change rates more typically in the range of 5 ACH (considerably lower than that of cross 94 ventilation). If the previous calculation was performed for a corresponding single opening equal in size to the total area of both the upper and lower openings (a 0.9 m W x 0.9 m H opening), for the same geometry and environmental conditions, this setup would produce an air change rate of 4.7 ACH. Therefore, the upper and lower geometry opening for single-sided ventilation greatly increases the ventilation potential over that of a single opening. Based on the above analysis, natural ventilation has been determined to be a beneficial strategy for the single student rooms during the moderate seasons. The rooms are well designed in providing for this energy efficient strategy. 95 5.4 Conclusions In order to devise a set of rules for predicting airflow in the case of single-sided ventilation, a computer design tool and a set of general guidelines have been established. With the help of these two tools, designers are now able to assess their designs for ventilation performance and make any necessary modifications in a relatively simple, straightforward manner. This is valuable to development of natural ventilation design, especially in the field of single-sided ventilation, since this strategy will always be present due to typical building layouts, and must therefore be addresses. The potential for natural ventilation in these spaces has proven to be great, and should therefore be utilized in the best way possible. 96 CHAPTER 6: CONCLUSIONS, RECOMMENDATIONS, AND FUTURE WORK 6.1 Conclusions Natural ventilation is a critical strategy in the move towards energy efficient building design. In order for this strategy to be most effective, the interaction of natural and built forces must be determined. Singlesided ventilation is a significant type of natural ventilation, especially since single-sided building forms are so prevalent, especially in the US. It is therefore necessary that the physical behavior of this ventilation method be well understood. Unfortunately, single-sided ventilation has been given far less attention in the building research and design field than other forms of ventilation, such as cross ventilation. This is in part due to the fact that the complicated effects of the natural forces of temperature and wind on the indoor single-sided environment lack a full understanding, making predictions of airflow difficult to correctly determine. Analytical, experimental, and numerical studies have been performed in the field of single-sided ventilation to help provide information on the physical flow characteristics for this ventilation strategy. For buoyancy-driven flow, well-established semi-analytical solutions have been developed to determine ventilation rates. For wind-driven flow, empirical models have been developed based on detailed experiments. These will be critical studies for comparison purposes with current findings. CFD modeling is a very useful tool in natural ventilation design. It enables designers to analyze various different designs and evaluate the abilities of these designs before beginning actual implementation of them. However, since CFD has used some approximations to determine the flow, it is also very important therefore to ensure that it is applied accurately. This is especially true for the case of natural ventilation, which is characterized by unpredictable and complicated airflow patterns and presents a challenge to the field of CFD modeling. The CFD tool has therefore been validated solely for the purpose of natural ventilation studies. The performance of CFD for these validation cases has been very good and promising overall. For indoor flow, CFD was able to accurately predict air temperature and concentration distributions throughout a room with mechanical displacement ventilation. Verifying the temperature and concentration fields for such an environment, although it is mechanically ventilated and not naturally ventilated, is very significant because displacement ventilation and single-sided ventilation are based on the same physical buoyancy and airflow principles. When performing a CFD validation on outdoor airflow around a bluff body, the pressure coefficient results from CFD were found to agree well with the experimental measurements. CFD was shown, however, to underpredict the recirculation zone on top of the block, which is not believed to impact its intended applications towards single-sided ventilation. A similar validation was then performed, which included the indoor and outdoor environment for singlesided ventilation. For this case, velocity distributions were compared along the streamwise direction of flow. An excellent agreement was found in velocity distributions along the windward and indoor sections of the building model. However, the computational results for the leeward velocity distributions did not agree well with the experimental data. This inability of CFD to accurately model the recirculation zone on the leeward section of a building will therefore have an impact on the study of single-sided natural ventilation in this location. After detailed validation cases were performed, the various design features of single-sided natural ventilation were then explored and analyzed in order to gain a better understanding of the complexities and characteristics of single-sided ventilation. Based on results from analytical, empirical, and CFD models, trends and design issues were revealed. CFD models were then applied further to develop results for single-sided ventilation in areas that are currently lacking in research. Although these areas could not 97 be validated, they provided an overall background study into areas of natural ventilation that have a huge potential for future work. The first part of the study focused on the buoyancy and wind-driven effects of single-sided ventilation. For buoyancy-driven ventilation, CFD models were established in order to determine the appropriate modeling setup for this highly sensitive temperature-driven flow. Upon detailed analysis, it was found that modeling both the outdoor and indoor environment is necessary for correct airflow and temperature results within CFD. For this combined stack model, ventilation rate results were found to agree with semi-analytical solutions for buoyancy-driven flow, within 10%. This agreement was found to exist over a range of indoor temperature conditions and for different window configurations. The modeling of the outdoor environment produced consistent results with analytical solutions, as well as providing information on the interaction between the indoor and outdoor environment, valuable information that cannot be obtained from an analytical equation or from solving only the indoor computational domain. The wind and buoyancy-driven effects of single-sided ventilation were then investigated with an appropriate CFD model, which calculated ventilation rates over a range of wind speeds. These results were compared with two empirical models from the literature, which were both based on a single opening setup for single-sided ventilation. The two models were very similar, and upon comparing these models with CFD results, the CFD model was found to follow the same trends, but consistently underestimate the ventilation rates by 25%. This source of difference between the CFD and empirical models is believed to be due to the fact that the RANS modeling technique within CFD solves for averaged flow parameters, whereas the ventilation rate for single-sided ventilation is largely dependent on time-varying air fluctuations at the interface of the opening, which create turbulence, a major driving force in single-sided ventilation. Based on the performance of CFD within the validated cases, CFD models were applied further in areas where empirical and analytical models have not been established. First, CFD model results for an upper and lower window geometry were used to develop curve-fit equations for ventilation rates through this type of opening geometry. The ventilation rates found for the upper and lower opening geometry were found to be about twice that of the single opening geometry, clearly showing the advantage of the former window design over the latter for single-sided ventilation. Further studies were also performed on the effects of wind direction, counteracting effects of wind and buoyancy, and options for mixed-mode ventilation. Although these results could not be validated, the confidence built into CFD modeling of single-sided ventilation over the course of this study has warranted further analysis of this natural ventilation strategy. From these additional research areas, several conclusions were made. For wind direction studies, a curve for ventilation rates versus wind direction was determined. However, since the use of outdoor CFD modeling has encountered problems in modeling the leeward region of a building, there was a lack of validation in the results obtained on this part of the building. Therefore, only the results found along the windward side were used for further analysis. This ventilation rate curve followed an approximate path of cos o. In another brief study, attention was drawn to the counteracting wind and stack effect that occurred on the middle-level room of the wind and stack CFD model, where the wind forces drove air in through the upper opening and out through the lower opening. This was verified by tracking the velocity patterns through the room at various wind speeds. At some wind speed in the middle of this range, a minimum ventilation rate occurred, designating the point at which the wind and buoyancy forces were approximately equal and flow reversed direction. No guiding rules could be established for predicting the occurrence of counteracting wind and stack effect, since no consistent trends were observed, but further research is recommended. 98 Mixed-mode ventilation options were also looked into as possible modifications to single-sided ventilation designs that do not provide sufficiently favorable indoor conditions. The two types of mixed mode systems analyzed were a low cooling displacement ventilation (combined with natural ventilation) system, and a cross ventilation duct system. Both systems improved conditions within the space by decreasing the overall indoor temperature, in the case of the displacement ventilation system, or by increasing the ventilation rates through the spaces, in the case of the duct cross ventilation system. These systems, however, also created additional airflow and temperature issues in the process that needed addressing. This is a valuable, new field of natural ventilation that needs a great deal of further research in the future and can have a large impact on the field of energy-efficient building design. In order to devise a set of rules for predicting airflow in the case of single-sided ventilation, a computer design tool and a set of general guidelines was finally established. With the help of these two tools, designers are now able to assess their designs for ventilation performance and make any necessary modifications in a relatively simple, straightforward manner. This is valuable to development of natural ventilation design, especially in the field of single-sided ventilation, since this strategy will always be present due to typical building layouts, and must therefore be addressed. The potential for single-sided ventilation has proven to be significant - this natural ventilation strategy should therefore be utilized in the best way possible. 6.2 Limitations of the Study and Future Recommendations Within this complete study, a broad range of areas has been explored pertaining to single-sided natural ventilation. During the process, various obstacles in the analysis presented themselves and were addressed here in the study. Although the study attempts to make conclusive results at each step along the way, certain issues could not be resolved and certain limitations in the study therefore exist. This study attempts to utilize the various tools available, including analytical, experimental, and computational tools, in order to fully understand the process of single-sided ventilation in order to design for a better, more energy efficient building. However, each of these tools requires assumptions, thereby limiting the confidence in and accuracy of the particular tool. Semi-analytical equations were used for the purpose of determining ventilation rates for buoyancy-driven flow. Although these equations are widely used in the field of natural ventilation, the simplicity that is inherent in these tools requires certain assumptions that may not represent the physical situation. For the case of buoyancy-driven flow, the semi-analytical equations assume a constant indoor temperature. This assumption would be an appropriate assumption for the case of mixing ventilation, but not for displacement ventilation, the principles upon which single-sided ventilation is based. Current work is being performed on more complex equations that account for more than one temperature zone within a space. These tools are not widely applied, however, and many times are only appropriate for specific cases. Future work in developing a more accurate analytical model for buoyancy-driven single-sided ventilation flow would be very useful. Empirical models were also used in this study to analyze the effects of wind and combined-driven flow on single-sided natural ventilation. However, the detailed empirical model of Phaff and deGids was based on the lowest level apartment of a space within an urban environment with a specific window geometry and size. These features place large constraints on a general study of single-sided ventilation, since the results only apply to a specific case. However, this empirical model was found to agree well with another model from the literature, which was applicable for single-sided ventilation cases through a single window - this similarity between both empirical models in turn strengthened each other's cases. At the same time, certain issues were not addressed within these empirical models. One of these issues is the variation of 99 ventilation rates along the facade, especially along the height of the facade. Another issue was the variation of ventilation rate with wind direction. This latter issue is especially important since the wind is rarely directed perpendicular to the facade. Although the current study performed an analysis ID determine where along a building the wind and buoyancy forces oppose and strengthen each other, no consistent pattern could be found. The negative impact that these opposing wind and buoyancy forces have on the ventilation through certain spaces needs to be addressed further. Another aspect of single-sided ventilation that requires more research is the impact that wind direction has on ventilation rates. Much research has been done in this area for the case of cross ventilation, and well-established rules have been drawn up. However, studies on wind direction effects need to be extended to the case of single-sided ventilation. A third tool used during this study, perhaps the most important tool, was computational fluid dynamics (CFD). The type of CFD technique that was used in this study was that of Reynolds averaged NavierStokes (RANS) modeling. RANS is the most commonly used form of CFD modeling that is currently used, partially due to the fact that the computational burden associated with it is less than that of other CFD techniques. RANS modeling therefore has a great current and future potential use in the building technology industry. For the case of natural ventilation, issues have been raised on the ability of this timeaveraging computational technique to model the unpredictable, fluctuating airflows that are characteristic of natural ventilation. A goal of this study was therefore to determine how well RANS CFD modeling performed for single-sided natural ventilation. This was especially important since the application of natural ventilation for single-sided cases in particular is poorly understood, partly due to the fact that this flow is especially dependent on fluctuating airflow. Within the study, the inability of RANS modeling to fully capture fluctuating, instantaneous flow was confirmed for the case of wind-driven flow, where CFD was found to underpredict empirical model results by approximately 25%. This limitation of RANS computation modeling must be accounted for when performing analyses on natural ventilation. Another weakness of RANS modeling, revealed through outdoor CFD validation, was the inability of RANS to model the separation region on the roof of a building, along with its overestimation of the recirculation zone behind a building. The former problem is not believed to present itself for the application of natural ventilation. However, the latter problem becomes a significant issue when analyzing apartments with single-sided ventilation on the leeward side of a building. Upon completion of this single-sided natural ventilation study, a computer design tool and a set of general guidelines were developed in order to compile the complete research work into a cohesive, easy-to-use form. The computer tool outputs several indoor parameters to enable designers to analyze their designs and make possible improvements. A possible area of future work that would be beneficial is to develop this tool further to give more output information and possible recommendations on modifications. Finding a way in which to provide the user with information regarding energy savings of a particular natural ventilation design over another, or as compared with air conditioning, would be very helpful. Also, based on the results, a set of recommendations can be made. For example, if the ventilation rates are low but the temperature conditions are within the thermal comfort zone, suggestions on ways in which to maximize this ventilation rate should be made, such as designing an upper and lower window system for the space that maximizes the height between these windows, or by going even further to suggest installing a cross ventilation duct system into the building to greatly increase these ventilation rates. However, if the ventilation rates are low and the temperature conditions are above the thermal comfort zone, increasing the ventilation rate will not be favorable. Under these conditions, complete natural ventilation may not be advisable, and some form of low cooling mixed-mode ventilation may be necessary to recommend. The set of general guidelines established at the end of this study aim to help the designer in understanding the potential ventilation rates that are possible with a particular design. However, in order to do this, the guidelines are simplified to only one set of inputs, and therefore only one set of outputs. This tool therefore has a limited capability since it is difficult to choose one typical outdoor temperature, wind 100 speed, and wind direction to evaluate a particular design that will be subject to large variations in these conditions throughout the course of the year. It is first step, however, in the design process, enabling the architect to compare natural ventilation performances of their various design options. 101 REFERENCES 1. Energy Information Administration. "State Energy Data Report 1995." Tables 3 through 7. 2. J.F. Busch. "A Tale of Two Populations: Thermal Comfort in Air-conditioned and Naturally Ventilated Offices in Thailand." Energy and Buildings 18 (3-4) 1992: 235-49. 3. R. Zhao and Y. Xia. "Effective Non-isothermal and Intermittent Air Movement on Human Thermal Responses." Proc. of Roomvent 98 2 1998, Stockholm. 351-57. 4. J.J. Finnegan, C.A.C. Pickering, and P.S. Burge. "The sick building syndrome: prevalence studies." British Medical Journal 289 1994: 1573-75. 5. Energy Consumption Guide 19. "Energy efficiency in offices." London: Energy Efficiency Office/HMSO 1993. 6. R. Ellis. "The British office market - the workplace of tomorrow; the consumer's view." 1994. 7. E. Dascalaki, M. Santamouris, and D.N. Asimakopoulos. "On the use of deterministic and intelligent techniques to predict the air velocity distribution on external openings in single-sided natural ventilation configurations." Solar Energy 66 (3) 1999: 223-43. 8. P.F. Linden. "The fluid mechanics of natural ventilation."Annual Review of Fluid Mechanics 31 1999: 201-38. 9. F. Allard, "Natural Ventilation in Buildings: A Design Handbook." London: James & James Ltd, 1998. 10. D. Etheridge and M. Sandberg. "Building Ventilation: Theory and Measurement." Chichester, England: John Wiley and Sons, 1996. 11. W.G. Brown and K.R. Solvason. "Natural convection through rectangular openings in partitions- I vertical partition." International Journal of Heat and Mass Transfer 5 1962: 859-65. 12. Yuguo Li. "Buoyancy-driven natural ventilation in a thermally stratified one-zone building." Building and Environment 35 2000: 207-14. 13. H.B. Awbi. "Air movement in naturally-ventilated buildings." The University of Reading, Department of Construction Management & Engineering, WREC 1996. 14. D.E. Kiel, and D.J. Wilson. "Gravity driven flows though open doors." 7t AIVC Conference, September 29, 1986, Stratford on Avon, UK. 15. J. Clarke. "Manual of ESP." Glasgow, UK: University of Strathclyde, 1993. 16. G. Walton. "AIRNET, A computer program for building airflow network modeling." MISTR 894072, National Institute of Standards and Technology, 1988. 17. H.E. Feustel, F. Allard, V.B. Dorer, E. Garcia Rodriguez, M.K.Herrlin, L. Mingsheng, H.C. Phaff, Y. Utsumi and H. Yoshino. "Fundamentals of the multizone air flow model- COMIS." Tech. Note AIVC 29. Coventry, UK: International Energy Agency, Air Infiltration and Ventilation Centre, 1990. 18. M. Santamouris. "NORMA, A simplified model for passive cooling." Manual, written by P. Kelly, Zephyr Architectural Competition, University College, Dublin, 1994. 19. B.R.E. "Manual of Breeze." Watford, UK: Building Research Establishment, Garston, 1992. 20. E. Dascalaki and M. Santamouris. "Manual of PASSPORT-AIR, Final Report." PASCOOL Research Program, European Commission, D.G. XII, 1995. 21. J.P. Cockroft and P. Robertson. "Ventilation of an enclosure through a single opening." Building and Environment 11 1976: 29-35. 22. E. Dascalaki, E., M. Santamouris, A. Argiriou, C. Helmis, and D.N. Asimakopoulos. "On the combination of air velocity and flow measurements in single sided natural ventilation configurations." Energy and Building 24 1996: 155-65. 23. BS 5925: 1991. "Code of practice for ventilation principles and designing for natural ventilation." British Standards Institute 1991. 102 24. J.C. Phaff, W.F.de Gids, J.A. Ton, D.V. van der Ree, and L.L.M. Schijndel. "The ventilation of buildings: Investigation of the consequences of opening one window on the internal climate of a room." Report C 448. Delft, Netherlands: TNO Institute for Environmental Hygiene and Health Technology (IMG-TNO), March 1980. 25. S. Chandra, P. Fairey, and M. Houston. "A handbook for designing ventilated buildings." FSEC-CR26. 27. 28. 29. 93-83, Cape Canaveral, Florida: Florida Solar Energy Center, 1983. Phaff, H. Personal Communication, August 9, 2000. F. Allard (ed). "Single sided ventilation." Chapter 2, Brussels: PASCOOL Research Project, MDS/VTL Final Report, EC DG XII, 1995. Q. Chen. "Comparison of different k-e models for indoor airflow computations." Numerical Heat Transfer 28 (B) 1995: 353-69. Q. Chen. "Prediction of room air motion by Reynolds-stress models." Building and Environment 31 (3) 1996: 233-44. 30. V. Yakhot, S.A. Orzag, S. Thangam, T.B. Gatski, and C.G. Speziak. "Development of turbulence models for shear flows by a double expansion technique." Physics Fluids A 4 1992: 1510-20. 31. D. Lakehal and W. Rodi. "Calculation of the flow past a surface-mounted cube with two-layer turbulence models." J. Wind Eng. Ind. Aerodyn. 67/68 1997: 65-78. 32. S. Murakami. "Overview of turbulence models applied in CWE-1997." J. Wind Eng. Ind. Aerodyn 74-76 1998: 1-24. 33. S.J. Emmerich and K.B. McGrattan. "Application of a Large Eddy Simulation Model to Study Room Airflow." ASHRAE Transactions 104 1998: 1128-40. 34. A.J. Schaelin, A. J. van der Maas, and A. Moser. "Simulation of Airflow through Large Openings in Buildings." ASHRAE Transactions 98 (2) 1992: 319-28. 35. K. Li and S.L. Teh. "Two-dimensional numerical study of airflow through large openings." Proc. Indoor Air '96, 2, July 21-26, 1996, Nagoya, Japan, 1027-32. Gan. "Effective depth of fresh air distribution in rooms with single-sided natural ventilation." 36. G. Energy and Buildings 31 2000: 65-73. 37. R.H. Reed. "Design of Natural Ventilation in Hot Humid Weather, Housing and Building in Hot Humid and Hot Dry Climates." Building Research Institute, National Research Council, Washington, DC, USA. http://fridge.arch.uwa.edu.au/topics/thermal/airflow/ventilation.html, 1953. 38. CIBSE Applications Manual AM10: "Natural ventilation in non-domestic buildings." London: The Chartered Institution of Building Services Engineers, 1997. 39. A. D. Arens. "Evaluation of Displacement Ventilation for Use in High-Ceiling Facilities." Massachusetts Institute of Technology Master of Science in Mechanical Engineering Thesis, June 2000. 40. AIJ Working Group. "Numerical Prediction of Wind Loading on Buildings and Structures." Division for Wind Loading Design, Architecture Institute of Japan, (in Japanese), 1994. 41. ASHRAE Handbook, 1997 Fundamentals. American Society of Heating, Refrigerating and AirConditioning Engineers, Inc., Atlanta GA, 1997. 42. Yi Jiang, Don K. Alexander, Huw Jenkins, Rob Arthur, and Qingyan Chen. "Natural ventilation in buildings: measurement in a wind tunnel and numerical simulation with large eddy simulation." paper in progress, May 2001. 43. Steven Holl Architects. "Undergraduate Residence 2001, MIT, Cambridge, Massachusetts." November 2, 2000. <http://www.stevenholl.com/pages/mit.html> 44. W. Marion and K. Urban. "User's Manual for TMY 2 Typical Meteorological Years." Derived from the 1961-1990 National Solar Radiation Data Base, June 1995. 45. D. Bienfait, L. Vandaele, J. van der Maas, and R. Walker. "Single-sided ventilation." Proceedings of the 12th AIVC Conference, 24-27 September, 1991, Ottawa, 1:73-98. 103 46. D.W. Etheridge, P.H. Kemp. "Measurements of Turbulent Flow Downstream of a Rearward-Facing Step." Journal of Fluid Mechanics 86 (3) 1978: 545-66. 47. Muriel Regard-Alchakkif, Francois-Remi Carrie, Gerard Guarracino. "Natural ventilation of a room through a large external opening: calculation using a CFD code." Rev Gen Therm, (in French) 37 1997, 137-47. 48. R. Chang. Duct Analysis for Student Residence Building design by Steven Holl Architects. Building Technology Program, MIT, May 2001. 104 APPENDIX A: DETAILED CALCULATIONS A. 1 Single Opening Volume Flow Rate Derivation [12] The pressure difference due to temperature difference across a large opening is: (A-1) Ap(z) = Apgz where Ap is the difference in density across the opening, z, is the height, and g is the acceleration of gravity. Also, v(z)= (A-2) 2Ap(z)/ p Therefore, u(z) C v(z) =( Vmax z 112 and (A-3) (h/ The mean velocity (V) through an opening of height (h) is: - Umax zl12dz = V=h' 2 2 2 fh2 3 h 3/2 Vmax (A-4) 3 hv max The volume flow rate through the opening, V, is: 2 Vstack = Cd v= 2 - C whv 3 (A-5) = -Cd Aux 3 where w is the width of the opening. However, in a buoyancy-driven flow, the equal masses of air enter and leave through the same opening. If h is the total height of the opening, then the inflow and outflow is: Sd C 3 (A-6) Av max From Equations A-1 and A-2, together with the approximation in Equation 3, it follows that: _CdA Vstack - A 3 gh AT (A-7) Tout where AT is the temperature difference across the opening. 105 A.2 Relative Humidity The relative humidity, p, was calculated based on a mass balance of water vapor for the space, given the outside relative humidity value and the indoor occupant's exhalation rate, cperson (55 g/hr or 1.528x10- 5 kg/s for an average person). rihwin +c person = iw (A-8) out where fii = mass flow rate (kg/s of air) cperson = exhalation rate of an average person (kg/s of water vapor) w i = humidity ratio entering space (kg water vapor/kg air) w = humidity ratio exiting space (kg water vapor/kg air) For purposes of the computer design tool, an average humidity ratio for the space was assumed to be W. avgspace +w W + InW 2 Cperson 2 From this average humidity ratio value and the indoor temperature value, relative humidity could be found according to the following equation [40] W avg,spacePa (A-10) 0.6219ps where pa=standard atmospheric pressure, 101039 Pa pj=saturation pressure, Pa The saturation pressure, pS, was calculated over the temperature range of 0 to 200C, from the following equation [Al], ln(ps)= C, /T +C2 +C 3 T+C 4 T2 +C 5 T3 +C 6 lnT (A-11) where C =-5.8002206E+03 C2=1.3914993E+00 C3 =-4.8640239E-02 C4=4.1764768E-05 C5=-1.4452093E-08 C6=6.5459673E+00 A.3 Percentage of Persons Dissatisfied Thermal comfort is a very important parameter in natural ventilation design that must be accounted for. A designer needs to predict the performance of a particular design based on thermal comfort levels. These comfort levels guide the designer in determining whether a particular indoor environment will be 106 satisfying to its occupants. The most important comfort parameters for natural ventilation design addressed so far has been indoor air temperature and ventilation rate. However, in reality, comfort is influenced by a number of factors, only two of which are indoor air temperature and ventilation rate. Other factors, such as temperature of the room surfaces, humidity, local air speed, type of clothing, and level of activity, are also significant to thermal comfort. In general, comfort occurs when body temperatures are held within narrow ranges, skin moisture is low, and the physiological effort of regulation is minimized [40]. All these parameters have been evaluated through a single variable, the predicted percentage of dissatisfied for thermal comfort (PPD), a widely used and accepted criteria to evaluate thermal comfort conditions. The predicted percent dissatisfied (PPD) is evaluated as [A2]: PPD = 100 - 95exp(-0.03353PMV 4 - 0.2179PMV 2 ) (A-12) In this equation, PMV, the predicted mean vote, predicts the mean response of a large group of people according to the ASHRAE thermal sensation scale shown below [40]. +3 +2 +1 0 -1 -2 hot warm slightly warm neutral slightly cool cool -3 cold Fanger [A3] related this PMV index to the imbalance between the actual heat flow from the body in a given environment and the heat flow required for optimum comfort at the specified activity by the following equation: (A-13) PMV = [0.303exp(-0.036M) + 0.028]L where the thermal load on the body, L, is the difference between the internal heat produced by the body and the heat lost to the environment through the processes of convection, radiation, and evaporation. L can be calculated as 4 L = M - W -{3.96x0-8 fe[(TC 1 +273)4 - (Tr + 273) ]+ fc h c(Tc - T) + 3.05x10 3 [5733 - 6.99(M - W) - Pa ]+ 0.42(M - W - 58.15) + 5 1.7x10- M(5867 - Pa) + 0.0014M(34 - T)} with M=metabolism (W) W=external work (W) f =cloth factor T=local air temperature (oC) Ta=cloth temperature (oC) T,=mean radiant temperature (oC) h =convective heat transfer coefficient between the cloth and air (W/nC) 107 (A-14) Pa=partial water vapor pressure (Pa) The terms, f , T1 ,and h are determined by the following equations: fC1 =1. 0 5 +0. 6 4 51 0.078 (A-15) for Id < 0.078 (A-16) for Id cd fc = 1.00 +1.2901cl Tci = 35.7 -0.028(M - W) - Ic {3.96x1T-afc[(Tc, + 273)4 - (Tr + 273)4] + fc1hc(Tc, - T)}(A-17) 0 5 h = 2.38(Tc, - T) for 2.38(Tc - T) .25 hC = 12.lu0 5 for 2.38(Tc, - T) .5 12.1u 05 <12.1u 0 5 (A-18) (A-19) where Id and u are the insulation clothing value and the local air velocity, respectively. For the PPD calculation in Equation A-12, dissatisfied is defined as an environment with a PMV value outside the range of -1<PMV<+l, or 5%<PPD<25%. The PMV-PPD model is widely used and accepted for design and field assessment of comfort conditions. These thermal comfort indices are used in the current study to analyze the conditions for potential indoor environment designs. A.4 Effective Depth of Fresh Air The effective depth of fresh air is a measure of the extent of fresh outdoor air penetration into a space. Effective distribution of fresh air within an occupied space is significant to the thermal comfort and indoor air quality of the space. In mechanically ventilated spaces, this variable can be controlled through the design of the air distribution system. However, since natural ventilation is less controllable than mechanical ventilation, the design of a maximum room depth for effective air distribution must be considered. This issue is especially important for the case of single-sided ventilation. Since the effective depth of fresh air is a measure of the extent of fresh outdoor air penetration into single-sided naturally ventilated buildings, the design room depth should not exceed the effective depth in order to maintain acceptable thermal comfort and good air quality. The effective depth for single-sided natural ventilation is most critical in summer when the ventilation rates are the lowest, but the required air change rates for maintaining thermal indoor comfort are the highest. The effective depth of fresh air for single-sided ventilation is the distance that fresh air travels from the inlet into the space. Along this path, the velocity component of the fresh air decreases to the room air velocity. The point at which the fresh air velocity decreases to this value is not easy to determine, especially in the case of buoyancy-induced natural ventilation, where the incoming air velocity tends to be low and may not be distinguishable from the room air movement. Sometimes, since the temperature distribution of the incoming air differs from that of the room air, their interface can be used as an indicator of the effective depth of fresh air. An alternative way in which to determine this depth is by first determining the local mean age of air. The local mean age of air is the average time it takes for air to travel from the inlet to any point in the room. This is a more relevant indicator of the effective depth of fresh air than the temperature distribution. The criterion for the local mean age of air is usually the nominal time constant, or the ratio of the air volume to the airflow rate, i.e. the reciprocal of the air change rate. In an experimental study performed on the effective depth of fresh air distribution, measurements were taken over a wide range of realistic conditions in several deep office spaces with single-sided ventilation [A4]. A distance equivalent to the effective depth was measured in terms of ihe local mean age of air. This effective depth is determined as the location at which the local mean age of air equals or is approximately equal to the nominal time constant, or the reciprocal of the air change rate (1/time). Any 108 location at which the local mean age of air starts to increase above this value designates areas in which fresh air is not being properly ventilated to, or locations of poor air quality. These results were used to determine the maximum room depth over which fresh air distribution would be effective. The effects of window location and partitions on air distribution and internal climate were also addressed. The results were used to provide information regarding the maximum room depth over which fresh air distribution would be effective. Further analysis was performed through numerical modeling. Gan [35] used CFD techniques to predict the air movement and local mean age of air in single-sided naturally ventilated rooms. The predicted airflow pattern, air temperature distribution, and local mean age of air distribution were used to determine the effective depth of fresh air distribution in the rooms. Air velocity and temperature were the parameters used as indicators for thermal comfort, while the local mean age of air was used as an index for indoor air quality. This method was applied to a room with single-sided ventilation through a single opening in summer. A sample set of results for the parameters of air velocity, air temperature, and normalized local mean age of air (with respect to the nominal time constant) is shown in Figure A 1. As discussed earlier, air velocity, air temperature, and local mean age of air dictated the maximum depth of the space by determining (a) the depth at which the fresh air velocity reached the room air velocity, (b) the interface location of fresh air and room air temperature, and (c) the location of the nominal time constant, respectively. For summer cooling, the requirement for thermal comfort (dictated by air velocity and air temperature distributions) was the limiting factor in determining the effective room depth, producing an effective depth of fresh air of between 7 m and 7.5 m, derived from Figure A la and b, respectively. The effective depth was found to be affected by the window size, room heat gains, and the outdoor temperature. 109 Velocity scale 0 1 2 3 4 1 m/s 5 - 6 - 9 9 10 11 12 13 14 15 3,UU E 1.M T-7- 7 0 - 0 1 2 3 4 8 5 7 8 9 10 11 12 13 14 is 10 11 12 13 14 15 11 12 IT, 11 12 13 14 15 (a) Air velocity (m/s) 0 1 31 2 "17 3 5 4 2 6 - ---- 1 2 8 8 9 S:- ~h~-r~i~% 1 0 7 4 5 ) 7mpr8A (I*6 (b) Air temperature (CC) 0 0 0 CC 1 2 3 2 5 4 6 7 8 9 10 4 AA A Room length (m) (c) Normallsed local mean age of air Figure A 1: Sample results from effective depth of fresh air study for a space with a 1 m wide window opening and a heat generation of 5 W/m 2 : (a) air velocity, (b) air temperature, and (c) normalized local mean age of air (with respect to the nominal time constant) [35] A.5 Convection and Radiation Component Calculation The following heat transfer equations were solved in order to derive the radiative and convective component of each of the indoor heat sources in this study (person, computer, television). 4 1s 2 Qrad Q = h(T, Q total = Qrad s(Ts- Tin 4 )A -Tin)A + (A-20, A-21, A-22) Q cony where Qrad = radiation heat transfer Qc = convection heat transfer El = emissivity of object = 0.9 62= emissivity of surroundings = 0.9 a = Stephan Boltzmann constant = 5.669 x 10-8 W/m 2K 4 110 T = surface temperature of heat source (parameter that is solve for) T = environmental air temperature = 28oC = 1.25 m2 A A= surface area of heat source (A person 1.61 M2 , A = 1.25 M 2 ) Equations A-20, A-21, and A-22 above were solved simultaneously for the three unknown parameters, These results Qrad' Qcony, and TS, for each of the three heat sources, and the results are shown in Table A 1. show that the radiative and convective heat components of each heat source are approximately 50%. Table A 1: Radiative and Convective Components for Heat Sources Heat Source Total Heat (W) Radiative Convective Heat (W) Radiative Convective (%) 52 Person 100 48.1 51.9 (%) 48 Television 300 158.5 141.5 53 47 Computer 300 158.5 141.5 53 47 (W) References - Appendix A Al. R.W. Hyland and A. Wexler. "Formulations for the thermodynamic properties of the saturated phases of H20 from 173.15 K to 473.15 K." ASHRAE Transactions 89 (2A) 1983: 500-19. A2. ISO. 1990. "Moderate thermal environments - Determination of the PMV and PPD indices and specification of the conditions for thermal comfort." Geneva, International ISO Standard 7730. A3. P.O. Fanger. "Thermal comfort analysis and applications in environmental engineering." New York: McGraw-Hill, 1970. A4.M.K. White and R.R. Walker. "The efficiency of single-sided and cross ventilation in offices spaces." Proc. 17th AIVC Conference - Optimum Ventilation and Air Flow Control in Buildings2, 17-20 September, 1996, Gothenburg, Sweden, 487-96. 111 APPENDIX B: CFD VALIDATION OF DISPLACEMENT VENTILATION CASE - CUBICLE OFFICE B. 1 Cubicle Office Case - CFD Model and Results After performing a validation on a factory type case, additional case was set up to simulate one of the experimental office type cases. The case chosen for simulation was the cubicle office case. The heat loads simulated in this case were 4 persons and 4 personal computers (see Table B 1). The experimental layout and CFD setup of this case are shown Figure B land Figure B 2, respectively. In the experiment, a single tracer-gas source was introduced from the top of the person simulator labeled Pl. The ten measuring locations designated in Figure B 1 are: Si, S2, S3, S4, S5, N1, N2, N3, N4, and N5. Table B 1: Heat Sources for Cubicle Office Case [381 Load ID PT P2 P3 P4 C1 C2 C3 C4 -- Description Person Simulator (Northwest) Person Simulator (Northeast) Person Simulator (Southeast) Person Simulator (Southwest) PC Simulator (Northwest) PC Simulator (Northeast) PC Simulator (Southeast) PC Simulator (Southwest) Lighting 112 Load (W) 75 75 75 75 92 92 88 88 732 Surface T ('C) 30.3 30.0 30.5 30.8 32.5 33.8 33.0 33.4 -- N ( S59 S4 L *N1 P PC ' racer Jas. S3 s2- > __T~_ I I 2PC PS PC ......... ......... PS *N3 a N4 0 N5 SI. TABLE (Front of Room) Figure B 1: Experimental layout of cubicle office case [38] N - I Figure B 2: CFD setup of cubicle office case 113 fi The CFD program was again validated by comparing the temperature (Figure B 3) and concentration (Figure B 4) values from the measured data with computed results. In Figure B 3, the agreement between the temperature measurements and computations is good. In Figure B 4, the concentration measurements and computations have some discrepancies, although the overall concentration patterns are similar. There are discrepancies apparent for the south measuring locations, where computational results greatly underestimat the concentration of SF 6 towards the upper part of the room. For the north measuring locations, the agreement and overall concentration patterns are better, although CFD both underpredicts and overpredicts the peaks in concentration at certain locations. This may be attributable to the slight mass imbalance in each of the experimental cases due to infiltration through the east sliding doors. 114 Z(m) Z(m) CO z I - cr) -~ -L NN 2(m) D m) zi w 2! --1 Z(m) 2(m) NI Co .5 2(m) 2(m) L- rl> LTD Po (M 2(m) - D (m) (M ) 1 NI C-) N) cn P1.) In , Figure B 3: Comparison of experimental and computed temperature profile for cubicle office case 115 Z(m) 0l )C) w. Z 4) (M) M~01 cr) CD, -2 _ (M TO *Z M) - (A q> 2(m) 0 z N) -0) 3 C N Z(m) m) J7NJJ __ _ i -.> I _ ; <r .1Cz / 3 2 m) 2(m) (M+ o4__~~ 3> *\Jz1 i / - 3 ____ 4 I~T*=**w f____ ____ ( m) Z (M) ND N ____ I M . C r 01 CO, 3 .............. ..................... ..................... .................... .............. ..... ................ Figure B 4: Comparison of experimental and computed SF 6 concentration for cubicle office case 116