* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Foundations of statistics wikipedia , lookup
History of statistics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Taylor's law wikipedia , lookup
Regression toward the mean wikipedia , lookup
Categorical variable wikipedia , lookup
Resampling (statistics) wikipedia , lookup
Basic Course in Statistics
for Medical Doctors
National Institute of Epidemiology
Chennai
nie
RESEARCH METHODOLOGY
nie
RESEARCH METHODOLOGY
Research: Careful study or investigation, specially
to discover new facts or information
Methodology : A set of methods used in a
particular area of activity
nie
TYPES OF RESEARCH
Basic Research - Fundamental for advances
- Not application-oriented
- Results totally unpredictable
- Requires major commitment
- Rapid results unlikely
Applied Research - Links advances with application
- Results are predictable
- Requires scientific training
- Rapid results likely
nie
STUDY DESIGNS IN
APPLIED MEDICAL RESEARCH
Approach
Type of study
1. Descriptive
Examples
- Institutional surveys
- Community surveys
Observational
2. Analytic
- Case-Control studies
- Cohort studies
- Lab experiments
Experimental
Analytic
- Animal experiments
- Clinical trials
nie
BASIC FRAMEWORK OF RESEARCH
• Problem : Identification, Need, Background
• Objective : Formulation, Hypothesis
• Method : Approach, Materials, Work Plan
• Population : Define Target Population & Study Population
• Measurements : Variables, Accuracy, Equipments
• Analysis : Data processing, Analysis, Inference
nie
INSTITUTIONAL SURVEY - EXAMPLE
• Problem :
HIV / AIDS - Prevalence - Control spread
- No vaccine - No cure - Propagate prevention
• Objective: To estimate awareness among youth
• Method:
Observational, Descriptive - College students- Survey
• Population: Youth - Chennai - College students - Sample
• Measurements: Knowledge - Self-administered questionnaire
• Analysis: Scrutinize - Code - Analyse - Estimate awareness
- Draw conclusions - Make inferences –
- Suggest messages
nie
COMMUNITY SURVEY - EXAMPLE
• Problem : Clinical anemia - Women & Children
- Foetal waste - Lowered IQ
• Objective : To estimate - Prevalence - Slum population
• Method : Observational, Descriptive - Slum dwellers - Survey
• Population : Slum dwellers - Chennai - Sample
• Measurements : Ht.(0.5 cm), Wt.(0.1kg),
Nutritional assessment
• Analysis : Scrutinize - Code - Analyse - Calculate prevalence
- Draw conclusions
nie
CASE - CONTROL STUDY
Exposure to risk factor
Yes
Select
cases
No
Yes
No
Select
suitable
controls
nie
CASE-CONTROL STUDY - EXAMPLE
• Problem :
Leprosy - Deformity development
- Dapsone regularity - Association
• Objective : To study the drug regularity and deformity
• Method :
Observational, Analytic - Deformed &
Un-deformed cases
• Population : Leprosy patients, LCU of TN, Matched controls
• Measurements : Deformity status, Drug regularity
• Analysis : Scrutinize - Code - Analyse - Calculate Odds Ratio
–Study association - Draw conclusions
nie
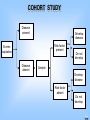
COHORT STUDY
Disease
present
Develop
disease
Time
Risk factor
present / /
Screen
population
Disease
absent
Do not
develop
Sample
Develop
disease
Time
Risk factor
/ /
absent
Do not
develop
nie
COHORT STUDY - EXAMPLE
• Problem :
Lung cancer - Smoking - Establish association
• Objective : To find out the association between smoking
& cancer
• Method :
Observational, Analytic - Adult - Men - Cohort Follow-up (FU)
• Population : Adult men - Cancer absent - Chennai - Sample
(Smokers & Non-smokers)
• Measurements : Smoking (No. / day), Clinical assessment,
X-ray , Biopsy
• Analysis : Scrutinize - Code - Analyse - Calculate Relative Risk
- Establish cause and effect - Draw inference nie
CASE-CONTROL Vs COHORT STUDY
CASE-CONTROL
MERITS
DEMERITS
COHORT
Takes Less time
Practically no bias
Non – expensive
Cause-effect can
be proved
Rare diseases can be
studied
Recall bias
Results
generalisable
Takes more time
Cause-effect can’t be
proved
Expensive
Results not
generalisable
Needs large
sample
Selecting suitable
control
Losses to follow-up
nie
nie
TABULATION
nie
TABULATION
• Condense and Present data
• Impress communication
• Data - A set of observations
Qualitative ( Sex, Religion)
• Data types
Quantitative
Continuous
(measurable)
Discrete
(countable)
Age
Hb
No. of. Children
No. of Cases
nie
SAMPLE DATA SET
Pt. No. Hb.
1
12.0
2
11.9
3
11.5
4
14.2
5
12.3
6
13.0
7
10.5
8
12.8
9
13.5
10
11.2
Pt. No.
11
12
13
14
15
16
17
18
19
20
Hb.
11.2
13.6
10.8
12.3
12.3
15.7
12.6
9.1
12.9
14.6
Pt. No.
21
22
23
24
25
26
27
28
29
30
Hb.
14.9
12.2
12.2
11.4
10.7
12.7
11.8
15.1
13.4
13.1
nie
TABULATION PROCEDURE
1. Find Min. & Max.
(9.1 & 15.7)
2. Calculate difference
(Max. – Min.)
(15.7 – 9.1 = 6.6)
3. Decide No. & width of classes (7, 1 g/dl)
4. Prepare a dummy table
(Hb, Tally, Frequency)
5. Tabulate (using tally marks)
nie
TABLE FREQUENCY DISTRIBUTION OF
30 ADULT MALE PATIENTS BY Hb
Hb (g/dl)
No. of patients
9.0 – 9.9
10.0 – 10.9
11.0 – 11.9
12.0 – 12.9
13.0 – 13.9
14.0 – 14.9
15.0 – 15.9
1
3
6
10
5
3
2
Total
30
nie
DIMENSION OF A TABLE
Dimension
= No. of variables according to which
the data are classified
One-way Table
- Freq. distn. of 30 adult male pts. by Hb
Two-way Table
- Freq. distn. of 30 adult pts. by Hb & Sex
Three-way Table - Freq. distn. of 30 pts. by Hb, Sex & Age
nie
ELEMENTS OF A TABLE
1. Number (To refer )
2. Title
(What, How classified, Where & When)
3. Column headings (concise & clear)
4. Foot-note (Headings, Special cell, Source)
nie
A TYPICAL EXAMPLE OF A ONE-WAY TABLE
Table II
Distribution of 120 (Madras) Corporation Divisions according to
annual death rate based on registered deaths in 1975 &1976
Death rate
(per 1000 p.a.)
6.0 – 7.9
8.0 – 8.9
9.0 – 9.9
10.0 – 10.9
11.0 – 11.9
12.0 – 12.9
13.0 – 13.9
14.0 – 14.9
15.0 – 15.9
16.0 –16.9
17.0 –18.9
19.0+
Total
No. of Divisions
4 (3.3)
13 (10.8)
20 (16.7)
27 (22.5)
18 (15.0)
11 (9.2)
11 (9.2)
6 (5.0)
2 (1.7)
4 (3.3)
3 (2.5)
1 (0.8)
120 (100.0)
Figures in parentheses indicate percentages
SOURCE:
Radhakrishna, S. et al (1983). Study of variation in area mortality rates in Madras city
& its correlates. IJMR, 78, 732 – 739.
nie
nie
GUIDELINES TO PREPARE A TABLE
1. Decide No. of classes
(5 - 15)
2. Decide Width of classes
(Equal / Unequal)
3. Decide class limits
(Closed / Open )
Precise ( 9.0 - 9.9 / 9 -10 )
Non-overlapping ( 9.0 - 9.9, 10.0 - 10.9, …/
9 - 10, 10 - 11…)
4. Use dummy tables & tally marks
5. Extract the table
nie
TABULATION - SUMMARY
• Data
• Qualitative
• Quantitative (Discrete, Continuous)
• Class – Number, Width , Limits
• Dummy table
• Tally marks
• Title
• Headings
• Foot-note (s)
nie
nie
AVERAGES
nie
THE ARITHMETIC MEAN (AM)
The AM of a set of values is the sum of all the values
divided by the number of values
The mean of 5, 6, 8 & 9 is
5+6+8+9
4
=
28
= 7
4
In general,
AM i.e., x =
x1 + x2+ ……+ xn
n
From this relationship, we get
=
xi
n
n x = xi
i.e., Number of values Mean = Sum of values
nie
PROPERTY OF ARTHMETIC MEAN
The addition / subtraction of a constant value to each of the
observations increases / decreases the mean by the same
constant
Similarly, if each observation is multiplied / divided by a
Constant value the mean is multiplied / divided by
the same value
Mean of 5 ,
6
, 8 ,
9
Mean of 5+2,
6+2, 8+2, 9+2
= 9
( = 7+2)
Mean of 5x3,
6x3, 8x3,
= 21
( = 7x3)
9x3
= 7
nie
MEAN OF SEVERAL GROUPS COMBINED
Group
(i)
Size
( n i)
Mean
( x i)
Sum
(ni xi )
1
10
41
410
2
15
36
540
3
25
42
1250
Total
50
--
2200
Mean of all groups = 2200 / 50 = 44
Crude average = 42.3
nie
THE GEOMETRIC MEAN
Let us calculate the GM of
5, 10, 20, 25 & 40 g / ml
Logarithm of these values are
0.70, 1.00, 1.30, 1.40 & 1.60.
The AM of log values is
0.70 + 1.00 + 1.30 + 1.40 + 1.60
6.00
=
5
= 1.20
5
The GM = antilog (1.20) = 15.85 g / ml
nie
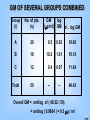
GM OF SEVERAL GROUPS COMBINED
Group
(i)
No. of pts.
(ni)
A
20
B
GM
(g/ml)
log
GM
ni . log GM
8.5
0.93
18.60
18
10.2
1.01
18.18
C
12
9.4
0.97
11.64
Total
50
--
--
48.42
Overall GM = antilog of ( 48.52 / 50)
= antilog ( 0.9684 ) = 9.3 g / ml
nie
EFFECT OF MULTIPLICATION / DIVISION
If each observation is multiplied / divided by a constant value,
the GM is multiplied / divided by the same value
EFFECT OF ADDITION / SUBTRACTION
The new GM will have to be calculated from the first principles
as there is no simple relationship with the old GM
LIMITATIONS OF GM
• Even if one value is negative the GM cannot be calculated
• If any value is zero the GM will also be zero
nie
THE MEDIAN
Suppose we wish to find the median of the following values
10, 20, 12, 3, 18, 16, 14, 25, 2
Arranging the numbers in increasing order, we have
2 , 3, 10, 12, 14, 16, 18, 20, 25; Median = 14
Suppose one more observation, say 8 , is included.
Then, we have
2 , 3, 8, 10, 12, 14, 16, 18, 20, 25
Median
= Mean of 12 & 14 = 13
nie
ANOTHER EXAMPLE FOR MEDIAN
Duration (days) of absence from work of 21 labourers owing
to sickness
1, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 6, 6, 6, 7, 8, 9, 10, 10, 59, 80
AM = 11 days
Not typical of the series as 19 of the 21 labourers were absent
for less than 11 days
The Median of 5 days would be a better measure
nie
DISADVANTAGES OF MEDIAN
• If two groups of observations are pooled, the median of the
pooled group cannot be estimated from the individual group
medians
• Median is less efficient than mean, as it takes no account of
the precise magnitude of most of the observations
• The median is much less amenable than the mean to
mathematical treatment, and is not much used in the more
elaborate statistical techniques
nie
THE MODE
• The value that occurs most frequently
• It is not widely used in analytical statistics
• It can be obtained when some characteristic itself cannot be
measured (colour that people prefer for their cars)
Colour preference
Green
Blue
Grey
Red
No. of persons
354
852
310
474
Mode = Blue
nie
THE HARMONIC MEAN (HM)
One drives equal distances at a speed of 20, 25 & 30 mph
The average speed is not 25 mph i.e., the A.M.
A drive of 300 miles
At 20 m.p.h. - 15 hours 900 miles in 15 + 12+10 = 37 hrs
25 ,,
- 12 ,,
30 ,,
- 10 ,,
Average = 900 / 37 = 24.3 mph
Formula for HM
Speed (x) 1/x
20
0.05
25
0.04
30
0.0333
-----------------------Total
0.1233
Ave. of reciprocals
= 0.1233 / 3 = 0.0411
Reciprocal of Ave. of reciprocals
= 1 / 0.0411 = 24.3 mph
nie
SELECTION OF THE APPROPRIATE MEASURE
The choice depends upon the nature of the data
• If the data are symmetrically distributed, any one of these
measures can be used
• For skewed distributions, the AM is not suitable
( + vely skewed: AM gives a higher value
– vely skewed: AM gives a lower value)
• If some observations deviate much more than others in the
series, then median is appropriate
• The AM has definite advantages if subsequent computations
are needed
nie
FREQUENCY TABLE
Weight (kg)
No. of pts.
20.0 – 24.9
25.0 – 29.9
30.0 – 34.9
35.0 – 39.9
40.0 – 44.9
45.0 – 49.9
50.0 – 54.9
2
4
20
33
33
5
3
Total
100
1. Width of class interval should be same
2. It is advisable to have not more than 20 classes
3.The limits of the intervals must be unambiguously stated
nie
FREQUENCY TABLE
Calculation of Mean
Dose of drug No. of pts. Mid point of
received
class interval
(fi)
(xi)
fi xi
0 - 4
1
2
2
5 - 9
5
7
35
10 - 14
7
12
84
15 - 19
24
17
408
20 - 24
56
22
1232
25 - 29
30
27
810
Total
Mean
123
---
2571
= 2571 / 123 = 20.9 21 doses
nie
FREQUENCY TABLE
Calculation of Median
Weight
(kg)
20.0
25.0
30.0
35.0
40.0
45.0
50.0
Median
-
24.9
29.9
34.9
39.9
44,9
49.9
54.9
No. of pts.
(fi)
Cumulative
frequency
2
4
20
33
33
5
3
2
6
26
59
92
97
100
= Middle value =
=
=
=
50th value
34.95 + {5 / 33 (50-26)}
34.95 + {5 / 33 24}
38.59 kg
nie
DIAGRAMS
nie
DIAGRAMS
Why diagrams?
• Difficult to understand raw data
• Tables & Diagrams help in understanding
• Tabulation - overall picture
• Diagrams - Pattern & Shape
- Meaningful impression in mind
- Get across a point quickly
- Sacrifice details & accuracy of data
nie
TYPES OF DIAGRAMS
Type of Variable
Qualitative or discrete
(religion, gender,
Diagram
Bar diagram
Pie chart
place of residence)
Continuous
(height, weight, blood sugar )
Histograms
Line diagrams
nie
BAR DIAGRAM
• Used when data are qualitative or discrete
• Height of a bar is proportional to the frequency
• Width of each bar is same.
• Multiple bars can be drawn in the same diagram.
nie
Table 1 Risk factors for Myocardial Infarction for patients (n=57)
admitted to the Kilpauk Medical College Hospital,
Chennai, Jan- Sep 1998
Risk factor
MI Patients
No
%
Hypertension
24
42.1
Smoking
20
35.1
Diabetes
13
22.8
CAD
9
15.8
Hyperlipedemia
2
3.5
None
8
14.0
nie
Fig. 1 Risk factors for Myocardial Infarction for patients (n=57)
admitted to the Kilpauk Medical College Hospital,
Chennai, Jan- Sep 1998
45
42.1
40
35.1
35
30
22.8
25
20
15.8
14
15
10
3.5
5
0
Hypertension
Smoking
Diabetes
CAD
Hyperlipedemia
None
nie
PIE DIAGRAM
• Considered for qualitative or discrete data
• A circle is divided into different sectors
• Areas of sectors are proportional to frequencies
nie
Table - 2 Distribution of newly detected leprosy patients
by Type, Govt. Leprosy Treatment & Study Centre,
Arakandanallur, 1955-57
Type
L
Patients
No.
%
689
17.9
Angle
(Degrees)
64
N?L
157
4.1
15
N
2999
78.0
281
Total
3845
100.0
360
nie
Fig 2 Distribution of newly detected leprosy patients
by Type, Govt. Leprosy Treatment & Study Centre,
Arakandanallur, 1955-57
N?L
4%
L
18%
N
78%
nie
HISTOGRAM
• Essentially a bar diagram
• Bars are drawn continuously
• Width - usually equal
• Area - proportional to frequencies
nie
Table 3 Frequency distribution of Haemoglobin levels
of adult male patients (n=30)
Hb (g/dl)
9.0
- 9.9
10.0 - 10.9
11.0 - 11.9
12.0 - 12.9
13.0 - 13.9
14.0 - 14.9
15.0 - 15.9
Total
No. of patients
1
3
6
10
5
3
2
30
nie
Fig. 3 Frequency distribution of Haemoglobin levels
of adult male patients (n=30)
12
No. of patients
10
8
6
4
2
0
9.0 - 9.9
10.0 - 10.9
11.0 - 11.9
12.0 - 12.9
13.0 - 13.9
14.0 - 14.9
15.0 - 15.9
Hb level (g/dl)
nie
LINE DIAGRAM
• Diagram is drawn by taking
X – axis - time (e.g., Years)
Y – axis - value of any index or quantity
(e.g., couple protection rate)
• Displays how a variable has changed over time
nie
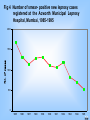
Table 4 Number of smear- positive new leprosy cases
registered at the Acworth Municipal Leprosy
Hospital, Mumbai, 1985-1995
Year
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
No. of cases
Registered
1681
1319
1143
1287
1317
1103
1060
1176
825
706
528
Source: Juwatkar PS, Chulawala RC, Naik SS.Correspondence
Indian J Lepr 1997;62 (2):197
nie
Fig 4 Number of smear- positive new leprosy cases
registered at the Acworth Municipal Leprosy
Hospital, Mumbai, 1985-1995
2000
1500
1000
500
0
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
nie
nie
VARIATION
nie
VARIATION
• Measurement of variation is very important
- Mean blood pressure of a group of subjects is 110 mm Hg
- Mean value alone is not sufficient
- One is also interested in knowing how much the blood pressure
varies from one subject to the other
- Reliability of the mean of 100 values depends upon the extent to
which the 100 values differ
• Smaller the variation the greater will be the reliability
• Extreme case of no. variation, the mean is determined with
certainty and is equal to common value
• Measurement of variation also plays an important role in the
methods of statistical significance
nie
IMPORTANCE OF MEASURING VARIABILITY
Marks obtained
Students
Biology
Physics
Chemistry
1
200
199
100
2
200
200
200
3
200
201
300
Mean
200
200
200
Variation
NIL
VERY SLIGHT
SUBSTANTIAL
Range
0
2
200
nie
LIMITATIONS OF RANGE
• Range depends only on 2 of the many values measured, i.e., highest & lowest
• It gives no information whatsoever about the other values; These could be
spread evenly, unevenly, or clumped around a particular value
For e.g.,
x-----x-----x----x----x----x----x----x----x----x----x
30
40
50
60
65
Evenly
x------x-----------xxxx---x-----------xx------x-----x
30
40
50
60
65
Unevenly
x-------------------------xxxxxxxxxx--------I------x
30
40
50
60
65
Clumped
35 Kg
35 Kg
35 Kg
nie
LIMITATIONS OF RANGE
• Range increases with sample size
Initial set
(5 values)
30, 40, 53, 58, 65
Range
30 – 65
35
New set
(3 values)
48, 51, 64
30 – 65
35
New set
(3 values)
48, 51, 70
30 – 70
40
New set
(3 values)
28, 51, 70
28 – 70
42
• Two ranges based on different sample sizes are not comparable
nie
LIMITATIONS OF RANGE
Range can be distorted by aberrant values, which may be
genuine or may be due to experimental errors
ESR (mm) at 1 hour
Range
4, 8, 11, 14, 20
4 -- 20
16 mm
4, 8, 11, 14, 120
4 -- 120
116 mm
nie
INTER-QUARTILE DISTANCE
Median breaks the distribution into 2 equal parts
Q1 divides the distribution in the ratio of ¼ : ¾
Q3 divides the distribution in the ratio of ¾ : ¼
Inter-Quartile distance = Q3 – Q1
Useful when the number of observations is large
nie
STANDARD DEVIATION
“Average measure of variation of each observation from the mean ”
Arithmetic mean = 45 / 5 = 9 x-rays
Absolute or Mean deviation = 8 / 5 = 1.6 x-rays
Variance = [20 / (5 –1)] = 20 / 4 = 5 x-rays
{[425 – ((45)2/5)] / 5-1 = 20}
nie
STANDARD DEVIATION- ALTERNATIVE DEFINITION
10, 8, 6, 12, 9
Mean = 9
Sum of squares of differences between pairs of observations
12
2 4
10
1 1
9
1 1
8
2
6
4
3
1
9
1
0
0
-1
-3
1
9
20
4
3 9
2 4
3 9
10
4 16
4 16
21
6 36
65
65 + 21 + 10 + 4 = 100
Sum of squares of differences
between Pairs of observations
No. of observations = 100/5 = 20
Sum of squares of deviations from mean
= 20
nie
PROPERTIES OF STANDARD DEVIATION
Unaffected if same constant is added to
(or subtracted from) every observation
If each value is multiplied ( or divided ) by a
constant, S.D. also is multiplied (or divided)
by the same constant
nie
COEFFICIENT OF VARIATION
Standard deviation is expressed in the same unit as the mean
- e.g., 3 cm for height, 1.4 kg for weight
Sometimes, it is useful to express variability as a percentage of the mean
- e.g., in the case of laboratory tests, the experimental variation is 5% of the mean
Coefficient of variation (%) = [S.D / Mean] x 100 (Pure number)
The coefficient of variation can be used to compare:
1. the variability in two variables studied which are measured in different units
- height (cm) and weight (kg)
2. the variability in two groups with widely different mean values
- incomes of persons in different socio- economic groups
nie
WHICH MEASURE OF DISPERSION?
Measure
Range
Advantages
Disadvantages
1. Most obvious
1. Uses only 2 observations
2. Very easy to calculate
2. It increases with the
size of sample
3. Can be distorted by
aberrant values
Inter – Quartile distance
Not affected by extreme values 1. Uses only 2 observations
2. Not amenable for further
statistical treatment
Standard deviation
1. Uses every value of the data
Highly influenced by
2. Suitable for further analysis
extreme values
nie
CALCULATION OF S.D. FROM
FREQUENCY DISTRIBUTION BY SHORT-CUT METHOD
Age
(years )
25 - 34
35 - 44
45 - 54
55 - 64
Mid-point Working unit
(y)
30
0
40
1
50
2
60
3
Total
No. of Pts.
(f)
15
25
8
2
50
fy
0
25
16
6
47
fy2
0
25
32
18
75
Working unit y = (Age - 30) / 10
Sum of squares of deviations from mean = 75 - (47)2/50 = 30.82
Variance = 30.82 / 49 = 0.629
S.D.
= 0.629
= 0.793
S.D. in original units = 0.793 x 10 = 7.93
nie
nie
PROBABILITY
nie
CONCEPT OF PROBABILITY
Suppose
1) Success rate of a program to stop smoking is 75% compared to
the expected 70%
2) The mean height of 200 adults in a suburban area of a
city is 165 cm compared to the city’s mean height of 170 cm
3) In a trial involving 100 pts. treatment A is better than
treatment B
Can we really be certain that
1) Program is successful?
2) Height is less in suburbs ?
3) Treatment A is better than treatment B?
Questions like these cannot be answered with a simple ‘Yes’ or ‘No’
nie
DEFINITION OF PROBABILITY
•
The use of experience as a relative frequency
Suppose a coin is tossed 10,000 times and head(H) has occurred
4,980 times, then the relative frequency of
H = 4,980 10,000 = 0.498 0.5
•
The theoretical approach
Assuming that the coin is fair, which means that
both head (H) & tail (T) have equal chance of occurring
i.e., No. of outcomes of interest (say, Head)
=1/2
No. of possible outcomes
i.e P(H) = 1/2 & P(T) = 1/2
nie
DEFINITION OF PROBABILITY
We shall define probability as a Proportionate frequency
If a variable can take any of N values and n of these
constitute the event of interest to us, the probability of the
event is given by n / N
i.e. No. of outcomes of interest
Total no. of outcomes
nie
TOSSING A COIN
There are 2 possible outcomes
- HEAD or TAIL
In a toss,
Prob. of getting a Head
=1/2
Prob. of getting a Tail
=1/2
nie
THROWING A DIE
There are 6 possible outcomes
-- 1, 2, 3, 4, 5 or 6.
In a throw,
Prob. of getting a score of 1 = 1/6
Prob . of getting a score of 4 = 1/6
nie
DRAWING A CARD FROM A PACK
There are 52 cards in a pack of playing cards which
includes:
4 Aces, 2 Red & 2 Black
A card is randomly picked from the pack
Prob. of getting an Ace
= 4/52
Prob. of getting a Black Ace
= 2/52
Prob. of getting a Red Ace
= 2/52
nie
SELECTION OF A SUBJECT
In a small community, there are 800 subjects
Of them, 128 are aged under 5 yr, 192 aged 5–15 yr and 480
aged above 15 yr
A subject is selected at random
Prob. of selecting a child under 5 yr
= 128 / 800 = 0.16
Prob. of selecting a child between 5 & 15 yr = 192 / 800 = 0.24
Prob. of selecting a child under 15 yr
= 128+192 / 800
= 320 / 800 = 0.40
nie
RULE OF MULTIPLICATION
Independent events
P(A) = Probability of an event A occurring
P(B) = Probability of an event B occurring
The two events A and B are said to be independent if
the occurrence of one has no implications on the other
In this case, the probability of both A and B occurring at
the same time is the product of the two individual
probabilities
P(AB) = P(A) X P(B)
nie
ILLUSTRATION
Event A - Obtaining HEAD on tossing a coin
Event B - Obtaining a ‘score of 6’ on throwing a die
P(A) = 1/2
;
P(B) = 1/6
A coin is tossed & a die is thrown simultaneously
The outcome of the toss of the coin has no implication on the
result of the throw of the die
These two events are independent
Probability of getting ‘HEAD’ and a ‘score of 6’, when a coin
is tossed and a die is thrown simultaneously, is given by
1/2 x 1/6 = 1/12
nie
CHECKING FROM FIRST PRINCIPLES
Outcomes
Tossing a coin
Throw of a die
- Head or Tail
- 1, 2, 3, 4, 5, or 6
Possible outcomes
(H,1) ; (H,2) ; (H,3) ; (H,4) ; (H,5) ; (H,6);
(T,1) ; (T,2) ; (T,3) ; (T,4) ; (T,5) & (T,6)
Total possible outcomes = 12
Outcome of interest = Head & a score of 6 = 1
Required Prob. = 1 / 12
nie
Non - Independent events
If the events A and B are not independent, then
P(AB) = P(A) x P(B, given A)
= P(B) x P(A, given B)
nie
ILLUSTRATION
Consider a group of 5 persons - 3 Males & 2 Females
M1, M2, M3, F1, F2
Suppose one person is selected at random, and then a second
one is selected, again at random, from the remaining 4 persons
Prob. of selecting a Male on both the occasions :
I Occasion :
Prob. of selecting a male = 3 / 5 (M2)
II Occasion :
There are 4 persons left (M1, M3, F1, F2)
Prob. of selecting a male = 2 / 4
Prob. of selecting a male on both occasions
= 3 / 5 x 2 / 4 = 6 / 20
nie
CHECKING FROM FIRST PRINCIPLES
The first person can be selected in 5 ways
M1 or M2 or M3 or F1 or F2
Associated with each of these the second person can be
selected in 4 ways (e.g. M1 or M3 or F1 or F2 following M2)
Total No. of ways in which 2 persons can be selected
= 5 x 4 = 20
Selection of a Male
I occasion - 3 ways
II occasion - 2 ways
Total no. of ways in which 2 males can be selected
=3x2=6
Required Prob. = 6 / 20
nie
RULE OF ADDITION
Mutually exclusive events
P(A) = Probability of an event A occurring
P(B) = Probability of an event B occurring
The two events A and B are said to be mutually exclusive if
they cannot occur together
In this case, the probability that one or the other occurs is
simply the sum of the two individual probabilities
P(A or B) = P(A) + P(B)
nie
EXAMPLE
Consider a single throw of a die
Prob. of getting a score of 3 = 1/6
Prob. of getting a score of 5 = 1/6
3 and 5 cannot occur at the same throw
Prob. of getting 3 or 5
= 1/6 + 1/6
= 2/6
nie
EVENTS THAT ARE NOT MUTUALLY EXCLUSIVE
Events A and B do occur together on some occasions
In such situations, there is a need to modify the formula
The modified formula reads as
P(A or B or both) = P(A) + P(B) - P(AB)
nie
EXAMPLE
In a clinical trial,
Proportion of male patients
Proportion of young patients
= 0.60
= 0.80
We wish to determine the prob. of pts. who were either male or young or both
0.6 + 0.8 = 1.4, absurd result
(Male and Young are counted twice)
Sex and Age are independent
Young
Male
0.48
Female 0.32
Total
0.80
Old
0.12
0.08
0.20
Total
0.60
0.40
1.00
Prob. of male & young = 0.6 x 0.8 = 0.48
Proportion who are either male or young
( or both) = 0.6 + 0.8 - 0.48 = 0.92
nie
LABORATORY EXAMPLE
No. of
contaminated
cultures
0
1
2
3
Total
No. of Proportionate
patients
frequency
364
122
13
1
500
0.728
0.244
0.026
0.002
1.000
Prob. of ‘0’ contaminated culture = 0.728
Prob. of getting at least 2 contaminated cultures
= Prob. of getting 2 cont. cultures + Prob. of getting 3 cont. cultures
= 0.026 + 0.002 = 0.028
nie
nie
NORMAL DISTRIBUTION
nie
NORMAL DISTRIBUTION
nie
NORMAL DISTRIBUTION
Parameters : Mean and Standard deviation (S.D)
nie
STANDARD NORMAL DISTRIBUTION
The mean specifies the location and the s.d. specifies the
spread of the distribution
Hence, for different values of mean or s.d. or both, we get
different Normal distributions
However, every Normal distribution can be standardized
in terms of a quantity called the Normal deviate, which is
defined as
Observation - Mean
Z = ------------------------------Standard deviation
The probabilities associated with Normal distribution are
obtained from the knowledge of Z
nie
USE OF NORMAL DISTRIBUTION
Example 1:
Mean height
= X = 65"
Standard deviation = SD = 2"
a) Proportion of persons whose height
exceeds 68"
Normal deviate = Z =
X- X
SD
Area Under Curve (AUC) Normal
from Z = 1.5 to
=
68-65
2
= 1.5
} = 6.68%
= 0.06681
(height exceeds 68")
nie
b) Proportion of persons whose height is less than
60"
X- X
Normal deviate = Z= SD
= (60 - 65 ) / 2
= - 2.5
AUC Normal
from Z = - to -2.5
}
=
AUC Normal
from Z = 2.5 to
(height less than 60") = 0.00621
= 0.6 %
nie
c) Proportion of persons whose height is in between 64 " & 67 "
64 - 65
Normal deviate ( X=64") = Z1 = ----------- = - 0.5
2
AUC Normal
AUC Normal
from Z1 = - to - 0.5 = from Z1 = 0.5 to
(height less than 64”) = 0.30854
}
67 - 65
Normal deviate ( X=67") = Z2 = ----------- = 1
2
AUC Normal
from Z2 = 1 to = 0.15866
(height more than 67")
AUC Normal
(heights between 64" & 67’’)
= 1 - 0.30854 - 0.15866 = 0.5328 = 53.28%
nie
Example 2:
Mean cholesterol = 242 mg% ; S.D. = 45 mg%
a) What is the cholesterol level exceeded by 10% of the men?
We have to find the Z corresponding to an area of 10% (0.1)
on the right. The approximate Z value from the table is 1.3
X -X
------- = Z
SD
X - 242
------------ = 1.3
45
X - 242 = 1.3 x 45 = 58.5
X = 58.5 + 242 = 300.5 mg%
nie
b) What is the cholesterol level that exceeds the Cholesterol
level in 2.5% of the men ?
We have to find the Z corresponding to 2.5% of the area (0.025)
on the left. From the table the Z corresponding to an upper area
of 0.025 is 1.96. Hence, by symmetry, the lower value of Z is 1.96
X -X
------- = Z
SD
X - 242
---------- = -1.96
45
X – 242
X
= -1.96 x 45 = - 88.2
= 242 - 88.2 = 153.8 mg%
nie
nie
CONCEPT OF TEST OF SIGNIFICANCE
nie
• Research studies to test hypothesis
• Experiment & data collection
• Based on available data inference about
hypothesis
• Significant difference – subjective
• Statistical significance
nie
• Studies are on sample of subjects and not
on entire population
• Sampling variation
• Allowance should be given for sampling
variation while decision taking
nie
SAMPLING FLUCTUATION
Means of random
samples of 100
subjects
66”
Population
of 10,000
Mean height = 65”
S.d. = 10”
Sampling error of mean
=1
67”
63”
65”
64”
• Even when statistically sound sampling techniques are employed the
Mean in samples of 100 will not necessarily be 65”, but will vary from
sample to sample.
This is called sampling fluctuation
This must be taken into account when interpreting differences.
The method by which we do this is called a SIGNIFICANCE TEST
nie
Magnitude of allowance : 10% ?
5%?
Consider an expected difference of 0%
1%, 2%, 3% - not large
20%, 30% - very large, not willing to consider the diff. as 0%
WHY ?
If the true difference is 0%, chance (probability) of getting a
difference of 20% etc. is very small
nie
Formulate a decision rule based on the probability of
getting the observed difference
Null hypothesis (Ho)
Assuming Ho is true , compute the probability of obtaining
the Observed difference
If the probability is low reject Ho, else accept Ho
nie
Definition of low probability: Can be subjective
Conventionally, low probability = 5% (P=0.05)
If P < 0.05, the observed difference is
‘SIGNIFICANT (Statistically)’
P< 0.01, sometimes termed as ‘Highly Significant’
Computation of P-values, a statistical exercise
It depends on the nature of data and design of the study.
nie
CONCEPT OF TEST OF SIGNIFICANCE
Population of
10, 000
A random sample
of size 100 is drawn
Mean height = 68”
Question : Could the population mean be 65” ?
Hypothesis : Population mean = 65”
Question : What is the probability of obtaining a sample mean
of 68” from this population when sample size = 100 ?
If this probability is small (e.g. < 5%), Reject the Hypothesis.If
not, Accept the Hypothesis
nie
TEST OF SIGNIFICANCE
COMPUTATION OF PROBABILITY
Observed Mean
= 68”
Standard deviation = 10”
Postulated Mean = 65”
Sample size
= 100
Sampling error (s.e.) of mean = 10 / 100 = 1
Compute
Observed Mean - Postulated Mean
68-65
----------------------------------------- = -------- = 3
s.e. of mean
1
Critical value for significance at 5% level = 1.96
Since 3 > 1.96, we infer that the difference is Statistically
significant
Exact probability = 0.0027 , i.e., 0.27%
nie
WHAT IF DISTRIBUTION IS NOT “NORMAL”?
Transform the data (e.g. drug concentration, cell counts)
to some other scale - e.g. logarithm, square root,
to obtain a Normal distribution.
If not feasible, and provided sample size exceeds 30, make use
of the result that mean is approximately Normally distributed.
nie
Two types of errors
Type I : Rejecting Ho when it is true
Type II : Accepting Ho when it is false
Reducing one, will increase the other
Which is more important?
Depends on situation
Criminal proceedings
Specify Type I error and reduce Type II error to any given
level by adjusting sample size
Power of test : Prob. of rejecting Ho when it is false
Ho: True , False , Prove, Disprove.
nie
WHICH ERROR IS MORE IMPORTANT?
Tuberculosis
Effective drugs available?
MANY
Cancer
VERY FEW
Concluding that New treatment UNFORTUNATE
is better when it is not
NOT SO
UNFORTUNE
Concluding that New treatment NOT SO
is no better when it is better
UNFORTUNATE
VERY
UNFORTUNATE
Which error is more important?
TYPE II
TYPE I
nie
INTERPRETATION OF SIGNIFICANCE
SIGNIFICANT
Does not necessarily mean that the
observed difference is REAL or
IMPORTANT. Only that it is unlikely
(< 5%) to be due to chance.
Trivial differences can be statistically significant
if they are based on very large numbers.
nie
INTERPRETATION OF NON - SIGNIFICANCE
NON - SIGNIFICANT
Does not necessarily mean that
there is no real difference; it means
only that the observed difference
could easily be due to chance
(Probability of at least 5%)
There could be a REAL or IMPORTANT difference but due to
INADEQUATE sample size we might have obtained a
non-significant result
nie
• One - sided test
• Actual P - Values to be quoted
• Statistical significance and Clinical significance
nie
nie
TEST FOR PROPORTIONS
nie
• Data collected in the field of medicine is often qualitative
Classification of pregnancy (High-risk or Not high-risk)
Degree of severity of a disease (Mild, Moderate or Severe)
Outcome after treatment (Cured or Not cured)
• The measure computed in the above instance is a
‘PROPORTION’
• This corresponds to mean in the case of quantitative data
such as height, weight, cholesterol etc.
Comparison of proportions:
The test employed is called the “CHI – SQUARE TEST”
nie
THE CHI – SQUARE TEST
The Chi – square test examines whether a series of observed (O)
numbers in various categories are consistent with the numbers
expected (E) in those categories on some specific hypothesis
(Null hypothesis)
2
= 0 when every Observed = Expected
If the calculated value of 2 exceeds the tabulated value under
the column P = 0.05, the Null hypothesis is rejected
nie
COMPARISON OF A OBSERVED PROPORTION
WITH A HYPOTHESISED ONE
Hypothesis : A pharmaceutical company claimed that their
new product can cure 80% of the patients
Data :
56 out of 80 with disease got cured (i.e. 70%)
Cured
56 (64)
2
Not Cured
Total
24 (16)
80
(56 - 64)2
(24 - 16)2
= --------+ ---------64
16
(-8)2
(8)2
64
= ----- + ----- = ------ +
64
16
64
64
-----16
= 1+4 =5
• The calculated value of 2 (i.e., 5) with 1 degree of freedom exceeds the
table value (3.84) at 5% level
• Hence, we reject the Null hypothesis that the efficacy of the new product is 80%
nie
PERCENTAGE POINTS OF X2 DISTRIBUTION
Degrees of
Freedom
1
2
3
4
5
6
7
8
9
10
15
20
30
0.10
2.71
4.61
6.25
7.78
9.24
10.64
12.02
13.36
14.68
15.99
22.31
28.41
40.26
Probability of greater value
0.05
0.01
3.84
6.63
5.99
9.21
7.81
11.34
9.49
13.28
11.07
15.09
12.59
16.81
14.07
18.48
15.51
20.09
16.92
21.67
18.31
23.21
25.00
30.58
31.41
37.57
43.77
50.89
0.001
10.83
13.82
16.27
18.47
20.52
22.46
24.32
26.12
27.88
29.59
37.70
45.32
59.70
nie
COMPARISON OF PERCENTAGES
FROM 2 SAMPLES
Cure rate - Treatment A : 90% ; 90 out of 100
- Treatment B : 70% ; 105 out of 150
Treatment Cured
Not cured Total
A
90 (78)
B
105 (117)
45 (33)
150
195
55
250
Total
10 (22)
100
(90 - 78)2
(10 - 22)2 (105 - 117)2 (45 - 33)2
2 = ------------ + ------------ + --------------- + ----------- =
78
22
117
33
13.99
• The calculated value of 2 (i.e., 13.99 ) with 1 degree of freedom exceeds the
table value (3.84) at 5% level
• Hence, we reject the Null hypothesis that the two treatments are equally effective
nie
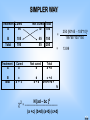
SIMPLER WAY
Treatment Cured
A
B
Total
Treatment
A
B
Total
90
105
195
Cured
a
c
a + c
Not cured Total
10
100
45
55
Not cured
b
d
b+d
=
250 {90*45 - 105*10}2
195*55*100*150
=
13.99
150
250
Total
a+b
c+d
a+b+c+d =
N
N [ad – bc ]
2
= --------------------------------------------------2
(a +c) (b+d) (a+b) (c+d)
nie
CORRECTED CHI – SQUARE
N [ |ad – bc| - N / 2 ]
2
Corrected = ----------------------------------------------------2
(a +c) (b+d) (a+b) (c+d)
Corrected 2 =
250 [ |90 x 45 – 105 x 10 | –125]2
= 12.84
195 x 55 x 100 x 150
Note that the corrected value will always be smaller than
the uncorrected which tends to exaggerate the
significance of a difference
nie
CHI – SQUARE TEST ON PAIRED OBSERVATIONS
100 pts. received two drugs A & B in a random sequence
15 manifest toxicity to A
5 to B (including 4 to both A & B)
Compare toxicity 15 / 100 Vs 5 / 100
- Incorrect, as the “same” as 100 patients are tested twice
nie
CHI – SQUARE TEST ON PAIRED OBSERVATION
100 patients received two drugs A & B in a random sequence
Group
Drug A
Drug B
Example
General case
(1)
Toxic
Toxic
4
a
(2)
Toxic
Not toxic
11
b
(3)
Not toxic
Toxic
1
c
(4)
Not toxic
Not toxic
84
d
Groups (1) & (4) make no contribution
Considering groups (2) & (3), the expected number of patients in
each, under the Null hypothesis that the 2 drugs have the same
toxicity, is (11+1) / 2 = 6
nie
Observed
11
1
Group (2)
Group (3)
2=
(11 – 6 )2
(1 – 6)2
----------- + ------------ =
6
6
This expression is same as
Expected
6
6
25 25
----- + ----- = 8.33
6
6
(11- 1)2 / (11 + 1) = 8.33
Applying correction for continuity
2=
(|11 – 1| - 1)2
-----------------------------
= 6.75
11+1
As the calculated value of X21 (6.75) exceeds the Table value (3.84)
at 5% level, we reject the Null hypothesis
In general ,
2=
[|b-c| - 1]2
-------------------
(b +c)
nie
EXAMPLE OF A 4 x 2 TABLE
Cataract
Religion
Present
Hindu
10 (9.7)
90
100
Muslim
4
46
50
Christian
3
22
25
Others
1
9
10
Total
18
167
185
Absent
Total
d.f. = (No.of rows – 1) x (No.of columns –1)
= (4-1) x (2-1)
=3x1
=3
nie
TREND CHI – SQUARE TEST
Extent of
Disease
Response to treatment
Favourable
Unfavourable
Total
Mild
44
6 (12%)
50
Moderate
85
15 (15%)
100
Severe
120
30 (20%)
150
Very severe
75
25 (25%)
100
Total
324
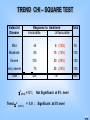
2(df=3) = 5.1 ;
Trend 2 (d.f.=1)
= 5.0 ;
76
400
Not Significant at 5% level
Significant at 5% level
nie
To sum up
• Chi- square test should be applied on qualitative data
set out in the form of frequencies.
• Chi – square test should not be done on
- Percentages / Rates / Ratios / Mean values
• Paired nature of the observations should be kept in mind
• Natural ordering in groups should be taken into account
nie
PRECAUTIONS
1. When sample size is small,other exact tests are to be
preferred
2. When several expected cell frequencies are less than
one, it is better to amalgamate rows / columns
nie
nie
SCATTER DIAGRAM
nie
SCATTER DIAGRAM
The simplest method to assess relationship between two
quantitative variables is to draw a scatter diagram
From this diagram we notice that as age increases there is a
general tendency for the BP to increase. But this does not
give us a quantitative estimate of the degree of the relationship
nie
CORRELATION COEFFICIENT
The correlation coefficient is an index of the degree of
association between two variables. It can also be used for
comparing the degree of association in different groups
For example, we may be interested in knowing whether the degree of
association between age and systolic BP is the same (or different) in
males and females
The correlation coefficient is denoted by the symbol ‘r’
‘r’ ranges from -1 to +1
nie
High values of one variable tend to occur with high
values of the other (and low with low)
In such situations, we say that there is a positive correlation
High values of one variable occur with low values of the other
(and vice-versa)
we say that there is a negative correlation
nie
A NOTE OF CAUTION
Correlation coefficient is purely a measure of degree of
association and does not provide any evidence of
a cause-effect relationship
It is valid only in the range of values studied
Extrapolation of the association may not always be valid
Eg.: Age & Grip strength
nie
r measures the degree of linear relationship
r = 0 does not necessarily mean that there is no
relationship between the two characteristics under
study; the relationship could be curvilinear
Spurious correlation :
The production of steel in UK and population in India
over the last 25 years may be highly correlated
nie
r does not give the rate of change in one variable
for changes in the other variable
Eg: Age & Systolic BP - Males : r = 0.7
Females : r = 0.5
From this one should not conclude that Systolic BP increases
at a higher rate among males than females
nie
PROPERTY OF
CORRELATION COEFFICIENT
Correlation coefficient is unaffected by addition / subtraction
of a constant or multiplication / division by a constant to all the
values of X and Y
Corr. Coeff. between X & Y
= 0.7
,,
X+10 & Y-6 = 0.7
,,
5X & 2Y
= 0.7
If the correlation coefficient between height in inches and
weight in pounds is say, 0.6, the correlation coefficient
between
height in cm and weight on kg will also be 0.6
nie
COMPUTATION OF THE
CORRELATION COEFFICIENT
X
8
3
4
10
6
7
11
Sum 49
Y (X - X ) (Y- Y ) (X –X) (Y-Y )
12
1
0
0
9
-4
-3
12
10
-3
-2
6
15
3
3
9
11
-1
-1
1
12
0
0
0
15
4
3
12
84
0
0
40
y
x
y
12
x
7
n=7
n
n
( x x )( y y )
40
Covariance (XY)
6.67
(n 1)
6
Cov( xy )
6.67
r
0.98
S .d .( x) S .d .( y ) 2.94 X 2.31
nie
nie
SAMPLE SIZE DETERMINATION
nie
SAMPLE SIZE?
• No universal answer
• Assumption-dependent
(and therefore partly subjective)
• Other considerations
(e.g., cost, time-frame, feasibility)
nie
SAMPLING ERROR OF PROPORTION ( 20%)
P = 20%
Sample size (N)
50
100
200
300
400
500
600
700
800
Q = 80%
S.E. =
PQ N
Sampling error of P
5.7
4.0
2.8
2.3
2.0
1.8
1.6
1.5
1.4
1.7
1.2
0.5
0.3
0.2
0.2
0.1
0.1
Note that there is a law of diminishing returns
nie
SAMPLING ERROR OF A MEAN
nie
INFORMATION NEEDED
FOR COMPUTING TRIAL SIZE
1. What is the approximate efficacy of Standard treatment ? = 80%
2. What is the minimum difference that is of practical interest ? = 10%
3. How low should Type I error be ? = 5%
4. How high should the “Power” be ? = 90%
nie
CALCULATION OF TRIAL SIZE
P1
Q1
P2
Q2
Success rate with Standard treatment
Complement (Failures)
Success rate with New treatment
Complement
= 80%
= 20%
= 90%
= 10%
Type I error = 5% (1 - tail) & Power = 90%
Trial size =
PQ PQ
(1600 900)
17.14
17.14
428
P P
10
1
1
2
2
2
1
2
2
Depends upon Type I error & Power
nie
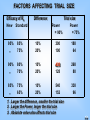
FACTORS AFFECTING TRIAL SIZE
Efficacy of Rx
New Standard
Difference
Trial size
Power
Power
= 90%
= 75%
95%
,,
85%
75%
10%
20%
300
100
188
64
90%
,,
80%
70%
10%
20%
428
128
268
80
85%
,,
75%
65%
10%
20%
540
152
338
96
1. Larger the difference, smaller the trial size
2. Larger the Power, larger the trial size
3. Absolute value also affects trial size
nie
ALTERNATIVE FORMULATIONS
If Standard treatment has 80% efficacy and New treatment is
expected to be at least 10% more effective, for 5% significance level
(1-tail) & 90% Power,
the required trial size is 428
Suppose only 300 cases are available:
1. What is the Power with which a 10% superiority can be detected ?
Ans : 80% Power
2.What is the smallest superiority that can be detected with a Power of 90%?
Ans : 11.6%, i.e., New treatment should have efficacy of at least 91.6%
nie
ALTERNATIVE FORMULATIONS (Continued)
No. of
Detectable
Available superiority
cases
with Power
of 90%
428
10%
300
11.6%
250
12.5%
200
14%
150
15%
Power with which
10% superiority
can be detected
90%
80%
72%
64%
54%
Standard treatment = 80%, Type I error = 5% (1-tail)
nie
CASE - CONTROL STUDY
Hypothesis : Odds ratio of diarrhoea is at least 3 in people who ate
contaminated food as compared to those who did not eat
It is given (assumed) that 30% of people ate contaminated food
Food
Diarrhoea
(CASE)
Contaminated
Not contaminated
Odds ratio =
0.7 P
0.3(1 P )
2
No diarrhoea
(CONTROL)
P2
0.30
1-P2
0.70
1.00
1.00
= 3 ; i.e. P2 = 0.5625
2
Given that P1 = 0.3; P2 = 0.5625; Type I error = 0.05(2-tail); Power = 90%
No. of subjects required = 70 cases & 70 controls
nie
CASE – CONTROL STUDY
Hypothesis : Odds ratio(OR) of diarrhoea is at least 3, in people who ate
contaminated food as compared to those who did not eat
It is known that 30% of people ate contaminated food
Type I error (2-tail) = 5%;
Power = 90%
No. of people to be studied = 70 cases & 70 controls
ALTERNATIVE FORMULATIONS
(a) If only 50 cases are available, what is the Power of detecting
1. A OR of 3 ?
75%
2. A OR of 2 ?
38%
(b) What is the smallest OR that can be detected with 90% Power ?
3.6
nie
ESTIMATING A PROPORTION
USING SIMPLE RANDOM SAMPLING
1. Approximate magnitude of the proportion (P) ?
e.g., Death due to diarrhoea P = 2% [Q = 98%]
2. Limit of accuracy required (L) ?
e.g., 25% of P, i.e., L = 0.5%
3. Degree of confidence required (Z is appropriate factor) ?
e.g., 95% (Z = 1.96)
i.e., the 95% confidence interval should be
(Estimated percentage ± 0.5)
Z PQ
L
2
Required sample size =
2
= 3012
nie
SAMPLE SIZE ESTIMATES
(Simple Random Sample)
MORTALITY
(per 1000)
100
50
20
10
L
N
(±25%)
± 25
553
± 12.5 1168
±5
3012
± 2.5 6085
L
N
(±10%)
± 10 3457
±5
7299
±2
18824
±1
38032
Absolute size of sample is important, not the sampling fraction
nie
TRIAL SIZE FOR DIFFERENCE
BETWEEN TWO MEANS
District A
District B
Mean (m)
s.d. (s)
3000 g
3200 g
500 g
500 g
2( Z Z ) ( S S )
N
(m m )
2
2
2
1
2
2
1
2
(10.5)(500 500 )
2
262
(3200 3000)
2
2
2
Z = 1.96 (5% significance level) Z = 1.28 (Power of 90%)
Larger the difference , smaller the trial size
Greater the Power, greater the trial size
Larger the s.d., greater the trial size
nie
ESTIMATION OF MEAN
WITH REQUIRED DEGREE OF PRECISION
Mean weight = 3000 g
s.d. = 500 g
Required 95% confidence limits = 3000 50
500
2X
50
N
2 X 500
N
400
50
2
nie
ESTIMATION OF DIFFERENCE
BETWEEN TWO PROPORTIONS
District A
District B
Nurses leaving service
30 %
15 %
Required 95% confidence limits 15% 10%
2 (s.e. of difference between proportions) = 10%
s.e = 5%
s.e. of difference between proportions
30 X 70 15 X 85
5 N 135
N
N
Study size = 2 X 135 = 270
nie
ESTIMATION OF DIFFERENCE
BETWEEN TWO MEANS
Group A
Group B
3000 g (m1)
3200 g (m2)
s = 500 g
Degree of precision 50% (L); Confidence factor 1.96 (Z )
2Z S
Sample size in each group(N) =
L% of m m
2
2
2
1
2
2(1.96) 500
N
192
50% of 200
2
2
2
Study size = 2N = 384
nie
OTHER SITUATIONS CONSIDERED
EQUIVALENCE OF TWO TREATMENTS
Demonstrating that two proportions / mean values are equivalent
COMPARISONS ON PAIRED OBSERVATIONS
Demonstrating that the difference (in proportions /mean
values) is significantly different from zero
nie
CONCLUSIONS
1. No stock answer for all situations
2. Initiate dialogue with Applied Statistician
3. Discuss assumptions
- Don’t be rigid
- Consider several possibilities
4. Examine feed-back from Statistician
5. Consider other factors also - Cost, Time, Feasibility
6. Make a balanced choice
7.
Ask if this number gives you a reasonable prospect of coming to conclusion
8. If yes, Sail ahead
9. If No, reformulate your problem for study, and start all over again!!!
nie
nie
CONFIDENCE INTERVALS
nie
“ Excessive use of hypothesis testing at the expense of
other ways of assessing results has reached such a
degree that levels of significance are often quoted alone in
the main text and abstracts of the papers, with no
mention of the actual concentrations, proportions etc. or
other differences”
M.J.Gardner and D.J.Altman - BMJ (1986)
nie
LIMITATION OF P- VALUES
1. Statements
such
as
P < 0.05,
P > 0.05 or
P = Non - Sgt. convey little information about
study’s findings, and encourage over simplistic
interpretation
2. Even exact P-values convey no information about the
size of a difference or the strength of an association
nie
CLINICALLY UNIMPORTANT DIFFERENCES
CAN BE STATISTICALLY SIGNIFICANT
Mean B.P.
S.d.
No.of subjects
Diabetics
Non-diabetics
146 mm Hg
143 mm Hg
10 mm Hg
10 mm Hg
200
200
Difference
= 3 mm Hg
s.e. of difference = 1 mm Hg
t = 3 ; Statistically significant
nie
APPRECIABLE OBSERVED DIFFERENCE
(10%)
CAN BE NON-SIGNIFICANT
BECAUSE OF INADEQUATE TRIAL SIZE
I
II
Trial size
Non-sgt.
Sgt
50% 60% 350
400
60% 70% 300
360
70% 80% 250
300
80% 90% 180
200
nie
DEFINITION OF CONFIDENCE INTERVAL
Suppose, in a sample of 100 observations,
the mean height is 68” and s.d. is 10”
Sampling error of the mean = 10 / 100
=1
95% confidence limits for population mean are 68 1.96 x (1),
i.e. approximately 66” to 70”
In general, the 95% CI for any estimate is {E 1.96 (s.e. of E)}
If sample size (n) is less than 60, 1.96 must be replaced by
appropriate 5% value of t
nie
FINDING OF NON - SIGNIFICANCE
IN A CLINICAL TRIAL
Treatment Success
Failure
Total
A
76 (75%)
25
101
B
51 (66%)
26
77
Chi - square = 1.74; Non - sgt ;
P > 0.1
Difference between A & B = 9%
95% Confidence interval is - 4% to 22%
Compared to B, A is at best an appreciable advantage,
and at worst a slight disadvantage
nie
FINDING OF SIGNIFICANCE
IN A CLINICAL TRIAL
Treatment Success
Failure
Total
A
49 (82%)
11
60
B
33 (60%)
22
55
82
33
115
Total
Chi - square = 6.58; Sgt. at 1% level
Difference between A & B = 22%
95% Confidence interval is 6% to 38%
Changing from B to A can lead to 6% to 38% more patients being cured.
This is more informative than just saying that the treatments are
significantly different
nie
FINDING OF BORDER-LINE SIGNIFICANCE
IN A CLINICAL TRIAL
Isoniazid dose
Fav.
Unfav. Total % Fav. resp.
400 mg x 1
47
17
64
73%
200 mg x 2
38
28
66
58%
2 = 3.61 ; P = 0.06 ; Non-Sgt. ( but border-line)
Difference = 15%
95% CI for difference between treatments is -1% to 31%
This result would suggest that a dosage of 400 mg is more effective
when given once a day than in 2 divided doses of 200 mg
nie
CASE-HOLDING IN TUBERCULOSIS PROGRAMME
Motivation Completed
Failed to
programme treatment
complete
Total
1978 Routine
276 (46%)
324
600
1988 Special
312 (52%)
288
600
Total
588
612
1200
Chi-square = 4.32 ; Sgt. at 5% level
Impact of motivation on case-holding = 6%
95% CI is 0.4% to 11.6%
This is more informative than a significance test, and could well lead
to a decision that the intervention was not worthwhile despite the
statistical significance
nie
FIELD TRIAL OF ANTI- LEPROSY VACCINE
Placebo
BCG
Cases
Non-cases
Total
2896
4555
57104
115445
60,000
120,000
Incidence
(per 1000)
48.3
38.0
P < 0.001; Vaccine efficacy = 21.4 %
95% Confidence Interval is 17.7% to 24.9% (Int. = 7.2%)
Placebo
BCG
290
456
5710
11544
6000
12000
48.3
38.0
P < 0.001; Vaccine efficacy = 21.4 %
95% Confidence Interval is 9.4% to 32.1% (Int. = 22.7%)
nie
LABORATORY ILLUSTRATION –
ELISA TEST FOR HIV
Sensitivity
95% CI
Range
15 / 15
100%
78% - 100%
22%
245 / 254
100%
99% - 100%
1%
nie
EDITORIAL POLICIES ENCOURAGING
USE OF CONFIDENCE INTERVALS
British Medical Journal
1986
American Journal of Public Health
1986
The Annals of Internal Medicine
1986
Lancet
1987
Uniform requirements for manuscripts
submitted to biomedical Journals*
1988
* Prepared by “INTERNATIONAL COMMITTE OF MEDICAL JOURNAL EDITORS”
nie
nie
TEST FOR MEANS
nie
APPLICATION OF t - TEST
– AN ILLUSTRATION
DRUG
A
No of BS – Fasting (mg%)
pts.
Initial
Final
30
178
153
Decrease
P – value
(A vs. B)
25*
> 0.05 (NS)
B
31
179
119
60*
* Statistically Significant ( P < 0.05)
nie
t - TESTS
To test the difference between two sample means
- paired (e.g. before and after treatment )
- matched (e.g. patients matched for Age , Sex , etc)
PAIRED t-Test
- not paired / unmatched
UNPAIRED (independent) t-Test
nie
NUMERICAL EXAMPLE OF PAIRED t - TEST
ESR - 1 hour ( mm)
Square of
Pt. Before Rx
After Rx Difference difference
No.
(a -b=d)
(d2)
(a)
(b)
1
2
3
4
5
6
7
8
9
10
25
43
38
20
41
48
15
28
35
33
8
10
6
7
10
5
8
9
4
3
17
33
32
13
31
43
7
19
31
30
289
1088
1024
169
961
1849
49
361
961
900
Total
326
70
256
7652
nie
d =
256 ;
n
= 10 ;
d = 256/10
=
25.6
d2 = 7652
1 2 ( d ) 2
d
Variance (s2) =
n 1
n
1
(256) 2
7652
= 122.04
=
10 1
10
s = S 2 = 122.04 =
t
=
d
s/n
11.047
25.6
=
= 7.33 with 9 d.f.
11.047 / 10
nie
INFERENCE
Calculated value of t = 7.33 with 9 df
Tabulated value of t(df=9)(0.1%)
= 4.781
tcal > ttab indicating that the treatment had a significant
(P < 0.001) benefit in reducing the ESR
The mean ESR after treatment (7.0 mm) is significantly less
than the mean pre-treatment
ESR value (32.6 mm)
nie
t - TEST ON PAIRED OBSERVATIONS
Number of pairs
=
n
Value before Rx
=
a
Value after Rx
=
b
Difference
=
a -b = d
d =
Mean (d)
Variance
(d)
d
n
2
1
(
d
)
2
2
=s =
d
n 1
n
d 0
d
t =
=
s n
s n
with (n-1) df
nie
NUMERICAL EXAMPLE OF UNPAIRED t - TEST
nie
tcal > t tab indicating that the mean energy expenditure in
obese group (10.3) is significantly (P<0.001) higher than
that of lean group (8.1)
nie
UNPAIRED t - TEST
Sample I
n1
x1
s 21
Size
Mean
Variance
Sample II
n2
x2
s2 2
To test the significance of the difference between the two
sample means, calculate
t=
x1 x2
SE ( x1 x2 )
=
x1 x2
1
2 1
s
n1 n2
(n1 - 1) s21 + (n2 - 1) s22
where s2 = ------------------------------(n1 - 1) + (n2 - 1)
t follows a t distribution with (n1 + n2 - 2) df
nie
ASSUMPTIONS
The underlying assumptions for the unpaired t - test are
1) the distributions of x1 & x2 are Normal &
2) the population variances of x1 & x2 are equal
However, minor deviations from these assumptions do not
affect the validity of the test
nie
UNEQUAL VARIANCES
• Situations are sometimes encountered where the variances in the
two samples differ considerably from one another
• An example of this would be a situation where two technicians, one
experienced (and therefore more consistent ) and the other relatively
inexperienced (and therefore more variable ) undertake a blood count
• Both technicians would be estimating the same population mean
value,but the more experienced one would have a smaller variability
in his readings than the less experienced one
nie
• It is difficult to suggest a definite course of action for all
situations with unequal variances
• Sometimes , a transformation of the values to some other
scale (e.g. logarithmic ) has the effect of equalising the
variances
• When this is not possible, specific methods are available
( e.g. modified t – test , Fisher-Behren’s test)
nie
VARIANCE RATIO TEST ( F- TEST)
To test the equality of two variances, s12 & s22, we use a statistical test
called the ‘variance ratio’ test (F-test)
Calculate the ratio of the larger variance to the smaller variance
s1 2
i.e., F = ---(s12 - larger variance)
s2 2
which follows a F-distribution with (n1 – 1) & (n2 – 1) df
Example :
Variance - Infected group = 10.9
Control group
F
= 5.9
(n1 = 10)
(n2 = 12)
= 10.9 / 5.9 = 1.85 with 9,11 df.
Tabulated F9,11(5%) = 2.92
Fcal < Ftab indicates that the variances are equal
nie
ASSUMPTIONS
•
The two samples must be independent (e.g. two
series of patients and not the same patients tested
twice, before & after treatment)
•
Both samples must have come from a Normal
distribution
nie
UNPAIRED t - TEST ON PAIRED DATA
• It would be inefficient to test paired observations
as though they were unpaired
• In general, it will lead to underestimation of t - value
and hence overestimation of probability value
i.e.,
undercalling of significant difference
nie
t - TESTS
To test the difference
between 2 sample mean values
Two sample values are
Paired / Matched
Two sample values are
Unpaired / Not matched
Check the equality
of variances
Paired
t-Test
Equal
variances
Unequal
variances
Unpaired
t-Test
Modified t-Test /
Fisher-Behren test
nie
REGRESSION
nie
UNIVARIATE REGRESSION
Regression : Method of describing the relationship
between two variables
Use : To predict the value of one variable given the other
nie
SAMPLE DATA SET
Patient No.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Age (X)
45
48
46
45
46
48
46
55
51
56
53
60
53
54
49
Sys BP (Y)
150
153
148
150
147
153
149
159
157
160
158
165
157
158
154
BP = Response (dependent) variable; Age = Predicator (independent) variable
nie
REGRESSION MODEL
We can perform a “regression of BP on age”,
to derive a straight line that gives an estimated value of BP
for any given age.
The general equation of a linear regression line is
Y = a + bX + e
Where,
a = Intercept
b = Regression coefficient
e = Statistical error
nie
CALCULATIONS
Estimated from the observed values of
Age (X) and BP (Y) by least square method
ˆ ( X X )(Y Y ) Co var iance( X ,Y )
2
Variance( X )
X X
ˆ Y bˆX
b gives the change in Y for a unit change in X
a
is the value of Y when X = 0, which may not be meaningful always
nie
TEST OF SIGNIFICANCE FOR b
Null hypothesis : bˆ 0
bˆ 0
.......(1)
Test statistic t =
ˆ
SE (b)
Where,
SE (bˆ)
Y ) 2 b( X X ) 2
2
(n 2) ( X X )
(Y
The value given under(1) follows a t-distribution with (n-2) df
nie
ASSUMPTIONS
1. The relation between the two variables should be linear
2. The residuals should be independent and random
3. The residuals should follow a Normal distribution with
zero mean and constant variance
4. There should not be any measurement error in both the
variables
nie
PRECAUTIONS
1. Adequate sample size should be ensured
2. Prediction should be made within the range of the
observed values. No extrapolation should be attempted
3. The equation Y = a + bX should not be used
to predict X for a given Y
4. Model adequacy should be verified
nie
RESULTS OF REGRESSION ANALYSIS
-------------------------------------------------------------------------------------Ind. variable
Reg Coeff. b̂ SE b̂
t
P-value
-------------------------------------------------------------------------------------Age
1.08
0.08
14.16
< 0.0001
Constant
100.34
-------------------------------------------------------------------------------------R2 = 93.99% 94%
Systolic BP = 100.34 + 1.08 Age
95% CI for b = b ± 1.96 SE(b) = 1.08 ± 1.96 x 0.08
= (0.92, 1.24)
nie
INTERPRETATIONS
1. b̂ 1.08 Change in age by one year results in a change of
1.08 mm Hg in Sys. BP
2. a 100.34 When age = 0, BP = 100.34, which is absurd
3. BP of a 50 year old individual is
100.24 + 1.08 x 50 = 154.34 154 mm Hg
4.R 94% 94% of the variation in BP is explained by age alone
2
nie
MULTIPLE LINEAR REGRESSION
The response variable is expressed as a combination of
several predictor variables
Eg.
PEmax 47.35 0.147 ht. 1.024 wt.
0.147 & 1.024 are regression coefficients for ht. and wt.
Indicate the increase in
PEmax
for
an increase of 1 cm in ht. and 1 kg in wt., respectively
nie
LOGISTIC REGRESSION
Response variable - Presence or absence of some condition
We predict a transformation of the response variable
instead of the actual value of the variable
Data : Hypertension, Smoking (X1) , Obesity(X2) & Snoring (X3)
Which of the factors are predictors of hypertension?
Logit (p) = -2.378 - 0.068 X1 + 0.695 X2 + 0.872 X3
The probability can be estimated for any combination of the three variables
Also, we can compare the predicated probability for different groups,
e.g., Smokers and Non-smokers
nie
nie
Appropriate choice of
significance tests
nie
Choice of a significance test depends on
• nature of data
• design of the study
nie
To test the hypothesis that proportion of children
immunized with oral polio vaccine = 65%
It was found in a random sample of 100
children, the proportion immunized was 57%
Chi-square test
nie
To compare the incidence of toxicity of 2 drugs
A (20%) & B (12%), the drugs were allocated
randomly to two groups of patients
2 x 2 Chi-square test - UNPAIRED
nie
To compare the incidence of toxicity of 2 drugs
A (20%) & B (12%) both drugs were administered
to same group of patients on different occasions
Paired Chi-square test ( McNemar’s test)
nie
To compare the proportion of malnourished
children in 4 different geographic regions
(Viz., 50%, 47%, 31% & 20%)
4 x 2 Chi-square test
nie
To compare the proportion of malnourished
children in four socio - economic groups, viz.,
Economically weaker (40%), Low income (35%)
Middle income (28%) & High income (15%)
Trend Chi-square test
nie
To compare mean serum cholesterol levels
in Males & Females
Independent t-test
nie
To compare mean blood sugar
values before and after treatment
Paired t-test
nie
Comparison of mean BP of
different occupational groups
ANOVA - CRD
nie
BP was recorded for each patient by 4 doctors
To test for the difference in mean BP readings
by the doctors
ANOVA - RBD
nie
Comparison of mean BP readings
among males and females
after adjusting for the age differences
Analysis of Covariance
nie
nie