* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Balanced BSTs
Survey
Document related concepts
Transcript
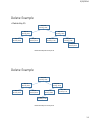
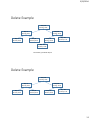
3/22/2014 Balanced Binary Search Trees Balanced Search Trees • Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when implementing a dynamic set of n items. • Examples: • • • • AVL trees 2-3 trees B-trees Red-black trees • Treaps and Randomized Binary Search Trees 1 3/22/2014 Red-black trees • A binary search tree with an extra bit of storage per node: it’s color • Color can be red or black • Tree is approximately balanced such that no path is more than twice as long as any other • Properties: • • • • • Every node is red or black The root is black Leaves are nil nodes that are black If a node is red then both its children are black For each node, all simple paths from the node to descendant leaves contain the same number of black nodes Example of a red-black tree • Every node is red or black • The root is black • Leaves are nil nodes that are black • If a node is red then both its children are black • For each node, all simple paths from the node to descendant leaves contain the same number of black nodes 2 3/22/2014 Height of a red-black tree • Theorem • A red-black tree with n internal nodes (non-nil, nodes with keys) has height h <= 2lg(n+1) • Intuitive argument: Merge red nodes into their black parents Height of a red-black tree • Resulting tree is a 2-3-4 tree where each node has 2, 3, or 4 children • The 2-3-4 tree has uniform depth h’ of leaves 3 3/22/2014 Height of a red-black tree • Since at most half of the leaves on any path are red we must have • h’ >= h/2 • Note that the number of leaves in each tree is n+1 • n+1 >= 2h’ (from the black height of each node) • lg(n+1) >= h’ >= h/2 • h < 2lg(n+1) Corollary • All the query operations take O(lg n) time on a red-black tree with n nodes • • • • • Search Min Max Successor Predecessor • We can also insert and delete in O(lg n) time but it requires some trickier operations to maintain the red-black tree properties • Must change colors and perform rotations 4 3/22/2014 Rotations • A rotation takes O(1) time while maintaining the ordering of the keys and the BST property Insertion Idea • Insert new node as normal to a BST. Color it red and then recolor/rotate up the tree if there are any violations. • Example: Insert x=15 5 3/22/2014 Insertion Example • Recolor 11 to black, 10 to red, the right-rotate 10 with 18 Insertion Example • Recolor, left-rotate 10 with 7 and recolor 6 3/22/2014 Final Tree Analysis • Code is a bit messy with special cases – see textbook for details • Can perform O(1) rotations moving up the tree for O(lg n) insertions • Overall O(lg n) runtime • Deletion also O(lg n) time • Similar special cases to consider 7 3/22/2014 Randomized Data Structures • If we have random input data then we get expected good performance on binary search trees • BUT on particular inputs we can get bad behavior • Idea: • When you can’t randomize the input, randomize the data structure • Gives expected random behavior, which is O(lg n) for BST, on any input! Enter... the TREAP • Tree + Heap, hence TREAP • Both a BST and Heap are merged together. No array like we did previously with the heap, instead it is part of the node of the BST • Invented in 1989 by Aragon and Seidel • Why? • • • • High probability of O(lg n) performance for any input Code is much simpler than red-black trees Perhaps the simplest of all balanced BST’s Can implement without recursion for extra speed 8 3/22/2014 Treap • Treaps maintain a key value and a priority value for each node • binary search tree property maintained for the keys • heap property maintained for the priority value • The heap values are randomly assigned Key: 10 Priority: 0.97 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 15 Priority: 0.85 Key: 8 Priority: 0.15 Key: 12 Priority: 0.12 Key: 85 Priority: 0.76 Key: 97 Priority: 0.11 Treap Insert • Choose a random priority (in our example between 0-1) • Insert like normal into the BST • Rotate up until heap order is restored • Note that rotations preserve the heap property AND the BST property! • Example, insert key=20, priority=0.5 Key: 5 Priority: 0.31 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 4 Priority: 0.13 Key: 8 Priority: 0.15 Key: 2 Priority: 0.24 Key: 4 Priority: 0.13 Key: 8 Priority: 0.15 Key: 20 Priority: 0.5 9 3/22/2014 Insert Example • Rotate Key: 20 Priority: 0.5 Key: 5 Priority: 0.31 Key: 4 Priority: 0.13 Key: 5 Priority: 0.31 Key: 20 Priority: 0.5 Key: 2 Priority: 0.24 Key: 8 Priority: 0.15 Shape of the tree fully specified by random priorities No bad inputs, only bad random numbers! Key: 2 Priority: 0.24 Key: 8 Priority: 0.15 Key: 4 Priority: 0.13 Delete • To delete a node: • • • • Find the node X to delete via BST search If X is a leaf, just delete it If X has only one child, rotate the child up and delete X If X has two children, rotate with child that has the largest priority and then recursively delete X 10 3/22/2014 Delete Example • Delete Key 15 Key: 10 Priority: 0.97 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 15 Priority: 0.85 Key: 8 Priority: 0.15 Key: 12 Priority: 0.10 Key: 85 Priority: 0.76 Key: 97 Priority: 0.11 Rotate with Key 85 Priority 0.76 Delete Example Key: 10 Priority: 0.97 Key: 85 Priority: 0.76 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 8 Priority: 0.15 Key: 15 Priority: 0.85 Key: 97 Priority: 0.11 Key: 12 Priority: 0.10 Rotate with Key 12 Priority 0.10 11 3/22/2014 Delete Example Key: 10 Priority: 0.97 Key: 85 Priority: 0.76 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 8 Priority: 0.15 Key: 12 Priority: 0.10 Key: 97 Priority: 0.11 Key: 15 Priority: 0.85 No children, just delete Key 15 Delete Example Key: 10 Priority: 0.97 Key: 85 Priority: 0.76 Key: 5 Priority: 0.31 Key: 2 Priority: 0.24 Key: 8 Priority: 0.15 Key: 12 Priority: 0.10 Key: 97 Priority: 0.11 12 3/22/2014 Treap Applet • http://www.ibr.cs.tu-bs.de/courses/ss98/audii/applets/BST/TreapExample.html Treap Summary • Implements Binary Search Tree • At a more abstract level, a Dictionary – fast to insert, retrieve, delete • Insert, Delete, and Find in expected O(log n) time • Worst case O(n) but extremely unlikely • Memory use O(1) per node • Relatively simple to implement, much less overhead than red-black or AVL trees 13