Download Balanced BSTs

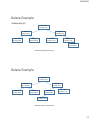
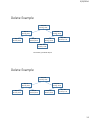
3/22/2014
Balanced Binary Search Trees
Balanced Search Trees
• Balanced search tree: A search-tree data structure for which a height
of O(lg n) is guaranteed when implementing a dynamic set of n items.
• Examples:
•
•
•
•
AVL trees
2-3 trees
B-trees
Red-black trees
• Treaps and Randomized Binary Search Trees
1
3/22/2014
Red-black trees
• A binary search tree with an extra bit of storage per node: it’s color
• Color can be red or black
• Tree is approximately balanced such that no path is more than twice
as long as any other
• Properties:
•
•
•
•
•
Every node is red or black
The root is black
Leaves are nil nodes that are black
If a node is red then both its children are black
For each node, all simple paths from the node to descendant leaves contain
the same number of black nodes
Example of a red-black tree
• Every node is red or
black
• The root is black
• Leaves are nil nodes
that are black
• If a node is red then
both its children are
black
• For each node, all
simple paths from the
node to descendant
leaves contain the
same number of black
nodes
2
3/22/2014
Height of a red-black tree
• Theorem
• A red-black tree with n internal nodes (non-nil, nodes with keys) has height
h <= 2lg(n+1)
• Intuitive argument: Merge red nodes into their black parents
Height of a red-black tree
• Resulting tree is a 2-3-4 tree where each node has 2, 3, or 4 children
• The 2-3-4 tree has uniform depth h’ of leaves
3
3/22/2014
Height of a red-black tree
• Since at most half of the
leaves on any path are
red we must have
• h’ >= h/2
• Note that the number of
leaves in each tree is n+1
• n+1 >= 2h’ (from the black
height of each node)
• lg(n+1) >= h’ >= h/2
• h < 2lg(n+1)
Corollary
• All the query operations take O(lg n) time on a red-black tree with n
nodes
•
•
•
•
•
Search
Min
Max
Successor
Predecessor
• We can also insert and delete in O(lg n) time but it requires some
trickier operations to maintain the red-black tree properties
• Must change colors and perform rotations
4
3/22/2014
Rotations
• A rotation takes O(1) time while maintaining the ordering of the keys
and the BST property
Insertion Idea
• Insert new node as normal to a BST. Color it red and then
recolor/rotate up the tree if there are any violations.
• Example: Insert x=15
5
3/22/2014
Insertion Example
• Recolor 11 to black, 10 to red, the right-rotate 10 with 18
Insertion Example
• Recolor, left-rotate 10 with 7 and recolor
6
3/22/2014
Final Tree
Analysis
• Code is a bit messy with special cases – see textbook for details
• Can perform O(1) rotations moving up the tree for O(lg n) insertions
• Overall O(lg n) runtime
• Deletion also O(lg n) time
• Similar special cases to consider
7
3/22/2014
Randomized Data Structures
• If we have random input data then we get expected good
performance on binary search trees
• BUT on particular inputs we can get bad behavior
• Idea:
• When you can’t randomize the input, randomize the data structure
• Gives expected random behavior, which is O(lg n) for BST, on any input!
Enter... the TREAP
• Tree + Heap, hence TREAP
• Both a BST and Heap are merged together. No array like we did
previously with the heap, instead it is part of the node of the BST
• Invented in 1989 by Aragon and Seidel
• Why?
•
•
•
•
High probability of O(lg n) performance for any input
Code is much simpler than red-black trees
Perhaps the simplest of all balanced BST’s
Can implement without recursion for extra speed
8
3/22/2014
Treap
• Treaps maintain a key value and a priority value for each node
• binary search tree property maintained for the keys
• heap property maintained for the priority value
• The heap values are randomly assigned
Key: 10
Priority: 0.97
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 15
Priority: 0.85
Key: 8
Priority: 0.15
Key: 12
Priority: 0.12
Key: 85
Priority: 0.76
Key: 97
Priority: 0.11
Treap Insert
• Choose a random priority (in our example between 0-1)
• Insert like normal into the BST
• Rotate up until heap order is restored
• Note that rotations preserve the heap property AND the BST property!
• Example, insert key=20, priority=0.5
Key: 5
Priority: 0.31
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 4
Priority: 0.13
Key: 8
Priority: 0.15
Key: 2
Priority: 0.24
Key: 4
Priority: 0.13
Key: 8
Priority: 0.15
Key: 20
Priority: 0.5
9
3/22/2014
Insert Example
• Rotate
Key: 20
Priority: 0.5
Key: 5
Priority: 0.31
Key: 4
Priority: 0.13
Key: 5
Priority: 0.31
Key: 20
Priority: 0.5
Key: 2
Priority: 0.24
Key: 8
Priority: 0.15
Shape of the tree fully specified by random priorities
No bad inputs, only bad random numbers!
Key: 2
Priority: 0.24
Key: 8
Priority: 0.15
Key: 4
Priority: 0.13
Delete
• To delete a node:
•
•
•
•
Find the node X to delete via BST search
If X is a leaf, just delete it
If X has only one child, rotate the child up and delete X
If X has two children, rotate with child that has the largest priority and then
recursively delete X
10
3/22/2014
Delete Example
• Delete Key 15
Key: 10
Priority: 0.97
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 15
Priority: 0.85
Key: 8
Priority: 0.15
Key: 12
Priority: 0.10
Key: 85
Priority: 0.76
Key: 97
Priority: 0.11
Rotate with Key 85 Priority 0.76
Delete Example
Key: 10
Priority: 0.97
Key: 85
Priority: 0.76
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 8
Priority: 0.15
Key: 15
Priority: 0.85
Key: 97
Priority: 0.11
Key: 12
Priority: 0.10
Rotate with Key 12 Priority 0.10
11
3/22/2014
Delete Example
Key: 10
Priority: 0.97
Key: 85
Priority: 0.76
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 8
Priority: 0.15
Key: 12
Priority: 0.10
Key: 97
Priority: 0.11
Key: 15
Priority: 0.85
No children, just delete Key 15
Delete Example
Key: 10
Priority: 0.97
Key: 85
Priority: 0.76
Key: 5
Priority: 0.31
Key: 2
Priority: 0.24
Key: 8
Priority: 0.15
Key: 12
Priority: 0.10
Key: 97
Priority: 0.11
12
3/22/2014
Treap Applet
• http://www.ibr.cs.tu-bs.de/courses/ss98/audii/applets/BST/TreapExample.html
Treap Summary
• Implements Binary Search Tree
• At a more abstract level, a Dictionary – fast to insert, retrieve, delete
• Insert, Delete, and Find in expected O(log n) time
• Worst case O(n) but extremely unlikely
• Memory use O(1) per node
• Relatively simple to implement, much less overhead than red-black or
AVL trees
13