* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 3 Notes
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Contour line wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Perspective (graphical) wikipedia , lookup
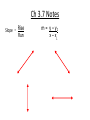
Chapter 3.1 Common Core G.CO.1 & G.CO.9 Know precise definitions of…parallel line. Prove theorems about lines and angles. Objectives – To identify relationships between figures in space. To identify angles formed by two lines and a transversal. Ch 3.1 Notes Parallel Lines – 2 lines that do not intersect and are coplanar Parallel Planes – 2 planes that do not intersect Skew Lines – 2 lines that do not intersect and are not coplanar Identifying Angles Formed by Transversals Transversal – is a line that intersects 2 or more coplanar lines at different points. Transversal Corresponding Angles Alternate Interior Angles Alternate Exterior Angles Consecutive Interior Angles (Same-Side Int. Angles) 1 2 3 4 5 6 7 8 Chapter 3.2 Common Core G.CO.9 Prove theorems about lines and angles. Theorems include…when a transversal crosses parallel lines, alternate interior angles are congruent. Objectives – To prove theorems about parallel lines. To use properties of parallel lines to find angles measures. Ch 3.2 Notes Corresponding ∠ Thm Alt. Int. ∠ Thm Alt. Ext. ∠ Thm Same-Side Int. ∠ Post. (Consecutive Int. Post.) Chapter 3.3 Common Core G.CO.9 Prove theorems about lines and angles. Theorems include…when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent. Objective – To determine whether two lines are parallel. Ch 3.3 Notes Four ways to prove two lines are parallel. 1) Show Corr. ∠’s are ≌ 2) Show Alt. Int. ∠’s are ≌ 3) Show Alt. Ext. ∠’s are ≌ 4) Show Same Side are Supp. (Cons. Int. ∠’s are supp.) Flow Proof – is another way of proving something by using arrows and logically connections between statements Chapter 3.4 Common Core Common Core G.MG.3 Apply geometric methods to solve design problems. Objective – To relate parallel and perpendicular lines. Ch 3.4 Notes Thm – If 2 lines are parallel to the same line then they are parallel to each other. p q r * If p II q and q II r, then p II r. Thm – In a plane, if 2 lines are perpendicular to the same line, then they are parallel to each other. * If m ⊥ p and n ⊥ p, then m II n. Perpendicular Transversal Thm – If a transversal is perpendicular to one of 2 parallel lines, then it is perpendicular to the other. If then Chapter 3.5 Common Core Common Core G.CO.10 Prove theorems about triangles…measures of interior angles of a triangle sum to 180 degrees. Objectives – To use parallel lines to prove a theorem about triangles. To find measures of angles of triangles. Ch 3.5 Notes Triangle Angle-Sum Theorem – the sum of the measures of the angles of a triangle is 180. Triangle Exterior Angle Theorem – the measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles Parallel Postulate – If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line. If then Chapter 3.6 Common Core G.CO.12 & G.CO.13 Make formal geometric constructions with a variety of tools and methods…constructing perpendicular lines…and constructing a line parallel to a given line through a point not on the line. Objective – To construct parallel and perpendicular lines. Ch 3.6 Notes Constructing Parallel Lines Construct a Special Quadrilateral with one pair of parallel sides. Construct a Perpendicular at a Point on the Line Perpendicular Postulate – If there is a line and a point not on the line then there is exactly one line through the point and perpendicular to the given line If then Construct a Perpendicular form a Point to Line Chapter 3.7 Common Core G.GPE.5 Prove the slope criteria for parallel and perpendicular lines. Objective – To graph and write linear equations. Ch 3.7 Notes Slope = Rise Run m = y – y1 x – x1 Slope-intercept Form – y = mx + b where m is the slope and b is the y-intercept Point-Slope Form – y – y1 = m(x – x1) where m is the slope and (x1,y1) is the point Chapter 3.8 Common Core G.GPE.5 Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems. Objective – To relate slope to parallel and perpendicular lines. Ch 3.8 Notes 2 Lines are Parallel to each other if they have the same slope. Ex. m = -4 and m1 = -4 2 Lines are Perpendicular to each other if their slopes are negative reciprocals of each other. Ex. m = 2/3 and m1 = -3/2 then they would be perpendicular lines