* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download undergraduate celestial co
Dyson sphere wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Geocentric model wikipedia , lookup
Reflecting instrument wikipedia , lookup
Observational astronomy wikipedia , lookup
Equation of time wikipedia , lookup
Astronomy in the medieval Islamic world wikipedia , lookup
Archaeoastronomy wikipedia , lookup
History of astronomy wikipedia , lookup
Astronomical unit wikipedia , lookup
Timeline of astronomy wikipedia , lookup
Air mass (astronomy) wikipedia , lookup
Theoretical astronomy wikipedia , lookup
Constellation wikipedia , lookup
Epoch (astronomy) wikipedia , lookup
Chinese astronomy wikipedia , lookup
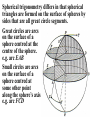
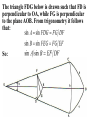
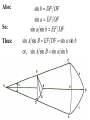
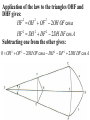
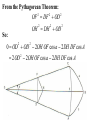
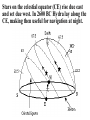
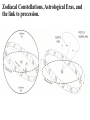
Astronomy 2100 Foundations of Astrophysics (Astronomy Basics) Examine directly observable quantities for stars, such as their positions on the celestial sphere and the light they emit. Topics include properties of the celestial sphere, time-keeping, astronomical catalogues, the two-body problem, dynamics of star clusters, emission and absorption lines in stellar spectra, and the operation of telescopes. Training in the use of the Burke-Gaffney Observatory is done in conjunction with assigned observing projects. 1. The Celestial Sphere Goals: 1. Gain familiarity with the basic equations of spherical astronomy and how they are used for establishing astronomical coordinate systems. 2. Tackle problems in practical astronomy involving timekeeping and star positions. 3. Introduce a bit of archeoastronomy, and the origin of the constellations. Spherical Astronomy: Recall triangles in plane trigonometry. A, B, and C denote angles a, b, and c denote opposite sides Interrelated through: Spherical trigonometry differs in that spherical triangles are formed on the surface of spheres by sides that are all great circle segments. Great circles are arcs on the surface of a sphere centred at the centre of the sphere. e.g. arc EAB Small circles are arcs on the surface of a sphere centred at some other point along the sphere’s axis. e.g. arc FCD The triangle PAB is a spherical triangle. The triangle PCD is not, as illustrated, since the side CD is a small circle. PCD becomes a spherical triangle if the points C and D are connected by a great circle rather than a small circle. The triangle ABC at left is a spherical triangle. Its sides a, b, and c are angles like A, B, and C, in this case the arc lengths subtended by identical angles a, b, and c at the centre of the sphere, a = rsphere cos a = cos a, when rsphere = 1. By definition, no side of a spherical triangle can exceed 180 = π radians. Angles in a spherical triangle denote the angles between two planes that form the sides of the triangle. The surface area of a spherical triangle is denoted as Δ. If θ is the angle between two great circles on the surface of a sphere, then the surface area enclosed by the angle θ is S(θ). If θ = π, then S(π) must encompass the entire area of the sphere, i.e S(π) = 4π. In general, S(θ) = 4θ. When the area Δ is demarked, it can be noted that the sum S(A) + S(B) + S(C) covers the entire surface of the sphere, and also covers the area Δ six times. Thus, S(A) + S(B) + S(C) = 4π + 4Δ. Thus, 4A + 4B + 4C = 4π + 4Δ or Δ=A+B+C–π So the sum of the angles in a spherical triangle must exceed 180 = π, otherwise it would have no area Δ. The basic formulae of spherical trigonometry can be derived in several ways. The most concise is that of Birney in Observational Astronomy, who considers spherical triangles from the perspective of how they are connected to the centre of the sphere. Consider the triangle ABC below, with sides a, b, and c opposite the angles A, B, and C. The triangle FDG below is drawn such that FD is perpendicular to OA, while FG is perpendicular to the plane AOB. From trigonometry it follows that: So: Also: So: Thus: The same type of analysis can be applied to derive relationships involving the angle C and side c. The general formula that applies is written: sin A sin a sin B sin b sin C sin c which is the sine formula of spherical trigonometry. Memory Aid: sine angle/sine opposite side = sine angle/sine opposite side The fundamental formula of spherical trigonometry is derived in different fashion. In the spherical triangle ABC the centre of the sphere is again located at O. Points D, F, and H are the vertices of a triangle oriented in such a way that the sides DF and DH are perpendicular to OA. Note the difference from the previous diagram. As drawn, the angle FDH is equal to the angle A. Recall the cosine law from trigonometry, namely: a 2 b 2 c 2 2bc cos A Application of the law to the triangles OHF and DHF gives: 2 2 2 HF OH OF 2OH OF cos a HF 2 DH 2 DF 2 2DH DF cos A Subtracting one from the other gives: 0 OH 2 OF 2 2OH OF cos a DH 2 DF 2 2DH DF cos A From the Pythagorean Theorem: 2 2 2 OF DF OD OH 2 DH 2 OD 2 So: 0 OD OD 2OH OF cos a 2 DH DF cos A 2 2 2 OD 2OH OF cos a 2 DH DF cos A 2 The equation can be solved for cos a by rearrangement and substitution, namely: cos a OD OD OH OF DF DH OH OF cos A OD OF OD OH DF OF DH OH cos A cos b cos c sin b sin c cos A The resulting formula, referred to as the fundamental formula of spherical trigonometry, is written: cos a cos b cos c sin b sin c cos A Memory Aid: cosine side = cosine adjacent side×cosine adjacent side + sine adjacent side×sine adjacent side×cosine enclosed angle There are two other formulae that can be derived, although their derivation can be found in Smart’s Spherical Astronomy. It is much less involved to simply state them: sin a cos B cos b sin c sin b cos c cos A Smart' s Formula C cos a cos C sin a cot b sin c cot B Four Parts Formula One can usually solve most problems in spherical astronomy using only the sine and cosine formulae. The usefulness of such formulae becomes evident when one considers how they are applied to astronomical co-ordinate systems. Astronomical Co-ordinate Systems: All co-ordinate systems constructed on spheres are defined by a fundamental great circle (FGC) and a reference point (RP) on the FGC. All co-ordinates are angles measured: (i) between great circles perpendicular to the FGC, or (ii) between small circles parallel to the FGC. The FGC has two poles, and the RP is defined in a variety of ways, which accounts for slight differences from one system to another. Terrestrial Co-ordinates. FGC = Earth’s equator, with poles the North Pole and South Pole. RP = crossing point of equator by the Greenwich meridian. Co-ordinates: Longitude = angle measured east and west from the Greenwich meridian. Longitude meridians are great circles. Latitude = measured north and south (not plus or minus) from the Equator. Latitude parallels are small circles. Examples: Halifax. 63º 36'.0 W, 44º 36'.0 N Vancouver. 123º 04'.2 W, 49º 09'.0 N Problem in terrestrial co-ordinates. What is the great circle distance between Halifax and Vancouver, given Earth’s mean radius of 6371 km? Solution: Sketch the situation with known terms. 12304'.2 90– 4909'.0 6336'.0 90 4436'.0 The corresponding spherical triangle can be solved for the angular distance d using the cosine law: cos a cos b cos c sin b sin c cos A or, here : cos d cos 4051' cos 45 24' sin 4051' sin 45 24' cos 59 28' .2 0.75642450.702153 0.65408090.7120260.5079894 0.5311257 0.2365821 0.7677078 d cos 1 0.7677078 39.851501 The great circle distance is R d(radians) = 6371 km (39.851501 × π/180) = 6371 km × 0.6955399 = 4431 km Horizon System. FGC = horizon, with poles the zenith and nadir. RP = north point. Co-ordinates: azimuth = angle measured through east from 0º to 360. Azimuth circles are great circles. altitude = measured from horizon towards zenith (positive) or nadir (negative) from +90º to –90º. Alternate: zenith distance, z = 90º – altitude. Meridian = NS line running through zenith. Prime vertical = EW line running through zenith. Use. Airport runways are designated by azimuth 10°, i.e. runway 33 aligns along azimuth 330°. Air mass, for correction of photometry, is calculated from z. h = height of plain parallel atmosphere = 1.0 X = h/cos z = h sec z = sec z (1 0.0012 tan2z) (better) Photometry from ground level always needs to be corrected for extinction within the Earth’s atmosphere, which increases with decreasing wavelength, i.e. k ~ 1/λ4. m m0 = k sec z = kX where k = extinction coefficient Earth’s atmosphere also refracts light with a wavelength dependence, again in proportion to z. = actual zenith distance. z = observed zenith distance. Then: sin = 1.00029 sin z Denote: R = z, the angle of refraction. Typically, R ≈ 60".29 tan z (undefined at z = 90°) The refraction at the horizon is denoted as horizontal refraction, and amounts to R ≈ 33'. i.e. For z = 90°, = 90° 33'. Equatorial System. FGC = celestial equator (CE, projection on the sky of Earth’s equator), with poles the north and south celestial poles, NCP and SCP. RP = intersection point of meridian with CE (observer-oriented), or vernal equinox γ (skyorinted). Co-ordinates: declination = angle measured north or south of CE from 0º to +90 and 90° (δ). hour angle = angle measured west of meridian (HA), or right ascension = angle measured eastward from vernal equinox (RA). HA and RA are measured in temporal units and are equivalent to angles. On the celestial equator: 1h = 15°, 1m = 15', and 1s = 15″, with the equalities changing by cos δ with increasing declination. Because of their link to timekeeping, HA and RA are tied directly to sidereal (star) time and apparent solar time. Sidereal time (SidT)= HA(γ) Apparent solar time = HA() + 12h Now, HA(γ) = HA(*) + RA(*) = HA() + RA() Thus, SidT = HA() + RA() = Apparent solar time 12h + RA() RA() and δ() during the year are defined by the apparent motion of the Sun in the sky along the ecliptic = Sun’s apparent path, and can be calculated directly or from tables. Useful values: Vernal Equinox, March 20: RA() = 0h, δ() = 0° Summer Solstice, June 21: RA() = 6h, δ() = +23½° Autumnal Equinox, September 23: RA() = 12h, δ() = 0° Winter Solstice, December 22: RA() = 18h, δ() = 23½° The actual dates of the equinoxes and solstices slowly change with time. They were March 25, June 25, September 25, and December 25 when Julius Caesar modified the original Roman calendar system (Julian Calendar) in 46 BC. annual insolation For many problems it is useful to link the horizon and celestial systems using the polar triangle. Interrelationships between the systems are useful for identifying objects in the sky with points on the celestial sphere or for determining when specific objects will be at certain points in the sky. Note that the cosine law relates the parameters through: cos z* = cos(90°φ) cos(90°δ*) + sin(90°φ) sin(90°δ*) cos HA* , or cos z* = sin φ sin δ* + cos φ cos δ* cos HA* where φ is the observer’s latitude on Earth. Some examples. 1. Suppose φ = 30°N and Betelgeuse crossed the meridian 2½ hours ago. How far is it from the zenith? Solution: Input data: φ = +30° δ(Betelgeuse) = +7° 24' = 7°.4 HA* = 2½h = 2h 30m = 37°.5 cos z* = sin30° sin7°.4 + cos30° cos7°.4 cos37°.5 = (0.50.1287956) + (0.86602540.99167110.7933533) = 0.0643978 + 0.6813416 = 0.7457394 z* = cos1(0.7457394) = 41°.8 So Betelgeuse lies almost 42° from the zenith when it is 2½ hours past the meridian at a terrestrial latitude of +30°. Thought question: How would the answer change if the observer was located at 30°S rather than N? 2. For how many hours can an observer at 30°N observe Betelgeuse when its z ≤ 60°? (Since sec 60° = 2, the situation corresponds to X ≤ 2.) Solution: The problem is to obtain Betelgeuse’s HA for z = 60° and double it to get the requested quantity. Inverting the standard equation gives: cos HA* = (cos z* sin φ sin δ*) / cos φ cos δ* = (cos 60° sin 30° sin 7°.4) / cos 30° cos 7°.4 = (0.5 0.50.1287956) / (0.86602540.9916711) = 0.4356022/0.8588123 = 0.5072146 HA* = cos1(0.5072146) = 59°.521524 15°/h = 3h.9681016 = 3h 58m Betelgeuse has X ≤ 2 for 2 3h 58m = 7h 56m. 3. Observations from Arecibo’s radio telescope (18°N) can only be made for objects with z ≤ 20°. If an observer wishes to observe a galaxy with δ = +28°, for how long can it be tracked? Solution: Input data: φ = +18°, and from the last question, cos HA* = (cos z* sin φ sin δ*) / cos φ cos δ* = (cos 20° sin 18° sin 28°) / cos 18° cos 28° = (0.9396926 0.30901690.4694715) / (0.95105650.8829475) = 0.7946179/0.8397329 = 0.9462746 HA* = cos1(0.9462746) = 18°.866497 15°/h = 1h.2577665 = 1h 15m The galaxy can be observed for 21h 15m = 2h 30m. 4. When is the best time of year to observe the stars of Orion, RA = 5½h? Solution: The optimum time for observing any object is when it lies on the observer’s meridian at local midnight, which corresponds to 0h local apparent solar time (LAST). i.e. LAST = HA() + 12h = 0h (midnight) So HA() = 0h 12h = 24h 12h = 12h Orion is then on the meridian, so local sidereal time = HA* = 5½h = HA() + RA() RA() = 5½hHA() = 5½h12h = 29½h12h = 17½h The Sun is at RA = 17½h approximately one week prior to the winter solstice, i.e. around Dec. 15. Ecliptic System. FGC = ecliptic, with poles the north and south ecliptic poles, NEP and SEP. RP = vernal equinox γ. Co-ordinates: celestial (or ecliptic) longitude, λ = angle measured eastward from γ from 0º to 360. celestial (or ecliptic) latitude, β = angle measured from ecliptic. The system is useful for studies of solar system objects. Galactic System. FGC = Galactic equator (GE), defined by the Milky Way, with poles the north and south Galactic poles, NGP and SGP. RP = direction to the Galactic centre (GC), defined by Sgr A*. Co-ordinates: Galactic longitude, l = angle measured Eastward from GC from 0º to 360. Galactic latitude, b = angle measured north or south of GE from 0º to +90 and 90°. Timekeeping. Apparent solar time is defined by the passage of the Sun across the sky, but civil time is more closely related to the motion of the mean Sun, a fictitious object, across the sky. Mean solar time = HA(mean Sun) + 12h The mean Sun differs from the true Sun in the following way. The true Sun travels along the ecliptic at a rate that varies according to the distance of Earth from the Sun. The mean Sun travels along the celestial equator at a uniform rate. Additional complications arise from the use of time zones and daylight saving time. The year length varies according to the calendar system, which has changed from lunar calendars, through luni-solar calendars, to solar calendars, such as the Julian Calendar, Gregorian Calendar, and current modified Gregorian Calendar. Variable star studies normally cite observations according to the Julian Date, JD, measured as the number of sequential days from noon, UT, on January 1, 4713 BC (named by Joseph Scaliger after his father Julius Scaliger), or, better yet, HJD = Heliocentric Julian Date (corrected to the barycentre of the solar system). Another term, modified Julian Date, MJD = JD 2400000.5, is occasionally used. Precession of the Equinoxes. The Earth’s axis of rotation precesses about the perpendicular to the ecliptic as a consequence of the gravitational influences of the Sun and the Moon, but not in the fashion implied by the Wikipedia figure at right. The sense of precession is actually opposite the sense of the Earth’s rotation. A top’s precession. The effects of precession on the location of the north celestial pole (NCP) in the sky. Note that the NCP was located near the bright star Thuban circa 2700 BC, when the pyramids were constructed (see textbook), and was at one time located near Vega, a name that means “fallen,” possibly because it has fallen from its location near the NCP over the years. Precession affects the location of the vernal equinox γ on the celestial sphere, since the celestial equator moves as a result of the gradual realignment of the axis defined by the NCP and SCP. The location of γ regresses along the ecliptic, resulting in a constant increase in a star’s RA, and comparable effects in DEC. The changes can be expressed as: Δα = M + N sin α tan δ Δδ = N cos α where M = 1°.2812323T + 0°.0003879T2 + 0°.0000101T3 N = 0°.5567530T 0°.0001185T2 0°.0000116T3 and T = (t 2000.0)/100, with t the current date in year fractions. See example in textbook. Archaeoastronomy. Many constellations bear names originating from eras when the stellar configuration bore some resemblance to the object after which they are named, e.g. Ursa Major, the Great Bear. Some were named for other reasons, e.g. Hydra. Stars on the celestial equator (CE) rise due east and set due west. In 2600 BC Hydra lay along the CE, making then useful for navigation at night. Only 50 of the 88 modern constellations were known in antiquity. They also outlined only regions in the northern sky, most being named by ancient Minoans. Ancient star maps. Zodiacal Constellations, Astrological Eras, and the link to precession. The Taurus and Aries Eras. The Beginnings? The Gemini Era. The present. The old constellation of Argo, the Ship, was very large. It was but one of many symbols associated with the story of Noah’s Ark. The Summer Triangle Groups that look like their namesakes. Hercules Normally pictured holding the world. Sagittarius An archer? Better pictured as a teapot. The Perseus Group A story in the stars. Ursa Major Does this group truly look like a bear??! Stars are presently designated in a variety of ways: Greek letters, from east to west for stars of comparable brightness (UMa)… Greek letters, from from brightest to faintest for stars of comparable brightness (Ori, Cas), as well as Bayer-Flamsteed numbers… and catalogue numbers. Something different: the General Catalogue of Variable Stars. All such catalogues are available on-line these days. http://cdsarc.u-strasbg.fr/cats/Cats.htx