Download The Golden Mean (Part 1)

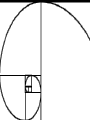
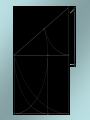
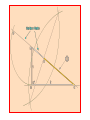
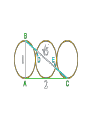
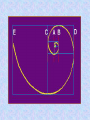
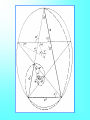
The most beautiful thing we can experience is the
mysterious. It is the source of all true art and science.
-- Einstein, What I Believe
Like God, the Divine Proportion is
Without mathematics
there istono
art.
always similar
itself.
-- Fra Luca Pacioli
Ubi materia, ibi geometria (Where there is matter, there is
geometry)
-- Johannes Kepler
The
Golden
Mean
The
Part I:
Tiny Geometries
Golden
Mean
Shape
Geometry
Construction
3 sides:
Triangle
Insert an equilateral
triangle
inside a circle.
Find the midpoints
of the two sides at A
and B.
Extend the line to the
circle.
The ratio of AB to BG
is Phi.
4 sides:
Square
Insert a square
inside a semi-circle.
The ratio of AB to BG
is Phi.
Take three golden rectangles and assemble them
at 90 degree angles to get a 3D shape with 12
corners:
Click on the shape below and the print the page to
do it yourself:
This is the basis for two geometric solids
The 12 corners become the 12 centers of each of
the 12 pentagons that form the faces of a
dodecahedron.
The 12 corners can also become the 12 points of
each of the 20 triangles that form the faces of a
icosahedron.
Solid
Dodecahedron
Icosahedron
Face shape
Pentagon
Triangle
Faces
12
20
Points
20
12
Edges
30
30
Leonardo Fibonacci’s rabbit reproduction matrix
Month
Rabbits fro m A:
from B:
from C:
D:
B1:
Total
0
A
1
1
A
1
2
A
B
3
A
B
C
4
A
B
C
D
5
A
B
C
D
E
6
A
B
C
D
E
etc.
1
2
3
4
5
2
3
B1
5
B1
B2
C1
8
F
B1
B2
B3
C1
C2
D1
B11
13
6
7
8
9
10
11
12
13
etc.
The Fibonacci Sequence is:
1-1-2-3-5-8-13-21-34-55-89-144-233-377-610-etc.
The Phi Ratio =
1.6180339......
Phi Ratio =
1.6180339......
13 divided by 8 =
1.6250000......
Phi Ratio =
1.6180339......
21 divided by 13 =
1.615384........
Phi Ratio =
1.6180339......
34 divided by 21 =
1.619048........
Phi Ratio =
1.6180339......
55 divided by 34 =
1.617647........
Phi Ratio =
1.6180339......
89 divided by 55 =
1.618182........
Phi Ratio =
1.6180339......
144 divided by 89
=
1.617978........
Phi Ratio =
1.6180339......
233 divided by 144
=
1.618056........
Phi Ratio =
1.6180339......
377 divided by 233
=
1.618026........
Phi Ratio =
1.6180339......
The Fibonacci series has a pattern that repeats every 24
Example: 2,584 numbers
2+5+8+4=19 1+9=10 1+0=1
Numeric reduction is a technique used in analysis of numbers in which all
a number0are added
0 the digi ts of 0
0 together un til o nly one digit r emains. As
an example, the numeric reduction of 256 is 4 because 2+5+6=13 and
1 1+3=4.
1
1
1
233
8
8
8
1 Apply ing numeric
1
1
377
to1the Fibonacci series produces an infinite
reduction
17
8
8
610
7
7
7
1, 1,3 2, 3, 5, 8,
3 4, 3, 7,31, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
987
24
6
6
4
4
10
1
2
3
series of 24 re peating digits:
2
2
2
5 If you take the
5 first 12
5 digi ts and
5
add them to the second twelve digits and
1,597 22
apply num eric reduction to the result, you find that they all have a value of
8 9.
8
8
8
2,584 19
13
21
34
55
89
4
1st 12 numbers
3
2nd 12 numbers
7
4
4
3
3
7
7
Numeric reduction - Add rows 1
10
1
1
and 2
17
8
1
1
2
3
5
8
4
3
1 8 14 9
7 4,181
5
5
8
8
7
6
4
1
5
6
8 1 24 9
2 6,765
6
6
9
9
9
9
9
9
9
9
10,946 20
9 9 9 18
17,711 17
2
2
8
8
9 9 28 9 10
9
28,657
1
8
Final nu meric reduction - Add
144 digit s of result
9
9
9
9
9
9
9
9
9
9
9
46,368
27
9
9
The Fibonacci Series is found in Pascal's Triangle
Pascal's Triangle, developed by the French Mathematician Blaise
Pascal, is formed by starting with an apex of 1. Every number
below in the triangle is the sum of the two numbers diagonally
above it to the left and the right, with positions outside the triangle
counting as zero.
The numbers on diagonals of the triangle add to the Fibonacci
series:
Pascal's triangle has many unusual properties and a variety of uses:





Horizontal rows add to powers of 2 (i.e., 1, 2, 4, 8, 16, etc.)
The horizontal rows represent powers of 11 (1, 11, 121, 1331, etc.)
Adding any two successive numbers in the diagonal 1-3-6-10-15-21-28...
results in a perfect square (1, 4, 9, 16, etc.)
It can be used to find combinations in probability problems (if, for instance,
you pick any two of five items, the number of possible combinat ions is 10,
found by looking in the second place of the fifth row. Do not count the 1's.)
When the first number to the right of the 1 in any row is a prime number, all
numbers in that row are divisible by that prime number
n
Phi n
0
1.000000
1
1.618034
2
2.618034
3
4.236068
4
6.854102
5 11.090170
6 17.944272
n n
n
Phi
Phin
n
1/ Phi
1/Phi n
n n
n
PhiPhi
- 1/Phi
+ 1/Phi n
0 1
1.618033989
0.618033989
1.000000000
1.000000000
1 2
2 3
2.618033989
0.381966011
4.236067977
0.236067977
4 3
4 5
6.854101966
0.145898034
11.090169944
0.090169944
11 7
6 7
17.944271910
0.055728090
29.034441854
0.034441854
2918
8
9
10
11
46.978713764
0.021286236
122.991869381
0.008130619
76.013155617
199.005024999
0.013155617
0.005024999
76
47
123
199
© 2006 by Albireo Blossoms
Productions, Ltd.
All rights
reserved.