* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The Golden Mean (Part 1)
Positional notation wikipedia , lookup
Location arithmetic wikipedia , lookup
Mathematics and art wikipedia , lookup
Mathematics and architecture wikipedia , lookup
Elementary mathematics wikipedia , lookup
Golden ratio wikipedia , lookup
List of works designed with the golden ratio wikipedia , lookup
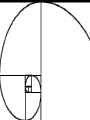
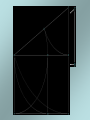
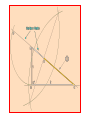
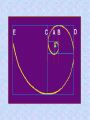
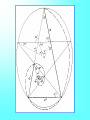
The most beautiful thing we can experience is the mysterious. It is the source of all true art and science. -- Einstein, What I Believe Like God, the Divine Proportion is Without mathematics there istono art. always similar itself. -- Fra Luca Pacioli Ubi materia, ibi geometria (Where there is matter, there is geometry) -- Johannes Kepler The Golden Mean The Part I: Tiny Geometries Golden Mean Shape Geometry Construction 3 sides: Triangle Insert an equilateral triangle inside a circle. Find the midpoints of the two sides at A and B. Extend the line to the circle. The ratio of AB to BG is Phi. 4 sides: Square Insert a square inside a semi-circle. The ratio of AB to BG is Phi. Take three golden rectangles and assemble them at 90 degree angles to get a 3D shape with 12 corners: Click on the shape below and the print the page to do it yourself: This is the basis for two geometric solids The 12 corners become the 12 centers of each of the 12 pentagons that form the faces of a dodecahedron. The 12 corners can also become the 12 points of each of the 20 triangles that form the faces of a icosahedron. Solid Dodecahedron Icosahedron Face shape Pentagon Triangle Faces 12 20 Points 20 12 Edges 30 30 Leonardo Fibonacci’s rabbit reproduction matrix Month Rabbits fro m A: from B: from C: D: B1: Total 0 A 1 1 A 1 2 A B 3 A B C 4 A B C D 5 A B C D E 6 A B C D E etc. 1 2 3 4 5 2 3 B1 5 B1 B2 C1 8 F B1 B2 B3 C1 C2 D1 B11 13 6 7 8 9 10 11 12 13 etc. The Fibonacci Sequence is: 1-1-2-3-5-8-13-21-34-55-89-144-233-377-610-etc. The Phi Ratio = 1.6180339...... Phi Ratio = 1.6180339...... 13 divided by 8 = 1.6250000...... Phi Ratio = 1.6180339...... 21 divided by 13 = 1.615384........ Phi Ratio = 1.6180339...... 34 divided by 21 = 1.619048........ Phi Ratio = 1.6180339...... 55 divided by 34 = 1.617647........ Phi Ratio = 1.6180339...... 89 divided by 55 = 1.618182........ Phi Ratio = 1.6180339...... 144 divided by 89 = 1.617978........ Phi Ratio = 1.6180339...... 233 divided by 144 = 1.618056........ Phi Ratio = 1.6180339...... 377 divided by 233 = 1.618026........ Phi Ratio = 1.6180339...... The Fibonacci series has a pattern that repeats every 24 Example: 2,584 numbers 2+5+8+4=19 1+9=10 1+0=1 Numeric reduction is a technique used in analysis of numbers in which all a number0are added 0 the digi ts of 0 0 together un til o nly one digit r emains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1 1+3=4. 1 1 1 233 8 8 8 1 Apply ing numeric 1 1 377 to1the Fibonacci series produces an infinite reduction 17 8 8 610 7 7 7 1, 1,3 2, 3, 5, 8, 3 4, 3, 7,31, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9 987 24 6 6 4 4 10 1 2 3 series of 24 re peating digits: 2 2 2 5 If you take the 5 first 12 5 digi ts and 5 add them to the second twelve digits and 1,597 22 apply num eric reduction to the result, you find that they all have a value of 8 9. 8 8 8 2,584 19 13 21 34 55 89 4 1st 12 numbers 3 2nd 12 numbers 7 4 4 3 3 7 7 Numeric reduction - Add rows 1 10 1 1 and 2 17 8 1 1 2 3 5 8 4 3 1 8 14 9 7 4,181 5 5 8 8 7 6 4 1 5 6 8 1 24 9 2 6,765 6 6 9 9 9 9 9 9 9 9 10,946 20 9 9 9 18 17,711 17 2 2 8 8 9 9 28 9 10 9 28,657 1 8 Final nu meric reduction - Add 144 digit s of result 9 9 9 9 9 9 9 9 9 9 9 46,368 27 9 9 The Fibonacci Series is found in Pascal's Triangle Pascal's Triangle, developed by the French Mathematician Blaise Pascal, is formed by starting with an apex of 1. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero. The numbers on diagonals of the triangle add to the Fibonacci series: Pascal's triangle has many unusual properties and a variety of uses: Horizontal rows add to powers of 2 (i.e., 1, 2, 4, 8, 16, etc.) The horizontal rows represent powers of 11 (1, 11, 121, 1331, etc.) Adding any two successive numbers in the diagonal 1-3-6-10-15-21-28... results in a perfect square (1, 4, 9, 16, etc.) It can be used to find combinations in probability problems (if, for instance, you pick any two of five items, the number of possible combinat ions is 10, found by looking in the second place of the fifth row. Do not count the 1's.) When the first number to the right of the 1 in any row is a prime number, all numbers in that row are divisible by that prime number n Phi n 0 1.000000 1 1.618034 2 2.618034 3 4.236068 4 6.854102 5 11.090170 6 17.944272 n n n Phi Phin n 1/ Phi 1/Phi n n n n PhiPhi - 1/Phi + 1/Phi n 0 1 1.618033989 0.618033989 1.000000000 1.000000000 1 2 2 3 2.618033989 0.381966011 4.236067977 0.236067977 4 3 4 5 6.854101966 0.145898034 11.090169944 0.090169944 11 7 6 7 17.944271910 0.055728090 29.034441854 0.034441854 2918 8 9 10 11 46.978713764 0.021286236 122.991869381 0.008130619 76.013155617 199.005024999 0.013155617 0.005024999 76 47 123 199 © 2006 by Albireo Blossoms Productions, Ltd. All rights reserved.