* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 3 Kinetics of Particles
Hunting oscillation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Internal energy wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
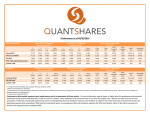
Chapter 3 Kinetics of Particles 2103-212 Dynamics, NAV, 2012 1 3-2 Work and Energy 2103-212 Dynamics, NAV, 2012 2 3-2. Work and Energy 1. Work and Kinetic Energy Definition of Work Calculation of Work Work of Linear Spring Work and Curvilinear Motion Principle of Work and Kinetic Energy Advantage of Work-Energy Method Power Examples 2. Potential Energy Gravitational Elastic PE PE Examples Examples 2103-212 Dynamics, NAV, 2012 3 3-2. Work and Energy 1. Introduction Recall Newton’s second law and notice that this is an instantaneous relationship. When we want to see changes in velocity or position due to motion, we have to integrate Newton’s second law by using appropriate kinematic equations. However, we may integrate Newton’s second law directly and avoid solving for acceleration first. In general, there is two classes of problems Integration with respect to displacement → Work-Energy equation → velocity between two positions of a particle or system’s configurations. Integration with respect to time → Impulse-Momentum equation → changes in velocity between two points in time. 2103-212 Dynamics, NAV, 2012 4 3-2. Work and Energy 2. Definition of Work 2103-212 Dynamics, NAV, 2012 5 3-2. Work and Energy 3. Calculation of Work 2103-212 Dynamics, NAV, 2012 6 3-2. Work and Energy 3. Calculation of Work Notes: 2103-212 Dynamics, NAV, 2012 7 3-2. Work and Energy 3. Calculation of Work Example 1: Collar and Guide Find the work done by the 8 N force on the collar when it moves from point A to point B. 2103-212 Dynamics, NAV, 2012 8 3-2. Work and Energy 3. Calculation of Work Example 2: Collar and Guide Find the work done by the force F on the collar when it moves from point A to any point. 2103-212 Dynamics, NAV, 2012 9 3-2. Work and Energy 3. Calculation of Work Example 2: continued 2103-212 Dynamics, NAV, 2012 10 3-2. Work and Energy 5. Work and Curvilinear Motion 2103-212 Dynamics, NAV, 2012 11 3-2. Work and Energy 6. Work and Kinetic Energy 2103-212 Dynamics, NAV, 2012 12 3-2. Work and Energy 6. Work and Kinetic Energy 2103-212 Dynamics, NAV, 2012 13 3-2. Work and Energy 6. Work and Kinetic Energy Example 3: Collar and Guide again 2103-212 Dynamics, NAV, 2012 14 3-2. Work and Energy 7. Power 2103-212 Dynamics, NAV, 2012 15 3-2. Work and Energy Example 4: Slider Ans: 4.48 m/s 2103-212 Dynamics, NAV, 2012 16 3-2. Work and Energy Example 5: Swinging Ball Ans: 3.59 m/s 2103-212 Dynamics, NAV, 2012 17 3-2. Work and Energy 8. Potential Energy Gravitational PE Elastic PE 8.1 Gravitational PE (Vg) Reference 2103-212 Dynamics, NAV, 2012 18 3-2. Work and Energy 8.1 Gravitational PE (Vg) Start low finish high = go up ΔVg = + Start high finish low = go down ΔVg = - 2103-212 Dynamics, NAV, 2012 19 3-2. Work and Energy 8.2 Elastic PE (Ve) x is how much the spring is compressed or extended from its relaxed (original length) 2103-212 Dynamics, NAV, 2012 20 3-2. Work and Energy 9. Alternate form of Work-KE equation 2103-212 Dynamics, NAV, 2012 21 3-2. Work and Energy 9. Alternate form of Work-KE equation 2103-212 Dynamics, NAV, 2012 22 3-2. Work and Energy 9. Alternate form of Work-KE equation Special Case (when there is no work from the external force other than mg and spring) Law of Conservation of Mechanical Energy 2103-212 Dynamics, NAV, 2012 23 3-2. Work and Energy Example 6: Spring and Slider Ans: 1.16 m/s 2103-212 Dynamics, NAV, 2012 24 3-2. Work and Energy Example 7: Spring and Slider Ans: 3.59 m/s 2103-212 Dynamics, NAV, 2012 25 3-2. Work and Energy Example 8: Slider The spring of stiffness k is compressed and released, sending the particle of mass m sliding along the track. Determine the minimum spring compression for which the particle will not lose contact with the track. The sliding surface is smooth except shown. 2103-212 Dynamics, NAV, 2012 26

































![Jet InsideNAV Instructions[1]](http://s1.studyres.com/store/data/003882343_1-30c57e443344fd4843436dcbdd81ba0f-150x150.png)