Download Document

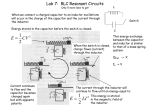
Electrical Oscillator
Prepared by;
Dr. Rajesh Sharma
Assistant Professor
Dept of Physics
P.G.G.C-11, Chandigarh
Email: [email protected]
Electrical Oscillator
• A circuit consisting of an inductance (L) and capacitance (C) serves as an
electrical oscillator which resembles a “mass-spring” oscillator, where
the role of mass is being played by the charge q on the capacitor.
•
•
•
•
•
•
•
•
Suppose, a capacitor containing a charge q0 on its plates is connected with an
inductor. The capacitor starts discharging through the inductor. (Fig.i)
The flow of charge constitutes a current and a magnetic field is setup in the
inductor coil L. Fig.ii shows the state of the oscillator when the capacitor is
completely discharges and maximum magnetic field is built up in the inductor
coil.
The variation of the magnetic field linked with the coil sets up a induced emf
across it, which in accordance with Lenz’s law is opposite to the potential
difference across the capacitor.
The emf , in turn charges the capacitor in the opposite direction (Fig.iii).
Again, charge q0 is collected on the plates of the capacitor, but the sign of
charge is opposite to that it was to start with. (Fig.i)
Now, the process of discharging of capacitor begins but the direction of the
current is opposite to that of the earlier case.
Again a magnetic field is setup across the inductor, but the direction of the
magnetic field is opposite to that set up in Fig.ii. The variation of magnetic flux
again sets up induced emf which charges the capacitor obtaining the original
state (Fig.i).
One oscillation is completed and the system is again ready for next oscillation.
Differential Equation for the Electrical Oscillator
• The induced e.m.f. in the inductor, according to faraday’s law is given by
dI
L  L
dt
where I is the current in the circuit.
dq
I
since,
dt
d 2q
L  L 2

dt
q
The potential drop across the capacitor is  C 
, where q is the
C
instantaneous charge on the plates for the capacitor.
Applying Kirchoff’s second law, we get
 L  C
2
d
q q
Or,
L 2 
dt
C
• Which can be written as,
d 2q q
L 2  0
dt
C
2
d
q q
Or,
(1)

0
2
dt
LC
This is the differential equation for the electrical oscillator.
• Comparing it with the differential equation for the mechanical oscillator, it
is found that the displacement ‘x’ of the mechanical oscillator is
represented by the charge ‘q’ , which is the variable physical quantity for
the electrical oscillator.
1
1
2
f

• Here 0 
and hence the frequency of oscillations is given
2 LC
LC
• The eq. of the SHM which is also the solution of the Differential equation
(2)
q  q0 cos 0t
• Where q0 is the amplitude, i.e. the maximum value of the charge on the
plates of capacitor
Energy of the capacitor
• If the charge on the plates of the capacitor is q , then the potential energy
across the plates is q/C.
• Therefore, if we wish to add a small charge dq to the plates, then work
done, which is equal to the electric energy stored is given by
q
dU C  dq
C
• Therefore, total energy stored on the capacitor, when charge on the plates
is q , is given by
q
U C   dU C   dq
C
• Or,
1 q2
UC 
2C
(2)
Energy of the Inductor
dI
• The induced emf on the inductor is  L  L
. So, when the current in the
dt
inductor is I , the energy stored is:
dI
Idt  LIdI
dt
• So, the total energy on the inductor is:
1 2
U L   dU L   LIdI  LI
2
dU L   L Idt  L
• But,
dq
I
dt
therefore
1  dq 
U L  L 
2  dt 
2
(4)
Total Energy
• The total energy of the electrical oscillator or the total EM energy is given
by:
U EM  U L  U C
2
Or,
U EM
1  dq  1 q 2
 L  
2  dt  2 C
(5)
q  q0 cos 0t we get
1
1 q02
2
U EM  L q00 sin 0t  
cos 2 0t
2
22 C
• Or,
1 2 2 2
1 q0
U EM  Lq0 0 sin 0t 
cos 2 0t
2
1
1 2C
2
2
• But, 0 
. Therefore, L0  . Hence, substituting the value of
C
1/C, we get LC
1 2 2 2
1 2 2
U EM  Lq0 0 sin 0t  q0 L0 cos 2 0t
2
2
1 2 2
U EM  Lq0 0 sin 2 0t  cos 2 0t 
Or,
2
1 2 2
Or,
(6)
U EM  Lq0 0
2
substituting
This again shows that the total energy of the oscillator is conserved and depends upon L, q0 and w0 as well as C