* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Particle in a box wikipedia , lookup
EPR paradox wikipedia , lookup
Renormalization wikipedia , lookup
History of quantum field theory wikipedia , lookup
Ferromagnetism wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Double-slit experiment wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Chemical bond wikipedia , lookup
Matter wave wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Molecular orbital wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Tight binding wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Atomic theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
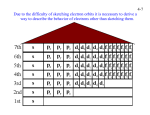
Chapter 5 Periodicity and the Electronic Structure of Atoms 國防醫學院 生化學科 王明芳老師 2011-10-4 1 2 Light and the Electromagnetic Spectrum Electromagnetic energy (―light‖) is characterized by wavelength, frequency, and amplitude. Chapter 5/3 Light and the Electromagnetic Spectrum Chapter 5/4 Light and the Electromagnetic Spectrum l Chapter 5/5 Light and the Electromagnetic Spectrum Wavelength x Frequency = Speed l m x 1 s = c m s hertz (Hz; 1 Hz = 1s-1) c is defined to be the rate of travel of all electromagnetic energy in a vacuum and is a constant value—speed of m light. 8 c = 3.00 x 10 s Chapter 5/6 Light and the Electromagnetic Spectrum The light blue glow given off by mercury streetlamps has a frequency of 6.88 x 1014 s-1 (or, Hz). What is the wavelength in nanometers? l= c = m 8 3.00 x 10 s 6.88 x 1 x 109 nm m 1014 1 s = 436 nm Chapter 5/7 Example 5.1 Calculating A Frequency From A Wavelength The light blue glow given off by mercury streetlamps has a wavelength of 436 nm. What is its frequency in hertz? Solution Don’t forget to convert from nanometers to meters. Electromagnetic Energy and Atomic Line Spectra Glass prism sundog Chapter 5/9 Electromagnetic Energy and Atomic Line Spectra Line Spectrum: A series of discrete lines on an otherwise dark background as a result of light emitted by an excited atom Atomic line spectra Chapter 5/10 Electromagnetic Energy and Atomic Line Spectra Johann Balmer in 1885 discovered a mathematical relationship for the four visible lines in the atomic line spectra for hydrogen. 1 1 1 m = 2 visible light =R 22 n2 l Johannes Rydberg later modified the equation to fit every line in the entire spectrum of hydrogen. 1 1 1 =R m2 n2 l m=1 m=3 UV light infrared light R (Rydberg Constant) = 1.097 x 10-2 nm-1 Chapter 5/11 Example 5.2 Using The Balmer–Rydberg Equation What are the two longest-wavelength lines in nanometers in the series of the hydrogen spectrum when m = 1 and n > 1? Solution The wavelength l is greatest when n is smallest; that is, when n = 2 and n = 3. Solving the equation first for n = 2 gives Example 5.2 Using The Balmer–Rydberg Equation Continued The two longest-wavelength lines are at 121.5 nm and 102.6 nm. Example 5.3 Using The Balmer–Rydberg Equation What is the shortest-wavelength line in nanometers in the series of the hydrogen spectrum when m = 1 and n > 1? Solution The shortest-wavelength line occurs when is infinitely large so that 1/n2 is zero. That is, if n = , then 1/n2 = 0. Solution The shortest-wavelength line is at 91.16 nm. Particlelike Properties of Electromagnetic Energy Photoelectric Effect: Irradiation of clean metal surface with light causes electrons to be ejected from the metal. Furthermore, the frequency of the light used for the irradiation must be above some threshold value, which is different for every metal. A glass window can be broken by a single baseball, but a thousand Ping-Pong ball would only bounce off. Chapter 5/15 Particlelike Properties of Electromagnetic Energy The photoelectric effect: the energy of an individual photo depends only on its frequency (or wavelength), not on the intensity of the light beam. The intensity of a light beam is a measure of the number of photo in the beam. Chapter 5/16 Particlelike Properties of Electromagnetic Energy E = h E h (Planck’s constant) = 6.626 x 10-34 J s Electromagnetic energy (light) is quantized. Chapter 5/17 Particlelike Properties of Electromagnetic Energy Niels Bohr proposed in 1914 a model of the hydrogen atom as a nucleus with an electron circling around it. In this model, the energy levels of the orbits are quantized so that only certain specific orbits corresponding to certain specific energies for the electron are available. Chapter 5/18 Particlelike Properties of Electromagnetic Energy Chapter 5/19 Example 5.4 Calculating the Energy of a Photon from its Frequency What is the energy in kilojoules per mole of radar waves with = 3.35 108 Hz? Strategy 1. E = h 2. To find the energy per mole of photons, the energy of one photon must be multiplied by Avogadro’s number. Solution Wavelike Properties of Matter Louis de Broglie in 1924 suggested that, if light can behave in some respects like matter, then perhaps matter can behave in some respects like light. In other words, perhaps matter is wavelike as well as particlelike. h l= mv The de Broglie equation allows the calculation of a ―wavelength‖ of an electron or of any particle or object of mass m and velocity v. Chapter 5/21 Wavelike Properties of Matter What is the de Broglie wavelength in meters of a small car with a mass of 1150 kg traveling at a velocity of 24.6 m/s? l= h = mv 2 kg m 6.626 x 10-34 s m (1150 kg) 24.6 s = 2.34 x 10-38 m Chapter 5/22 Quantum Mechanics and the Heisenberg Uncertainty Principle In 1926 Erwin Schrödinger proposed the quantum mechanical model of the atom which focuses on the wavelike properties of the electron. In 1927 Werner Heisenberg stated that it is impossible to know precisely where an electron is and what path it follows—a statement called the Heisenberg uncertainty principle. Chapter 5/23 Wave Functions and Quantum Numbers Wave solve Wave function equation or orbital (Y ) Probability of finding electron in a region of space (Y 2) A wave function is characterized by three parameters called quantum numbers, n, l, ml. Chapter 5/24 Wave Functions and Quantum Numbers Principal Quantum Number (n) • Describes the size and energy level of the orbital • Commonly called a shell • Positive integer (n = 1, 2, 3, 4, …) • As the value of n increases: • The energy increases • The average distance of the e- from the nucleus increases Chapter 5/25 Wave Functions and Quantum Numbers Angular-Momentum Quantum Number (l) • Defines the three-dimensional shape of the orbital • Commonly called a subshell • There are n different shapes for orbitals • If n = 1 then l = 0 • If n = 2 then l = 0 or 1 • If n = 3 then l = 0, 1, or 2 • Commonly referred to by letter (subshell notation) • l=0 s (sharp) • l=1 p (principal) • l=2 d (diffuse) • l=3 f (fundamental) Chapter 5/26 Wave Functions and Quantum Numbers Magnetic Quantum Number (ml ) • Defines the spatial orientation of the orbital • There are 2l + 1 values of ml and they can have any integral value from -l to +l • If l = 0 then ml = 0 • If l = 1 then ml = -1, 0, or 1 • If l = 2 then ml = -2, -1, 0, 1, or 2 • etc. Chapter 5/27 Wave Functions and Quantum Numbers Chapter 5/28 Wave Functions and Quantum Numbers Chapter 5/29 Wave Functions and Quantum Numbers Identify the possible values for each of the three quantum numbers for a 4p orbital. Chapter 5/30 Wave Functions and Quantum Numbers Identify the possible values for each of the three quantum numbers for a 4p orbital. n=4 l=1 ml = -1, 0, or 1 Chapter 5/31 Example 5.5 Using Quantum Numbers To Identify An Orbital Identify the shell and subshell of an orbital with the quantum numbers n = 3, l = 1, ml = 1. Solution 1. The principal quantum number gives the shell number 2. The angular-momentum quantum number gives the subshell designation. 3. The magnetic quantum number ml is related to the spatial orientation of the orbital. A value of n = 3 indicates that the orbital is in the third shell, and a value of l = 1 indicates that the orbital is of the p type. Thus, the orbital has the designation 3p. Example 5.6 Assigning Quantum Numbers To An Orbital Give the possible combinations of quantum numbers for a 4p orbital. Solution The designation 4p indicates that the orbital has a principal quantum number n = 4 and an angular-momentum quantum number l = 1. The magnetic quantum number ml can have any of the three values 1, 0, or +1. The allowable combinations are n = 4, l = 1, ml = 1 n = 4, l = 1, ml = 0 n = 4, l = 1, ml = +1 The Shapes of Orbitals Node: A surface of zero probability for finding the electron Representations of 1s, 2s, and 3s orbitals Chapter 5/34 The Shapes of Orbitals s Orbital Shapes: 1. All s orbitals are spherical; The probability of finding an s electron depends only on distance from the nucleus, not on direction. 2. Only one orientation of a sphere in space, ml = 0 3. Only one s orbital per shell. 4. The size of the s orbital is successively higher shells an electron in an outer-shell s orbital is farther from the nucleus on average than and electron in an inner-shell s orbital. Chapter 5/35 The Shapes of Orbitals Node: A surface of zero probability for finding the electron Chapter 5/36 The Shapes of Orbitals Representations of the three 2p orbitals Chapter 5/37 The Shapes of Orbitals p Orbital Shapes: 1. The p orbitals are dumbbell-shaped, with their electron distribution concentrated in identical lobes on either side of the nucleus and separated by a nodal plane passing through the nucleus. 2. These two lobes have different phases. Only lobes of the same phase can interact in forming covalent chemical bonds. Chapter 5/38 Representations of the five 3d orbitals (a-d) Also shown is one of the seven 4f orbital (f) The Shapes of Orbitals d and f Orbital Shapes: 1. Four d orbitals are cloverleaf-shaped, with four lobes separated by two nodal planes through the nucleus; one is similar in shape to a pz but with a donut-shaped region of electron probability. 2. Both the number of nodal planes and the geometric complexity of the orbitals increases with the quantum number increases of the subshell. Chapter 5/40 Quantum Mechanics and Atomic Line Spectra The origin of atomic line spectra. The energies available to electrons are quantized and can have only the specific values associated with the orbitals they occupy. Chapter 5/41 Quantum Mechanics and Atomic Line Spectra m: shell the transition is to (inner-shell) 1 1 1 =R 2 m n2 l n: shell the transition is from (outer-shell) Chapter 5/42 Example 5.7 Calculating The Energy Difference Between Two Orbitals What is the energy difference in kilojoules per mole between the first and second shells of the hydrogen atom if the lowest-energy emission in the spectral series with m = 1 and n = 2 occurs at l = 121.5 nm? Solution 1. The lowest-energy emission line in the spectral series with m = 1 and n = 2 corresponds to the emission of light as an electron falls from the second shell to the first shell 2. The energy of that light equal to the energy difference between shells. 3. Knowing the wavelength of the light, we can calculate the energy of one photon using the equation, E = hc/l , and then multiply by Avogadro’s number to find the answer in joules (or kilojoules) per mole: The energy difference between the first and second shells of the hydrogen atom is 985 kJ/mol. Electron Spin and the Pauli Exclusion Principle Electrons have spin which gives rise to a tiny magnetic field and to a spin quantum number (ms). Spin quantum number (ms) can have either of two values, +1/2 or -1/2. The value of ms is independent of the other three quantum number, unlike the values of n, l, and ml, which are interrelated Electron spin Pauli Exclusion Principle: No two electrons in an atom can have the same four quantum numbers. Chapter 5/44 Orbital Energy Levels in Multielectron Atoms Effective Nuclear Charge (Zeff): The nuclear charge actually felt by an electron Zeff = Zactual - Electron shielding Effective Nuclear Charge, Zeff 1. The energy split between subshells is comes from the balance of attractions and repulsions in the atom. 2. Shielding effect: Each electrons is shielded from the full attraction of the nucleus by the other electrons in the atom. 3. Electron shielding leads to energy differences among orbitals within a shell. Chapter 5/46 Effective Nuclear Charge, Zeff 4. Net nuclear charge felt by an electron is called the effective nuclear charge (Zeff). 5. Zeff is lower than actual nuclear charge. 6. Electrons in different orbitals are shielded differently and feel different values of Zeff. 7. This explains certain periodic changes observed. Chapter 5/47 Orbital Energy Levels in Multielectron Atoms Effective Nuclear Charge (Zeff): The nuclear charge actually felt by an electron Zeff = Zactual - Electron shielding Chapter 5/48 Electron Configurations of Multielectron Atoms Electron Configuration: A description of which orbitals are occupied by electrons Degenerate Orbitals: Orbitals that have the same energy level. For example, the three p orbitals in a given subshell Ground-State Electron Configuration: The lowest-energy configuration Aufbau Principle (“building up”): A guide for determining the filling order of orbitals Chapter 5/49 Electron Configurations of Multielectron Atoms Rules of the aufbau principle: 1. Lower-energy orbitals fill before higher-energy orbitals. 2. An orbital can only hold two electrons, which must have opposite spins (Pauli exclusion principle). 3. If two or more degenerate orbitals are available, follow Hund’s rule. Hund’s Rule: If two or more orbitals with the same energy are available, one electron goes into each until all are halffull. The electrons in the half-filled orbitals all have the same value of their spin quantum number. Chapter 5/50 Electron Configurations of Multielectron Atoms Chapter 5/51 Electron Configuration of Multielectron Atoms Increasing Energy Core [He] [Ne] [Ar] [Kr] [Xe] [Rn] 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 7p 3d 4d 4f 5d 5f 6d Chapter 5/52 Electron Configurations of Multielectron Atoms Electron Configuration H: 1s1 1 electron s orbital (l = 0) n=1 Chapter 5/53 Electron Configurations of Multielectron Atoms Electron Configuration H: 1s1 He: 1s2 2 electrons s orbital (l = 0) n=1 Chapter 5/54 Electron Configurations of Multielectron Atoms Electron Configuration H: He: Li: 1s1 1s2 Lowest energy to highest energy 1s2 2s1 1 electron s orbital (l = 0) n=2 Chapter 5/55 Electron Configurations of Multielectron Atoms Electron Configuration H: 1s1 He: 1s2 Li: 1s2 2s1 N: 1s2 2s2 2p3 3 electrons p orbital (l = 1) n=2 Chapter 5/56 Electron Configurations of Multielectron Atoms Electron Configuration H: Orbital-Filling Diagram 1s1 1s He: 1s2 Li: 1s2 2s1 N: 1s2 2s2 2p3 Chapter 5/57 Electron Configurations of Multielectron Atoms Electron Configuration H: Orbital-Filling Diagram 1s1 1s He: 1s2 Li: 1s2 2s1 N: 1s2 2s2 2p3 1s Chapter 5/58 Electron Configurations of Multielectron Atoms Electron Configuration H: Orbital-Filling Diagram 1s1 1s He: 1s2 Li: 1s2 2s1 N: 1s2 2s2 2p3 1s 1s 2s Chapter 5/59 Electron Configurations of Multielectron Atoms Electron Configuration H: Orbital-Filling Diagram 1s1 1s He: 1s2 Li: 1s2 2s1 N: 1s2 2s2 2p3 1s 1s 2s 1s 2s 2p Chapter 5/60 Electron Configurations of Multielectron Atoms Electron Configuration Na: P: 1s2 2s2 2p6 3s1 Shorthand Configuration [Ne] 3s1 1s2 2s2 2p6 3s2 3p3 Ne configuration Chapter 5/61 Electron Configurations of Multielectron Atoms Electron Configuration Na: Shorthand Configuration 1s2 2s2 2p6 3s1 Ne configuration Chapter 5/62 Electron Configurations of Multielectron Atoms Electron Configuration Na: 1s2 2s2 2p6 3s1 Shorthand Configuration [Ne] 3s1 Ne configuration Chapter 5/63 Electron Configurations of Multielectron Atoms Electron Configuration Na: P: Shorthand Configuration 1s2 2s2 2p6 3s1 [Ne] 3s1 1s2 2s2 2p6 3s2 3p3 [Ne] 3s2 3p3 Ne configuration Chapter 5/64 Electron Configurations of Multielectron Atoms Electron Configuration Shorthand Configuration 1s2 2s2 2p6 3s1 [Ne] 3s1 P: 1s2 2s2 2p6 3s2 3p3 [Ne] 3s2 3p3 K: 1s2 2s2 2p6 3s2 3p6 4s1 [Ar] 4s1 1s2 2s2 2p6 3s2 3p6 4s2 3d1 [Ar] 4s2 3d1 Na: Sc: Ar configuration Chapter 5/65 Electron Configurations of Multielectron Atoms Electron Configuration Shorthand Configuration 1s2 2s2 2p6 3s1 [Ne] 3s1 P: 1s2 2s2 2p6 3s2 3p3 [Ne] 3s2 3p3 K: 1s2 2s2 2p6 3s2 3p6 4s1 Na: Ar configuration Chapter 5/66 Electron Configurations of Multielectron Atoms Electron Configuration Shorthand Configuration 1s2 2s2 2p6 3s1 [Ne] 3s1 P: 1s2 2s2 2p6 3s2 3p3 [Ne] 3s2 3p3 K: 1s2 2s2 2p6 3s2 3p6 4s1 [Ar] 4s1 Na: Ar configuration Chapter 5/67 Electron Configurations of Multielectron Atoms Electron Configuration Shorthand Configuration 1s2 2s2 2p6 3s1 [Ne] 3s1 P: 1s2 2s2 2p6 3s2 3p3 [Ne] 3s2 3p3 K: 1s2 2s2 2p6 3s2 3p6 4s1 [Ar] 4s1 Na: Sc: 1s2 2s2 2p6 3s2 3p6 4s2 3d1 [Ar] 4s2 3d1 Ar configuration Chapter 5/68 Some Anomalous Electron Configurations Expected Configuration Actual Configuration Cr: [Ar] 4s2 3d4 [Ar] 4s1 3d5 Cu: [Ar] 4s2 3d9 [Ar] 4s1 3d10 Chapter 5/69 Outer-shell, ground-stead electron configuration of the elements Electron Configurations and the Periodic Table Blocks of the periodic table Electron Configuration of Multielectron Atoms Increasing Energy Core [He] [Ne] [Ar] [Kr] [Xe] [Rn] 1s 2s 3s 4s 5s 6s 7s 2p 3p 4p 5p 6p 7p 3d 4d 4f 5d 5f 6d Chapter 5/72 Electron Configurations and the Periodic Table Valence Shell: Outermost shell. Li: 2s1 Na: 3s1 Cl: 3s2 3p5 Br: 4s2 4p5 Chapter 5/73 Example 5.8 Assigning A Ground-State Electron Configuration To An Atom Give the ground-state electron configuration of arsenic, Z = 33, and draw an orbital-filling diagram, indicating the electrons as up or down arrows. Solution 1. 2. 3. Start with hydrogen at the upper left Fill orbitals until 33 electrons have been added. Remember that only 2 electrons can go into an orbital and that each one of a set of degenerate orbitals must be half filled before any one can be completely filled. As: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p3 or [Ar] 4s2 3d10 4p3 An orbital-filling diagram indicates the electrons in each orbital as arrows. Note that the three 4p electrons all have the same spin: Example 5.9 Identifying An Atom From Its Ground-State Electron Configuration Identify the atom with the following ground-state electron configuration: Solution 1. 2. One way to do this problem is to identify the electron configuration and decide which atom has that configuration. Alternatively, you can just count the electrons, thereby finding the atomic number of the atom. The atom whose ground-state electron configuration is depicted is in the fifth row because it follows krypton. It has the configuration 5s2 4d5, which identifies it as technetium. Alternatively, it has 36 + 7 = 43 electrons and is the element with Z = 43. Electron Configurations and Periodic Properties: Atomic Radii column radius row radius Atomic radii of the elements in picometers Chapter 5/76 Electron Configurations and Periodic Properties: Atomic Radii Plots of atomic radius and calculated Zeff for the highestenergy electron versus atomic number Chapter 5/77