* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download L12_Alternating_Current
Josephson voltage standard wikipedia , lookup
Schmitt trigger wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Regenerative circuit wikipedia , lookup
Operational amplifier wikipedia , lookup
Radio transmitter design wikipedia , lookup
Electrical ballast wikipedia , lookup
Surge protector wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Index of electronics articles wikipedia , lookup
Power electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Power MOSFET wikipedia , lookup
Current source wikipedia , lookup
Current mirror wikipedia , lookup
Opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
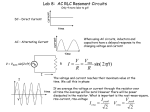
Alternating Current Kirchoff’s rules for loops and junctions may be used to analyze complicated circuits such as the one below, powered by an alternating current (A.C.) source. But the analysis can quickly become much more complicated. In this chapter we consider the behavior of basic, but useful, circuits driven by A.C. sources. Symbol for A.C. source. A.C. Demo Simple alternating current (A.C.) generator In a basic A.C. generator, a permanent magnet provides a reasonably uniform magnetic field. As the generator loop turns in this field at frequency w (rad/s), the flux through the loop changes sinusoidally with time. This causes the output voltage (induced emf) to also change sinusoidally, 90 degrees out of phase with the flux. We can see why this happens by applying Faraday’s Law of Induction to the flux: Let: B 0 cos(wt ) Then: d [ 0 cos(wt )] dt w 0 sin( wt ) emf VMAX sin( wt ) Motional emf Resistor connected to A.C. source VMAX sin( wt ) V RI VMAX sin( wt ) VR RI R VR VMAX sin( wt ) I MAX sin( wt ) So the current in the resistor is: I R R R Use Kirchoff’s loop equation: Note that the resistor voltage and current are in phase. (See plot.) 2 P RI R2 RI MAX sin 2 (wt ) Instantaneous power dissipation: To find the average power (root mean square, “RMS”), integrate over one cycle: PRMS 2 / w 0 So that: I 2 RMS 2 I MAX RI 2 2 MAX 1 2 2 sin( wt )dt RI MAX RI RMS 2 I MAX 2 .707 I MAX I RMS Inductor connected to A.C. source VMAX sin( wt ) VL L dI L dt Use Kirchoff’s loop equation: L dI L VMAX sin( wt ) dt Integrate to solve for IL: I L VMAX VMAX VMAX sin( w t ) dt cos( w t ) sin( w t ) L wL wL 2 From either the equations or the graph we see that, for A.C. sources, the current in an inductor lags behind its voltage by 90o Inductive Reactance, XL Notice that whenever cos(wt) is +1 or -1, the magnitude of the current in the inductor is at the maximum. We can express this as follows: I MAX IL VMAX cos(wt ) wL VMAX wL This equation has the same structure as Ohm’s Law, and we can identify the factor in the denominator as setting the ratio between V and I. We call this factor the inductive reactance, and define it as follows: X L wL And since RMS voltage and current are one-half their values at maximum, XL can be used in both equations: VMAX X L I MAX VRMS X L I RMS •It’s clear from these equations that XL must have units of ohms. •Unlike resistance, inductive reactance changes with frequency! Example Capacitor connected to A.C. source VMAX sin( wt ) VC Q C Q VMAX sin( wt ) Q CVMAX sin( wt ) C dQ Differentiate to find IC: I C wCVMAX cos(wt ) wCVMAX sin( wt ) dt 2 Kirchoff’s loop equation: From either the equations or the graph we see that, for A.C. sources, the current in a capacitor leads its voltage by 90o Capacitive Reactance, XC Again, whenever cos(wt) is +1 or -1, the magnitude of the current in the capacitor is at the maximum. We can express this as follows: I C wCVMAX cos(wt ) I MAX wCVMAX This equation has the same structure as Ohm’s Law, and we can identify the factor multiplying V as setting the ratio between V and I. We define the capacitive reactance as the inverse of this factor: 1 XC wC And since RMS voltage and current are one-half their values at maximum, XC can be used in both equations: VMAX X C I MAX VRMS X C I RMS •As with XL , XC must have units of ohms. •And as before, this capacitive reactance changes with frequency! Example Frequency dependence of R, XL, and XC X L wL V RI XC 1 wC The Driven RLC Circuit We have already studied the damped oscillations of an RLC circuit which has been energized with an initial charge or current. But now we consider the response of this circuit when it is driven by an AC source, which feeds energy into the circuit. We will see how this reaches an equilibrium, with the power from the source being dissipated by the resistor. Analyzing the Driven RLC Circuit Since this circuit consists of one loop, the same current, I, passes through every element in the circuit. Once again, we can use Kirchoff’s loop equation for voltages. Using V for the source voltage: V VL VC VR Now we insert all the equations from previous pages. With this more complicated circuit the phase of the source will no longer be the same as that for the resistor. So we let the source voltage be displaced by –f. VMAX sin( wt ) RI MAX sin( wt ) X L I MAX cos(wt ) X C I MAX cos(wt ) For t = 0: For wt = /2: VMAX sin( ) X L I MAX X C I MAX ( X L X C ) I MAX VMAX sin( / 2 ) VMAX cos( ) RI MAX Square and add: 2 2 VMAX I MAX R 2 ( X L X C )2 Define “impedance”, Z: Z R 2 ( X L X C ) 2 VMAX ZI MAX We can think of “impedance”, Z, as “total resistance at a given frequency w. Measuring voltages in an RLC Circuit. Voltages as a function of time in a typical RLC Circuit. Frequency dependence of reactances and impedance in RLC Circuit At the frequency where XL= XC , the impedance of the circuit is at a minimum, and Z = R. Since Z is minimum at the point where XL= XC the average current is maximum. The power dissipation is also maximum at this point, meaning that the power delivered to the circuit by the AC source is maximum. At what frequency does this occur? X L X C wL 1 1 w2 w wC LC 1 LC But this is the frequency of an LC circuit when there is no resistor present! At this frequency, the circuit is in resonance, with the driving frequency, w, equal to the natural frequency of the LC oscillator, wo. Current as a function of w in a driven RLC circuit w0 1 LC The plot at right shows current resonance curves for several values of R. The greater the resistance, the lower the maximum current. We can calculate the shapes of these resonance curves as follows: I RMS VRMS Z VRMS R 2 ( X L X C )2 VRMS L2 1 2 R 2 (w ) w LC 2 2 VRMS R 2 L2 w 2 (w 2 wo2 ) 2 Resonance curves for a damped, driven harmonic oscillator: mass + spring + damping. Collapse of Tacoma Narrows bridge in 1940 driven into resonance by wind. Too little damping! Coils sharing the same magnetic flux, BA These can be used as “transformers”. In air With iron yoke Raising and Lowering A.C. Voltage: Transformers Faraday’s Law of Induction tells us the relationship between the magnitudes of the voltage at the terminals and the rate of change of magnetic flux through each coil: d 2 d 1 V2 N 2 dt dt But the flux through each coil is the same: V1 N1 1 2 d1 d 2 dt dt V1 V2 N1 N 2 So the output (secondary) voltage can be raised or lowered compared to the input (primary) voltage, by the ratio of turns. A transformer that raises (lowers) voltage is called a “step-up” (“step-down”) transformer. Transformers lose very little power: P V1I1 V2 I 2 N2 V2 V1 N1 V1 N1 I 2 I1 I1 V2 N2 As the voltage is increased, the current is lowered by the same factor. Transformers are not perfect, but they dissipate little power. Nikola Tesla (Serbian Cyrillic: Никола Тесла; 10 July 1856 – 7 January 1943) was a Serbian-American inventor, mechanical engineer, and electrical engineer. He was an important contributor to the birth of commercial electricity, and is best known for his many revolutionary developments in the field of electromagnetism in the late 19th and early 20th centuries building on the theories of electromagnetic technology discovered by Michael Faraday and used in direct current (DC) applications. Tesla's patents and theoretical work formed the basis of modern alternating current (AC) electric power systems, including the polyphase system of electrical distribution and the AC motor. Tesla Coil Schematic Tesla Never Thought Small Tesla’s A.C. Dynamo (generator) used to generate alternating currrent electricity, which became the technology of choice for electrification across the U.S. (power grids) and ultimately, the whole planet. U.S. Patent 390721 Wardenclyffe Tower facility ~ 1915 Mark Twain in Tesla’s Lab. A.C. power networks Transmission lines: 155,000-765,000 V Local substation: 7,200 V House: 110/220 V For a given length of power line, P=RI2. If the power line voltage is 550,000 V, the current is reduced by a factor of 5000 compared to that at 110 V, and the power loss is reduced by a factor of 25 million.