Download 8-4 Similarity in Right Triangles M11.C.1 2.2.11.A

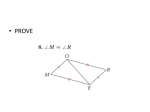
8-4 Similarity in Right Triangles
M11.C.1 2.2.11.A
OBJECTIVES:
1) TO FIND AND USE RELATIONSHIPS IN SIMILAR
RIGHT TRIANGLES.
THEOREM
 The altitude to the hypotenuse of a right triangle
divides the triangle into two triangles that are similar
to the original triangle and to each other.
Vocabulary
 For any two positive numbers a and b, the geometric
mean of a and b is the positive number x such that:
𝑎
𝑥
=
𝑥
𝑏
**Example: Find the geometric mean of 3 and 12
Example
 Find the geometric mean of 4 and 18.
Corollary to Theorem
 The length of the altitude to the hypotenuse of a right
triangle is the geometric mean of the lengths of the
segments of the hypotenuse
Corollary to Theorem
 The altitude to the hypotenuse of a right triangle
separates the hypotenuse so that the length of each
leg of the triangle is the geometric mean of the length
of the adjacent hypotenuse segment and the length
of the hypotenuse.
Example: Apply Corollaries 1 and 2
Solve for x and y
Example
 Solve for x and y using the corollaries.