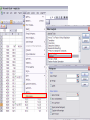
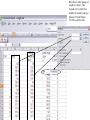
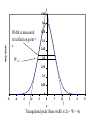
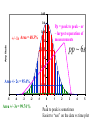
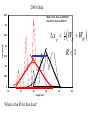
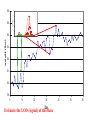
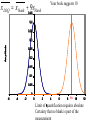
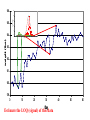
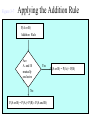
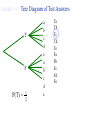
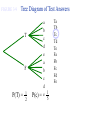
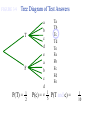
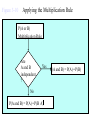
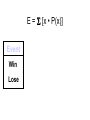
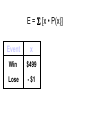
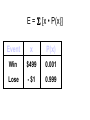
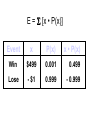
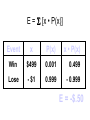
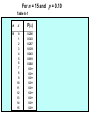
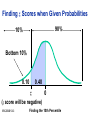
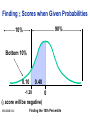
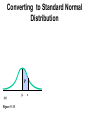
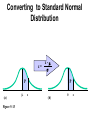
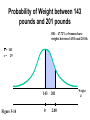
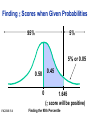
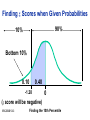
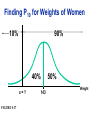
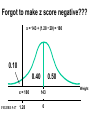
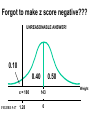
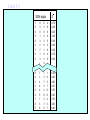
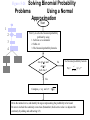
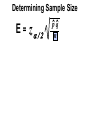
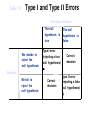
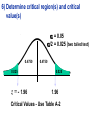
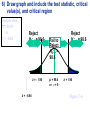
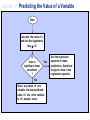
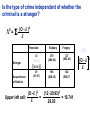
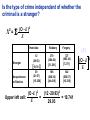
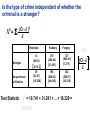
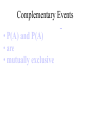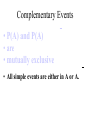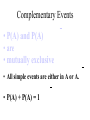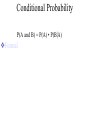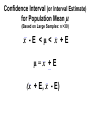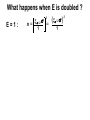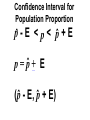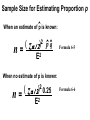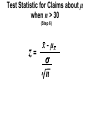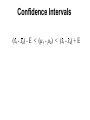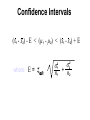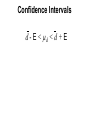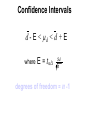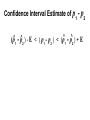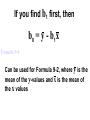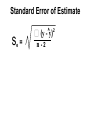* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Inductive probability wikipedia , lookup
Sufficient statistic wikipedia , lookup
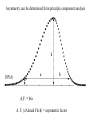
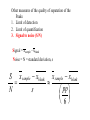
Degrees of freedom (statistics) wikipedia , lookup
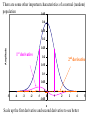
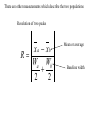
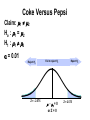
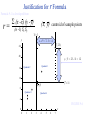
Confidence interval wikipedia , lookup
Foundations of statistics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
History of statistics wikipedia , lookup
Taylor's law wikipedia , lookup
German tank problem wikipedia , lookup
Resampling (statistics) wikipedia , lookup
ELEMENTARY STATISTICS Introduction to Geostatistics Dept of Energy & Mineral Resources Eng., Sejong University Myung Chae JUNG ELEMENTARY MARIO F. TRIOLA STATISTICS EIGHTH EDITION Handling Data and Figures of Merit Data come in different formats time Histograms Lists But…. Can contain the same information about quality What is meant by quality? (figures of merit) Precision, separation (selectivity), limits of detection, Linear range My weight day weight 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 140 140.1 139.8 140.6 140 139.8 139.6 140 140.8 139.7 140.2 141.7 141.9 141.4 142.3 142.3 141.9 142.1 142.5 142.3 142.1 142.5 143.5 143 143.2 143 143.4 143.5 142.7 143.7 day 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 weight day 143.9 144 142.5 142.9 142.8 143.9 144 144.8 143.9 144.5 143.9 144 144.2 143.8 143.5 143.8 143.2 143.5 143.6 143.4 143.9 143.6 144 143.8 143.6 143.8 144 144.2 144 143.9 weight 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 Plot as a function of time data was acquired: 144 144.2 144.5 144.2 143.9 144.2 144.5 144.3 144.2 144.9 144 143.8 144 143.8 144 144.5 143.7 143.9 144 144.2 144 144.4 143.8 144.1 day Comments: background is white (less ink); Font size is larger than Excel default (use 14 or 16) 146 145 144 weight (lbs) weight 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 140 140.1 139.8 140.6 140 139.8 139.6 140 140.8 139.7 140.2 141.7 141.9 141.4 142.3 142.3 141.9 142.1 142.5 142.3 142.1 142.5 143.5 143 143.2 143 143.4 143.5 142.7 143.7 day 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 weight day 143.9 144 142.5 142.9 142.8 143.9 144 144.8 143.9 144.5 143.9 144 144.2 143.8 143.5 143.8 143.2 143.5 143.6 143.4 143.9 143.6 144 143.8 143.6 143.8 144 144.2 144 143.9 143 142 Do not use curved lines to connect data points – that assumes you know more about the relationship of the data than you really do 141 140 139 0 10 20 30 Day 40 50 60 weight 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 144 144.2 144.5 144.2 143.9 144.2 144.5 144.3 144.2 144.9 144 143.8 144 143.8 144 144.5 143.7 143.9 144 144.2 144 144.4 143.8 144.1 Bin refers to what groups of weight to cluster. Like A grade curve which lists number of students who got between 95 and 100 pts 95-100 would be a bin Assume my weight is a single, random, set of similar data 25 Make a frequency chart (histogram) of the data 146 145 # of Observations 144 weight (lbs) 20 143 142 141 15 140 139 0 10 20 30 40 50 60 Day 10 5 0 Weight (lbs) Create a “model” of my weight and determine average Weight and how consistent my weight is 25 average 143.11 # of Observations 20 15 10 Inflection pt s = 1.4 lbs 5 0 Weight (lbs) s = standard deviation = measure of the consistency, or similarity, of weights Characteristics of the Model Population (Random, Normal) A f x e s 2 1 x m 2 s 2 Peak height, A Peak location (mean or average), m Peak width, W, at baseline Peak width at half height, W1/2 Standard deviation, s, estimates the variation in an infinite population, s Related concepts 0.45 0.4 0.35 Amplitude Width is measured At inflection point = s 0.3 0.25 0.2 W1/2 0.15 0.1 0.05 0 -5 -4 -3 -2 -1 0 1 2 3 4 s Triangulated peak: Base width is 2s < W < 4s 5 0.45 0.4 Pp = peak to peak – or – largest separation of measurements 0.35 +/- 1s Area = 68.3% Amplitude 0.3 pp ~ 6s 0.25 0.2 0.15 0.1 Area +/- 2s = 95.4% 0.05 0 -5 -4 -3 -2 Area +/- 3s = 99.74 % -1 0 1 2 3 4 5 s Peak to peak is sometimes Easier to “see” on the data vs time plot pp ~ 6s (Calculated s= 1.4) 146 144.9 145 Peak to peak 143 25 142 20 # of Observations weight (lbs) 144 141 15 10 5 140 139.5 0 Weight (lbs) 139 0 10 20 30 Day s~ pp/6 = (144.9-139.5)/6~0.9 40 50 60 There are some other important characteristics of a normal (random) population 0.45 0.4 0.35 0.3 Amplitude 0.25 1st derivative 0.2 2nd derivative 0.15 0.1 0.05 0 -5 -4 -3 -2 -1 -0.05 0 1 2 3 4 s Scale up the first derivative and second derivative to see better 5 Population, 0th derivative 0.6 0.4 Amplitude 0.2 0 -5 -4 -3 -2 -1 0 1 2 3 4 5 -0.2 -0.4 -0.6 2nd derivative Peak is at the inflection Of first derivative – should Be symmetrical for normal Population; goes to zero at Std. dev. -0.8 -1 s 1st derivative, Peak is at the inflection Determines the std. dev. Asymmetry can be determined from principle component analysis A. F. (≠Alanah Fitch) = asymmetric factor Comparing TWO populations of measurements 146 School Begins 145 Baseline Vacation weight (lbs) 144 143 142 141 140 139 0 10 20 30 Day 40 50 60 Is there a difference between my “baseline” weight and school weight? Can you “detect” a difference? Can you “quantitate” a difference? Exact same information displayed differently, but now we divide The data into different measurement populations 25 school # of Observations 20 15 10 baseline 5 0 138 139 140 141 142 143 Weight (lbs) Model of the data as two normal populations 144 145 146 147 25 146 145 144 weight (lbs) # of Observations 20 15 143 142 141 140 139 0 10 20 30 40 50 60 Standard deviation Of the school weigh Day 10 Standard deviation Of baseline weight 5 0 138 139 140 141 Average Baseline weight 142 143 Weight (lbs) 144 145 146 Average school weight 147 25 20 20 # of Observations 15 10 15 10 5 5 0 138 0 139 140 141 142 Weight (lbs) 143 144 145 146 147 Weight (lbs) We have two models to describe the population of measurements Of my weight. In one we assume that all measurements fall into a single population. In the second we assume that the measurements Have sampled two different populations. 25 20 Which is the better model? How to we quantify “better”? # of Observations # of Observations 25 15 10 5 0 138 139 140 141 142 143 Weight (lbs) 144 145 146 147 25 The red bars represent the difference Between the two population model and The data # of Observations 20 15 10 5 Compare how close The measured data Fits the model The purple lines represent The difference between The single population Model and the data Which model Has less summed differences? 0 138 139 140 141 142 143 Weight (lbs) Did I gain weight? 144 145 146 147 Normally sum the square of the difference in order to account for Both positive and negative differences. This process (summing of the squares of the differences) Is essentially what occurs in an ANOVA Analysis of variance In the bad old days you had to work out all the sums of squares. In the good new days you can ask Excel program to do it for you. Anova: Single Factor 5% certainty SUMMARY Groups Count Column 1 12 Column 2 12 ANOVA Source of Variation Between Groups Within Groups SS 194.4273 167.2408 Total 361.6682 Sum Average 277.41 23.1175 345.72 28.81 df MS 1 194.4273 22 7.601856 Variance 8.70360227 6.50010909 F P-value F crit 25.5762995 4.59E-05 4.300949 Source of Variation 23 Test: is F<Fcritical? If true = hypothesis true, single population if false = hypothesis false, can not be explained by a single population at the 5% certainty level 0.3 0.35 Red, N=12, Sum sq diff=0.11, stdev=3.27 White, N=12, Sum sq diff=0.037, stdev=2.55 Red, N=40, Sum sq diff=0.017, stdev-2.67 White, N=38, Sum sq diff=0.028, stdev=2.15 N=24 Sum sq diff=0.0449, stdev=3.96 N=78, sum sq diff=0.108, stdev=4.05 0.3 0.25 0.25 Frequency Frequency 0.2 0.2 0.15 0.15 0.1 0.1 0.05 0.05 0 0 14 19 24 29 Length (cm) 34 39 14 19 24 29 34 39 Length, cm In an Analysis of Variance you test the hypothesis that the sample is Best described as a single population. 1. Create the expected frequency (Gaussian from normal error curve) 2. Measure the deviation between the histogram point and the expected frequency 3. Square to remove signs 4. SS = sum squares 5. Compare to expected SS which scales with population size 6. If larger than expected then can not explain deviations assuming a single population 0.3 0.35 Red, N=12, Sum sq diff=0.11, stdev=3.27 White, N=12, Sum sq diff=0.037, stdev=2.55 Red, N=40, Sum sq diff=0.017, stdev-2.67 White, N=38, Sum sq diff=0.028, stdev=2.15 N=24 Sum sq diff=0.0449, stdev=3.96 N=78, sum sq diff=0.108, stdev=4.05 0.3 0.25 0.25 Frequency 0.2 0.15 0.15 0.1 0.1 0.05 0.05 0 0 14 19 24 29 34 14 39 19 24 29 34 39 Length, cm Length (cm) 0.04 0.035 Square Difference Expected Measured Frequency 0.2 0.03 0.025 0.02 0.015 0.01 0.005 0 15 17 19 21 23 25 Length (cm) 27 29 31 33 35 The square differences For an assumption of A single population Is larger than for The assumption of Two individual populations There are other measurements which describe the two populations Resolution of two peaks xa xb R Wa Wb 2 2 Mean or average Baseline width x a xb 4.5 xa xb 4 3.5 Signal Wa Wb 3 2 2.5 2 2 1.5 Wa 2 1 Wb 2 0.5 0 1 1.5 In this example R 1: Wa Wb xa xb 2 2 2 2.5 3 3.5 4 x Peaks are baseline resolved when R > 1 x a xb 1.8 xa xb 1.6 1.4 Signal Wa Wb 1.2 2 12 0.8 0.6 Wa 2 0.4 Wb 2 0.2 0 1 1.5 In this example R 1: 2 Wa Wb xa xb 2 2 2.5 x 3 3.5 Peaks are just baseline resolved when R = 1 4 x a xb 1.6 xa xb 1.4 1.2 Signal Wa Wb 1 2 2 0.8 0.6 Wa 2 0.4 0.2 Wb 2 0 1 1.5 In this example R 1: 2 Wa Wb xa xb 2 2 2.5 3 3.5 x Peaks are not baseline resolved when R < 1 4 2008 Data 0.35 White, N=12, Sum sq diff=0.037 Red, N=12, Sum sq diff=0.11 0.3 xp Frequency 0.25 0.2 1 2 W R WW R1 0.15 0.1 0.05 0 14 19 24 29 Length (cm) What is the R for this data? 34 39 Comparison of 1978 Low Lead to 1978 High Lead 25 20 Comparison of 1978 Low Lead to 1979 High Lead 25 % Measured 20 15 15 10 10 5 5 0 0 0 0 20 40 60 80 100 120 140 20 160 40 60 80 Series2 100 120 140 Series3 IQ Verbal Visually less resolved Anonymous 2009 student analysis of Needleman data Wa ~ 112 ~ 70 42 2 Wb ~ 130 ~ 95 35 2 R xa xb Wa Wb 2 2 Visually better resolved 160 Comparison of 1978 Low Lead to 1978 High Lead 25 20 Comparison of 1978 Low Lead to 1979 High Lead 25 % Measured 20 15 15 10 10 5 5 0 0 0 0 20 40 60 80 100 120 140 20 40 60 80 Series2 160 100 120 140 Series3 IQ Verbal Visually less resolved Visually better resolved Anonymous 2009 student analysis of Needleman data Wa ~ 112 ~ 70 42 2 Wb ~ 130 ~ 95 35 2 x a x b ~ 112 ~ 95 17 R xa xb 17 ~ 0.22 Wa Wb 42 35 2 2 160 Other measures of the quality of separation of the Peaks 1. Limit of detection 2. Limit of quantification 3. Signal to noise (S/N) X blank X limit of detection 0.45 99.74% Of the observations Of the blank will lie below the mean of the First detectable signal (LOD) 0.4 0.35 Amplitude 0.3 0.25 0.2 0.15 0.1 0.05 0 -6 -4 -2 0 x LOD xblank 3sblank 2 3s 4 s 6 8 10 12 Two peaks are visible when all the data is summed together 0.45 0.4 0.35 Amplitude 0.3 0.25 0.2 0.15 0.1 0.05 0 -6 -4 -2 0 2 3s s 4 6 8 10 12 146 25 # of Observations 20 145 15 10 5 144 0 138 139 140 141 142 143 144 145 146 147 weight (lbs) Weight (lbs) 143 142 141 140 139 0 10 20 30 Day Estimate the LOD (signal) of this data 40 50 60 Other measures of the quality of separation of the Peaks 1. Limit of detection 2. Limit of quantification 3. Signal to noise (S/N) x LOQ xblank 9sblank Your book suggests 10 0.45 0.4 0.35 Amplitude 0.3 0.25 0.2 0.15 0.1 0.05 0 -6 -4 -2 0 2 4 6 8 9s 10 12 Limit of squantification requires absolute Certainty that no blank is part of the 146 25 # of Observations 20 145 15 10 5 144 0 138 139 140 141 142 143 144 145 146 147 weight (lbs) Weight (lbs) 143 142 141 140 139 0 10 20 30 Day Estimate the LOQ (signal) of this data 40 50 60 Other measures of the quality of separation of the Peaks 1. Limit of detection 2. Limit of quantification 3. Signal to noise (S/N) Signal = xsample - xblank Noise = N = standard deviation, s x sample xblank x sample xblank S N s pp 6 (This assumes pp school ~ pp baseline) 146 25 # of Observations 20 145 School Begins 15 Baseline Vacation 10 5 144 0 138 139 140 141 142 143 144 145 146 147 weight (lbs) Weight (lbs) 143 Peak to peak variation within mean school ~ 6s where s = N for Noise 142 Signal 141 140 139 0 10 20 30 Estimate the S/N of this data Day 40 50 60 35 30 length (cm) 25 20 15 Can you “tell” where the switch between Red and white potatoes begins? 10 What is the signal (length of white)? What is the background (length of red)? What is the S/N ? 5 0 0 5 10 15 Sample number 20 25 30 Effect of sample size on the measurement Error curve Peak height grows with # of measurements. + - 1 s always has same proportion of total number of measurements However, the actual value of s decreases as population grows ssample s population nsample 2008 Data 27 5 4.5 4 26 3 25 2.5 24.5 2 24 Red Running Stdev 3.5 25.5 ssample 1.5 23.5 1 23 0.5 22.5 s population nsample 0 0 2 4 6 8 10 12 14 Sample number 4.1 3.9 3.7 stdev red length cm Red Running Length Average 26.5 3.5 3.3 3.1 y = -0.8807x + 5.9303 R2 = 0.9491 2.9 2.7 2.5 1.5 2 2.5 3 sqrt number of samples 3.5 4 0.35 Red, N=12, Sum sq diff=0.11, stdev=3.27 White, N=12, Sum sq diff=0.037, stdev=2.55 Red, N=40, Sum sq diff=0.017, stdev-2.67 White, N=38, Sum sq diff=0.028, stdev=2.15 0.3 Frequency 0.25 0.2 0.15 0.1 0.05 0 14 19 24 29 Length (cm) 34 39 Calibration Curve A calibration curve is based on a selected measurement as linear In response to the concentration of the analyte. y a bx Or… a prediction of measurement due to some change Can we predict my weight change if I had spent a longer time on Vacation? fitch lbs a bdays on vacation 25 # of Observations 20 15 10 5 0 138 139 140 141 142 143 Weight (lbs) 144 145 146 147 5 days fitch lbs a bdays on vacation The calibration curve contains information about the sampling Of the population 143 Can get this by using “trend line” 142.5 Fitch Weight, lbs 142 y = 0.3542x + 140.04 2 R = 0.7425 141.5 141 140.5 140 139.5 139 0 1 2 3 Days on Vacation 4 5 6 This is just a trendline From “format” data 4.1 3.9 stdev red length cm 3.7 3.5 3.3 3.1 y = -0.8807x + 5.9303 R2 = 0.9491 2.9 2.7 Sample 1 2 3 4 5 6 7 8 9 10 11 12 sqrt(#samples) 1 1.414213562 1.732050808 2 2.236067977 2.449489743 2.645751311 2.828427125 3 3.16227766 3.31662479 3.464101615 stdev #DIV/0! 2.036468 4.475727 4.31441 3.844045 3.844604 3.735124 3.458414 3.235055 3.093053 2.935944 2.950187 2.5 1.5 2 2.5 3 3.5 4 sqrt number of samples SUMMARY OUTPUT Regression Statistics Multiple R 0.296113395 R Square 0.087683143 Adjusted R Square -0.013685397 Standard Error 0.703143388 Observations 11 Using the analysis Data pack ANOVA df Regression Residual Total Intercept X Variable 1 1 9 10 Coefficients 3.884015711 -0.06235252 SS MS F Significance F 0.427662048 0.427662 0.864994 0.376617 4.449695616 0.494411 4.877357664 Standard Error t Stat P-value Lower 95% 0.514960076 7.542363 3.53E-05 2.719094 0.067042092 -0.93005 0.376617 -0.21401 Get an error Associated with The intercept In the best of all worlds you should have a series of blanks That determine you’re the “noise” associated with the background x LOD xblank 3sblank Sometimes you forget, so to fall back and punt, estimate The standard deviation of the “blank” from the linear regression But remember, in doing this you are acknowledging A failure to plan ahead in your analysis x LOD x blank b[conc. LOD] Signal LOD Sensitivity (slope) x LOD xblank 3sblank x blank 3sblank x blank b[conc. LOD] 3sblank [conc. LOD] b Extrapolation of the associated error Can be obtained from the Linear Regression data The concentration LOD depends on BOTH Stdev of blank and sensitivity !!Note!! Signal LOD ≠ Conc LOD We want Conc. LOD Selectivity pHpM or pM pH or 0 0 12 12 10 10 8 8 6 6 4 4 2 2 0 0 Difference in slope is one measure selectivity -50 -50 Pb2+ y = -31.143x - 74.333 R2 = 0.9994 mV -150 + -150 H -200-200 -250-250 y = -41x - 118.5 R2 = 0.9872 In a perfect method the sensing device would have zero Slope for the interfering species -300-300 -350-350 mV -100-100 Limit of linearity 5% deviation Summary: Figures of Merit Thus far R = resolution S/N LOD = both signal and concentration Can be expressed in terms of signal, but better LOQ Expression is in terms of concentration LOL Sensitivity (calibration curve slope) Selectivity (essentially difference in slopes) Tests: Anova Why is the limit of detection important? Why has the limit of detection changed so much in the Last 20 years? The End 25 20 20 % of Measurements % of Measurements 25 15 10 15 10 5 5 0 0 40 60 80 100 120 Verbal IQ 140 160 40 60 80 100 120 140 Verbal IQ Which of these two data sets would be likely To have better numerical value for the Ability to distinguish between two different Populations? Needleman’s data 160 Height for normalized Bell curve <1 2008 Data 0.35 White, N=12, Sum sq diff=0.037 Red, N=12, Sum sq diff=0.11 0.3 Frequency 0.25 0.2 0.15 0.1 0.05 0 14 19 24 29 Length (cm) Which population is more variable? How can you tell? 34 39 0.35 Red, N=12, Sum sq diff=0.11, stdev=3.27 White, N=12, Sum sq diff=0.037, stdev=2.55 Red, N=40, Sum sq diff=0.017, stdev-2.67 White, N=38, Sum sq diff=0.028, stdev=2.15 0.3 Frequency 0.25 0.2 0.15 0.1 0.05 0 14 19 24 29 34 39 Length (cm) Increasing the sample size decreases the std dev and increases separation Of the populations, notice that the means also change, will do so until We have a reasonable sample of the population 25 % of Measurements 20 15 10 5 0 40 60 80 100 Verbal IQ 120 140 160 25 % of Measurements 20 15 10 5 0 40 60 80 100 Verbal IQ 120 140 160 ELEMENTARY MARIO F. TRIOLA STATISTICS EIGHTH EDITION Chapter 1 Introduction to Statistics 1-1 Overview 1-2 The Nature of Data 1-3 Uses and Abuses of Statistics 1-4 Design of Experiments Chapter 2 Describing, Exploring, and Comparing Data 2-1 Overview 2-2 Summarizing Data with Frequency Tables 2-3 Pictures of Data 2-4 Measures of Center 2-5 Measures of Variation 2-6 Measures of Position 2-7 Exploratory Data Analysis (EDA) Chapter 3 Probability 3-1 Overview 3-2 Fundamentals 3-3 Addition Rule 3-4 Multiplication Rule: Basics 3-5 Multiplication Rule: Complements and Conditional Probability 3-6 Counting Chapter 4 Probability Distributions 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, and Standard Deviation for the Binomial Distribution Chapter 5 Normal Probability Distributions 5-1 Overview 5-2 The Standard Normal Distribution 5-3 Nonstandard Normal Distributions: Finding Probabilities 5-4 Nonstandard Normal Distributions: Finding Values 5-5 The Central Limit Theorem 5-6 Normal Distribution as Approximation to Binomial Distribution Chapter 6 Estimates and Sample Sizes 6-1 Overview 6-2 Estimating a Population Mean: Large Samples 6-3 Estimating a Population Mean: Small Samples 6-4 Determining Sample Size 6-5 Estimating a Population Proportion 6-6 Estimating a Population Variance Chapter 7 Hypothesis Testing 7-1 Overview 7-2 Fundamentals of Hypothesis Testing 7-3 Testing a Claim about a Mean: Large Samples 7-4 Testing a Claim about a Mean: Small Samples 7-5 Testing a Claim about a Proportion 7-6 Testing a Claim about a Standard Deviation or Variance Chapter 8 Inferences from Two Samples 8-1 Overview 8-2 Inferences about Two Means: Independent and Large Samples 8-3 Inferences about Two Means: Matched Pairs 8-4 Inferences about Two Proportions Chapter 9 Correlation and Regression 9-1 Overview 9-2 Correlation 9-3 Regression 9-4 Variation and Prediction Intervals 9-5 Rank Correlation Chapter 10 Multinomial Experiments and Contingency Tables 10-1 Overview 10-2 Multinomial Experiments: Goodness-0f-Fit 10-3 Contingency Tables: Independence and Homogeneity 10-4 One-Way ANOVA ELEMENTARY Chapter 1 STATISTICS Introduction to Statistics MARIO F. TRIOLA EIGHTH EDITION Chapter 1 Introduction to Statistics 1-1 Overview 1-2 The Nature of Data 1-3 Uses and Abuses of Statistics 1-4 Design of Experiments 1-1 Overview Statistics Two Meanings Specific numbers Method of analysis Statistics Specific number numerical measurement determined by a set of data Example: Twenty-three percent of people polled believed that there are too many polls. Statistics Method of analysis a collection of methods for planning experiments, obtaining data, and then then organizing, summarizing, presenting, analyzing, interpreting, and drawing conclusions based on the data Definitions Population the complete collection of all elements (scores, people, measurements, and so on) to be studied. The collection is complete in the sense that it includes all subjects to be studied. Definitions Census the collection of data from every element in a population Sample a subcollection of elements drawn from a population 1-2 The Nature of Data Definitions Parameter a numerical measurement describing some characteristic of a population Definitions Parameter a numerical measurement describing some characteristic of a population population parameter Definitions Statistic a numerical measurement describing some characteristic of a sample Definitions Statistic a numerical measurement describing some characteristic of a sample sample statistic Definitions Quantitative data numbers representing counts or measurements Definitions Quantitative data numbers representing counts or measurements Qualitative (or categorical or attribute) data can be separated into different categories that are distinguished by some nonnumeric characteristics Definitions Quantitative data the incomes of college graduates Definitions Quantitative data the incomes of college graduates Qualitative (or categorical or attribute) data the genders (male/female) of college graduates Definitions Discrete data result when the number of possible values is either a finite number or a ‘countable’ number of possible values 0, 1, 2, 3, . . . Definitions Discrete data result when the number of possible values is either a finite number or a ‘countable’ number of possible values 0, 1, 2, 3, . . . Continuous (numerical) data result from infinitely many possible values that correspond to some continuous scale that 2covers a range of 3 values without gaps, interruptions, Definitions Discrete The number of eggs that hens lay; for example, 3 eggs a day. Definitions Discrete The number of eggs that hens lay; for example, 3 eggs a day. Continuous The amounts of milk that cows produce; for example, 2.343115 gallons a day. Definitions nominal level of measurement characterized by data that consist of names, labels, or categories only. The data cannot be arranged in an ordering scheme (such as low to high) Example: survey responses yes, no, undecided Definitions ordinal level of measurement involves data that may be arranged in some order, but differences between data values either cannot be determined or are meaningless Example: Course grades A, B, C, D, or F Definitions interval level of measurement like the ordinal level, with the additional property that the difference between any two data values is meaningful. However, there is no natural zero starting point (where none of the quantity is present) Example: Years 1000, 2000, 1776, and 1492 Definitions ratio level of measurement the interval level modified to include the natural zero starting point (where zero indicates that none of the quantity is present). For values at this level, differences and ratios are meaningful. Example: Prices of college textbooks Levels of Measurement Nominal - categories only Ordinal - categories with some order Interval - differences but no natural starting point Ratio - differences and a natural starting point Levels of Measurement Nominal - categories only Ordinal - categories with some order Interval - differences but no natural starting point Ratio - differences and a natural starting point ELEMENTARY STATISTICS Section 1-3 Uses and Abuses of Statistics MARIO F. TRIOLA EIGHTH EDITION Uses of Statistics Almost all fields of study benefit from the application of statistical methods Abuses of Statistics Bad Samples Definitions self-selected survey (or voluntary response sample) one in which the respondents themselves decide whether to be included Abuses of Statistics Bad Samples Small Samples Loaded Questions Misleading Graphs Figure 1-1 Salaries of People with Bachelor’s Degrees and with High School Diplomas $40,500 $40,500 $40,000 $40,000 35,000 30,000 30,000 20,000 25,000 $24,400 20,000 $24,400 10,000 0 Bachelor High School Degree Diploma (a) Bachelor High Schoo Degree(b) Diploma We should analyze the numerical information given in the graph instead of being mislead by its general shape. Abuses of Statistics Bad Samples Small Samples Loaded Questions Misleading Graphs Pictographs Double the length, width, and height of a cube, and the volume increases by a factor of eight Figure 1-2 Abuses of Statistics Bad Samples Small Samples Loaded Questions Misleading Graphs Pictographs Precise Numbers Distorted Percentages Partial Pictures “Ninety percent of all our cars sold in this country in the last 10 years are still on the road.” Abuses of Statistics Bad Samples Small Samples Loaded Questions Misleading Graphs Pictographs Precise Numbers Distorted Percentages Partial Pictures Deliberate Distortions ELEMENTARY Section 1-4 MARIO F. TRIOLA STATISTICS Design of Experiments EIGHTH EDITION Definitions Observational Study observing and measuring specific characteristics without attempting to modify the subjects being studied Definitions Experiment apply some treatment and then observe its the subjects effects on Designing an Experiment Identify your objective Collect sample data Use a random procedure that avoids bias Analyze the data and form conclusions Definitions Confounding occurs in an experiment when the effects from two or more variables cannot be distinguished from each other Definitions Replication used when an experiment is repeated on a sample of subjects that is large enough so that we can see the true nature of any effects (instead of being misled by erratic behavior of samples that are too small) Definitions Random Sample members of the population are selected in such a way that each has an equal chance of being selected Definitions Random Sample members of the population are selected in such a way that each has an equal chance of being selected Simple Random Sample (of size n) subjects selected in such a way that every possible sample of size n has the same chance of being chosen Random Sampling - selection so that each has an equal chance of being selected Systematic Sampling - Select some starting point and then select every K th element in the population Convenience Sampling - use results that are readily available Hey! Do you believe in the death penalty? Stratified Sampling - subdivide the population into subgroups that share the same characteristic, then draw a sample from each stratum Cluster Sampling - divide the population into sections (or clusters); randomly select some of those clusters; choose all members from selected clusters Methods of Sampling Random Systematic Convenience Stratified Cluster Definitions Sampling Error the difference between a sample result and the true population result; such an error results from chance sample fluctuations. Nonsampling Error sample data that are incorrectly collected, recorded, or analyzed (such as by selecting a biased sample, using a defective instrument, or copying the data incorrectly). STATISTICS ELEMENTARY Chapter 2 Descriptive Statistics MARIO F. TRIOLA EIGHTH EDITION Chapter 2 Descriptive Statistics 2-1 Overview 2-2 Summarizing Data with Frequency Tables 2-3 Pictures of Data 2-4 Measures of Center 2-5 Measures of Variation 2-6 Measures of Position 2-7 Exploratory Data Analysis (EDA) 2 -1 Overview Descriptive Statistics summarize or describe the important characteristics of a known set of population data Inferential Statistics use sample data to make inferences (or generalizations) about a population Important Characteristics of Data 1. Center: A representative or average value that indicates where the middle of the data set is located 2. Variation: A measure of the amount that among themselves the values vary 3. Distribution: The nature or shape of the distribution of data (such as bell-shaped, uniform, or skewed) 4. Outliers: Sample values that lie very far away from the vast majority of other sample values 5. Time: Changing characteristics of the data over time 2-2 Summarizing Data With Frequency Tables Frequency Table lists classes (or categories) of values, along with frequencies (or counts) of the number of values that fall into each class Table 2-1 Qwertry Keyboard Word Ratings 2 2 5 1 2 6 3 3 4 2 4 0 5 7 7 5 6 6 8 10 7 2 2 10 5 8 2 5 4 2 6 2 6 1 7 2 7 2 3 8 1 5 2 5 2 14 2 2 6 3 1 7 Table 2-3 Frequency Table of Qwerty Word Ratings Rating Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Frequency Table Definitions Lower Class Limits are the smallest numbers that can actually belong to different classes Lower Class Limits are the smallest numbers that can actually belong to different classes Rating Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Lower Class Limits are the smallest numbers that can actually belong to different classes Rating Lower Class Limits Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Upper Class Limits are the largest numbers that can actually belong to different classes Upper Class Limits are the largest numbers that can actually belong to different classes Rating Upper Class Limits Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Class Boundaries are the numbers used to separate classes, but without the gaps created by class limits Class Boundaries number separating classes Rating Frequency - 0.5 0-2 20 2.5 3-5 5.5 14 6-8 15 8.5 9 - 11 2 12 11.5- 14 1 14.5 Class Boundaries number separating classes Rating Frequency - 0.5 0-2 20 2.5 Class Boundaries 3-5 5.5 14 6-8 15 8.5 9 - 11 2 12 11.5- 14 1 14.5 Class Midpoints midpoints of the classes Class Midpoints midpoints of the classes Rating Class Midpoints Frequency 0- 1 2 20 3- 4 5 14 6- 7 8 15 9 - 10 11 2 12 - 13 14 1 Class Width is the difference between two consecutive lower class limits or two consecutive class boundaries Class Width is the difference between two consecutive lower class limits or two consecutive class boundaries Rating Class Width Frequency 3 0-2 20 3 3-5 14 3 6-8 15 3 9 - 11 2 3 12 - 14 1 Guidelines For Frequency Tables 1. Be sure that the classes are mutually exclusive. 2. Include all classes, even if the frequency is zero. 3. Try to use the same width for all classes. 4. Select convenient numbers for class limits. 5. Use between 5 and 20 classes. 6. The sum of the class frequencies must equal the original data values. number of Constructing A Frequency Table 1. Decide on the number of classes . 2. Determine the class width by dividing the range by the number classes (range = highest score - lowest score) and round up. class width 3. round up of of range number of classes Select for the first lower limit either the lowest score or a convenient value slightly less than the lowest score. 4. Add the class width to the starting point to get the second lower class limit, add the width to the second lower limit to get the third, and so on. 5. List the lower class limits in a vertical column and enter the upper class limits. 6. Represent each score by a tally mark in the appropriate class. Total tally marks to find the total frequency for each class. Figure 2-1 Relative Frequency Table class frequency relative frequency = sum of all frequencies Relative Frequency Table Rating Frequency Relative Rating Frequency 0-2 20 0-2 38.5% 3-5 14 3-5 26.9% 6-8 15 6-8 28.8% 9 - 11 2 9 - 11 3.8% 12 - 14 1 12 - 14 1.9% Total frequency = 52 Table 2-5 20/52 = 38.5% 14/52 = 26.9% etc. Cumulative Frequency Table Rating Frequency Cumulative Frequency Rating 0-2 20 Less than 3 20 3-5 14 Less than 6 34 6-8 15 Less than 9 49 9 - 11 2 Less than 12 51 12 - 14 1 Less than 15 52 Table 2-6 Cumulative Frequencies Frequency Tables Rating Frequency Rating Relative Frequency Cumulative Frequency Rating 0-2 20 0-2 38.5% Less than 3 20 3-5 14 3-5 26.9% Less than 6 34 6-8 15 6-8 28.8% Less than 9 49 9 - 11 2 9 - 11 3.8% Less than 12 51 12 - 14 1 12 - 14 1.9% Less than 15 52 Table 2-3 Table 2-5 Table 2-6 STATISTICS ELEMENTARY Section 2-3 Pictures of Data MARIO F. TRIOLA EIGHTH EDITION Pictures of Data depict the nature or shape of the data distribution Histogram a bar graph in which the horizontal scale represents classes and the vertical scale represents frequencies Table 2-3 Frequency Table of Qwerty Word Ratings Rating Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Histogram of Qwerty Word Ratings Figure 2-2 Rating Frequency 0-2 20 3-5 14 6-8 15 9 - 11 2 12 - 14 1 Relative Frequency Histogram of Qwerty Word Ratings Rating Relative Frequency 0-2 38.5% 3-5 26.9% 6-8 28.8% 9 - 11 3.8% 12 - 14 1.9% Figure 2-3 Histogram and Relative Frequency Histogram Figure 2-2 Figure 2-3 Frequency Polygon Figure 2-4 Ogive Figure 2-5 Dot Plot Figure 2-6 Stem-and Leaf Plot Stem Raw Data (Test Grades) 67 72 85 75 89 89 88 90 99 100 6 7 8 9 10 Leaves 7 25 5899 09 0 Pareto Chart 45,000 40,000 35,000 30,000 Accidental Deaths by Type Frequency 25,000 20,000 15,000 10,000 5,000 Firearms Ingestion of food or object Fire Poison Falls Drowning Figure 2-7 Motor Vehicle 0 Pie Chart Firearms (1400. 1.9%) Ingestion of food or object (2900. 3.9% Fire (4200. 5.6%) Motor vehicle (43,500. 57.8%) Drowning (4600. 6.1%) Poison (6400. 8.5%) Figure 2-8 Accidental Deaths by Type Falls (12,200. 16.2%) Scatter Diagram 20 TAR • 10 • • • • • • • • • • • • • • • • • • • • 0 0.0 0.5 1.0 NICOTINE 1.5 Deaths in British Military Hospitals During the Crimean War Figure 2-9 Other Graphs Boxplots (textbook section 2-7) Pictographs Pattern of data over time STATISTICS ELEMENTARY Section 2-4 Measures of Center MARIO F. TRIOLA EIGHTH EDITION Measures of Center a value at the center or middle of a data set Definitions Mean (Arithmetic Mean) AVERAGE the number obtained by adding the values and dividing the total by the number of values Notation denotes the addition of a set of values is the variable usually used to represent the individual data values x n represents the number of data values in a sample N represents the number of data values in a population Notation pronounced ‘x-bar’ and denotes the mean of a set of x issample values x x = n Notation pronounced ‘x-bar’ and denotes the mean of a set of x issample values x x = n µ is pronounced ‘mu’ and denotes the mean of all values in a population µ = x N Calculators can calculate the mean of data Definitions Median the middle value when the original data values are arranged in order of increasing (or decreasing) magnitude Definitions Median the middle value when the original data values are arranged in order of increasing (or decreasing) magnitude often denoted by x ~ (pronounced ‘x-tilde’) Definitions Median the middle value when the original data values are arranged in order of increasing (or decreasing) magnitude often denoted by x ~ (pronounced ‘x-tilde’) is not affected by an extreme value 6.72 3.46 3.60 6.44 3.46 3.60 6.44 6.72 (even number of values) no exact middle -- shared by two numbers 3.60 + 6.44 2 MEDIAN is 5.02 6.72 3.46 3.60 6.44 3.46 3.60 6.44 6.72 (even number of values) no exact middle -- shared by two numbers 3.60 + 6.44 MEDIAN is 5.02 2 6.72 3.46 3.60 6.44 26.70 3.46 3.60 6.44 6.72 26.70 (in order exact middle odd number of values) MEDIAN is 6.44 Definitions Mode the score that occurs most frequently Bimodal Multimodal No Mode denoted by M the only measure of central tendency that can be used with nominal data Examples a. 5 5 5 3 1 5 1 4 3 5 Mode is 5 b. 1 2 2 2 3 4 5 6 6 6 7 9 Bimodal - c. 1 2 3 6 7 8 9 10 and 6 No Mode 2 Definitions Midrange the value midway between the highest lowest values in the original data set and Definitions Midrange the value midway between the highest lowest values in the original data set highest score + lowest score Midrange = 2 and Round-off Rule for Measures of Center Carry one more decimal place than is present in the original set of values Mean from a Frequency Table use class midpoint of classes for variable x Mean from a Frequency Table use class midpoint of classes for variable x (f • x) x = f Formula 2-2 Mean from a Frequency Table use class midpoint of classes for variable x (f • x) x = f Formula 2-2 x = class midpoint f = frequency f=n Weighted Mean (w • x) x = w Best Measure of Center Advantages - Disadvantages Table 2-13 Definitions Symmetric Data is symmetric if the left half of its histogram is roughly a mirror of its right half. Skewed Data is skewed if it is not symmetric and if it extends more to one side than the other. Skewness Figure 2-13 (b) Mode = Mean = Median SYMMETRIC Skewness Figure 2-13 (b) Mode = Mean = Median SYMMETRIC Mean Mode Median Figure 2-13 (a) SKEWED LEFT (negatively) Skewness Figure 2-13 (b) Mode = Mean = Median SYMMETRIC Mean Mode Median Figure 2-13 (a) SKEWED LEFT (negatively) Mean Mode Median SKEWED RIGHT (positively) Figure 2-13 (c) STATISTICS ELEMENTARY Section 2-5 Measures of Variation MARIO F. TRIOLA EIGHTH EDITION Waiting Times of Bank Customers at Different Banks in minutes Jefferson Valley Bank 6.5 6.6 6.7 6.8 7.1 7.3 7.4 7.7 7.7 7.7 Bank of Providence 4.2 5.4 5.8 6.2 6.7 7.7 7.7 8.5 9.3 10.0 Waiting Times of Bank Customers at Different Banks in minutes Jefferson Valley Bank 6.5 6.6 6.7 6.8 7.1 7.3 7.4 7.7 7.7 7.7 Bank of Providence 4.2 5.4 5.8 6.2 6.7 7.7 7.7 8.5 9.3 10.0 Jefferson Valley Bank Bank of Providence Mean 7.15 7.15 Median 7.20 7.20 Mode 7.7 7.7 Midrange 7.10 7.10 Dotplots of Waiting Times Figure 2-14 Measures of Variation Measures of Variation Range highest value lowest value Measures of Variation Standard Deviation a measure of variation of the scores about the mean (average deviation from the mean) Sample Standard Deviation Formula Sample Standard Deviation Formula S= (x - x) n-1 2 Formula 2-4 calculators can compute the sample standard deviation of data Sample Standard Deviation Shortcut Formula n (x ) - (x) n (n - 1) 2 s= Formula 2-5 calculators can compute the sample standard deviation of data 2 Mean Deviation Formula (absolute deviation) Mean Absolute Deviation Formula x-x n Population Standard Deviation s = (x - µ) 2 N calculators can compute the population standard deviation of data Symbols for Standard Deviation Symbols for Standard Deviation Sample Symbols for Standard Deviation Sample s Symbols for Standard Deviation Sample Textbook s Symbols for Standard Deviation Sample Textbook s Sx Symbols for Standard Deviation Sample Textbook Some graphics calculators s Sx Symbols for Standard Deviation Sample Textbook Some graphics calculators s Sx xsn-1 Symbols for Standard Deviation Sample Textbook Some graphics calculators Some non-graphics calculators s Sx xsn-1 Symbols for Standard Deviation Sample Textbook Some graphics calculators Some non-graphics calculators s Sx xsn-1 Population Symbols for Standard Deviation Sample Textbook Some graphics calculators Some non-graphics calculators Population s s Sx sx xsn xsn-1 Symbols for Standard Deviation Sample Textbook Some graphics calculators Some non-graphics calculators Population s s Sx sx xsn xsn-1 Book Some graphics calculators Some non-graphics calculators Symbols for Standard Deviation Sample Textbook Some graphics calculators Some non-graphics calculators Population s s Sx sx xsn xsn-1 Book Some graphics calculators Some non-graphics calculators Articles in professional journals and reports often use SD for standard deviation and VAR for variance. Measures of Variation Variance Measures of Variation Variance standard deviation squared Measures of Variation Variance standard deviation squared Notation } s s 2 2 use square key on calculator Variance 2 s = s 2 = (x - x ) 2 n-1 (x - µ) N 2 Sample Variance Population Variance Round-off Rule for measures of variation Carry one more decimal place than is present in the original set of values. Round only the final answer, never in the middle of a calculation. Standard Deviation from a Frequency Table Formula 2-6 n [(f • x 2)] -[(f • x)]2 S= n (n - 1) Use the class midpoints as the x values Calculators can compute the standard deviation for frequency table Estimation of Standard Deviation Range Rule of Thumb x - 2s (minimum usual value) x + 2s x Range or (maximum usual value) 4s Estimation of Standard Deviation Range Rule of Thumb x - 2s (minimum usual value) Range or s x + 2s x Range 4 (maximum usual value) 4s Estimation of Standard Deviation Range Rule of Thumb x - 2s x + 2s x (minimum usual value) Range (maximum usual value) 4s or s Range 4 = highest value - lowest value 4 Usual Sample Values Usual Sample Values minimum ‘usual’ value (mean) - 2 (standard deviation) minimum x - 2(s) Usual Sample Values minimum ‘usual’ value (mean) - 2 (standard deviation) minimum x - 2(s) maximum ‘usual’ value (mean) + 2 (standard deviation) maximum x + 2(s) FIGURE 2-15 The Empirical Rule (applies to bell-shaped distributions) x FIGURE 2-15 The Empirical Rule (applies to bell-shaped distributions) 68% within 1 standard deviation 34% x-s 34% x x+s The Empirical Rule FIGURE 2-15 (applies to bell-shaped distributions) 95% within 2 standard deviations 68% within 1 standard deviation 34% 34% 13.5% x - 2s 13.5% x-s x x+s x + 2s The Empirical Rule FIGURE 2-15 (applies to bell-shaped distributions) 99.7% of data are within 3 standard deviations of the mean 95% within 2 standard deviations 68% within 1 standard deviation 34% 34% 2.4% 2.4% 0.1% 0.1% 13.5% x - 3s x - 2s 13.5% x-s x x+s x + 2s x + 3s Chebyshev’s Theorem applies to distributions of any shape. the proportion (or fraction) of any set of data lying within K standard deviations of the mean is always at 2 least 1 - 1/K , where K is any positive number greater than 1. at least 3/4 (75%) of all values lie within 2 standard deviations of the mean. at least 8/9 (89%) of all values lie within 3 standard deviations of the mean. Measures of Variation Summary For typical data sets, it is unusual for a score to differ from the mean by more than 2 or 3 standard deviations. STATISTICS ELEMENTARY Section 2-6 Measures of Position MARIO F. TRIOLA EIGHTH EDITION Measures of Position Measures of Position z Score (or standard score) the number of standard deviations that a given value x is above or below the mean Measures of Position z score Sample x x z= s Measures of Position z score Sample x x z= s Population x µ z= s Measures of Position z score Sample x x z= s Population x µ z= s Round to 2 decimal places FIGURE 2-16 Interpreting Z Scores Unusual Values Ordinary Values -3 -2 -1 0 Z Unusual Values 1 2 3 Measures of Position Quartiles, Deciles, Percentiles Quartiles Quartiles Q1, Q2, Q3 Quartiles Q1, Q2, Q3 divides ranked scores into four equal parts Quartiles Q1, Q2, Q3 divides ranked scores into four equal parts 25% 25% 25% 25% Q1 Q2 Q3 Quartiles Q1, Q2, Q3 divides ranked scores into four equal parts 25% (minimum) 25% 25% 25% Q1 Q2 Q3 (median) (maximum) Deciles D1, D2, D3, D4, D5, D6, D7, D8, D9 divides ranked data into ten equal parts Deciles D1, D2, D3, D4, D5, D6, D7, D8, D9 divides ranked data into ten equal parts 10% 10% 10% D1 D2 D3 10% 10% 10% D4 D5 D6 10% 10% 10% 10% D7 D8 D9 Percentiles 99 Percentiles Quartiles, Deciles, Percentiles Fractiles Quartiles, Deciles, Percentiles Fractiles (Quantiles) partitions data into approximately equal parts Finding the Percentile of a Given Score Finding the Percentile of a Given Score Percentile of score x = number of scores less than x • 100 total number of scores Finding the Score Given a Percentile Finding the Score Given a Percentile L= k 100 •n n total number of values in the data set k percentile being used L locator that gives the position of a value Pk kth percentile Start Finding the Value of the kth Percentile Sort the data. (Arrange the data in order of lowest to highest.) Compute k n L= 100 ( ) where n = number of values k = percentile in question Is L a whole number ? No Yes The value of the kth percentile is midway between the Lth value and the next value in the sorted set of data. Find Pk by adding the L th value and the next value and dividing the total by 2. Change L by rounding it up to the next larger whole number. The value of Pk is the Lth value, counting from the lowest Figure 2-17 Quartiles Q1 = P25 Q2 = P50 Q3 = P75 Quartiles Q1 = P25 Q2 = P50 Q3 = P75 Deciles D1 = P10 D2 = P20 D3 = P30 • • • D9 = P90 Interquartile Range (or IQR): Q3 - Q1 Interquartile Range (or IQR): Q3 - Q1 Semi-interquartile Range: Q3 - Q1 2 Interquartile Range (or IQR): Q3 - Q1 Semi-interquartile Range: Q3 - Q1 2 Midquartile: Q 1 + Q3 2 Interquartile Range (or IQR): Q3 - Q1 Semi-interquartile Range: Q3 - Q1 2 Midquartile: Q 1 + Q3 2 10 - 90 Percentile Range: P90 - P10 ELEMENTARY Section 2-7 STATISTICS Exploratory Data Analysis (EDA) MARIO F. TRIOLA EIGHTH EDITION Exploratory Data Analysis the process of using statistical tools (such as graphs, measures of center, and measures of variation) to investigate the data sets in order to understand their important characteristics Outliers a value located very far away from of the other values almost all an extreme value can have a dramatic effect on the mean, standard deviation, and on the scale of the histogram so that the true nature of the distribution is totally obscured Boxplots (Box-and-Whisker Diagram) Reveals the: center of the data spread of the data distribution of the data presence of outliers Excellent for comparing two or more data sets Boxplots 5 - number summary Minimum first quartile Q1 Median (Q2) third quartile Q3 Maximum Boxplots 2 4 6 14 0 0 Figure 2-18 2 4 6 8 10 12 14 Boxplot of Qwerty Word Ratings Figure 2-19 Boxplots Bell-Shaped Figure 2-19 Boxplots Bell-Shaped Uniform Figure 2-19 Boxplots Bell-Shaped Uniform Skewed Exploring Measures of center: mean, median, and mode Measures of variation: Standard deviation and range Measures of spread and relative location: minimum values, maximum value, and quartiles Unusual values: outliers Distribution: histograms, stem-leaf plots, and ELEMENTARY Chapter 3 MARIO F. TRIOLA STATISTICS Probability EIGHTH EDITION Chapter 3 Probability 3-1 Overview 3-2 Fundamentals 3-3 Addition Rule 3-4 Multiplication Rule: Basics 3-5 Multiplication Rule: Complements and Conditional Probability 3-6 Probabilities Through Simulations 3-7 Counting 3-1 Overview Objectives develop sound understanding of probability values used in subsequent chapters develop basic skills necessary to solve simple probability problems Rare Event Rule for Inferential Statistics: If, under a given assumption, the probability of a particular observed event is extremely small, we conclude that the assumption is probably not correct. 3-2 Fundamentals Definitions Event - any collection of results or outcomes from some procedure Simple event - any outcome or event that cannot be broken down into simpler components Sample space - all possible simple events Notation P - denotes a probability A, B, ... - denote specific events P (A) - denotes the probability of event A occurring Basic Rules for Computing Probability Rule 1: Relative Frequency Approximation Conduct (or observe) an experiment a large number of times, and count the number of times event A actually occurs, then an estimate of P(A) is Basic Rules for Computing Probability Rule 1: Relative Frequency Approximation Conduct (or observe) an experiment a large number of times, and count the number of times event A actually occurs, then an estimate of P(A) is P(A) = number of times A occurred number of times trial was repeated Basic Rules for Computing Probability Rule 2: Classical approach (requires equally likely outcomes) If a procedure has n different simple events, each with an equal chance of occurring, and s is the number of ways event A can occur, then Basic Rules for Computing Probability Rule 2: Classical approach (requires equally likely outcomes) If a procedure has n different simple events, each with an equal chance of occurring, and s is the number of ways event A can occur, then s = P(A) = n number of ways A can occur number of different simple events Basic Rules for Computing Probability Rule 3: Subjective Probabilities P(A), the probability of A, is found by simply guessing or estimating its value based on knowledge of the relevant circumstances. Rule 1 The relative frequency approach is an approximation. Rule 1 The relative frequency approach is an approximation. Rule 2 The classical approach is the actual probability. Law of Large Numbers As a procedure is repeated again and again, the relative frequency probability (from Rule 1) of an event tends to approach the actual probability. Illustration of Law of Large Numbers Figure 3-2 Example: Find the probability that a randomly selected person will be struck by lightning this year. The sample space consists of two simple events: the person is struck by lightning or is not. Because these simple events are not equally likely, we can use the relative frequency approximation (Rule 1) or subjectively estimate the probability (Rule 3). Using Rule 1, we can research past events to determine that in a recent year 377 people were struck by lightning in the US, which has a population of about 274,037,295. Therefore, P(struck by lightning in a year) 377 / 274,037,295 1/727,000 Example: On an ACT or SAT test, a typical multiple-choice question has 5 possible answers. If you make a random guess on one such question, what is the probability that your response is wrong? There are 5 possible outcomes or answers, and there are 4 ways to answer incorrectly. Random guessing implies that the outcomes in the sample space are equally likely, so we apply the classical approach (Rule 2) to get: P(wrong answer) = 4 / 5 = 0.8 Probability Limits The probability of an impossible event is 0. The probability of an event that is certain to occur is 1. Probability Limits The probability of an impossible event is 0. The probability of an event that is certain to occur is 1. 0 P(A) 1 Probability Limits The probability of an impossible event is 0. The probability of an event that is certain to occur is 1. 0 P(A) 1 Impossible to occur Probability Limits The probability of an impossible event is 0. The probability of an event that is certain to occur is 1. 0 P(A) 1 Impossible to occur Certain to occur Possible Values for Probabilities 1 Certain Likely 0.5 50-50 Chance Unlikely Figure 3-3 0 Impossible Complementary Events Complementary Events The complement of event A, denoted by A, consists of all outcomes in which event A does not occur. Complementary Events The complement of event A, denoted by A, consists of all outcomes in which event A does not occur. P(A) P(A) (read “not A”) Example: Testing Corvettes The General Motors Corporation wants to conduct a test of a new model of Corvette. A pool of 50 drivers has been recruited, 20 or whom are men. When the first person is selected from this pool, what is the probability of not getting a male driver? Example: Testing Corvettes The General Motors Corporation wants to conduct a test of a new model of Corvette. A pool of 50 drivers has been recruited, 20 or whom are men. When the first person is selected from this pool, what is the probability of not getting a male driver? Because 20 of the 50 subjects are men, it follows that 30 of the 50 subjects are women so, P(not selecting a man) = P(man) = P(woman) = 30 = 0.6 50 Rounding Off Probabilities give the exact fraction or decimal or Rounding Off Probabilities give the exact fraction or decimal or round off the final result to three significant digits Odds Odds actual odds against event A occurring are the ratio P(A) P(A), usually expressed in the form of a:b (or ‘a to b’), where a and b are integers with no common factors actual odds in favor of event A are the reciprocal of the odds against that event, b:a (or ‘b to a’) Odds The payoff odds against event A represent the ratio of net profit (if you win) to the amount of the bet. Payoff odds against event A = (net profit):(amount bet) ELEMENTARY Section 3-3 STATISTICS Addition Rule MARIO F. TRIOLA EIGHTH EDITION Definition Compound Event • Any event combining 2 or more simple events Definition Compound Event • Any event combining 2 or more simple events Notation • P(A or B) = P (event A occurs or event B occurs or they both occur) Compound Event • General Rule • When finding the probability that event A occurs or event B occurs, find the total number of ways A can occur and the number of ways B can occur, but find the total in such a way that no outcome is counted more than once. Compound Event • Formal Addition Rule • • P(A or B) = P(A) + P(B) - P(A and B) where P(A and B) denotes the probability that A and B both occur at the same time. Compound Event • Formal Addition Rule • • P(A or B) = P(A) + P(B) - P(A and B) where P(A and B) denotes the probability that A and B both occur at the same time. • Intuitive Addition Rule • To find P(A or B), find the sum of the number of ways event A can occur and the number of ways event B can occur, adding in such a way that every outcome is counted only once. P(A or B) is equal to that sum, divided by the total number of outcomes. Definition • Events A and B are mutually exclusive if they cannot occur simultaneously. Definition • Events A and B are mutually exclusive if they cannot occur simultaneously. Total Area = 1 P(A) P(B) P(A and B) Overlapping Events Figures 3-5 Definition • Events A and B are mutually exclusive if they cannot occur simultaneously. Total Area = 1 P(A) P(B) Total Area = 1 P(A) P(B) P(A and B) Overlapping Events Figures 3-5 and 3-6 Non-overlapping Events Figure 3-7 Applying the Addition Rule P(A or B) Addition Rule Are A and B mutually exclusive ? Yes No P(A or B) = P(A)+ P(B) - P(A and B) P(A or B) = P(A) + P(B) Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or a boy. Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or a boy. Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or a boy. • P(man or boy) = 1692 + 64 = 1756 = 0.790 • 2223 2223 2223 Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or a boy. • P(man or boy) = 1692 + 64 = 1756 = 0.790 • 2223 2223 2223 * Mutually Exclusive * Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or someone who survived. Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or someone who survived. Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or someone who survived. • P(man or survivor) = 1692 + 706 - 332 = 1756 • 2223 2223 2223 2223 = 0.929 Contingency Table Survived Died Total Men Women 332 318 29 27 706 1360 104 35 18 1517 1692 422 Boys 64 Girls Totals 56 2223 • Find the probability of randomly selecting a man or someone who survived. • P(man or survivor) = 1692 + 706 - 332 = 1756 • 2223 2223 2223 2223 = 0.929 * NOT Mutually Exclusive * Complementary Events Complementary Events • P(A) and P(A) • are • mutually exclusive Complementary Events • P(A) and P(A) • are • mutually exclusive • All simple events are either in A or A. Complementary Events • P(A) and P(A) • are • mutually exclusive • All simple events are either in A or A. • P(A) + P(A) = 1 Rules of Complementary Events P(A) + P(A) = 1 Rules of Complementary Events P(A) + P(A) = 1 P(A) = 1 - P(A) Rules of Complementary Events P(A) + P(A) = 1 P(A) = 1 - P(A) P(A) = 1 - P(A) Figure 3-8 Venn Diagram for the Complement of Event A Total Area = 1 P (A) P (A) = 1 - P (A) ELEMENTARY Section 3-4 STATISTICS Multiplication Rule: Basics MARIO F. TRIOLA EIGHTH EDITIO Finding the Probability of Two or More Selections Multiple selections Multiplication Rule Notation P(A and B) = P(event A occurs in a first trial and event B occurs in a second trial) FIGURE 3-9 Tree Diagram of Test Answers FIGURE 3-9 Tree Diagram of Test Answers T F a b c d e a b c d e Ta Tb Tc Td Te Fa Fb Fc Fd Fe FIGURE 3-9 Tree Diagram of Test Answers T F a b c d e a b c d e Ta Tb Tc Td Te Fa Fb Fc Fd Fe FIGURE 3-9 Tree Diagram of Test Answers T F P(T) = 1 2 a b c d e a b c d e Ta Tb Tc Td Te Fa Fb Fc Fd Fe FIGURE 3-9 Tree Diagram of Test Answers a b c d T P(T) = F e a b 1 2 c d e 1 5 P(c) = Ta Tb Tc Td Te Fa Fb Fc Fd Fe FIGURE 3-9 Tree Diagram of Test Answers a b c d T P(T) = F e a b 1 2 c d e 1 5 P(c) = Ta Tb Tc Td Te Fa Fb Fc Fd Fe P(T and c) = 1 10 P (both correct) P (both correct) = P (T and c) P (both correct) = P (T and c) 1 10 1 2 1 5 P (both correct) = P (T and c) 1 = 10 1 1 • 2 5 Multiplication Rule P (both correct) = P (T and c) 1 = 10 1 1 • 2 5 Multiplication Rule INDEPENDENT EVENTS Notation for Conditional Probability P(B A) represents the probability of event B occurring after it is assumed that event A has already occurred (read B A as “B given A”). Definitions Independent Events Two events A and B are independent if the occurrence of one does not affect the probability of the occurrence of the other. Dependent Events If A and B are not independent, they are said to be dependent. Formal Multiplication Rule P(A and B) = P(A) • P(B A) If A and B are independent events, P(B A) is really the same as P(B) Figure 3-10 Applying the Multiplication Rule P(A or B) Multiplication Rule Are A and B independent ? Yes No P(A and B) = P(A) • P(B A) P(A and B) = P(A) • P(B) Intuitive Multiplication When finding the probability that event A occurs in one trial and B occurs in the next trial, multiply the probability of event A by the probability of event B, but be sure that the probability of event B takes into account the previous occurrence of event A. Small Samples from Large Populations If a sample size is no more than 5% of the size of the population, treat the selections as being independent (even if the selections are made without replacement, so they are technically dependent). ELEMENTARY Section 3-5 STATISTICS Multiplication Rule: Complements and Conditional Probability MARIO F. TRIOLA EIGHTH EDITION Probability of ‘At Least One’ Probability of ‘At Least One’ ‘At least one’ is equivalent to ‘one or more’. Probability of ‘At Least One’ ‘At least one’ is equivalent to ‘one or more’. The complement of getting at least one item of a particular type is that you get no items of that type. Probability of ‘At Least One’ ‘At least one’ is equivalent to ‘one or more’. The complement of getting at least one item of a particular type is that you get no items of that type. If P(A) = P(getting at least one), then Probability of ‘At Least One’ ‘At least one’ is equivalent to ‘one or more’. The complement of getting at least one item of a particular type is that you get no items of that type. If P(A) = P(getting at least one), then P(A) = 1 - P(A) Probability of ‘At Least One’ ‘At least one’ is equivalent to ‘one or more’. The complement of getting at least one item of a particular type is that you get no items of that type. If P(A) = P(getting at least one), then P(A) = 1 - P(A) where P(A) is P(getting none) Probability of ‘At Least One’ Find the probablility of a couple have at least 1 girl among 3 children. Probability of ‘At Least One’ Find the probablility of a couple have at least 1 girl among 3 children. If P(A) = P(getting at least 1 girl), then P(A) = 1 - P(A) where P(A) is P(getting no girls) Probability of ‘At Least One’ Find the probablility of a couple have at least 1 girl among 3 children. If P(A) = P(getting at least 1 girl), then P(A) = 1 - P(A) where P(A) is P(getting no girls) P(A) = (0.5)(0.5)(0.5) = 0.125 Probability of ‘At Least One’ Find the probablility of a couple have at least 1 girl among 3 children. If P(A) = P(getting at least 1 girl), then P(A) = 1 - P(A) where P(A) is P(getting no girls) P(A) = (0.5)(0.5)(0.5) = 0.125 P(A) = 1 - 0.125 = 0.875 Conditional Probability Definition The conditional probability of event B occurring, given that A has already occurred, can be found by dividing the probability of events A and B both occurring by the probability of event A. Conditional Probability P(A and B) = P(A) • P(B|A) Conditional Probability P(A and B) = P(A) • P(B|A) Formal Conditional Probability P(A and B) = P(A) • P(B|A) Formal P(B|A) = P(A and B) P(A) Conditional Probability P(A and B) = P(A) • P(B|A) Formal P(B|A) = Intuitive P(A and B) P(A) Conditional Probability P(A and B) = P(A) • P(B|A) Formal P(B|A) = Intuitive P(A and B) P(A) The conditional probability of B given A can be found by assuming the event A has occurred and, operating under that assumption, calculating the probability that event B will occur. Testing for Independence Testing for Independence If P(B|A) = P(B) then the occurrence of A has no effect on the probability of event B; that is, A and B are independent events. Testing for Independence If P(B|A) = P(B) then the occurrence of A has no effect on the probability of event B; that is, A and B are independent events. or If P(A and B) = P(A) • P(B) then A and B are independent events. ELEMENTARY STATISTICS Chapter 4 Probability Distributions MARIO F. TRIOLA EIGHTH EDITION Chapter 4 Probability Distributions 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, Standard Deviation for the Binomial Distribution 4-5 The Poisson Distribution 4-1 Overview This chapter will deal with the construction of probability distributions by combining the methods of Chapter 2 with the those of Chapter 3. Probability Distributions will describe what will probably happen instead of what actually did happen. Combining Descriptive Statistics Methods and Probabilities to Form a Theoretical Model of Behavior Figure 4-1 4-2 Random Variables Definitions Random Variable a variable (typically represented by x) that has a single numerical value, determined by chance, for each outcome of a procedure Probability Distribution a graph, table, or formula that gives the probability for each value of the random variable Table 4-1 Probability Distribution Number of Girls Among Fourteen Newborn Babies x P(x) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0.000 0.001 0.006 0.022 0.061 0.122 0.183 0.209 0.183 0.122 0.061 0.022 0.006 0.001 0.000 Definitions Discrete random variable has either a finite number of values or countable number of values, where ‘countable’ refers to the fact that there might be infinitely many values, but they result from a counting process. Continuous random variable has infinitely many values, and those values can be associated with measurements on a continuous scale with no gaps or interruptions. Probability Histogram Figure 4-3 Requirements for Probability Distribution Requirements for Probability Distribution P(x) = 1 where x assumes all possible values Requirements for Probability Distribution P(x) = 1 where x assumes all possible values 0 P(x) 1 for every value of x Mean, Variance and Standard Deviation of a Probability Distribution Formula 4-1 µ = [x • P(x)] Formula 4-2 2 2 s = [(x - µ) • P(x)] Formula 4-3 2 2 2 s = [ x • P(x)] - µ (shortcut) Mean, Variance and Standard Deviation of a Probability Distribution Formula 4-1 µ = [x • P(x)] Formula 4-2 2 2 s = [(x - µ) • P(x)] Formula 4-3 2 2 2 s = [ x • P(x)] - µ (shortcut) Formula 4-4 s = [ x 2 • P(x)] - µ 2 Mean, Variance and Standard Deviation of a Probability Distribution Formula 4-1 µ = [x • P(x)] Formula 4-2 2 2 s = [(x - µ) • P(x)] Formula 4-3 2 2 2 s = [ x • P(x)] - µ (shortcut) Formula 4-4 s = [ x 2 • P(x)] - µ 2 Roundoff Rule for µ, s , and s 2 Round results by carrying one more decimal place than the number of decimal places used for the random variable x. If the values of x are integers, round µ, s2, and s to one decimal place. Definition Expected Value The average value of outcomes E = [x • P(x)] E = [x • P(x)] Event Win Lose E = [x • P(x)] Event x Win $499 Lose - $1 E = [x • P(x)] Event x P(x) Win $499 0.001 Lose - $1 0.999 E = [x • P(x)] Event x P(x) x • P(x) Win $499 0.001 0.499 Lose - $1 0.999 - 0.999 E = [x • P(x)] Event x P(x) x • P(x) Win $499 0.001 0.499 Lose - $1 0.999 - 0.999 E = -$.50 ELEMENTARY Section 4-3 STATISTICS Binomial Probability Distributions MARIO F. TRIOLA EIGHTH EDITION Definitions Binomial Probability Distribution 1. The experiment must have a fixed number of trials. 2. The trials must be independent. (The outcome of any individual trial doesn’t affect the probabilities in the other trials.) 3. Each trial must have all outcomes classified into two categories. 4. The probabilities must remain constant for each trial. Notation for Binomial Probability Distributions n = fixed number of trials x = specific number of successes in n trials p = probability of success in one of n trials q = probability of failure in one of n trials (q = 1 - p ) P(x) = probability of getting exactly x success among n trials Be sure that x and p both refer to the same category being called a success. Method 1 Binomial Probability Formula Method 1 Binomial Probability Formula P(x) = n! • (n - x )! x! px • n-x q Method 1 Binomial Probability Formula P(x) = n! • (n - x )! x! P(x) = nCx • px px • • n-x q qn-x for calculators with nCr key, where r = x Example: Find the probability of getting exactly 3 correct responses among 5 different requests from AT&T directory assistance. Assume in general, AT&T is correct 90% of the time. This is a binomial experiment where: n=5 x=3 p = 0.90 q = 0.10 Example: Find the probability of getting exactly 3 correct responses among 5 different requests from AT&T directory assistance. Assume in general, AT&T is correct 90% of the time. This is a binomial experiment where: n=5 x=3 p = 0.90 q = 0.10 Using the binomial probability formula to solve: P(3) = 5C3 3 2 • 0.9 • 01 = 0.0.0729 Method 2 Table A-1 in Appendix A For n = 15 and p = 0.10 Table A-1 n x P(x) 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.206 0.343 0.267 0.129 0.043 0.010 0.002 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ For n = 15 and p = 0.10 Table A-1 n x P(x) 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.206 0.343 0.267 0.129 0.043 0.010 0.002 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ For n = 15 and p = 0.10 Table A-1 Binomial Probability Distribution n x P(x) x P(x) 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.206 0.343 0.267 0.129 0.043 0.010 0.002 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0.0+ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0.206 0.343 0.267 0.129 0.043 0.010 0.002 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 Example: Using Table A-1 for n = 5 and p = 0.90, find the following: a) The probability of exactly 3 successes b) The probability of at least 3 successes a) P(3) = 0.073 b) P(at least 3) = P(3 or 4 or 5) = P(3) or P(4) or P(5) = 0.073 + 0.328 + 0.590 = 0.991 Method 3 Using Technology STATDISK Minitab Excel TI-83 Plus Binomial Probability Formula P(x) = n! • (n - x )! x! Number of outcomes with exactly x successes among n trials px • n-x q Binomial Probability Formula P(x) = n! • (n - x )! x! Number of outcomes with exactly x successes among n trials px • n-x q Probability of x successes among n trials for any one particular order ELEMENTARY Section 4-4 STATISTICS Mean, Variance, and Standard Deviation for the Binomial Distribution MARIO F. TRIOLA EIGHTH EDITION For Any Discrete Probability Distribution: • Formula 4-1 µ = [x • P(x)] • Formula 4-3 s 2 = [ x • P(x) ] - µ 2 2 For Any Discrete Probability Distribution: • Formula 4-1 µ = [x • P(x)] • Formula 4-3 s 2 Formula 4-4 s = = [ x • P(x) ] - µ 2 [ x • P(x) ] - µ 2 2 2 For Binomial Distributions: • Formula 4-6 µ =n•p • Formula 4-7 s = n • p • q 2 For Binomial Distributions: • Formula 4-6 µ =n•p • Formula 4-7 s = n • p • q 2 Formula 4-8 s= n • p • q Example: Find the mean and standard deviation for the number of girls in groups of 14 births. • We previously discovered that this scenario could be considered a binomial experiment where: • n = 14 • p = 0.5 • q = 0.5 • Using the binomial distribution formulas: Example: Find the mean and standard deviation for the number of girls in groups of 14 births. • We previously discovered that this scenario could be considered a binomial experiment where: • n = 14 • p = 0.5 • q = 0.5 • Using the binomial distribution formulas: • µ = (14)(0.5) = 7 girls s= (14)(0.5)(0.5) = 1.9 girls (rounded) Reminder • Maximum usual values = µ + 2 s • Minimum usual values = µ - 2 s Example: Determine whether 68 girls among 100 babies could easily occur by chance. • For this binomial distribution, • µ = 50 girls s= 5 girls • µ + 2 s = 50 + 2(5) = 60 • µ - 2 s = 50 - 2(5) = 40 • The usual number girls among 100 births would be from 40 to 60. So 68 girls in 100 births is an unusual result. ELEMENTARY Chapter 5 STATISTICS Normal Probability Distributions MARIO F. TRIOLA EIGHTH EDITION Chapter 5 Normal Probability Distributions 5-1 Overview 5-2 The Standard Normal Distribution 5-3 Normal Distributions: Finding Probabilities 5-4 Normal Distributions: Finding Values 5-5 The Central Limit Theorem 5-6 Normal Distribution as Approximation to Binomial Distribution 5-7 Determining Normality 5-1 Overview Continuous random variable Normal distribution 5-1 Overview Continuous random variable Normal distribution Curve is bell shaped and symmetric Figure 5-1 µ Score 5-1 Overview Continuous random variable Normal distribution Curve is bell shaped and symmetric Figure 5-1 µ Score Formula 5-1 y= e 1 2 s ( x - µ) s 2 2 5-2 The Standard Normal Distribution Definitions Uniform Distribution a probability distribution in which the continuous random variable values are spread evenly over the range of possibilities; the graph results in a rectangular shape. Definitions Density Curve (or probability density function) the graph of a continuous probability distribution Definitions Density Curve (or probability density function) the graph of a continuous probability distribution 1. The total area under the curve must equal 1. 2. Every point on the curve must have a vertical height that is 0 or greater. Because the total area under the density curve is equal to 1, there is a correspondence between area and probability. Times in First or Last Half Hours Figure 5-3 Heights of Adult Men and Women Women: µ = 63.6 s = 2.5 Figure 5-4 Men: µ = 69.0 s = 2.8 63.6 69.0 Height (inches) Definition Standard Normal Deviation a normal probability distribution that has a mean of 0 and a standard deviation of 1 Definition Standard Normal Deviation a normal probability distribution that has a mean of 0 and a standard deviation of 1 Area found in Table A-2 Area = 0.3413 0.4429 -3 -2 -1 0 1 2 3 0 z = 1.58 Score (z ) Figure 5-5 Figure 5-6 Table A-2 Back left cover of text book Formulas and Tables card Appendix Table A-2 Standard Normal Distribution s=1 µ=0 0 x z Table A-2 Standard Normal (z) Distribution z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 .0000 .0398 .0793 .1179 .1554 .1915 .2257 .2580 .2881 .3159 .3413 .3643 .3849 .4032 .4192 .4332 .4452 .4554 .4641 .4713 .4772 .4821 .4861 .4893 .4918 .4938 .4953 .4965 .4974 .4981 .4987 .0040 .0438 .0832 .1217 .1591 .1950 .2291 .2611 .2910 .3186 .3438 .3665 .3869 .4049 .4207 .4345 .4463 .4564 .4649 .4719 .4778 .4826 .4864 .4896 .4920 .4940 .4955 .4966 .4975 .4982 .4987 .0080 .0478 .0871 .1255 .1628 .1985 .2324 .2642 .2939 .3212 .3461 .3686 .3888 .4066 .4222 .4357 .4474 .4573 .4656 .4726 .4783 .4830 .4868 .4898 .4922 .4941 .4956 .4967 .4976 .4982 .4987 .0120 .0517 .0910 .1293 .1664 .2019 .2357 .2673 .2967 .3238 .3485 .3708 .3907 .4082 .4236 .4370 .4484 .4582 .4664 .4732 .4788 .4834 .4871 .4901 .4925 .4943 .4957 .4968 .4977 .4983 .4988 .0160 .0557 .0948 .1331 .1700 .2054 .2389 .2704 .2995 .3264 .3508 .3729 .3925 .4099 .4251 .4382 .4495 .4591 .4671 .4738 .4793 .4838 .4875 .4904 .4927 .4945 .4959 .4969 .4977 .4984 .4988 .0199 .0596 .0987 .1368 .1736 .2088 .2422 .2734 .3023 .3289 .3531 .3749 .3944 .4115 .4265 .4394 .4505 .4599 .4678 .4744 .4798 .4842 .4878 .4906 .4929 .4946 .4960 .4970 .4978 .4984 .4989 .0239 .0636 .1026 .1406 .1772 .2123 .2454 .2764 .3051 .3315 .3554 .3770 .3962 .4131 .4279 .4406 .4515 .4608 .4686 .4750 .4803 .4846 .4881 .4909 .4931 .4948 .4961 .4971 .4979 .4985 .4989 .0279 .0675 .1064 .1443 .1808 .2157 .2486 .2794 .3078 .3340 .3577 .3790 .3980 .4147 .4292 .4418 .4525 .4616 .4693 .4756 .4808 .4850 .4884 .4911 .4932 .4949 .4962 .4972 .4979 .4985 .4989 .0319 .0714 .1103 .1480 .1844 .2190 .2517 .2823 .3106 .3365 .3599 .3810 .3997 .4162 .4306 .4429 .4535 .4625 .4699 .4761 .4812 .4854 .4887 .4913 .4934 .4951 .4963 .4973 .4980 .4986 .4990 .0359 .0753 .1141 .1517 .1879 .2224 .2549 .2852 .3133 .3389 .3621 .3830 .4015 .4177 .4319 .4441 .4545 .4633 .4706 .4767 .4817 .4857 .4890 .4916 .4936 .4952 .4964 .4974 .4981 .4986 .4990 * * To find: z Score the distance along horizontal scale of the standard normal distribution; refer to the leftmost column and top row of Table A-2 Area the region under the curve; refer to the values in the body of Table A-2 Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1.58 degrees. Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1.58 degrees. P ( 0 < x < 1.58 ) = 0 1.58 Table A-2 Standard Normal (z) Distribution z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 .0000 .0398 .0793 .1179 .1554 .1915 .2257 .2580 .2881 .3159 .3413 .3643 .3849 .4032 .4192 .4332 .4452 .4554 .4641 .4713 .4772 .4821 .4861 .4893 .4918 .4938 .4953 .4965 .4974 .4981 .4987 .0040 .0438 .0832 .1217 .1591 .1950 .2291 .2611 .2910 .3186 .3438 .3665 .3869 .4049 .4207 .4345 .4463 .4564 .4649 .4719 .4778 .4826 .4864 .4896 .4920 .4940 .4955 .4966 .4975 .4982 .4987 .0080 .0478 .0871 .1255 .1628 .1985 .2324 .2642 .2939 .3212 .3461 .3686 .3888 .4066 .4222 .4357 .4474 .4573 .4656 .4726 .4783 .4830 .4868 .4898 .4922 .4941 .4956 .4967 .4976 .4982 .4987 .0120 .0517 .0910 .1293 .1664 .2019 .2357 .2673 .2967 .3238 .3485 .3708 .3907 .4082 .4236 .4370 .4484 .4582 .4664 .4732 .4788 .4834 .4871 .4901 .4925 .4943 .4957 .4968 .4977 .4983 .4988 .0160 .0557 .0948 .1331 .1700 .2054 .2389 .2704 .2995 .3264 .3508 .3729 .3925 .4099 .4251 .4382 .4495 .4591 .4671 .4738 .4793 .4838 .4875 .4904 .4927 .4945 .4959 .4969 .4977 .4984 .4988 .0199 .0596 .0987 .1368 .1736 .2088 .2422 .2734 .3023 .3289 .3531 .3749 .3944 .4115 .4265 .4394 .4505 .4599 .4678 .4744 .4798 .4842 .4878 .4906 .4929 .4946 .4960 .4970 .4978 .4984 .4989 .0239 .0636 .1026 .1406 .1772 .2123 .2454 .2764 .3051 .3315 .3554 .3770 .3962 .4131 .4279 .4406 .4515 .4608 .4686 .4750 .4803 .4846 .4881 .4909 .4931 .4948 .4961 .4971 .4979 .4985 .4989 .0279 .0675 .1064 .1443 .1808 .2157 .2486 .2794 .3078 .3340 .3577 .3790 .3980 .4147 .4292 .4418 .4525 .4616 .4693 .4756 .4808 .4850 .4884 .4911 .4932 .4949 .4962 .4972 .4979 .4985 .4989 .0319 .0714 .1103 .1480 .1844 .2190 .2517 .2823 .3106 .3365 .3599 .3810 .3997 .4162 .4306 .4429 .4535 .4625 .4699 .4761 .4812 .4854 .4887 .4913 .4934 .4951 .4963 .4973 .4980 .4986 .4990 .0359 .0753 .1141 .1517 .1879 .2224 .2549 .2852 .3133 .3389 .3621 .3830 .4015 .4177 .4319 .4441 .4545 .4633 .4706 .4767 .4817 .4857 .4890 .4916 .4936 .4952 .4964 .4974 .4981 .4986 .4990 * * Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1.58 degrees. Area = 0.4429 P ( 0 < x < 1.58 ) = 0.4429 0 1.58 Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1.58 degrees. Area = 0.4429 P ( 0 < x < 1.58 ) = 0.4429 0 1.58 The probability that the chosen thermometer will measure freezing water between 0 and 1.58 degrees is 0.4429. Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1.58 degrees. Area = 0.4429 P ( 0 < x < 1.58 ) = 0.4429 0 1.58 There is 44.29% of the thermometers with readings between 0 and 1.58 degrees. Using Symmetry to Find the Area to the Left of the Mean Because of symmetry, these areas are equal. Figure 5-7 (a) (b) 0.4925 0.4925 0 z = - 2.43 0 Equal distance away from 0 z = 2.43 NOTE: Although a z score can be negative, the area under the curve (or the corresponding probability) can never be negative. Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water, and if one thermometer is randomly selected, find the probability that it reads freezing water between -2.43 degrees and 0 degrees. Area = 0.4925 P ( -2.43 < x < 0 ) = 0.4925 -2.43 0 The probability that the chosen thermometer will measure freezing water between -2.43 and 0 degrees is 0.4925. The Empirical Rule Standard Normal Distribution: µ = 0 and s = 1 The Empirical Rule Standard Normal Distribution: µ = 0 and s = 1 68% within 1 standard deviation 34% x-s 34% x x+s The Empirical Rule Standard Normal Distribution: µ = 0 and s = 1 95% within 2 standard deviations 68% within 1 standard deviation 34% 34% 13.5% x - 2s 13.5% x-s x x+s x + 2s The Empirical Rule Standard Normal Distribution: µ = 0 and s = 1 99.7% of data are within 3 standard deviations of the mean 95% within 2 standard deviations 68% within 1 standard deviation 34% 34% 2.4% 2.4% 0.1% 0.1% 13.5% x - 3s x - 2s 13.5% x-s x x+s x + 2s x + 3s Probability of Half of a Distribution 0.5 0 Finding the Area to the Right of z = 1.27 Value found in Table A-2 0.3980 0 Figure 5-8 This area is 0.5 - 0.3980 = 0.1020 z = 1.27 Finding the Area Between z = 1.20 and z = 2.30 0.4893 (from Table A-2 with z = 2.30) Area A is 0.4893 - 0.3849 = 0.1044 0.3849 A 0 Figure 5-9 z = 1.20 z = 2.30 Notation P(a < z < b) denotes the probability that the z score is between a and b P(z > a) denotes the probability that the z score is greater than a P (z < a) denotes the probability that the z score is less than a Figure 5-10 Interpreting Area Correctly Interpreting Area Correctly Figure 5-10 ‘greater than ‘at least x’ x’ ‘more than Subtract from 0.5 Add to 0.5 x’ ‘not less than x’ 0.5 x x Interpreting Area Correctly Figure 5-10 ‘greater than ‘at least x’ Add to 0.5 x’ ‘more than Subtract from 0.5 x’ ‘not less than x’ 0.5 x Add to 0.5 x ‘less than ‘at most x’ x’ ‘no more than x’ ‘not greater than Subtract from 0.5 x’ 0.5 x x Interpreting Area Correctly Figure 5-10 ‘greater than ‘at least x’ Add to 0.5 x’ ‘more than Subtract from 0.5 x’ ‘not less than x’ 0.5 x Add to 0.5 x ‘less than ‘at most x’ x’ ‘no more than x’ ‘not greater than Subtract from 0.5 x’ 0.5 x x Add C ‘between x1 and Use A=C-B x2’ A x1 x2 x1 x2 B Finding a z - score when given a probability Using Table A-2 1. Draw a bell-shaped curve, draw the centerline, and identify the region under the curve that corresponds to the given probability. If that region is not bounded by the centerline, work with a known region that is bounded by the centerline. 2. Using the probability representing the area bounded by the centerline, locate the closest probability in the body of Table A-2 and identify the corresponding z score. 3. If the z score is positioned to the left of the centerline, make it a negative. Finding z Scores when Given Probabilities 95% 5% 5% or 0.05 0.45 0.50 z 0 ( z score will be positive ) FIGURE 5-11 Finding the 95th Percentile Finding z Scores when Given Probabilities 95% 5% 5% or 0.05 0.45 0.50 0 1.645 (z score will be positive) FIGURE 5-11 Finding the 95th Percentile Finding z Scores when Given Probabilities 90% 10% Bottom 10% 0.10 0.40 z 0 (z score will be negative) FIGURE 5-12 Finding the 10th Percentile Finding z Scores when Given Probabilities 90% 10% Bottom 10% 0.10 0.40 -1.28 0 (z score will be negative) FIGURE 5-12 Finding the 10th Percentile ELEMENTARY Section 5-3 STATISTICS Normal Distributions: Finding Probabilities MARIO F. TRIOLA EIGHTH EDITION Other Normal Distributions m s If 0 or 1 (or both), we will convert values to standard scores using Formula 5-2, then procedures for working with all normal distributions are the same as those for the standard normal distribution. Other Normal Distributions m s If 0 or 1 (or both), we will convert values to standard scores using Formula 5-2, then procedures for working with all normal distributions are the same as those for the standard normal distribution. Formula 5-2 z= x-µ s Converting to Standard Normal Distribution P (a) Figure 5-13 m x Converting to Standard Normal Distribution x-m z= s P P (a) Figure 5-13 m x (b) 0 z Probability of Weight between 143 pounds and 201 pounds z= x = 143 s = 29 143 Figure 5-14 0 201 2.00 201 - 143 29 = 2.00 Weight z Probability of Weight between 143 pounds and 201 pounds Value found in Table A-2 x = 143 s = 29 143 Figure 5-14 0 201 2.00 Weight z Probability of Weight between 143 pounds and 201 pounds 0.4772 x = 143 s = 29 143 Figure 5-14 0 201 2.00 Weight z Probability of Weight between 143 pounds and 201 pounds There is a 0.4772 probability of randomly selecting a woman with a weight between 143 and 201 lbs. x = 143 s = 29 143 Figure 5-14 0 201 2.00 Weight z Probability of Weight between 143 pounds and 201 pounds OR - 47.72% of women have weights between 143 lb and 201 lb. x = 143 s = 29 143 Figure 5-14 0 201 2.00 Weight z ELEMENTARY Section 5-4 STATISTICS Normal Distributions: Finding Values MARIO F. TRIOLA EIGHTH EDITION Cautions to keep in mind 1. Don’t confuse z scores and areas. Z scores are distances along the horizontal scale, but areas are regions under the normal curve. Table A-2 lists z scores in the left column and across the top row, but areas are found in the body of the table. 2. Choose the correct (right/left) side of the graph. 3. A z score must be negative whenever it is located to the left of the centerline of 0. Finding z Scores when Given Probabilities 95% 5% 5% or 0.05 0.45 0.50 0 1.645 (z score will be positive) FIGURE 5-11 Finding the 95th Percentile Finding z Scores when Given Probabilities 90% 10% Bottom 10% 0.10 0.40 -1.28 0 (z score will be negative) FIGURE 5-12 Finding the 10th Percentile Procedure for Finding Values Using Table A-2 and Formula 5-2 1. Sketch a normal distribution curve, enter the given probability or percentage in the appropriate region of the graph, and identify the value(s) being sought. x 2. Use Table A-2 to find the z score corresponding to the region bounded by x and the centerline of 0. Cautions: Refer to the BODY of Table A-2 to find the closest area, then identify the corresponding z score. Make the z score negative if it is located to the left of the centerline. 3. Using Formula 5-2, enter the values for µ, s, and the z score found in step 2, then solve for x. x = µ + (z • s) (Another form of Formula 5-2) 4. Refer to the sketch of the curve to verify that the solution makes sense in the context of the graph and the context of the problem. Finding P10 for Weights of Women 10% 90% 40% x=? FIGURE 5-17 143 50% Weight Finding P10 for Weights of Women 0.10 0.40 FIGURE 5-17 0.50 x=? 143 -1.28 0 Weight Finding P10 for Weights of Women x = 143 + (-1.28 • 29) = 105.88 0.10 0.40 FIGURE 5-17 0.50 x=? 143 -1.28 0 Weight Finding P10 for Weights of Women The weight of 106 lb (rounded) separates the lowest 10% from the highest 90%. 0.10 0.40 x = 106 FIGURE 5-17 -1.28 0.50 143 0 Weight Forgot to make z score negative??? x = 143 + (1.28 • 29) = 180 0.10 0.40 FIGURE 5-17 0.50 x=? 143 1.28 0 Weight Forgot to make z score negative??? x = 143 + (1.28 • 29) = 180 0.10 0.40 x = 180 FIGURE 5-17 1.28 0.50 143 0 Weight Forgot to make z score negative??? UNREASONABLE ANSWER! 0.10 0.40 x = 180 FIGURE 5-17 1.28 0.50 143 0 Weight REMEMBER! Make the z score negative if the value is located to the left (below) the mean. Otherwise, the z score will be positive. ELEMENTARY Section 5-5 S TATISTICS The Central Limit Theorem MARIO F. TRIOLA EIGHTH EDITION Definition Sampling Distribution of the mean the probability distribution of sample means, with all samples having the same sample size n. Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation s. 2. Samples all of the same size n are randomly selected from the population of x values. Central Limit Theorem Conclusions: Central Limit Theorem Conclusions: 1. The distribution of sample x will, as the sample size increases, approach a normal distribution. Central Limit Theorem Conclusions: 1. The distribution of sample x will, as the sample size increases, approach a normal distribution. 2. The mean of the sample means will be the population mean µ. Central Limit Theorem Conclusions: 1. The distribution of sample x will, as the sample size increases, approach a normal distribution. 2. The mean of the sample means will be the population mean µ. 3. The standard deviation of the sample means will approach s n Practical Rules Commonly Used: 1. For samples of size n larger than 30, the distribution of the sample means can be approximated reasonably well by a normal distribution. The approximation gets better as the sample size n becomes larger. 2. If the original population is itself normally distributed, then the sample means will be normally distributed for any sample size n (not just the values of n larger than 30). Notation Notation the mean of the sample means µx = µ Notation the mean of the sample means µx = µ the standard deviation of sample mean s sx = n Notation the mean of the sample means µx = µ the standard deviation of sample mean s sx = n (often called standard error of the mean) Distribution of 200 digits from Social Security Numbers Frequency (Last 4 digits from 50 students) 20 10 0 0 1 2 3 4 5 6 7 Distribution of 200 digits Figure 5-19 8 9 Table 5-2 x SSN digits 1 5 9 5 9 4 7 9 5 7 2 6 2 2 5 0 2 7 8 5 8 3 8 1 3 2 7 1 3 3 7 7 3 4 4 4 5 1 3 6 6 3 8 2 3 6 1 5 3 4 6 7 3 7 3 3 8 3 7 6 4 6 8 5 5 2 6 4 9 4.75 4.25 8.25 3.25 5.00 3.50 5.25 4.75 5.00 2 6 1 9 5 7 8 6 4 0 7 4.00 5.25 4.25 4.50 4.75 3.75 5.25 3.75 4.50 6.00 Frequency Distribution of 50 Sample Means for 50 Students 15 10 5 0 0 Figure 5-20 1 2 3 4 5 6 7 8 9 As the sample size increases, the sampling distribution of sample means approaches a normal distribution. Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. b.) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. z = 150-143 = 0.24 29 0.5 - 0.0948 = 0.4052 0.0948 m = 143 s= 29 0 150 0.24 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, the probability that her weight is greater than 150 lb. is 0.4052. 0.5 - 0.0948 = 0.4052 0.0948 m = 143 s= 29 0 150 0.24 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, b.) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, b.) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. mx = 143 150 sx = 29 = 4.83333 36 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, b.) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. z = 150-143 = 1.45 29 36 0.4265 mx = 143 sx = 4.83333 0 150 1.45 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, b.) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. z = 150-143 = 1.45 29 36 0.5 - 0.4265 = 0.0735 0.4265 mx = 143 sx = 4.83333 0 150 1.45 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, b.) if 36 different women are randomly selected, the probability that their mean weight is greater than 150 lb is 0.0735. z = 150-143 = 1.45 29 36 0.5 - 0.4265 = 0.0735 0.4265 mx = 143 sx = 4.83333 0 150 1.45 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. P(x > 150) = 0.4052 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. P(x > 150) = 0.4052 b.) if 36 different women are randomly selected, their mean weight is greater than 150 lb. P(x > 150) = 0.0735 Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a.) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. P(x > 150) = 0.4052 b.) if 36 different women are randomly selected, their mean weight is greater than 150 lb. P(x > 150) = 0.0735 It is much easier for an individual to deviate from the mean than it is for a group of 36 to deviate from the mean. Sampling Without Replacement If n > 0.05 N Sampling Without Replacement If n > 0.05 N sx = s n N-n N-1 Sampling Without Replacement If n > 0.05 N sx = s n N-n N-1 finite population correction factor ELEMENTARY Section 5-6 STATISTICS Normal Distribution as Approximation to Binomial Distribution MARIO F. TRIOLA EIGHTH EDITION Review Binomial Probability Distribution 1. The procedure must have fixed number of trials. 2. The trials must be independent. 3. Each trial must have all outcomes classified into two categories. 4. The probabilities must remain constant for each trial. Solve by binomial probability formula, Table A-1, or technology Approximate a Binomial Distribution with a Normal Distribution if: np 5 nq 5 Approximate a Binomial Distribution with a Normal Distribution if: np 5 nq 5 then µ = np and s = npq and the random variable has a distribution. (normal) Solving Binomial Probability Problems Using a Normal Approximation Figure 5-24 Solving Binomial Probability Problems Using a Normal Approximation Figure 5-24 Start 1 2 3 4 First try to solve the binomial probability problem by using 1. Software or a calculator 2. Table A-1 3. The binomial probability formula Are np 5 and nq 5 both true ? No Use binomial probability formula P(x) = n! • px • qn-x (n - x)!x! Yes Compute µ = np and s = npq Draw the normal curve, and identify the region representing the probability to be found. Be sure to include the continuity correction. (Remember, the discrete value x is adjusted for continuity by adding and subtracting 0.5) Solving Binomial Probability Problems Using a Normal Approximation Figure 5-24 Draw the normal curve, and identify the region representing the probability to be found. Be sure to include the continuity correction. (Remember, the discrete value x is adjusted for continuity by adding and subtracting 0.5) 4 5 6 Use Table A-2 for the standard normal distribution Calculate z x m s where µ and sare the values already found and x has been adjusted for continuity Refer to Table A-2 to find the area between µ and the value of x adjusted for continuity. Use that area to find the probability being sought. Use a TI-83 calculator Press 2nd, VARS, 2 (for normalcdf), enter (lower score, upper, µ, s). Procedure for Using a Normal Distribution to Approximate a Binomial Distribution 1. Establish that the normal distribution is a suitable approximation to the binomial distribution by verifying np 5 and nq 5. 2. Find the values of the parameters µ and s by calculating µ = np and s = npq. 3. Identify the discrete value of x (the number of successes). Change the discrete value x by replacing it with the interval from x - 0.5 to x + 0.5. Draw a normal curve and enter the values of µ , s, and either x - 0.5 or x + 0.5, as appropriate. continued Procedure for Using a Normal Distribution to Approximate a Binomial Distribution continued 4. Change x by replacing it with x - 0.5 or x + 0.5, as appropriate. 5. Find the area corresponding to the desired probability. Finding the Probability of “At Least” 520 Men Among 1000 Accepted Applicants Figure 5-25 Definition When we use the normal distribution (which is continuous) as an approximation to the binomial distribution (which is discrete), a continuity correction is made to a discrete whole number x in the binomial distribution by representing the single value x by the interval from x - 0.5 to x + 0.5. Procedure for Continuity Corrections 1. When using the normal distribution as an approximation to the binomial distribution, always use the continuity correction. 2. In using the continuity correction, first identify the discrete whole number x that is relevant to the binomial probability problem. 3. Draw a normal distribution centered about µ, then draw a vertical strip area centered over x . Mark the left side of the strip with the number x - 0.5, and mark the right side with x + 0.5. For x =520, draw a strip from 519.5 to 520.5. Consider the area of the strip to represent the probability of discrete number x. continued Procedure for Continuity Corrections continued 4. Now determine whether the value of x itself should be included in the probability you want. Next, determine whether you want the probability of at least x, at most x, more than x, fewer than x, or exactly x. Shade the area to the right or left of the strip, as appropriate; also shade the interior of the strip itself if and only if itself is to be included. The total shaded region corresponds to probability being sought. x x = at least 520 = 520, 521, 522, . . . . 520 519.5 Figure 5-26 x = at least 520 = 520, 521, 522, . . . . 520 519.5 x = more than 520 = 521, 522, 523, . . . 521 520.5 Figure 5-26 x = at least 520 = 520, 521, 522, . . . . 520 519.5 x = more than 520 = 521, 522, 523, . . . 521 520.5 x = at most 520 = 0, 1, . . . 518, 519, 520 520 520.5 Figure 5-26 x = at least 520 = 520, 521, 522, . . . . 520 519.5 x = more than 520 = 521, 522, 523, . . . 521 520.5 x = at most 520 = 0, 1, . . . 518, 519, 520 520 520.5 x = fewer than 520 = 0, 1, . . . 518, 519 Figure 5-26 519 519.5 x = exactly 520 x = exactly 520 520 x = exactly 520 520 519.5 520.5 Interval represents discrete number 520 ELEMENTARY STATISTICS Chapter 6 Estimates and Sample Sizes MARIO F. TRIOLA EIGHTH EDITION Chapter 6 Estimates and Sample Sizes 6-1 Overview 6-2 Estimating a Population Mean: Large Samples 6-3 Estimating a Population Mean: Small Samples 6-4 Sample Size Required to Estimate µ 6-5 Estimating a Population Proportion 6-6 Estimating a Population Variance 6-1 Overview This chapter presents: methods for estimating population means, proportions, and variances methods for determining sample sizes 6-2 Estimating a Population Mean: Large Samples Assumptions n > 30 The sample must have more than 30 values. Simple Random Sample All samples of the same size have an equal chance of being selected. Assumptions n > 30 The sample must have more than 30 values. Simple Random Sample All samples of the same size have an equal chance of being selected. Data collected carelessly can be absolutely worthless, even if the sample is quite large. Estimator Definitions a formula or process for using sample data to estimate a population parameter Estimate a specific value or range of values used to approximate some population parameter Point Estimate a single value (or point) used to approximate a population parameter Estimator Definitions a formula or process for using sample data to estimate a population parameter Estimate a specific value or range of values used to approximate some population parameter Point Estimate a single value (or point) used to approximate a population parameter The sample mean x is the best point estimate of the population mean µ. Definition Confidence Interval (or Interval Estimate) a range (or an interval) of values used to estimate the true value of the population parameter Definition Confidence Interval (or Interval Estimate) a range (or an interval) of values used to estimate the true value of the population parameter Lower # < population parameter < Upper # Definition Confidence Interval (or Interval Estimate) a range (or an interval) of values used to estimate the true value of the population parameter Lower # < population parameter < Upper # As an example Lower # < m < Upper # Definition Degree of Confidence (level of confidence or confidence coefficient) the probability 1 - (often expressed as the equivalent percentage value) that is the relative frequency of times the confidence interval actually does contain the population parameter, assuming that the estimation process is repeated a large number of times usually 90%, 95%, or 99% ( = 10%), ( = 5%), ( = 1%) Interpreting a Confidence Interval 98.08 < µ < 98.32 o o Correct: We are 95% confident that the interval from 98.08 to 98.32 actually does contain the true value of m. This means that if we were to select many different samples of size 106 and construct the confidence intervals, 95% of them would actually contain the value of the population mean m. Wrong: There is a 95% chance that the true value of m will fall between 98.08 and 98.32. Confidence Intervals from 20 Different Samples Figure 6-1 Definition Critical Value the number on the borderline separating sample statistics that are likely to occur from those that are unlikely to occur. The number z/2 is a critical value that is a z score with the property that it separates an area /2 in the right tail of the standard normal distribution. The Critical Value 2 2 2 -z Figure 6-2 z 2 z=0 z 2 Found from Table A-2 (corresponds to area of 0.5 - 2 ) Finding z2 for 95% Degree of Confidence Finding z2 for 95% Degree of Confidence 95% = 5% 2 = 2.5% = .025 .95 .025 -z2 .025 z2 Finding z2 for 95% Degree of Confidence 95% = 5% 2 = 2.5% = .025 .95 .025 .025 z2 -z2 Critical Values Finding z2 for 95% Degree of Confidence Finding z2 for 95% Degree of Confidence = 0.05 = 0.025 .4750 .025 Use Table A-2 to find a z score of 1.96 Finding z2 for 95% Degree of Confidence = 0.05 = 0.025 .4750 .025 Use Table A-2 to find a z score of 1.96 z2 = 1.96 .025 - 1.96 .025 1.96 Definition Margin of Error Definition Margin of Error is the maximum likely difference observed between sample mean x and true population mean µ. denoted by E Definition Margin of Error is the maximum likely difference observed between sample mean x and true population mean µ. denoted by E x -E µ x +E Definition Margin of Error is the maximum likely difference observed between sample mean x and true population mean µ. denoted by E x -E µ x +E x -E < µ < x +E Definition Margin of Error is the maximum likely difference observed between sample mean x and true population mean µ. denoted by E x -E µ x +E x -E < µ < x +E lower limit upper limit Definition Margin of Error E = z/2 • x -E s Formula 6-1 n µ x +E Definition Margin of Error E = z/2 • x -E s Formula 6-1 n µ x +E also called the maximum error of the estimate Calculating E When s Is Unknown If n > 30, we can replace s in Formula 61 by the sample standard deviation s. If n 30, the population must have a normal distribution and we must know s to use Formula 6-1. Confidence Interval (or Interval Estimate) for Population Mean µ (Based on Large Samples: n >30) x -E <µ< x +E Confidence Interval (or Interval Estimate) for Population Mean µ (Based on Large Samples: n >30) x -E <µ< x +E µ=x +E Confidence Interval (or Interval Estimate) for Population Mean µ (Based on Large Samples: n >30) x -E <µ< x +E µ=x +E (x + E, x - E) Procedure for Constructing a Confidence Interval for µ ( Based on a Large Sample: n > 30 ) Procedure for Constructing a Confidence Interval for µ ( Based on a Large Sample: n > 30 ) 1. Find the critical value z2 that corresponds to the desired degree of confidence. Procedure for Constructing a Confidence Interval for µ ( Based on a Large Sample: n > 30 ) 1. Find the critical value z2 that corresponds to the desired degree of confidence. 2. Evaluate the margin of error E = z2 • s / n . If the population standard deviation s is unknown, use the value of the sample standard deviation s provided that n > 30. Procedure for Constructing a Confidence Interval for µ ( Based on a Large Sample: n > 30 ) 1. Find the critical value z2 that corresponds to the desired degree of confidence. 2. Evaluate the margin of error E = z2 • s / n . If the population standard deviation s is unknown, use the value of the sample standard deviation s provided that n > 30. 3. Find the values of x - E and x + E. Substitute those values in the general format of the confidence interval: x - E < µ < x + E Procedure for Constructing a Confidence Interval for µ ( Based on a Large Sample: n > 30 ) 1. Find the critical value z2 that corresponds to the desired degree of confidence. 2. Evaluate the margin of error E = z2 • s / n . If the population standard deviation s is unknown, use the value of the sample standard deviation s provided that n > 30. 3. Find the values of x - E and x + E. Substitute those values in the general format of the confidence interval: x - E < µ < x + E 4. Round using the confidence intervals roundoff rules. Round-Off Rule for Confidence Intervals Used to Estimate µ 1. When using the original set of data, round the confidence interval limits to one more decimal place than used in original set of data. Round-Off Rule for Confidence Intervals Used to Estimate µ 1. When using the original set of data, round the confidence interval limits to one more decimal place than used in original set of data. 2. When the original set of data is unknown and only the summary statistics (n, x, s) are used, round the confidence interval limits to the same number of decimal places used for the sample mean. Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.2o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.20o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 E = z / 2 • s n = 1.96 • 0.62 106 = 0.12 Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.20o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 E = z / 2 • s n = 1.96 • 0.62 106 = 0.12 x -E <m< x +E Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.20o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 E = z / 2 • s n = 1.96 • 0.62 106 = 0.12 x -E <m< x +E 98.20o - 0.12 <m< 98.20o + 0.12 Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.20o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 E = z / 2 • s n = 1.96 • 0.62 106 = 0.12 x -E <m< x +E 98.20o - 0.12 98.08o <m< <m< 98.20o + 0.12 98.32o Example: A study found the body temperatures of 106 healthy adults. The sample mean was 98.2 degrees and the sample standard deviation was 0.62 degrees. Find the margin of error E and the 95% confidence interval. n = 106 x = 98.20o s = 0.62o = 0.05 /2 = 0.025 z / 2 = 1.96 E = z / 2 • s n = 1.96 • 0.62 106 = 0.12 x -E <m< x +E 98.08o < m < 98.32o Based on the sample provided, the confidence interval for the m population mean is 98.08o < < 98.32o. If we were to select many different samples of the same size, 95% of the confidence intervals would actually contain the population mean m. Finding the Point Estimate and E from a Confidence Interval Point estimate of µ: x = (upper confidence interval limit) + (lower confidence interval limit) 2 Finding the Point Estimate and E from a Confidence Interval Point estimate of µ: x = (upper confidence interval limit) + (lower confidence interval limit) 2 Margin of Error: E = (upper confidence interval limit) - (lower confidence interval limit) 2 ELEMENTARY Section 6-3 STATISTICS Estimating a Population Mean: Small Samples MARIO F. TRIOLA EIGHTH EDITION Small Samples Assumptions If 1) n 30 2) The sample is a simple random sample. 3) The sample is from a normally distributed population. Case 1 (s is known): Largely unrealistic; Use methods from 6-2 Case 2 (sis unknown): Use Student t distribution Student t Distribution If the distribution of a population is essentially normal, then the distribution of t = x-µ s n Student t Distribution If the distribution of a population is essentially normal, then the distribution of t = x-µ s n is essentially a Student t Distribution for all samples of size n. is used to find critical values denoted by t/ 2 Table A - 3 Formulas and Tables Card Back cover Appendix Definition Degrees of Freedom (df ) corresponds to the number of sample values that can vary after certain restrictions have imposed on all data values Definition Degrees of Freedom (df ) corresponds to the number of sample values that can vary after certain restrictions have imposed on all data values df = n - 1 in this section Definition Degrees of Freedom (df ) = n - 1 corresponds to the number of sample values that can vary after certain restrictions have imposed on all data values Any Any Any Any Any Any Any Any Any Specific # # # # # # # # # # n = 10 df = 10 - 1 = 9 so that x = 80 Margin of Error E for Estimate of m Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population Margin of Error E for Estimate of m Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population Formula 6-2 E = t s 2 n where t/ 2 has n - 1 degrees of freedom Confidence Interval for the Estimate of E Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population Confidence Interval for the Estimate of E Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population x-E <µ< x +E Confidence Interval for the Estimate of E Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population x-E <µ< x +E where E = t/2 s n Confidence Interval for the Estimate of E Based on an Unknown s and a Small Simple Random Sample from a Normally Distributed Population x-E <µ< x +E where E = t/2 s n t/2 found in Table A-3 Table A-3 t Distribution Degrees of freedom 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Large (z) .005 (one tail) .01 (two tails) 63.657 9.925 5.841 4.604 4.032 3.707 3.500 3.355 3.250 3.169 3.106 3.054 3.012 2.977 2.947 2.921 2.898 2.878 2.861 2.845 2.831 2.819 2.807 2.797 2.787 2.779 2.771 2.763 2.756 2.575 .01 (one tail) .02 (two tails) 31.821 6.965 4.541 3.747 3.365 3.143 2.998 2.896 2.821 2.764 2.718 2.681 2.650 2.625 2.602 2.584 2.567 2.552 2.540 2.528 2.518 2.508 2.500 2.492 2.485 2.479 2.473 2.467 2.462 2.327 .025 (one tail) .05 (two tails) 12.706 4.303 3.182 2.776 2.571 2.447 2.365 2.306 2.262 2.228 2.201 2.179 2.160 2.145 2.132 2.120 2.110 2.101 2.093 2.086 2.080 2.074 2.069 2.064 2.060 2.056 2.052 2.048 2.045 1.960 .05 (one tail) .10 (two tails) .10 (one tail) .20 (two tails) .25 (one tail) .50 (two tails) 6.314 2.920 2.353 2.132 2.015 1.943 1.895 1.860 1.833 1.812 1.796 1.782 1.771 1.761 1.753 1.746 1.740 1.734 1.729 1.725 1.721 1.717 1.714 1.711 1.708 1.706 1.703 1.701 1.699 1.645 3.078 1.886 1.638 1.533 1.476 1.440 1.415 1.397 1.383 1.372 1.363 1.356 1.350 1.345 1.341 1.337 1.333 1.330 1.328 1.325 1.323 1.321 1.320 1.318 1.316 1.315 1.314 1.313 1.311 1.282 1.000 .816 .765 .741 .727 .718 .711 .706 .703 .700 .697 .696 .694 .692 .691 .690 .689 .688 .688 .687 .686 .686 .685 .685 .684 .684 .684 .683 .683 .675 Important Properties of the Student t Distribution 1. The Student t distribution is different for different sample sizes (see Figure 6-5 for the cases n = 3 and n = 12). 2. The Student t distribution has the same general symmetric bell shape as the normal distribution but it reflects the greater variability (with wider distributions) that is expected with small samples. 3. The Student t distribution has a mean of t = 0 (just as the standard normal distribution has a mean of z = 0). 4. The standard deviation of the Student t distribution varies with the sample size and is greater than 1 (unlike the standard normal distribution, which has a s = 1). 5. As the sample size n gets larger, the Student t distribution gets closer to the normal distribution. For values of n > 30, the differences are so small that we can use the critical z values instead of developing a much larger table of critical t values. (The values in the bottom row of Table A-3 are equal to the corresponding critical z values from the standard normal distribution.) Student t Distributions for n = 3 and n = 12 Student t Standard normal distribution distribution with n = 12 Student t distribution with n = 3 Figure 6-5 0 Using the Normal and t Distribution Figure 6-6 Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 Table A-3 t Distribution Degrees of freedom 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Large (z) .005 (one tail) .01 (two tails) 63.657 9.925 5.841 4.604 4.032 3.707 3.500 3.355 3.250 3.169 3.106 3.054 3.012 2.977 2.947 2.921 2.898 2.878 2.861 2.845 2.831 2.819 2.807 2.797 2.787 2.779 2.771 2.763 2.756 2.575 .01 (one tail) .02 (two tails) 31.821 6.965 4.541 3.747 3.365 3.143 2.998 2.896 2.821 2.764 2.718 2.681 2.650 2.625 2.602 2.584 2.567 2.552 2.540 2.528 2.518 2.508 2.500 2.492 2.485 2.479 2.473 2.467 2.462 2.327 .025 (one tail) .05 (two tails) 12.706 4.303 3.182 2.776 2.571 2.447 2.365 2.306 2.262 2.228 2.201 2.179 2.160 2.145 2.132 2.120 2.110 2.101 2.093 2.086 2.080 2.074 2.069 2.064 2.060 2.056 2.052 2.048 2.045 1.960 .05 (one tail) .10 (two tails) .10 (one tail) .20 (two tails) .25 (one tail) .50 (two tails) 6.314 2.920 2.353 2.132 2.015 1.943 1.895 1.860 1.833 1.812 1.796 1.782 1.771 1.761 1.753 1.746 1.740 1.734 1.729 1.725 1.721 1.717 1.714 1.711 1.708 1.706 1.703 1.701 1.699 1.645 3.078 1.886 1.638 1.533 1.476 1.440 1.415 1.397 1.383 1.372 1.363 1.356 1.350 1.345 1.341 1.337 1.333 1.330 1.328 1.325 1.323 1.321 1.320 1.318 1.316 1.315 1.314 1.313 1.311 1.282 1.000 .816 .765 .741 .727 .718 .711 .706 .703 .700 .697 .696 .694 .692 .691 .690 .689 .688 .688 .687 .686 .686 .685 .685 .684 .684 .684 .683 .683 .675 Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 t/2 = 2.201 E = t2 s = (2.201)(15,873) = 10,085.29 n 12 Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 t/2 = 2.201 E = t2 s = (2.201)(15,873) = 10,085.3 12 n x -E <µ< x +E Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 t/2 = 2.201 E = t2 s = (2.201)(15,873) = 10,085.3 n x -E 12 <µ< x +E 26,227 - 10,085.3 < µ < 26,227 + 10,085.3 Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 t/2 = 2.201 E = t2 s = (2.201)(15,873) = 10,085.3 n x -E 12 <µ< x +E 26,227 - 10,085.3 < µ < 26,227 + 10,085.3 $16,141.7 < µ < $36,312.3 Example: A study of 12 Dodge Vipers involved in collisions resulted in repairs averaging $26,227 and a standard deviation of $15,873. Find the 95% interval estimate of m, the mean repair cost for all Dodge Vipers involved in collisions. (The 12 cars’ distribution appears to be bell-shaped.) x = 26,227 s = 15,873 = 0.05 /2 = 0.025 t/2 = 2.201 E = t2 s = (2.201)(15,873) = 10,085.3 n 12 x -E <µ< x +E 26,227 - 10,085.3 < µ < 26,227 + 10,085.3 $16,141.7 < µ < $36,312.3 We are 95% confident that this interval contains the average cost of repairing a Dodge Viper. ELEMENTARY STATISTICS Section 6-4 Determining Sample Size Required to Estimate m MARIO F. TRIOLA EIGHTH EDITION Sample Size for Estimating Mean m Sample Size for Estimating Mean m s E = z/ 2 • n Sample Size for Estimating Mean m s E = z/ 2 • n (solve for n by algebra) Sample Size for Estimating Mean m s E = z/ 2 • n (solve for n by algebra) n= z/ 2 s E 2 Formula 6-3 Sample Size for Estimating Mean m s E = z/ 2 • n (solve for n by algebra) n= z/ 2 s 2 Formula 6-3 E z/2 = critical z score based on the desired degree of confidence E = desired margin of error s = population standard deviation Round-Off Rule for Sample Size n Round-Off Rule for Sample Size n When finding the sample size n, if the use of Formula 6-3 does not result in a whole number, always increase the value of n to the next larger whole number. Round-Off Rule for Sample Size n When finding the sample size n, if the use of Formula 6-3 does not result in a whole number, always increase the value of n to the next larger whole number. n = 216.09 = 217 (rounded up) Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) = 0.01 z = 2.575 E = 0.25 s = 1.065 Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) 2 2 = 0.01 z = 2.575 E = 0.25 s = 1.065 n = zs E = (2.575)(1.065) 0.25 Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) 2 2 = 0.01 z = 2.575 E = 0.25 s = 1.065 n = zs E = (2.575)(1.065) 0.25 = 120.3 = 121 households Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) 2 2 = 0.01 z = 2.575 E = 0.25 s = 1.065 n = zs E = (2.575)(1.065) 0.25 = 120.3 = 121 households If n is not a whole number, round it up to the next higher whole number. Example: If we want to estimate the mean weight of plastic discarded by households in one week, how many households must be randomly selected to be 99% confident that the sample mean is within 0.25 lb of the true population mean? (A previous study indicates the standard deviation is 1.065 lb.) 2 2 = 0.01 z = 2.575 E = 0.25 s = 1.065 n = zs E = (2.575)(1.065) 0.25 = 120.3 = 121 households We would need to randomly select 121 households and obtain the average weight of plastic discarded in one week. We would be 99% confident that this mean is within 1/4 lb of the population mean. What if sis Not Known ? 1. Use the range rule of thumb to estimate the standard deviation as follows: s range 4 What if sis Not Known ? 1. Use the range rule of thumb to estimate the standard deviation as follows: s range 4 2. Conduct a pilot study by starting the sampling process. Based on the first collection of at least 31 randomly selected sample values, calculate the sample standard deviation s and use it in place of s. That value can be refined as more sample data are obtained. What if sis Not Known ? 1. Use the range rule of thumb to estimate the standard deviation as follows: s range 4 2. Conduct a pilot study by starting the sampling process. Based on the first collection of at least 31 randomly selected sample values, calculate the sample standard deviation s and use it in place of s. That value can be refined as more sample data are obtained. 3. Estimate the value of s by using the results of some other study that was done earlier. What happens when E is doubled ? What happens when E is doubled ? 2 2 (z/ 2s ) z/ 2 s E=1: n= 1 = 1 What happens when E is doubled ? 2 2 (z/ 2s ) z/ 2 s E=1: n= E=2: (z/ 2s ) z / 2 s n= = 4 2 1 = 2 1 2 Sample size n is decreased to 1/4 of its original value if E is doubled. Larger errors allow smaller samples. Smaller errors require larger samples. ELEMENTARY Section 6-5 Proportion STATISTICS Estimating a Population MARIO F. TRIOLA EIGHTH EDITION Assumptions 1. The sample is a simple random sample. 2. The conditions for the binomial distribution are satisfied (See Section 4-3.) 3. The normal distribution can be used to approximate the distribution of sample proportions because np 5 and nq 5 are both satisfied. Notation for Proportions Notation for Proportions p= population proportion Notation for Proportions p= ˆp = xn (pronounced ‘p-hat’) population proportion sample proportion of x successes in a sample of size n Notation for Proportions p= ˆp = xn population proportion sample proportion of x successes in a sample of size n (pronounced ‘p-hat’) qˆ = 1 - pˆ = sample proportion of x failures in a sample size of n Definition Point Estimate Definition Point Estimate The sample proportion p ˆ is the best point estimate of the population proportion p. Margin of Error of the Estimate of p Formula 6-4 E = z pˆ qˆ n Confidence Interval for Population Proportion pˆ - E < p < p̂ + E where E = z pˆ qˆ n Confidence Interval for Population Proportion pˆ - E < p < p̂ + E p = pˆ + E Confidence Interval for Population Proportion pˆ - E < p < p̂ + E p = pˆ + E (pˆ - E, pˆ + E) Round-Off Rule for Confidence Interval Estimates of p Round the confidence interval limits to three significant digits. Determining Sample Size Determining Sample Size E= z pˆ qˆ n Determining Sample Size E= z pˆ qˆ n (solve for n by algebra) Determining Sample Size E= z pˆ qˆ n (solve for n by algebra) n= ( z pˆ qˆ 2 ) E2 Sample Size for Estimating Proportion p ˆ When an estimate of p is known: n= ( 2 pq ) z ˆ ˆ E2 Formula 6-5 Sample Size for Estimating Proportion p ˆ When an estimate of p is known: n= ( 2 pq ) z ˆ ˆ Formula 6-5 E2 When no estimate of p is known: n= ( 2 0.25 ) z E2 Formula 6-6 pˆ qˆ pˆ qˆ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.09 0.16 0.21 0.24 0.25 0.24 0.21 0.16 0.09 pˆ qˆ pˆ qˆ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.09 0.16 0.21 0.24 0.25 0.24 0.21 0.16 0.09 Two formulas for proportion sample size n= n= ( z )2 pˆ qˆ E2 ( z (0.25) 2 ) E2 Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? A 1997 study indicates 16.9% of U.S. households used e-mail. Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? A 1997 study indicates 16.9% of U.S. households used e-mail. ˆ n = [z/2 ]2 p q̂ E2 Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? A 1997 study indicates 16.9% of U.S. households used e-mail. ˆˆ n = [z/2 ]2 p q E2 = [1.645]2 (0.169)(0.831) 0.042 Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? A 1997 study indicates 16.9% of U.S. households used e-mail. ˆˆ n = [z/2 ]2 p q E2 = [1.645]2 (0.169)(0.831) 0.042 = 237.51965 = 238 households To be 90% confident that our sample percentage is within four percentage points of the true percentage for all households, we should randomly select and survey 238 households. Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? There is no prior information suggesting a possible value for the sample percentage. Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? There is no prior information suggesting a possible value for the sample percentage. n = [z/2 ]2 (0.25) E2 Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? There is no prior information suggesting a possible value for the sample percentage. n = [z/2 ]2 (0.25) E2 = (1.645)2 (0.25) 0.042 = 422.81641 = 423 households Example: We want to determine, with a margin of error of four percentage points, the current percentage of U.S. households using e-mail. Assuming that we want 90% confidence in our results, how many households must we survey? There is no prior information suggesting a possible value for the sample percentage. n = [z/2 ]2 (0.25) E2 = (1.645)2 (0.25) 0.042 = 422.81641 = 423 households With no prior information, we need a larger sample to achieve the same results with 90% confidence and an error of no more than 4%. Finding the Point Estimate and E from a Confidence Interval ˆ (upper confidence interval limit) + (lower confidence interval limit) Point estimate of p: ˆ p= 2 Finding the Point Estimate and E from a Confidence Interval ˆ (upper confidence interval limit) + (lower confidence interval limit) Point estimate of p: ˆ p= 2 Margin of Error: E = (upper confidence interval limit) - (lower confidence interval limit) 2 ELEMENTARY STATISTICS Section 6-6Estimating a Population Variance MARIO F. TRIOLA EIGHTH EDITION Assumptions 1. The sample is a simple random sample. 2. The population must have normally distributed values (even if the sample is large). Chi-Square Distribution Chi-Square Distribution X = 2 (n - 1) s 2 s2 Formula 6-7 where n = sample size s 2 = sample variance s2 = population variance X2 Critical Values found in Table A-4 Formula card Appendix Degrees of freedom (df ) = n - 1 Properties of the Distribution of the Chi-Square Statistic 1. The chi-square distribution is not symmetric, unlike the normal and Student t distributions. Properties of the Distribution of the Chi-Square Statistic 1. The chi-square distribution is not symmetric, unlike the normal and Student t distributions. Not symmetric 0 All values are nonnegative Figure 6-7 Chi-Square Distribution x2 Properties of the Distribution of the Chi-Square Statistic 1. The chi-square distribution is not symmetric, unlike the normal and Student t distributions. As the number of degrees of freedom increases, the distribution becomes more symmetric. (continued) df = 10 Not symmetric df = 20 0 All values are nonnegative Figure 6-7 Chi-Square Distribution x2 0 5 10 15 20 25 30 35 40 45 Figure 6-8 Chi-Square Distribution for df = 10 and df = 20 Properties of the Distribution of the Chi-Square Statistic (continued) 2. The values of chi-square can be zero or positive, but they cannot be negative. 3. The chi-square distribution is different for each number of degrees of freedom, which is df = n - 1 in this section. As the number increases, the chisquare distribution approaches a normal distribution. In Table A-4, each critical value of X2 corresponds to an area given in the top row of the table, and that area represents the total region located to the right of the critical value. Degrees of freedom 2 Table A-4 Chi-Square (x ) Distribution Area to the Right of the Critical Value 0.995 0.99 0.975 0.95 0.90 0.10 0.05 0.025 0.01 0.005 1 2 3 4 5 _ 0.010 0.072 0.207 0.412 _ 0.020 0.115 0.297 0.554 0.001 0.051 0.216 0.484 0.831 0.004 0.103 0.352 0.711 1.145 0.016 0.211 0.584 1.064 1.610 2.706 4.605 6.251 7.779 9.236 3.841 5.991 7.815 9.488 11.071 5.024 7.378 9.348 11.143 12.833 6.635 9.210 11.345 13.277 15.086 7.879 10.597 12.838 14.860 16.750 6 7 8 9 10 0.676 0.989 1.344 1.735 2.156 0.872 1.239 1.646 2.088 2.558 1.237 1.690 2.180 2.700 3.247 1.635 2.167 2.733 3.325 3.940 2.204 2.833 3.490 4.168 4.865 10.645 12.017 13.362 14.684 15.987 12.592 14.067 15.507 16.919 18.307 14.449 16.013 17.535 19.023 20.483 16.812 18.475 20.090 21.666 23.209 18.548 20.278 21.955 23.589 25.188 11 12 13 14 15 2.603 3.074 3.565 4.075 4.601 3.053 3.571 4.107 4.660 5.229 3.816 4.404 5.009 5.629 6.262 4.575 5.226 5.892 6.571 7.261 5.578 6.304 7.042 7.790 8.547 17.275 18.549 19.812 21.064 22.307 19.675 21.026 22.362 23.685 24.996 21.920 23.337 24.736 26.119 27.488 24.725 26.217 27.688 29.141 30.578 26.757 28.299 29.819 31.319 32.801 16 17 18 19 20 5.142 5.697 6.265 6.844 7.434 5.812 6.408 7.015 7.633 8.260 6.908 7.564 8.231 8.907 9.591 7.962 8.672 9.390 10.117 10.851 9.312 10.085 10.865 11.651 12.443 23.542 24.769 25.989 27.204 28.412 26.296 27.587 28.869 30.144 31.410 28.845 30.191 31.526 32.852 34.170 32.000 33.409 34.805 36.191 37.566 34.267 35.718 37.156 38.582 39.997 21 22 23 24 25 8.034 8.643 9.260 9.886 10.520 8.897 9.542 10.196 10.856 11.524 10.283 10.982 11.689 12.401 13.120 11.591 12.338 13.091 13.848 14.611 13.240 14.042 14.848 15.659 16.473 29.615 30.813 32.007 33.196 34.382 32.671 33.924 35.172 36.415 37.652 35.479 36.781 38.076 39.364 40.646 38.932 40.289 41.638 42.980 44.314 41.401 42.796 44.181 45.559 46.928 26 27 28 29 30 11.160 11.808 12.461 13.121 13.787 12.198 12.879 13.565 14.257 14.954 13.844 14.573 15.308 16.047 16.791 15.379 16.151 16.928 17.708 18.493 17.292 18.114 18.939 19.768 20.599 35.563 36.741 37.916 39.087 40.256 38.885 40.113 41.337 42.557 43.773 41.923 43.194 44.461 45.722 46.979 45.642 46.963 48.278 49.588 50.892 48.290 49.645 50.993 52.336 53.672 40 50 60 70 80 90 100 20.707 27.991 35.534 43.275 51.172 59.196 67.328 22.164 29.707 37.485 45.442 53.540 61.754 70.065 24.433 32.357 40.482 48.758 57.153 65.647 74.222 26.509 34.764 43.188 51.739 60.391 69.126 77.929 29.051 37.689 46.459 55.329 64.278 73.291 82.358 51.805 63.167 74.397 85.527 96.578 107.565 118.498 55.758 67.505 79.082 90.531 101.879 113.145 124.342 59.342 71.420 83.298 95.023 106.629 118.136 129.561 63.691 76.154 88.379 100.425 112.329 124.116 135.807 66.766 79.490 91.952 104.215 116.321 128.299 140.169 Critical Values: Table A-4 Areas to the right of each tail 0.975 0.025 0.025 0.025 0 XL2 = 2.700 2 X2 (df = 9) XR = 19.023 Estimators of s 2 The sample variance s is the best point estimate of the population variance s . 2 2 Confidence Interval for the 2 Population Variance s Confidence Interval for the 2 Population Variance s (n - 1)s 2 X 2 R s2 (n - 1)s 2 X 2 L Confidence Interval for the 2 Population Variance s (n - 1)s 2 Right-tail CV X 2 R s2 (n - 1)s 2 X 2 L Confidence Interval for the 2 Population Variance s (n - 1)s 2 Right-tail CV X 2 R s2 (n - 1)s 2 X 2 L Left-tail CV Confidence Interval for the 2 Population Variance s (n - 1)s 2 X Right-tail CV 2 R s2 (n - 1)s 2 X 2 L Left-tail CV Confidence Interval for the Population Standard Deviation (n - 1)s 2 X 2 R s (n - 1)s 2 2 XL s Roundoff Rule for Confidence Interval Estimates of s or s2 1. When using the original set of data to construct a confidence interval, round the confidence interval limits to one more decimal place than is used for the original set of data. 2. When the original set of data is unknown and only the summary statistics (n, s) are used, round the confidence interval limits to the same number of decimals places used for the sample standard deviation or variance. Table 6-3 Determining Sample Size Table 6-3 Determining Sample Size Sample Size for s2 To be 95% confident that s2 is within 1% 5% 10% 20% 30% 40% 50% To be 95% confident that s2 is within 1% 5% 10% 20% 30% 40% 50% of the value of s2 , the sample size n should be at least 77,207 3,148 805 210 97 56 57 of the value of s2 , the sample size n should be at least 133,448 5,457 1,401 368 171 100 67 Sample Size for s To be 95% confident that s is within 1% 5% 10% 20% 30% 40% 50% To be 95% confident that s is within 1% 5% 10% 20% 30% 40% 50% of the value of s , the sample size n should be at least 19,204 767 191 47 20 11 7 of the value of s , the sample size n should be at least 33,218 1,335 335 84 37 21 13 ELEMENTARY STATISTICS Chapter 7 Hypothesis Testing MARIO F. TRIOLA EIGHTH EDITION Chapter 7 Hypothesis Testing 7-1 Overview 7-2 Fundamentals of Hypothesis Testing 7-3 Testing a Claim about a Mean: Large Samples 7-4 Testing a Claim about a Mean: Small Samples 7-5 Testing a Claim about a Proportion 7-6 Testing a Claim about a Standard Deviation 7-1 Overview Definition Hypothesis in statistics, is a claim or statement about a property of a population Rare Event Rule for Inferential Statistics If, under a given assumption, the probability of a particular observed event is exceptionally small, we conclude that the assumption is probably not correct. 7-2 Fundamentals of Hypothesis Testing Figure 7-1 Central Limit Theorem Figure 7-1 Central Limit Theorem The Expected Distribution of Sample Means Assuming that m = 98.6 Likely sample means µx = 98.6 Figure 7-1 Central Limit Theorem The Expected Distribution of Sample Means Assuming that m = 98.6 Likely sample means µx = 98.6 z = - 1.96 or x = 98.48 z= 1.96 or x = 98.72 Figure 7-1 Central Limit Theorem The Expected Distribution of Sample Means Assuming that m = 98.6 Sample data: z = - 6.64 or x = 98.20 Likely sample means µx = 98.6 z = - 1.96 or x = 98.48 z= 1.96 or x = 98.72 Components of a Formal Hypothesis Test Null Hypothesis: H0 Statement about value of population parameter Must contain condition of equality =, , or Test the Null Hypothesis directly Reject H0 or fail to reject H0 Alternative Hypothesis: H1 Must be true if H0 is false , <, > ‘opposite’ of Null Note about Forming Your Own Claims (Hypotheses) If you are conducting a study and want to use a hypothesis test to support your claim, the claim must be worded so that it becomes the alternative hypothesis. Note about Testing the Validity of Someone Else’s Claim Someone else’s claim may become the null hypothesis (because it contains equality), and it sometimes becomes the alternative hypothesis (because it does not contain equality). Test Statistic a value computed from the sample data that is used in making the decision about the rejection of the null hypothesis Test Statistic a value computed from the sample data that is used in making the decision about the rejection of the null hypothesis For large samples, testing claims about population means z= x - µx s n Critical Region Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Region Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Region Critical Region Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Region Critical Region Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Regions Significance Level denoted by the probability that the test statistic will fall in the critical region when the null hypothesis is actually true. common choices are 0.05, 0.01, and 0.10 Critical Value Value or values that separate the critical region (where we reject the null hypothesis) from the values of the test statistics that do not lead to a rejection of the null hypothesis Critical Value Value or values that separate the critical region (where we reject the null hypothesis) from the values of the test statistics that do not lead to a rejection of the null hypothesis Critical Value ( z score ) Critical Value Value or values that separate the critical region (where we reject the null hypothesis) from the values of the test statistics that do not lead to a rejection of the null hypothesis Reject H0 Critical Value ( z score ) Fail to reject H0 Two-tailed,Right-tailed, Left-tailed Tests The tails in a distribution are the extreme regions bounded by critical values. Two-tailed Test H0: µ = 100 H1: µ 100 Two-tailed Test H0: µ = 100 H1: µ 100 is divided equally between the two tails of the critical region Two-tailed Test H0: µ = 100 H1: µ 100 is divided equally between the two tails of the critical region Means less than or greater than Two-tailed Test H0: µ = 100 H1: µ 100 is divided equally between the two tails of the critical region Means less than or greater than Reject H0 Fail to reject H0 Reject H0 100 Values that differ significantly from 100 Right-tailed Test H0: µ 100 H1: µ > 100 Right-tailed Test H0: µ 100 H1: µ > 100 Points Right Right-tailed Test H0: µ 100 H1: µ > 100 Points Right Fail to reject H0 100 Reject H0 Values that differ significantly from 100 Left-tailed Test H0: µ 100 H1: µ < 100 Left-tailed Test H0: µ 100 H1: µ < 100 Points Left Left-tailed Test H0: µ 100 H1: µ < 100 Points Left Reject H0 Values that differ significantly from 100 Fail to reject H0 100 Conclusions in Hypothesis Testing always test the null hypothesis 1. Reject the H0 2. Fail to reject the H0 need to formulate correct wording of final conclusion See Figure 7-4 Wording of Final Conclusion FIGURE 7-4 Start Does the original claim contain the condition of equality Yes (Original claim contains equality and becomes H0) No Do you reject H0?. “There is sufficient evidence to warrant (Reject H0) rejection of the claim that. . . (original claim).” Yes No (Fail to reject H0) (Original claim does not contain equality and becomes H1) Do you reject H0? Yes (Reject H0) “There is not sufficient evidence to warrant rejection of the claim that. . . (original claim).” “The sample data supports the claim that . . . (original claim).” No (Fail to reject H0) (This is the only case in which the original claim is rejected). “There is not sufficient evidence to support the claim that. . . (original claim).” (This is the only case in which the original claim is supported). Accept versus Fail to Reject some texts use “accept the null hypothesis we are not proving the null hypothesis sample evidence is not strong enough to warrant rejection (such as not enough evidence to convict a suspect) Type I Error The mistake of rejecting the null hypothesis when it is true. (alpha) is used to represent the probability of a type I error Example: Rejecting a claim that the mean body temperature is 98.6 degrees when the mean really does equal 98.6 Type II Error the mistake of failing to reject the null hypothesis when it is false. ß (beta) is used to represent the probability of a type II error Example: Failing to reject the claim that the mean body temperature is 98.6 degrees when the mean is really different from 98.6 Table 7-2 Type I and Type II Errors True State of Nature We decide to reject the null hypothesis The null hypothesis is true The null hypothesis is false Type I error (rejecting a true null hypothesis) Correct decision Correct decision Type II error (rejecting a false null hypothesis) Decision We fail to reject the null hypothesis Controlling Type I and Type II Errors For any fixed , an increase in the sample size n will cause a decrease in For any fixed sample size n , a decrease in will cause an increase in . Conversely, an increase in will cause a decrease in . To decrease both and , increase the sample size. Definition Power of a Hypothesis Test is the probability (1 - ) of rejecting a false null hypothesis, which is computed by using a particular significance level and a particular value of the mean that is an alternative to the value assumed true in the null hypothesis. ELEMENTARY Section 7-3 STATISTICS Testing a Claim about a Mean: Large Samples MARIO F. TRIOLA EIGHTH EDITION Three Methods Discussed 1) Traditional method 2) P-value method 3) Confidence intervals Assumptions for testing claims about population means 1) The sample is a simple random sample. 2) The sample is large (n > 30). a) Central limit theorem applies b) Can use normal distribution 3) If s is unknown, we can use sample standard deviation s as estimate for s. Traditional (or Classical) Method of Testing Hypotheses Goal Identify a sample result that is significantly different from the claimed value The traditional (or classical) method of hypothesis testing converts the relevant sample statistic into a test statistic which we compare to the critical value. Test Statistic for Claims about µ when n > 30 (Step 6) z= x - µx s n Traditional (or Classical) Method of Testing Hypotheses Figure 7-5 1. Identify the specific claim or hypothesis to be tested, and put it in symbolic form. 2. Give the symbolic form that must be true when the original claim is false. 3. Of the two symbolic expressions obtained so far, let null hypothesis H0 be the one that contains the condition of equality. H1 is the other statement. 4. Select the significant level based on the seriousness of a type I error. Make small if the consequences of rejecting a true H0 are severe. The values of 0.05 and 0.01 are very common. 5. Identify the statistic that is relevant to this test and its sampling distribution. 6. Determine the test statistic, the critical values, and the critical region. Draw a graph and include the test statistic, critical value(s), and critical region. 7. Reject H0 if the test statistic is in the critical region. Fail to reject H0 if the test statistic is not in the critical region. 8. Restate this previous decision in simple nontechnical terms. (See Figure 7-4) Traditional (or Classical) Method of Testing Hypotheses Figure 7-5 1. Identify the specific claim or hypothesis to be tested, and put it in symbolic form. 2. Give the symbolic form that must be true when the original claim is false. 3. Of the two symbolic expressions obtained so far, let null hypothesis H0 be the one that contains the condition of equality. H1 is the other statement. 4. Select the significant level based on the seriousness of a type I error. Make small if the consequences of rejecting a true H0 are severe. The values of 0.05 and 0.01 are very common. 5. Identify the statistic that is relevant to this test and its sampling distribution. 6. Determine the test statistic, the critical values, and the critical region. Draw a graph and include the test statistic, critical value(s), and critical region. 7. Reject H0 if the test statistic is in the critical region. Fail to reject H0 if the test statistic is not in the critical region. 8. Restate this previous decision in simple nontechnical terms. (See Figure 7-4) Decision Criterion (Step 7) Reject the null hypothesis if the test statistic is in the critical region Fail to reject the null hypothesis if the test statistic is not in the critical region FIGURE 7-4 Wording of Final Conclusion Start Yes Does the Yes (This “There is sufficient Do original claim(Original contain claim is the you reject to warrant (Rejectevidence H0) H0?.No the conditioncontains of only rejection of the claim equality (Fail to No “There is notcase sufficient equality that. . . (original claim).” and becomes H ) reject H0) evidence to warrant 0 (Original claim in does not contain rejection of the claim which (This is th equality and Yes that. . (original claim).” Do the “The . sample data only case becomes H1) you reject (Rejectsupports H0) origin the claim that No which the H0? . . . (originalalclaim).” (Fail to cla “There is not original sufficient claim reject H0) support evidence to is support is the claim reject Example: Given a data set of 106 healthy body temperatures, where the mean was 98.2o and s = 0.62o , at the 0.05 significance level, test the claim that the mean body temperature of all healthy adults is equal to 98.6o. Example: Given a data set of 106 healthy body temperatures, where the mean was 98.2o and s = 0.62o , at the 0.05 significance level, test the claim that the mean body temperature of all healthy adults is equal to 98.6o. Steps: 1,2,3) Set up Claim, H0, H1 Claim: m = 98.6o H0 : m = 98.6o H1 : m 98.6o Example: Given a data set of 106 healthy body temperatures, where the mean was 98.2o and s = 0.62o , at the 0.05 significance level, test the claim that the mean body temperature of all healthy adults is equal to 98.6o. Steps: 1,2,3) Set up Claim, H0, H1 Claim: m = 98.6o H0 : m = 98.6o H1 : m 98.6o 4) Select if necessary level: = 0.05 was given 5 & 6) Identify the test statistic z = x-µ = s n 98.2 - 98.6 0.62 106 = - 6.64 6) Determine critical region(s) and critical value(s) = 0.05 /2 = 0.025 (two tailed test) 0.4750 0.025 z = - 1.96 0.4750 0.025 1.96 Critical Values - Use Table A-2 6) Draw graph and include the test statistic, critical value(s), and critical region Sample data: x = 98.2o or z = - 6.64 Reject H0: µ = 98.6 z = - 1.96 Fail to Reject H0: µ = 98.6 µ = 98.6 Reject H0: µ = 98.6 z = 1.96 or z = 0 z = - 6.64 Figure 7-6 7) Reject H0: if TS is in critical region Fail to reject H0: if TS is not in critical region Sample data: x = 98.2o or z = - 6.64 Reject H0: µ = 98.6 z = - 1.96 Fail to Reject H0: µ = 98.6 µ = 98.6 Reject H0: µ = 98.6 z = 1.96 or z = 0 z = - 6.64 Figure 7-6 7) Reject H0: if TS is in critical region Fail to reject H0: if TS is not in critical region Sample data: x = 98.2o or z = - 6.64 Reject H0: µ = 98.6 z = - 1.96 Fail to Reject H0: µ = 98.6 µ = 98.6 Reject H0: µ = 98.6 z = 1.96 or z = 0 z = - 6.64 REJECT H0 Figure 7-6 8) Restate in simple nontechnical terms - Figure 7-4 Claim: m = 98.6o REJECT H0 : m = 98.6o H1 : m 98.6o 8) Restate in simple nontechnical terms - Figure 7-4 Start Yes Does the “There is sufficient (This is t Yes Do original claim(Original contain claimyou reject to warrant (Reject Hevidence only cas 0) H0? the conditioncontains of rejection of the which claim th equality “There is not sufficient No No equality? that. . . (originaloriginal claim).” and becomes H ) evidence to warrant (Original claim (Fail to0 is rejecte rejection of the claim does not containreject H0 ) (This is Yes Do “The dataclaim).” that. sample . . (original equality and only cas (Reject support H0) you reject the claim that becomes H1 ) No which th H0? . . . (original claim).” (Fail to original “There is not sufficient reject H0 ) evidence to support Figure 7-4 is suppo the claim that. . . (original claim).” 8) Restate in simple nontechnical terms - Figure 7-4 Start Yes Does the “There is sufficient (This is t Yes Do original claim containclaimyou reject to warrant (Original (Reject Hevidence only cas 0) H0? the conditioncontains of rejection of the which claim th equality “There is not sufficient No No equality? and becomes H ) that. . . (originaloriginal claim).” evidence to warrant (Original claim (Fail to0 is rejecte rejection of the claim does not containreject H0 ) (This is Yes Do “The dataclaim).” that. sample . . (original equality and only cas (Reject support H0) you reject the claim that becomes H1 ) No which th H0? . . . (original claim).” (Fail to original “There is not sufficient reject H0 ) Figure 7-4 is suppo evidence to support the claim that. . . (original claim).” 8) Restate in simple nontechnical terms - Figure 7-4 Start Yes Does the “There is sufficient (This is t Yes Do original claim containclaim to warrant (Original you reject (Reject Hevidence only cas 0) H0? the conditioncontains of rejection of the which claim th equality “There is not sufficient No No equality? and becomes H ) that. . . (originaloriginal claim).” (Fail to evidence to warrant 0 (Original claim is rejecte reject H ) rejection of the claim does not contain 0 (This is Yes Do “The dataclaim).” that. sample . . (original equality and only cas (Reject H ) you reject 0 support the claim that becomes H1 ) No which th H0? . . . (original claim).” (Fail to original “There is not sufficient reject H0 ) evidence to support Figure 7-4 is suppo the claim that. . . (original claim).” 8) Restate in simple nontechnical terms - Figure 7-4 Start Yes “There is sufficient Does the Yes (This is t Do evidence to warrant original claim containclaim (Original you reject only cas (Reje H0? rejection of thewhich claimth the conditioncontains of equality “There is not sufficient No ct H ) No 0 that. . . (original claim) equality? and becomes H ) original evidence to warrant 0(Fail to (Original claim is rejecte reject H ) rejection of the claim does not contain 0 (This is Yes Do “The dataclaim).” that. sample . . (original equality and only cas (Reject H ) you reject 0 support the claim that becomes H1 ) No which th H0? . . . (original claim).” (Fail to original “There is not sufficient reject H0 ) Figure 7-4 is suppo evidence to support the claim that. . . (original claim).” 8) Restate in simple nontechnical terms - Figure 7-4 Start There is sufficient evidence to warrant rejection of claim that the mean body temperatures of healthy adults is equal to 98.6 o. Yes Does the “There is sufficient Yes (This is t Do original claim containclaim (Original you reject only cas (Reje evidence to warrant H0? the conditioncontains of rejection of thewhich claimth equality “There is not sufficient No ct H ) No 0 equality? and becomes H ) that. . . (original claim) original (Fail to evidence to warrant 0 (Original claim is rejecte reject H ) rejection of the claim does not contain 0 (This is Yes Do “The dataclaim).” that. sample . . (original equality and only cas (Reject H ) you reject 0 support the claim that becomes H0 ) No which th H0? . . . (original claim).” (Fail to original “There is not sufficient reject H0 ) Figure 7-4 is suppo evidence to support the claim that. . . (original claim).” P-Value Method of Testing Hypotheses very similar to traditional method key difference is the way in which we decide to reject the null hypothesis approach finds the probability (P-value) of getting a result and rejects the null hypothesis if that probability is very low P-Value Method of Testing Hypotheses Definition P-Value (or probability value) the probability of getting a value of the sample test statistic that is at least as extreme as the one found from the sample data, assuming that the null hypothesis is true P-value Interpretation Small P-values (such as 0.05 or lower) Unusual sample results. Significant difference from the null hypothesis Large P-values (such as above 0.05) Sample results are not unusual. Not a significant difference from the null hypothesis Figure 7-8 Finding P-Values Start What type of test ? Left-tailed Right-tailed Two-tailed Left P-value = area to the left of the test statistic P-value µ Test statistic Is the test statistic to the right or left of center ? P-value = twice the area to the left of the test statistic P-value is twice this area µ Test statistic Right P-value = twice the area to the right of the test statistic P-value = area to the right of the test statistic P-value is twice this area P-value µ µ Test statistic Test statistic Procedure is the same except for steps 6 and 7 Step 6: Find the P-value (as shown in Figure 7-8) Step 7: Report the P-value Reject the null hypothesis if the P-value is less than or equal to the significance level Fail to reject the null hypothesis if the P-value is greater than the significance level Testing Claims with Confidence Intervals A confidence interval estimate of a population parameter contains the likely values of that parameter. We should therefore reject a claim that the population parameter has a value that is not included in the confidence interval. Testing Claims with Confidence Intervals Claim: mean body temperature = 98.6º, where n = 106, x = 98.2º and s = 0.62º 95% confidence interval of 106 body temperature data (that is, 95% of samples would contain true value µ ) 98.08º < µ < 98.32º 98.6º is not in this interval Therefore it is very unlikely that µ = 98.6º Thus we reject claim µ = 98.6º Underlying Rationale of Hypotheses Testing If, under a given observed assumption, the probability of getting the sample is exceptionally small, we conclude that the assumption is probably not correct. When testing a claim, we make an assumption (null hypothesis) that contains equality. We then compare the assumption and the sample results and we form one of the following conclusions: Underlying Rationale of Hypotheses Testing If the sample results can easily occur when the assumption (null hypothesis) is true, we attribute the relatively small discrepancy between the assumption and the sample results to chance. If the sample results cannot easily occur when that assumption (null hypothesis) is true, we explain the relatively large discrepancy between the assumption and the sample by concluding that the assumption is not true. ELEMENTARY Section 7-4 STATISTICS Testing a Claim about a Mean: Small Samples MARIO F. TRIOLA EIGHTH EDITION Assumptions for testing claims about population means 1) The sample is a simple random sample. 2) The sample is small (n 30). 3) The value of the population standard deviation s is unknown. 4) The sample values come from a population with a distribution that is approximately normal. Test Statistic for a Student t-distribution x -µx t= s n Critical Values Found in Table A-3 Degrees of freedom (df) = n -1 Critical t values to the left of the mean are negative Important Properties of the Student t Distribution 1. The Student t distribution is different for different sample sizes (see Figure 6-5 in Section 6-3). 2. The Student t distribution has the same general bell shape as the normal distribution; its wider shape reflects the greater variability that is expected with small samples. 3. The Student t distribution has a mean of t = 0 (just as the standard normal distribution has a mean of z = 0). 4. The standard deviation of the Student t distribution varies with the sample size and is greater than 1 (unlike the standard normal distribution, which has a s = 1). 5. As the sample size n gets larger, the Student t distribution get closer to the normal distribution. For values of n > 30, the differences are so small that we can use the critical z values instead of developing a much larger table of critical t values. (The values in the bottom row of Table A-3 are equal to the corresponding critical z values from the normal distributions.) Figure 7-11 Choosing between the Normal and Student t-Distributions when Testing a Claim about a Population Mean µ Start Use normal distribution with Is n > 30 ? Yes Z (If s is unknown use s instead.) No Is the distribution of the population essentially normal ? (Use a histogram.) No Yes Is s known ? No Use the Student t distribution with x - µx t s/ n x - µx s/ n Use nonparametric methods, which don’t require a normal distribution. Use normal distribution with Z x - µx s/ n (This case is rare.) The larger Student t critical value shows that with a small sample, the sample evidence must be more extreme before we consider the difference is significant. P-Value Method Table A-3 includes only selected values of Specific P-values usually cannot be found Use Table to identify limits that contain the P-value Some calculators and computer programs will find exact P-values ELEMENTARY Section 7-5 STATISTICS Testing a Claim about a Proportion MARIO F. TRIOLA EIGHTH EDITION Assumptions for testing claims about population proportions 1) The sample observations are a simple random sample. 2) The conditions for a binomial experiment are satisfied (Section 4-3) Assumptions for testing claims about population proportions 1) The sample observations are a simple random sample. 2) The conditions for a binomial experiment are satisfied (Section 4-3) 3) The condition np 5 and nq 5 are satisfied, so the binomial distribution of sample proportions can be approximated by a normal distribution with µ = np and s = npq Notation n = number of trials Notation n = number of trials p = x/n (sample proportion) p = population proportion (used in the q=1-p null hypothesis) Test Statistic for Testing a Claim about a Proportion z= p-p pq n Traditional Method Same as described in Sections 7-2 and 7-3 and in Figure 7-5 P-Value Method Same as described in Section 7-3 and Figure 7-8 Reject the null hypothesis if the P-value is less than or equal to the significance level . p sometimes is given directly “10% of the observed sports cars are red” is expressed as p = 0.10 p sometimes is given directly “10% of the observed sports cars are red” is expressed as p = 0.10 p sometimes must be calculated “96 surveyed households have cable TV and 54 do not” is calculated using p x 96 =n = = 0.64 (96+54) (determining the sample proportion of households with cable TV) CAUTION CAUTION When the calculation of p results in a decimal with many places, store the number on your calculator and use all the decimals when evaluating the z test statistic. CAUTION When the calculation of p results in a decimal with many places, store the number on your calculator and use all the decimals when evaluating the z test statistic. Large errors can result from rounding p too much. Test Statistic for Testing a Claim about a Proportion z= x-µ z = s = p-p pq n x - np npq = x n np n npq n = p-p pq n ELEMENTARY Section 7-6 STATISTICS Testing a Claim about a Standard Deviation or Variance MARIO F. TRIOLA EIGHTH EDITION Assumptions for testing claims about a population standard deviation or variance 1) The sample is a simple random sample. 2) The population has values that are normally distributed (a strict requirement). Chi-Square Distribution Test Statistic X2= (n - 1) s 2 s2 Chi-Square Distribution Test Statistic X2= n (n - 1) s 2 s2 = sample size s 2 = sample variance s2 = population variance (given in null hypothesis) Critical Values for Chi-Square Distribution Found in Table A-4 Degrees of freedom = n -1 Properties of Chi-Square Distribution All values of X2 are nonnegative, and the distribution is not symmetric. There is a different distribution for each number of degrees of freedom. The critical values are found in Table A-4 using n-1 degrees of freedom. Properties of Chi-Square Distribution Properties of the Chi-Square Distribution Not symmetric x2 All values are nonnegative Figure 7-12 Properties of Chi-Square Distribution Chi-Square Distribution for 10 and 20 Degrees of Freedom Properties of the Chi-Square Distribution df = 10 Not symmetric df = 20 x2 All values are nonnegative Figure 7-12 0 5 10 15 20 25 30 35 40 45 Figure 7-13 There is a different distribution for each number of degrees of freedom. Example: Aircraft altimeters have measuring errors with a standard deviation of 43.7 ft. With new production equipment, 81 altimeters measure errors with a standard deviation of 52.3 ft. Use the 0.05 significance level to test the claim that the new altimeters have a standard deviation different from the old value of 43.7 ft. Example: Aircraft altimeters have measuring errors with a standard deviation of 43.7 ft. With new production equipment, 81 altimeters measure errors with a standard deviation of 52.3 ft. Use the 0.05 significance level to test the claim that the new altimeters have a standard deviation different from the old value of 43.7 ft. Claim: s 43.7 H0: s= 43.7 H1: s 43.7 Example: Aircraft altimeters have measuring errors with a standard deviation of 43.7 ft. With new production equipment, 81 altimeters measure errors with a standard deviation of 52.3 ft. Use the 0.05 significance level to test the claim that the new altimeters have a standard deviation different from the old value of 43.7 ft. Claim: s 43.7 H0: s= 43.7 H1: s 43.7 0.025 = 0.05 2 0.025 = 0.025 Example: Aircraft altimeters have measuring errors with a standard deviation of 43.7 ft. With new production equipment, 81 altimeters measure errors with a standard deviation of 52.3 ft. Use the 0.05 significance level to test the claim that the new altimeters have a standard deviation different from the old value of 43.7 ft. Claim: s 43.7 H0: s= 43.7 H1: s 43.7 0.025 = 0.05 2 0.025 106.629 = 0.025 n = 81 df = 80 Table A-4 Example: Aircraft altimeters have measuring errors with a standard deviation of 43.7 ft. With new production equipment, 81 altimeters measure errors with a standard deviation of 52.3 ft. Use the 0.05 significance level to test the claim that the new altimeters have a standard deviation different from the old value of 43.7 ft. Claim: s 43.7 H0: s= 43.7 H1: s 43.7 = 0.05 2 = 0.025 0.975 0.025 0.025 57.153 106.629 n = 81 df = 80 Table A-4 x 2 = (n -1)s2 s 2 = (81 -1) (52.3)2 43.72 114.586 x 2 = (n -1)s2 s 2 = (81 -1) (52.3)2 43.72 114.586 Reject H0 57.153 106.629 x2 = 114.586 x 2 = (n -1)s2 s 2 = (81 -1) (52.3)2 43.72 114.586 Reject H0 57.153 106.629 x2 = 114.586 The sample evidence supports the claim that the standard deviation is different from 43.7 ft. x 2 = (n -1)s2 s 2 = (81 -1) (52.3)2 43.72 114.586 Reject H0 57.153 106.629 x2 = 114.586 The new production method appears to be worse than the old method. The data supports that there is more variation in the error readings than before. P-Value Method Table A-4 includes only selected values of Specific P-values usually cannot be found Use Table to identify limits that contain the P-value Some calculators and computer programs will find exact P-values Figure 7-15 Proportion, Testing a Claim about a Mean, Standard Deviation, or Variance Start Use the Chi-square distribution with x2 = (n -1)s2 s2 St. Dev s or Variance s2 Which parameter does the claim address ? Proportion P Use the normal distribution ˆ z= P-P pq n where Pˆ= x/n Mean (µ) Use the normal distribution with Is n > 30 ? Yes z= x - µx sn (If s Is unknown use s instead.) Figure 7-15 Proportion, Testing a Claim about a Mean, Standard Deviation, or Variance Use the normal distribution with Is n > 30 ? Yes z= x - µx s n (If s is unknown use s instead.) No Is the distribution of the population essentially normal ? (Use a histogram.) No Use nonparametric methods which don’t require a normal distribution. See Chapter 13. Yes Use the normal distribution with Is s known ? Yes z= x - µx sn (This case is rare.) No Use the Student t distribution with t= x - µx sn ELEMENTARY Chapter 8 MARIO F. TRIOLA STATISTICS Inferences from Two Samples EIGHTH EDITION Chapter 8 Inferences from Two Samples 8-1 Overview 8-2 Inferences about Two Means: Independent and Large Samples 8-3 Inferences about Two Means: Matched Pairs 8-4 Inferences about Two Proportions 8-5 Comparing Variation in Two Samples 8-6 Inferences about Two Means: Independent and Small Samples 8-1 Overview There are many important and meaningful situations in which it becomes necessary to compare two sets of sample data. 8-2 Inferences about Two Means: Independent and Large Samples Definitions Two Samples: Independent The sample values selected from one population are not related or somehow paired with the sample values selected from the other population. If the values in one sample are related to the values in the other sample, the samples are dependent. Such samples are often referred to as matched pairs or paired samples. Assumptions 1. The two samples are independent. 2. The two sample sizes are large. That is, n1 > 30 and n2 > 30. 3. Both samples are simple random samples. Hypothesis Tests Test Statistic for Two Means: Independent and Large Samples Hypothesis Tests Test Statistic for Two Means: Independent and Large Samples z = (x1 - x2) - (µ1 - µ2) s 2. 1 n1 s 2 2 + n 2 Hypothesis Tests Test Statistic for Two Means: Independent and Large Samples s and s If s and s are not known, use s1 and s2 in their places. provided that both samples are large. P-value: Use the computed value of the test statistic z, and find the P-value by following the same procedure summarized in Figure 7-8. Critical values: Based on the significance level , find critical values by using the procedures introduced in Section 7-2. Coke Versus Pepsi Data Set 1 in Appendix B includes the weights (in pounds) of samples of regular Coke and regular Pepsi. Sample statistics are shown. Use the 0.01 significance level to test the claim that the mean weight of regular Coke is different from the mean weight of regular Pepsi. Coke Versus Pepsi Data Set 1 in Appendix B includes the weights (in pounds) of samples of regular Coke and regular Pepsi. Sample statistics are shown. Use the 0.01 significance level to test the claim that the mean weight of regular Coke is different from the mean weight of regular Pepsi. Regular Coke Regular Pepsi n 36 36 x 0.81682 0.82410 s 0.007507 0.005701 Coke Versus Pepsi Coke Versus Pepsi Claim: m1 m2 Ho : m 1 = m 2 H1 : m 1 m 2 = 0.01 Reject H0 Z = - 2.575 Fail to reject H0 m1 - m = 0 or Z = 0 Reject H0 Z = 2.575 Coke Versus Pepsi Test Statistic for Two Means: Independent and Large Samples z = (x1 - x2) - (µ1 - µ2) s 2. 1 n1 s 2 2 + n 2 Coke Versus Pepsi Test Statistic for Two Means: Independent and Large Samples z = (0.81682 - 0.82410) - 0 0.0075707 2 36 = - 4.63 + 0.005701 2 36 Coke Versus Pepsi Claim: m1 m2 Ho : m 1 = m 2 H1 : m 1 m 2 = 0.01 Reject H0 sample data: z = - 4.63 Z = - 2.575 Fail to reject H0 m1 - m = 0 or Z = 0 Reject H0 Z = 2.575 Coke Versus Pepsi Claim: m1 m2 Ho : m 1 = m 2 H1 : m 1 m 2 There is significant evidence to support the claim that there is a difference between the mean weight of Coke and the mean weight of Pepsi. = 0.01 Reject H0 Fail to reject H0 Reject H0 Reject Null sample data: z = - 4.63 Z = - 2.575 m1 - m = 0 or Z = 0 Z = 2.575 Confidence Intervals Confidence Intervals (x1 - x2) - E < (µ1 - µ2) < (x1 - x2) + E Confidence Intervals (x1 - x2) - E < (µ1 - µ2) < (x1 - x2) + E where E = z s 2 1 n1 s 2 2 + n 2 ELEMENTARY Section 8-3 STATISTICS Inferences about Two Means: Matched Pairs MARIO F. TRIOLA EIGHTH EDITION Assumptions 1. The sample data consist of matched pairs. 2. The samples are simple random samples. 3. If the number of pairs of sample data is small (n 30), then the population of differences in the paired values must be approximately normally distributed. Notation for Matched Pairs µd = mean value of the differences d for the population of paired data Notation for Matched Pairs µd = mean value of the differences d for the population of paired data d = mean value of the differences d for the paired sample data (equal to the mean of the x - y values) sd = standard deviation of the differences d for the paired sample data n = number of pairs of data. Test Statistic for Matched Pairs of Sample Data Test Statistic for Matched Pairs of Sample Data t= d - µd sd n where degrees of freedom = n - 1 Critical Values If n 30, critical values are found in Table A-3 (t-distribution). If n > 30, critical values are found in Table A- 2 (normal distribution). Confidence Intervals Confidence Intervals d - E < µd < d + E Confidence Intervals d - E < µd < d + E where E = t/2 sd n degrees of freedom = n -1 How Much Do Male Statistics Students Exaggerate Their Heights? Using the sample data from Table 8-1 with the outlier excluded, construct a 95% confidence interval estimate of md, which is the mean of the differences between reported heights and measured heights of male statistics students. Table 8-1 Reported and Measured Heights (in inches) of Male Statistics Students Student A B C Reported Height 68 74 82.25 D E F G H I J 66.5 69 68 71 70 70 67 K L 68 70 Measured 66.8 73.9 Height 74.3 66.1 67.2 67.9 69.4 69.9 68.6 67.9 67.6 68.8 Difference 1.2 7.95 0.4 0.1 1.6 0.1 outlier 1.8 0.1 1.4 -0.9 0.4 1.2 How Much Do Male Statistics Students Exaggerate Their Heights? d = 0.672727 s = 0.825943 n = 11 t/2 = 2.228 (found from Table A-3 with 10 degrees of freedom and 0.05 in two tails) How Much Do Male Statistics Students Exaggerate Their Heights? E = t/2 sd n E = (2.228)( 0.825943 11 = 0.554841 ) How Much Do Male Statistics Students Exaggerate Their Heights? 0.12 < µd < 1.23 In the long run, 95% o f such samples will lead to confidence intervals that actually do contain the true population mean of the differences. Since the interval does not contain 0, the true value of µd is significantly different from 0. There is sufficient evidence to support the claim that there is a difference between the reported heights and the measured heights of male statistics students. ELEMENTARY STATISTICS Section 8-4 Inferences about Two Proportions MARIO F. TRIOLA EIGHTH EDITION Inferences about Two Proportions Assumptions 1. We have proportions from two independent simple random samples. 2. For both samples, the conditions np 5 and nq 5 are satisfied. Notation for Two Proportions For population 1, we let: p1 = population proportion n1 = size of the sample x1 = number of successes in the sample Notation for Two Proportions For population 1, we let: p1 = population proportion n1 = size of the sample x1 = number of successes in the sample p^1 = x1/n1 (the sample proportion) Notation for Two Proportions For population 1, we let: p1 = population proportion n1 = size of the sample x1 = number of successes in the sample p^1 = x1/n1 (the sample proportion) q^1 = 1 - p^1 Notation for Two Proportions For population 1, we let: p1 = population proportion n1 = size of the sample x1 = number of successes in the sample p^1 = x1/n1 (the sample proportion) q^1 = 1 - p^1 The corresponding meanings are attached ^ . and q^ , which come from to p2, n2 , x2 , p 2 2 population 2. Pooled Estimate of p1 and p2 The pooled estimate of p1 and p2 is denoted by p Pooled Estimate of p1 and p2 The pooled estimate of p1 and p2 is denoted by p x1 + x2 p= n +n 1 2 Pooled Estimate of p1 and p2 The pooled estimate of p1 and p2 is denoted by p x1 + x2 p= n +n 1 2 q =1- p Test Statistic for Two Proportions For H0: p1 = p2 , H0: p1 p2 , H1: p1 p2 , H0: p1 p2 H1: p1 < p2 , H1: p 1> p2 Test Statistic for Two Proportions For H0: p1 = p2 , H0: p1 p2 , H1: p1 p2 , z= H0: p1 p2 H1: p1 < p2 , H1: p 1> p2 ( p^1 - p^2 ) ( p1 - p2 ) pq pq + n2 n1 Test Statistic for Two Proportions For H0: p1 = p2 , H0: p1 p2 , where H0: p1 p2 H1: p1 p2 , H1: p1 < p2 , H1: p 1> p2 p1 - p 2 = 0 (assumed in the null hypothesis) Test Statistic for Two Proportions For H0: p1 = p2 , H0: p1 p2 , H0: p1 p2 H1: p1 p2 , H1: p1 < p2 , H1: p 1> p2 p1 - p 2 = 0 (assumed in the null hypothesis) where p^ 1 p= x1 + x2 n1 + n2 x1 = n 1 and and p^ 2 x2 = n2 q=1-p Confidence Interval Estimate of p1 - p2 (p^1 - p^2 ) - E < ( p1 - p2 ) < (p^1 - p^2 ) + E Confidence Interval Estimate of p1 - p2 (p^1 - p^2 ) - E < ( p1 - p2 ) < (p^1 - p^2 ) + E where E = z p^1 q^1 p^2 q^2 n1 + n2 STATISTICS ELEMENTARY Chapter 9 Correlation and Regression MARIO F. TRIOLA EIGHTH EDITION Chapter 9 Correlation and Regression 9-1 Overview 9-2 Correlation 9-3 Regression 9-4 Variation and Prediction Intervals 9-5 Multiple Regression 9-6 Modeling 9-1 Overview Paired Data is there a relationship if so, what is the equation use the equation for prediction 9-2 Correlation Definition Correlation exists between two variables when one of them is related to the other in some way Assumptions 1. The sample of paired data (x,y) is a random sample. 2. The pairs of (x,y) data have a bivariate normal distribution. Definition Scatterplot (or scatter diagram) is a graph in which the paired (x,y) sample data are plotted with a horizontal x axis and a vertical y axis. Each individual (x,y) pair is plotted as a single point. Scatter Diagram of Paired Data Scatter Diagram of Paired Data Positive Linear Correlation y y y (a) Positive Figure 9-1 x x x (b) Strong positive Scatter Plots (c) Perfect positive Negative Linear Correlation y y y (d) Negative Figure 9-1 x x x (e) Strong negative Scatter Plots (f) Perfect negative No Linear Correlation y y x (g) No Correlation Figure 9-1 Scatter Plots x (h) Nonlinear Correlation Definition Linear Correlation Coefficient r measures strength of the linear relationship between paired x and y values in a sample Definition Linear Correlation Coefficient r measures strength of the linear relationship between paired x and y values in a sample nxy - (x)(y) r= Formula 9-1 n(x2) - (x)2 n(y2) - (y)2 Definition Linear Correlation Coefficient r measures strength of the linear relationship between paired x and y values in a sample nxy - (x)(y) r= n(x2) - (x)2 n(y2) - (y)2 Formula 9-1 Calculators can compute r (rho) is the linear correlation coefficient for all paired data in the population. Notation for the Linear Correlation Coefficient n = number of pairs of data presented denotes the addition of the items indicated. x denotes the sum of all x values. x2 indicates that each x score should be squared and then those squares added. (x)2 indicates that the x scores should be added and the total then squared. xy indicates that each x score should be first multiplied by its corresponding y score. After obtaining all such products, find their sum. r represents linear correlation coefficient for a sample represents linear correlation coefficient for a population Rounding the Linear Correlation Coefficient r Round to three decimal places so that it can be compared to critical values in Table A-6 Use calculator or computer if possible Interpreting the Linear Correlation Coefficient If the absolute value of r exceeds the value in Table A - 6, conclude that there is a significant linear correlation. Otherwise, there is not sufficient evidence to support the conclusion of significant linear correlation. TABLE A-6 Critical Values of the Pearson Correlation Coefficient r n 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 45 50 60 70 80 90 100 = .05 .950 .878 .811 .754 .707 .666 .632 .602 .576 .553 .532 .514 .497 .482 .468 .456 .444 .396 .361 .335 .312 .294 .279 .254 .236 .220 .207 .196 = .01 .999 .959 .917 .875 .834 .798 .765 .735 .708 .684 .661 .641 .623 .606 .590 .575 .561 .505 .463 .430 .402 .378 .361 .330 .305 .286 .269 .256 Properties of the Linear Correlation Coefficient r 1. -1 r 1 2. Value of r does not change if all values of either variable are converted to a different scale. 3. The r is not affected by the choice of x and y. Interchange x and y and the value of r will not change. 4. r measures strength of a linear relationship. Common Errors Involving Correlation 1. Causation: It is wrong to conclude that correlation implies causality. 2. Averages: Averages suppress individual variation and may inflate the correlation coefficient. 3. Linearity: There may be some relationship between x and y even when there is no significant linear correlation. Common Errors Involving Correlation FIGURE 9-2 250 Distance (feet) 200 150 100 50 0 0 1 2 3 4 5 6 7 8 Time (seconds) Scatterplot of Distance above Ground and Time for Object Thrown Upward Formal Hypothesis Test To determine whether there is a significant linear correlation between two variables Two methods Both methods let H0: = (no significant linear correlation) H1: (significant linear correlation) Method 1: Test Statistic is t (follows format of earlier chapters) Test statistic: t= r 1-r2 n-2 Method 1: Test Statistic is t (follows format of earlier chapters) Test statistic: t= r 1-r2 n-2 Critical values: use Table A-3 with degrees of freedom = n - 2 Method 1: Test Statistic is t (follows format of earlier chapters) Figure 9-4 Method 2: Test Statistic is r (uses fewer calculations) Test statistic: r Critical values: Refer to Table A-6 (no degrees of freedom) Method 2: Test Statistic is r (uses fewer calculations) Test statistic: r Critical values: Refer to Table A-6 (no degrees of freedom) Reject =0 -1 Figure 9-5 Fail to reject =0 r = - 0.811 0 Reject =0 r = 0.811 Sample data: r = 0.828 1 FIGURE 9-3 Start Testing for a Linear Correlation Let H0: = 0 H1: 0 Select a significance level Calculate r using Formula 9-1 METHOD 1 METHOD 2 The test statistic is t= The test statistic is r r Critical values of t are from Table A-6 1-r2 n -2 Critical values of t are from Table A-3 with n -2 degrees of freedom If the absolute value of the test statistic exceeds the critical values, reject H0: = 0 Otherwise fail to reject H0 If H0 is rejected conclude that there is a significant linear correlation. If you fail to reject H0, then there is not sufficient evidence to conclude that there is linear correlation. Is there a significant linear correlation? Data from the Garbage Project x Plastic (lb) 0.27 1.41 2.19 2.83 2.19 1.81 0.85 3.05 y Household 2 3 3 6 4 2 1 5 Is there a significant linear correlation? Data from the Garbage Project x Plastic (lb) 0.27 1.41 2.19 2.83 2.19 1.81 0.85 3.05 y Household 2 3 3 6 4 2 1 5 n=8 = 0.05 =0 H : 0 H0: 1 Test statistic is r = 0.842 Is there a significant linear correlation? n=8 = 0.05 =0 H : 0 H0: 1 Test statistic is r = 0.842 Critical values are r = - 0.707 and 0.707 (Table A-6 with n = 8 and = 0.05) TABLE A-6 Critical Values of the Pearson Correlation Coefficient r n 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 45 50 60 70 80 90 100 = .05 .950 .878 .811 .754 .707 .666 .632 .602 .576 .553 .532 .514 .497 .482 .468 .456 .444 .396 .361 .335 .312 .294 .279 .254 .236 .220 .207 .196 = .01 .999 .959 .917 .875 .834 .798 .765 .735 .708 .684 .661 .641 .623 .606 .590 .575 .561 .505 .463 .430 .402 .378 .361 .330 .305 .286 .269 .256 Is there a significant linear correlation? Reject =0 -1 r = - 0.707 Fail to reject =0 0 Reject =0 r = 0.707 Sample data: r = 0.842 1 Is there a significant linear correlation? 0.842 > 0.707, That is the test statistic does fall within the critical region. Reject =0 -1 r = - 0.707 Fail to reject =0 0 Reject =0 r = 0.707 Sample data: r = 0.842 1 Is there a significant linear correlation? 0.842 > 0.707, That is the test statistic does fall within the critical region. Therefore, we REJECT H0: = 0 (no correlation) and conclude there is a significant linear correlation between the weights of discarded plastic and household size. Reject =0 -1 r = - 0.707 Fail to reject =0 0 Reject =0 r = 0.707 Sample data: r = 0.842 1 Justification for r Formula Justification for r Formula Formula 9-1 is developed from r= (x -x) (y -y) (n -1) Sx Sy Justification for r Formula Formula 9-1 is developed from r= (x -x) (y -y) (n -1) Sx Sy (x, y) centroid of sample points Justification for r Formula Formula 9-1 is developed from r= (x -x) (y -y) (x, y) (n -1) Sx Sy centroid of sample points x=3 y x - x = 7- 3 = 4 (7, 23) • 24 20 y - y = 23 - 11 = 12 Quadrant 1 Quadrant 2 16 • 12 8 • Quadrant 3 •• 4 y = 11 (x, y) Quadrant 4 FIGURE 9-6 x 0 0 1 2 3 4 5 6 7 ELEMENTARY STATISTICS Section 9-3 Regression MARIO F. TRIOLA EIGHTH EDITION Regression Definition Regression Equation Regression Definition Regression Equation Given a collection of paired data, the regression equation Regression Definition Regression Equation Given a collection of paired data, the regression equation y^ = b0 + b1x algebraically describes the relationship between the two variables Regression Definition Regression Equation Given a collection of paired data, the regression equation y^ = b0 + b1x algebraically describes the relationship between the two variables Regression Line (line of best fit or least-squares line) Regression Definition Regression Equation Given a collection of paired data, the regression equation y^ = b0 + b1x algebraically describes the relationship between the two variables Regression Line (line of best fit or least-squares line) the graph of the regression equation Regression Line Plotted on Scatter Plot The Regression Equation x is the independent variable (predictor variable) The Regression Equation x is the independent variable (predictor variable) ^y is the dependent variable (response variable) The Regression Equation x is the independent variable (predictor variable) ^y is the dependent variable (response variable) y^ = b0 +b1x y = mx +b The Regression Equation x is the independent variable (predictor variable) ^y is the dependent variable (response variable) y^ = b0 +b1x b0 = y - intercept y = mx +b b1 = slope Notation for Regression Equation Notation for Regression Equation Population Parameter y-intercept of regression equation Slope of regression equation Equation of the regression line Sample Statistic 0 b0 1 b1 y = 0 + 1 x ^y = b + b x 0 1 Assumptions 1. We are investigating only linear relationships. 2. For each x value, y is a random variable having a normal (bell-shaped) distribution. All of these y distributions have the same variance. Also, for a given value of x, the distribution of y-values has a mean that lies on the regression line. (Results are not seriously affected if departures from normal distributions and equal variances are not too extreme.) Formula for b0 and b1 Formula for b0 and b1 Formula 9-2 b0 = (y) (x2) - (x) (xy) n(x2) - (x)2 (y-intercept) Formula for b0 and b1 Formula 9-2 Formula 9-3 b0 = b1 = (y) (x2) - (x) (xy) n(x2) - (x)2 n(xy) - (x) (y) n(x2) - (x)2 (y-intercept) (slope) Formula for b0 and b1 Formula 9-2 Formula 9-3 b0 = b1 = (y) (x2) - (x) (xy) n(x2) - (x)2 n(xy) - (x) (y) n(x2) - (x)2 (y-intercept) (slope) calculators or computers can compute these values If you find b1 first, then If you find b1 first, then b0 = y - b1x Formula 9-4 If you find b1 first, then b0 = y - b1x Formula 9-4 Can be used for Formula 9-2, where y is the mean of the y-values and x is the mean of the x values The regression line fits the sample points best. Rounding the y-intercept b0 and the slope b1 Round to three significant digits If you use the formulas 9-2 and 9-3, try not to round intermediate values. Predictions In predicting a value of y based on some given value of x ... 1. If there is not a significant linear correlation, the best predicted y-value is y. Predictions In predicting a value of y based on some given value of x ... 1. If there is not a significant linear correlation, the best predicted y-value is y. 2. If there is a significant linear correlation, the best predicted y-value is found by substituting the x-value into the regression equation. FIGURE 9-7 Predicting the Value of a Variable Start Calculate the value of r and test the hypothesis that = 0 Is there a significant linear correlation ? Yes No Given any value of one variable, the best predicted value of the other variable is its sample mean. Use the regression equation to make predictions. Substitute the given value in the regression equation. Guidelines for Using The Regression Equation 1. If there is no significant linear correlation, don’t use the regression equation to make predictions. 2. When using the regression equation for predictions, stay within the scope of the available sample data. 3. A regression equation based on old data is not necessarily valid now. 4. Don’t make predictions about a population that is different from the population from which the sample data was drawn. What is the best predicted size of a household that discard 0.50 lb of plastic? Data from the Garbage Project x Plastic (lb) y Household 0.27 1.41 2 3 2.19 2.83 2.19 1.81 0.85 3.05 3 6 4 2 1 5 What is the best predicted size of a household that discard 0.50 lb of plastic? Data from the Garbage Project x Plastic (lb) y Household 0.27 1.41 2 3 2.19 2.83 2.19 1.81 0.85 3.05 3 6 4 2 1 5 Using a calculator: b0 = 0.549 b1= 1.48 y = 0.549 + 1.48x What is the best predicted size of a household that discard 0.50 lb of plastic? Data from the Garbage Project x Plastic (lb) y Household 0.27 1.41 2 3 2.19 2.83 2.19 1.81 0.85 3.05 3 6 4 2 1 5 Using a calculator: b0 = 0.549 b1= 1.48 Because there is a significant linear correlation, the equation can be used for prediction. y = 0.549 + 1.48 (0.50) y = 1.3 What is the best predicted size of a household that discard 0.50 lb of plastic? Data from the Garbage Project x Plastic (lb) y Household 0.27 1.41 2 3 2.19 2.83 2.19 1.81 0.85 3.05 3 6 4 2 1 5 Using a calculator: b0 = 0.549 b1= 1.48 y = 0.549 + 1.48 (0.50) y = 1.3 A household that discards 0.50 lb of plastic has approximately one person. Definitions Marginal Change the amount a variable changes when the other variable changes by exactly one unit Outlier a point lying far away from the other data points Influential Points points which strongly affect the graph of the regression line Residuals and the Least-Squares Property Definitions Residuals and the Least-Squares Property Definitions Residual for a sample of paired (x,y) data, the difference (y - ^ y) ^ between an observed sample y-value and the value of y, which is the value of y that is predicted by using the regression equation. Residuals and the Least-Squares Property Definitions Residual for a sample of paired (x,y) data, the difference (y - ^ y) ^ between an observed sample y-value and the value of y, which is the value of y that is predicted by using the regression equation. Least-Squares Property A straight line satisfies this property if the sum of the squares of the residuals is the smallest sum possible. Residuals and the Least-Squares Property x y 1 2 4 24 4 5 8 32 Residuals and the Least-Squares Property x y 1 2 4 24 ^ y = 5 + 4x 4 5 8 32 y 32 30 28 26 24 22 20 18 16 14 12 10 8 6 4 2 0 FIGURE 9-8 • Residual = 7 • Residual = 11 • • Residual = -13 Residual = -5 x 1 2 3 4 5 ELEMENTARY Section 9-4 STATISTICS Variation and Prediction Intervals MARIO F. TRIOLA EIGHTH EDITION Definitions Definitions Total Deviation from the mean of the particular point (x, y) the vertical distance y - y, which is the distance between the point (x, y) and the horizontal line passing through the sample mean y Definitions Total Deviation from the mean of the particular point (x, y) the vertical distance y - y, which is the distance between the point (x, y) and the horizontal line passing through the sample mean y Explained Deviation the vertical distance y^ - y, which is the distance between the predicted y value and the horizontal line passing through the sample mean y Definitions Total Deviation from the mean of the particular point (x, y) the vertical distance y - y, which is the distance between the point (x, y) and the horizontal line passing through the sample mean y Explained Deviation the vertical distance y^ - y, which is the distance between the predicted y value and the horizontal line passing through the sample mean y Unexplained Deviation the vertical distance y - ^ y, which is the vertical distance between the point (x, y) and the regression line. (The distance y - ^y is also called a residual, as defined in Section 9-3.) Figure 9-9 Unexplained, Explained, and Total Deviation Figure 9-9 Unexplained, Explained, and Total Deviation y 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 (5, 19) • Total deviation (y - y ) Unexplained deviation ^) (y - y (5, 13) • Explained deviation (^ y - y) • y=9 (5, 9) y^ = 3 + 2x x 0 1 2 3 4 5 6 7 8 9 (total deviation) = (explained deviation) + (unexplained deviation) ^ ^ (y - y) = (y - y) + (y - y) (total deviation) = (explained deviation) + (unexplained deviation) ^ ^ (y - y) = (y - y) + (y - y) (total variation) = (explained variation) + (unexplained variation) 2 (y - y) = ^ (y - y) Formula 9-5 2 + ^ (y - y) 2 Definition Coefficient of determination the amount of the variation in y that is explained by the regression line Definition Coefficient of determination the amount of the variation in y that is explained by the regression line r 2 = explained variation total variation Definition Coefficient of determination the amount of the variation in y that is explained by the regression line r 2 = explained variation. total variation or simply square r (determined by Formula 9-1, section 9-2) Prediction Intervals Definition Standard error of estimate Prediction Intervals Definition Standard error of estimate a measure of the differences (or distances) between the observed sample y values and the predicted values y^ that are obtained using the regression equation Standard Error of Estimate Standard Error of Estimate s (y e = n-2 2 ^ - y) Standard Error of Estimate (y s e = 2 ^ - y) n-2 or s e = y 2 - b0 n-2 y - b1 xy Formula 9-6 Prediction Interval for an Individual y Prediction Interval for an Individual y y^ - E < y < ^y + E Prediction Interval for an Individual y y^ - E < y < ^y + E where E=t 1 n(x0 - x) 2 1+ n + 2 2 s 2 e n( x ) - ( x) Prediction Interval for an Individual y y^ - E < y < ^y + E where E=t 1 n(x0 - x) 2 1+ n + 2 2 s 2 e n( x ) - ( x) x0 represents the given value of x t 2 has n - 2 degrees of freedom ELEMENTARY Chapter 10 MARIO F. TRIOLA STATISTICS Multinomial Experiments and Contingency Tables EIGHTH EDITION Chapter 10 Multinomial Experiments and Contingency Tables 10-1 Overview 10-2 Multinomial Experiments: Goodness-of-fit 10-3 Contingency Tables: Independence and Homogeneity 10-1 Overview Focus on analysis of categorical (qualitative or attribute) data that can be separated into different categories (often called cells) Use the X2 (chi-square) test statistic (Table A-4) One-way frequency table (single row or column) Two-way frequency table or contingency table (two or more rows and columns) 10-2 Multinomial Experiments: Goodness-of-Fit Assumptions when testing hypothesis that the population proportion for each of the categories is as claimed: 1. The data have been randomly selected. 2. The sample data consist of frequency counts for each of the different categories. 3. The expected frequency is at least 5. (There is no requirement that the observed frequency for each category must be at least 5.) Definition Multinomial Experiment An experiment that meets the following conditions: 1. The number of trials is fixed. 2. The trials are independent. 3. All outcomes of each trial must be classified into exactly one of several different categories. 4. The probabilities for the different categories remain constant for each trial. Definition Goodness-of-fit test used to test the hypothesis that an observed frequency distribution fits (or conforms to) some claimed distribution Goodness-of-Fit Test Notation 0 represents the observed frequency of an outcome E represents the expected frequency of an outcome k represents the number of different categories or outcomes n represents the total number of trials Expected Frequencies If all expected frequencies are equal: E= n k the sum of all observed frequencies divided by the number of categories Expected Frequencies If all expected frequencies are not all equal: E=np each expected frequency is found by multiplying the sum of all observed frequencies by the probability for the category Goodness-of-fit Test in Multinomial Experiments Test Statistic X = 2 (O - E)2 E Critical Values 1. Found in Table A-4 using k-1 degrees of freedom where k = number of categories 2. Goodness-of-fit hypothesis tests are always right-tailed. A close agreement between observed and expected values will lead to a small value of X2 and a large P-value. A large disagreement between observed and expected values will lead to a large value of X2 and a small P-value. A significantly large value of will cause a rejection of the null hypothesis of no difference between the observed and the expected. 2 Relationships Among Components in Goodness-of-Fit Hypothesis Test Figure 10-3 Categories with Equal Frequencies (Probabilities) H0: p1 = p2 = p3 = . . . = pk H1: at least one of the probabilities is different from the others Categories with Unequal Frequencies (Probabilities) H0: p1 , p2, p3, . . . , pk are as claimed H1: at least one of the above proportions is different from the claimed value Example: Mars, Inc. claims its M&M candies are distributed with the color percentages of 30% brown, 20% yellow, 20% red, 10% orange, 10% green, and 10% blue. At the 0.05 significance level, test the claim that the color distribution is as claimed by Mars, Inc. Example: Mars, Inc. claims its M&M candies are distributed with the color percentages of 30% brown, 20% yellow, 20% red, 10% orange, 10% green, and 10% blue. At the 0.05 significance level, test the claim that the color distribution is as claimed by Mars, Inc. Claim: p1 = 0.30, p2 = 0.20, p3 = 0.20, p4 = 0.10, p5 = 0.10, p6 = 0.10 H0 : p1 = 0.30, p2 = 0.20, p3 = 0.20, p4 = 0.10, p5 = 0.10, p6 = 0.10 H1: At least one of the proportions is different from the claimed value. Example: Mars, Inc. claims its M&M candies are distributed with the color percentages of 30% brown, 20% yellow, 20% red, 10% orange, 10% green, and 10% blue. At the 0.05 significance level, test the claim that the color distribution is as claimed by Mars, Inc. Frequencies of M&Ms Brown Yellow Red Orange Green Blue Observed frequency n = 100 33 26 21 8 7 5 Example: Mars, Inc. claims its M&M candies are distributed with the color percentages of 30% brown, 20% yellow, 20% red, 10% orange, 10% green, and 10% blue. At the 0.05 significance level, test the claim that the color distribution is as claimed by Mars, Inc. Frequencies of M&Ms Brown Yellow Red Orange Green Blue Observed frequency n = 100 33 26 21 8 7 Brown E = np = (100)(0.30) = 30 Yellow E = np = (100)(0.20) = 20 Red E = np = (100)(0.20) = 20 Orange E = np = (100)(0.10) = 10 Green E = np = (100)(0.10) = 10 Blue E = np = (100)(0.10) = 10 5 Frequencies of M&Ms Brown Yellow Red Orange Green Blue Observed frequency 33 26 21 8 7 5 Expected frequency 30 20 20 10 10 10 0.3 1.8 0.05 0.4 0.9 2.5 (O -E)2/E Frequencies of M&Ms Brown Yellow Red Orange Green Blue Observed frequency 33 26 21 8 7 5 Expected frequency 30 20 20 10 10 10 0.3 1.8 0.05 0.4 0.9 2.5 (O -E)2/E Test Statistic X = 2 (O - E)2 = E 5.95 Frequencies of M&Ms Brown Yellow Red Orange Green Blue Observed frequency 33 26 21 8 7 5 Expected frequency 30 20 20 10 10 10 0.3 1.8 0.05 0.4 0.9 2.5 (O -E)2/E Test Statistic X2 = (O - E)2 = E 2 5.95 Critical Value X =11.071 (with k-1 = 5 and = 0.05) Fail to Reject Reject = 0.05 0 X2 = 11.071 Sample data: X2 = 5.95 Test Statistic does not fall within critical region; Fail to reject H0: percentages are as claimed There is not sufficient evidence to warrant rejection of the claim that the colors are distributed with the given percentages. Comparison of Claimed and Observed Proportions 0.30 • • • • 0.20 Proportions Observed proportions •• Claimed proportions 0.10 • • • • 0 Orange Yellow Brown Red Green • • Blue ELEMENTARY Section 10-3 MARIO F. TRIOLA STATISTICS Contingency Tables: Independence and Homogeneity EIGHTH EDITIO Definition Contingency Table (or two-way frequency table) a table in which frequencies correspond to two variables. (One variable is used to categorize rows, and a second variable is used to categorize columns.) Definition Contingency Table (or two-way frequency table) a table in which frequencies correspond to two variables. (One variable is used to categorize rows, and a second variable is used to categorize columns.) Contingency tables have at least two rows and at least two columns. Definition Test of Independence tests the null hypothesis that the row variable and column variable in a contingency table are not related. (The null hypothesis is the statement that the row and column variables are independent.) Assumptions 1. The sample data are randomly selected. 2. The null hypothesis H0 is the statement that the row and column variables are independent; the alternative hypothesis H1 is the statement that the row and column variables are dependent. 3. For every cell in the contingency table, the expected frequency E is at least 5. (There is no requirement that every observed frequency must be at least 5.) Test of Independence Test Statistic X = 2 (O - E)2 E Critical Values 1. Found in Table A-4 using degrees of freedom = (r - 1)(c - 1) r is the number of rows and c is the number of columns 2. Tests of Independence are always right-tailed. E= (row total) (column total) (grand total) Total number of all observed frequencies in the table Tests of Independence H0: The row variable is independent of the column variable H1: The row variable is dependent (related to) the column variable This procedure cannot be used to establish a direct cause-and-effect link between variables in question. Dependence means only there is a relationship between the two variables. Expected Frequency for Contingency Tables Expected Frequency for Contingency Tables E= grand total • row total grand total • column total grand total Expected Frequency for Contingency Tables E= grand total n • • row total grand total • column total grand total p (probability of a cell) Expected Frequency for Contingency Tables E= grand total n • • row total grand total • column total grand total p (probability of a cell) Expected Frequency for Contingency Tables E= grand total n • • row total grand total • column total grand total p (probability of a cell) E= (row total) (column total) (grand total) Is the type of crime independent of whether the criminal is a stranger? Stranger Acquaintance or Relative Homicide 12 39 Robbery Assault 379 727 106 642 Is the type of crime independent of whether the criminal is a stranger? Stranger Homicide 12 Assault Row Total 379 727 1118 Robbery Acquaintance or Relative 39 106 642 787 Column Total 51 485 1369 1905 Is the type of crime independent of whether the criminal is a stranger? Stranger Homicide 12 Assault Row Total 379 727 1118 Robbery Acquaintance or Relative 39 106 642 787 Column Total 51 485 1369 1905 E= (row total) (column total) (grand total) Is the type of crime independent of whether the criminal is a stranger? Homicide 12 Stranger Assault Row Total 379 727 1118 Robbery (29.93) Acquaintance or Relative 39 106 642 787 Column Total 51 485 1369 1905 E= (row total) (column total) (grand total) E = (1118)(5 = 29.93 1) 1905 Is the type of crime independent of whether the criminal is a stranger? Stranger Acquaintance or Relative Row Total 727 1118 Robbery (29.93) (284.64) (803.43) 39 (21.07) 106 (200.36) 642 (565.57) 787 485 1369 1905 379 51 Column Total E= E Assault Homicide 12 = (1118)(5 1) 1905 (row total) (column total) (grand total) = 29.93 E = (1118)(485)= 284.64 etc. 1905 Is the type of crime independent of whether the criminal is a stranger? X = 2 (O - E )2 E Homicide Stranger Acquaintance 12 (29.93) Robbery Forgery 379 (284.64) 727 (803.43) 106 (200.36) 642 (565.57 [10.741] 39 (21.07) or Relative (O -E )2 Upper left cell: = E (12 -29.93)2 = 10.741 29.93 (E) (O - E )2 E Is the type of crime independent of whether the criminal is a stranger? X = 2 (O - E )2 E Homicide Stranger Acquaintance or Relative 12 (29.93) [10.741] 39 (21.07) [15.258] (O -E )2 Upper left cell: = E Robbery Forgery 379 (284.64) [31.281] 727 (803.43) [7.271] 106 (200.36) [44.439] 642 (565.57) [10.329] (12 -29.93)2 = 10.741 29.93 (E) (O - E )2 E Is the type of crime independent of whether the criminal is a stranger? X = 2 (O - E )2 E Homicide 12 (29.93) Stranger [10.741] Acquaintance or Relative 39 (21.07) [15.258] Robbery Forgery 379 (284.64) [31.281] 727 (803.43) [7.271] 106 (200.36) [44.439] 642 (565.57) [10.329] 2 Test Statistic X = 10.741 + 31.281 + ... + 10.329 = 119.319 (E) (O - E )2 E Test Statistic X2 = 119.319 with = 0.05 and (r -1) (c -1) = (2 -1) (3 -1) = 2 degrees of freedom Critical Value X2 = 5.991 (from Table A-4) Test Statistic X2 = 119.319 with = 0.05 and (r -1) (c -1) = (2 -1) (3 -1) = 2 degrees of freedom Critical Value X2 = 5.991 (from Table A-4) Fail to Reject Independence Reject Independence = 0.05 0 X2 = 5.991 Sample data: X2 =119.319 Test Statistic X2 = 119.319 with = 0.05 and (r -1) (c -1) = (2 -1) (3 -1) = 2 degrees of freedom Critical Value X2 = 5.991 (from Table A-4) Fail to Reject Independence Reject Independence = 0.05 0 X2 = 5.991 Reject independence Sample data: X2 =119.319 Test Statistic X2 = 119.319 with = 0.05 and (r -1) (c -1) = (2 -1) (3 -1) = 2 degrees of freedom Critical Value X2 = 5.991 (from Table A-4) Fail to Reject Independence Reject Independence = 0.05 0 X2 = 5.991 Reject independence Sample data: X2 =119.319 Claim: The type of crime and knowledge of criminal are independent Ho : The type of crime and knowledge of criminal are independent H1 : The type of crime and knowledge of criminal are dependent Test Statistic X2 = 119.319 with = 0.05 and (r -1) (c -1) = (2 -1) (3 -1) = 2 degrees of freedom Critical Value X2 = 5.991 (from Table A-4) Fail to Reject Independence Reject Independence = 0.05 0 X2 = 5.991 Reject independence Sample data: X2 =119.319 It appears that the type of crime and knowledge of the criminal are related. Relationships Among Components in X2 Test of Independence Figure 10-8 Definition Test of Homogeneity test the claim that different populations have the same proportions of some characteristics How to distinguish between a test of homogeneity and a test for independence: Were predetermined sample sizes used for different populations (test of homogeneity), or was one big sample drawn so both row and column totals were determined randomly (test of independence)? ELEMENTARY Chapter 11 STATISTICS Analysis of Variance MARIO F. TRIOLA EIGHTH EDITION Chapter 11 Analysis of Variance 11-1 Overview 11-2 One-way ANOVA 11-3 Two-way ANOVA 11-1 Overview An introduction of a procedure for testing the hypothesis that three or more population means are equal. For example: H0 : µ 1 = µ2 = µ3 = . . . µk H1: At least one mean is different 11-1 Overview Definition Analysis of Variance (ANOVA) a method of testing the equality of three or more population means by analyzing sample variations ANOVA methods require the F-distribution 1. The F-distribution is not symmetric; it is skewed to the right. 2. The values of F can be 0 or positive, they cannot be negative. 3. There is a different F-distribution for each pair of degrees of freedom for the numerator and denominator. Critical values of F are given in Table A-5 F - distribution Not symmetric (skewed to the right) nonnegative values only Figure 11-1 11-2 One-Way ANOVA Assumptions 1. The populations have normal distributions. 2. The populations have the same variance s2 (or standard deviation s ). 3. The samples are simple random samples. 4. The samples are independent of each other. 5. The different samples are from populations that are categorized in only one way. Definition Treatment (or factor) a property or characteristic that allows us to distinguish the different populations from another Use computer software or TI-83 Plus for ANOVA calculations if possible Procedure for testing: H0: µ1 = µ2 = µ3 = . . . 1. Use STATDISK, Minitab, Excel, or a TI83 Calulator to obtain results. 2. Identify the P-value from the display. 3. Form a conclusion based on these criteria: If P-value , reject the null hypothesis of equal means. If P-value > , fail to reject the null hypothesis of equal means. Relationships Among Components of ANOVA Figure 11-2 ANOVA Fundamental Concept Estimate the common value of s2 using 1. The variance between samples (also called variation due to treatment) is an estimate of the common population variance s2 that is based on the variability among the sample means. 2. The variance within samples (also called variation due to error) is an estimate of the common population variance s2 based on the sample variances. ANOVA Fundamental Concept Test Statistic for One-Way ANOVA ANOVA Fundamental Concept Test Statistic for One-Way ANOVA F= variance between samples variance within samples ANOVA Fundamental Concept Test Statistic for One-Way ANOVA F= variance between samples variance within samples A excessively large F test statistic is evidence against equal population means. Calculations with Equal Sample Sizes Variance between samples = nsx 2 Calculations with Equal Sample Sizes Variance between samples = nsx 2 2 where sx = variance of samples means Calculations with Equal Sample Sizes Variance between samples = nsx 2 2 where sx = variance of samples means Variance within samples = sp 2 Calculations with Equal Sample Sizes Variance between samples = nsx 2 2 where sx = variance of samples means Variance within samples = sp 2 2 where sp = pooled variance (or the mean of the sample variances) Critical Value of F Right-tailed test Degree of freedom with k samples of the same size n numerator df = k -1 denominator df = k(n -1) Calculations with Unequal Sample Sizes ni(xi - x)2 F= variance within samples variance between samples = k -1 (ni - 1)si 2 (ni - 1) Calculations with Unequal Sample Sizes ni(xi - x)2 F= variance within samples variance between samples = k -1 (ni - 1)si 2 (ni - 1) where x = mean of all sample scores combined Calculations with Unequal Sample Sizes ni(xi - x)2 F= variance within samples variance between samples = k -1 (ni - 1)si 2 (ni - 1) where x = mean of all sample scores combined k = number of population means being compared Calculations with Unequal Sample Sizes ni(xi - x)2 F= variance within samples variance between samples = k -1 (ni - 1)si 2 (ni - 1) where x = mean of all sample scores combined k = number of population means being compared ni = number of values in the ith sample Calculations with Unequal Sample Sizes ni(xi - x)2 F= variance within samples variance between samples = k -1 (ni - 1)si 2 (ni - 1) where x = mean of all sample scores combined k = number of population means being compared ni = number of values in the ith sample xi = mean values in the ith sample Calculations with Unequal Sample Sizes ni(xi - x)2 variance within samples variance between samples F= = k -1 (ni - 1)si 2 (ni - 1) where x = mean of all sample scores combined k = number of population means being compared ni = number of values in the ith sample xi = mean values in the ith sample 2 si = variance of values in the ith sample Key Components of ANOVA Method Key Components of ANOVA Method SS(total), or total sum of squares, is a measure of the total variation (around x) in all the sample data combined. Key Components of ANOVA Method SS(total), or total sum of squares, is a measure of the total variation (around x) in all the sample data combined. SS(total) = (x - x) Formula 11-1 2 Key Components of ANOVA Method SS(treatment) is a measure of the variation between the samples. In one-way ANOVA, SS(treatment) is sometimes referred to as SS(factor). Because it is a measure of variability between the sample means, it is also referred to as SS (between groups) or SS (between samples). Key Components of ANOVA Method SS(treatment) is a measure of the variation between the samples. In one-way ANOVA, SS(treatment) is sometimes referred to as SS(factor). Because it is a measure of variability between the sample means, it is also referred to as SS (between groups) or SS (between samples). SS(treatment) = n1(x1 - x)2 + n2(x2 - x)2 + . . . nk(xk - x)2 Formula 11-2 = ni(xi - x)2 Key Components of ANOVA Method SS(error) is a sum of squares representing the variability that is assumed to be common to all the populations being considered. Key Components of ANOVA Method SS(error) is a sum of squares representing the variability that is assumed to be common to all the populations being considered. 2 1 2 2 2 3 2 i SS(error) = (n1 -1)s + (n2 -1)s + (n3 -1)s . . . nk(xk -1)s = (ni - 1)s Formula 11-3 2 i Key Components of ANOVA Method SS(total) = SS(treatment) + SS(error) Formula 11-4 Mean Squares (MS) Sum of Squares SS(treatment) and SS(error) divided by corresponding number of degrees of freedom. MS (treatment) is mean square for treatment, obtained as follows: Mean Squares (MS) Sum of Squares SS(treatment) and SS(error) divided by corresponding number of degrees of freedom. MS (treatment) is mean square for treatment, obtained as follows: MS (treatment) = Formula 11-5 SS (treatment) k-1 Mean Squares (MS) MS (error) is mean square for error, obtained as follows: Mean Squares (MS) MS (error) is mean square for error, obtained as follows: MS (error) = Formula 11-6 SS (error) N-k Mean Squares (MS) MS (error) is mean square for error, obtained as follows: MS (error) = SS (error) N-k Formula 11-6 MS (total) = Formula 11-7 SS (total) N-1 Test Statistic for ANOVA with Unequal Sample Sizes Test Statistic for ANOVA with Unequal Sample Sizes F= MS (treatment) MS (error) Test Statistic for ANOVA with Unequal Sample Sizes F= MS (treatment) MS (error) Formula 11-8 Numerator df = k -1 Denominator df = N - k