Download Kinematics Multiples

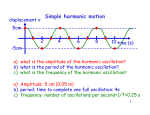
Simple Harmonic Motion
From Princeton Review Book
1. Which of the following is/are characteristics of simple harmonic motion?
I. The acceleration is constant.
II. The restoring force is proportional to the displacement.
III. The frequency is independent of the amplitude.
a. II only.
b. I and II only.
c. I and III only.
d. II and III only.
e. I, II, and III.
* D. I is not true—For example, as the spring compresses in and out, the force and
therefore the acceleration changes. This is why we didn’t use springs in kinematic
problems.
II is true—F = - K(x). Force and displacement are directly proportional.
III is true. The formula for frequency does not have amplitude in it.
The amplitude determines the energy, but not the frequency or period.
2. A block attached to an ideal spring undergoes simple harmonic motion. The
acceleration of the block has its maximum magnitude at the point where:
a. the speed is the maximum.
b. the potential energy is the minimum.
c. the speed is the minimum.
d. the restoring force is the minimum.
e. the kinetic energy is the maximum.
*C. The acceleration is a max. at the turnaround points---this is where the spring is
maximally stretched or compressed and so the pull back to equilibrium is the strongest.
By definition of a turnaround point, this is where the speed is zero.
3. A student measures the maximum speed of a block undergoing simple harmonic
oscillations of amplitude A on the end of an ideal spring. If the block is replaced by one
with twice the mass but the amplitude of its oscillations remains the same, then the
maximum speed of the block will:
a. decrease by a factor of 4.
b. decrease by a factor of 2.
c. decrease by a factor of 2
d. remain the same.
e. increase by a factor of 2.
* C. Compare TME’s when all the energy is kinetic (at the equilibrium) and all of the
energy is stored (at turnarounds):
1
1
2
MVmax
 KA 2
2
2
Solving for V : VMax 
KA 2
m
Thus, doubling the mass would decrease the max speed by a factor of
2
4. A spring-block simple harmonic oscillator is set up so that the oscillations are vertical.
The period of the motion is T. If the spring and block are taken to the surface of the
Moon, where the gravitational acceleration is 1/6 of its value here, then the vertical
oscillations will have a period of:
a. T/6.
b. T/3
c. T / 6
d. T
e. T 6
* D. Trick question. The period of a spring system does not depend on the acceleration
m
due to gravity: T  2
. The period of a PENDULUM would be affected if we took
K
it to the moon.
5. A linear spring of force constant K is used in a physics lab experiment. A block of
mass m is attached to the spring and the resulting frequency, f, of the simple harmonic
oscillations is measured. Blocks of various masses are used in different trials, and in each
case, the corresponding frequency is measured and recorded. If f2 is plotted versus 1/m,
the graph will be a straight line with slope of:
4 2
K2
b.
4 2
K
c. 4 2 K
d.
K
4 2
a.
e.
K2
4 2
* D. Start with the formula for the period of a spring:
m
K
T  2
The frequency is the reciprical of the period, so flip everything :
f 
1
2
f2 
K
m
K
4 m
2
Now, square everything to match what is graphed :
K
Factor out the 1/m, yields : 2
4
6. A simple harmonic oscillator has a frequency of 2.5 Hertz and an amplitude of 0.5 m.
What is the period of the oscillations?
a. 0.2 sec.
b. 0.4 sec.
c. 8 sec.
d. 20 sec.
e. 50 sec.
* B. The amplitude has nothing to do with the period. The period, T, is the reciprocal of
the frequency T = 1/(2.5) = .4 sec.
7. A simple pendulum executes simple harmonic motion as it swings through small
angles of oscillation. If max denotes the amplitude of the oscillations, which of the
following statements is true?
a. When  = 0, the tangential acceleration is zero.
b. When  = max, the tangential acceleration is zero.
c. When  = 0, the speed is zero.
d. When  = 0, the restoring force is maximized.
e. When  = max, the speed is maximized.
*A. The tangential acceleration is caused by the component of weight that is tangent to
the path (as opposed to the centripetal acceleration needed for the pendulum to travel in a
circle). At the bottom of its path, the weight vector is acting radially down, which causes
no acceleration. At any other position, a component of the weight (mgsin ) is acting
tangent to the path, causing the pendulum to speed up or slow down.
8. The figure below shows a linear spring anchored to the
ceiling. If the mass of the block hanging from its lower end
is doubled, what effect will this change have on the block’s
equilibrium position and oscillation period?
a. Equilibrium position: lowered by a factor of 2
Oscillation period: decreased by a factor of 2
b. Equilibrium position: lowered by a factor of 2
Oscillation period: increased by a factor of 2
c. Equilibrium position: lowered by a factor of 2
Oscillation period: increased by a factor of 2
d. Equilibrium position: lowered by a factor of 2
Oscillation period: decreased by a factor of 2
e. Equilibrium position: lowered by a factor of 2
Oscillation period: increased by a factor of 2
* E. The equilibrium position is found using Hooke’s law:
K (X )  mg
Thus, X and m are directly related, so doubling m will lower the equilibriu m by factor of 2
The definition of period for a mass/spring system:
T  2
m
K
Thus, doubling the mass will make the period increase by factor of
2
From Old AP’s
9. A particle oscillates up and down in simple harmonic motion. Its height Y as a function
of time t is shown in the diagram above. At what time t does the particle achieve its
maximum positive acceleration?
a. 1 second.
b. 2 seconds.
c. 3 seconds.
d. 4 seconds.
e. None of the above, because the acceleration is constant.
*A
The acceleration is the second derivative of the graph shown.
So, you are looking for maximum positive concavity which is at t = 1.
You could also sketch the first and second derivative graphs.
You could also remember that since the position function is a negative sine graph, the
second derivative will be a positive sine graph and so when the position is at a max.
negative the second derivative will be at a max. positive.
10. When a mass m is hung on a certain ideal spring, the spring stretches a distance d. If
the mass is then set oscillating on the spring, the period of oscillation is proportional to:
a.
d
g
b.
g
d
c.
d
mg
d.
m2 g
d
e.
m
g
* A. This problem combines two concepts: the formula for period and the definition of
equilibrium for a vertical spring:
m
K
T  2
To find K : use the fact that when a weight of mg hangs on the spring it stretches a distance d :
Thus, the upward force of the spring Kd  mg
so K 
mg
d
Substituti ng this :
m
d
 2
g
 mg 


 d 
T  2
11. A particle moves in a circle in such a way that the X- and Y-coordinates of its motion
are given in meters as functions of time t in seconds by:
X = 5 cos (3t)
Y = 5 sin (3t)
What is the period of revolution of the particle?
a. 1/3 second.
b. 3 seconds.
d.
2
seconds
3
e.
3
seconds
2
f. 6 seconds.
* D.
First off, don’t be confused by the fact that there is an X and a Y function.
Remember the phonograph demo. Whether you just looked at the horizontal or just
looked at the vertical position, either one would oscillate in simple harmonic motion, so
just focus on one.
Remember that the formula for SHO is X = A cos (  t)
So, the rotational speed is 3 radians/sec. We need to “convert” this to the time to
complete one revolution:
 1second  2 radians
T 

 3radians  revolution
 2

 3
12. (1993) Two identical massless springs are hung from a horizontal support. A block of
mass 1.2 kg is suspended from the pair of springs, as shown above. When the block is in
equilibrium, each spring is stretched an additional 0.15 meters. When the block is set into
oscillation with ampltitude A, it passes through its equilibrium point with a speed V. In
which of the following cases will the block, when oscillating with amplitude A, also
have speed V when it passes through its equilibrium point?
I. The block is hung from only one of the two springs.
II. The block is hung from the same two springs, but the springs are connected in
Series rather than in parallel.
III. A 0.5 kg mass is attached to the block.
a. None
b. III only.
c. I and II only.
d. II and III only.
e. I, II, and III.
*A
This is an energy problem. For the speed of the object to remain the same, the same
amount of energy needs to be converted from elastic potential to KE (neglecting the
change in mass, which is an option).
I can’t be true. If you have half the springs, but the same amplitude, there is less stored
energy and the mass will not be going as fast when it passes through equilibrium.
II can’t be true. Putting the springs in parallel will cut the spring constant by a factor of
FOUR, which again means less stored energy.
III is not true. If you reduce the mass but don’t change anything else, you have the same
amount of TME as before, so the block will have the same KE but a faster speed.
13. The displacement vs. time for a particle in simple harmonic motion is shown above.
Which of the following graphs shows the kinetic energy, K, of the particle as a
function of time, t, for one cycle of motion?
a.
b.
c.
d.
e.
*B
First off, you know the KE can never be negative, which throws out graphs A, D, and E.
Second, KE is proportional to velocity squared. So, think about taking the derivative of
the position graph and then squaring it. This means max’s on the position graph become
zeros of the KE graph. This should square with what you know about SHO—max
positions are turnaround points = no KE.
14. A graph of displacement vs. time for a particle in simple harmonic motion is shown
above. Which of the following graphs shows the kinetic energy, K, of the particle as a
function of its displacement x? (careful: the variable on the X-axis has changed!)
a.
b.
c.
d.
e.
* C. The KE must be zero at the turnaround points (max/min positions). The KE is a
maximum at equilibrium (X=0).
15. The length of a simple pendulum with a period on Earth of one second is most
nearly:
a. 0.12 meters.
b. 0.25 meters.
c. 0.50 meters.
d. 1.0 meters.
e. 10.0 meters.
*B.
T  2
L
g
1sec  2(3)
L
10m/s 2
L
1  36 
 10 
L
10 10

 .25
36 40
say 3.14 is about 3
square both sides
Note : if you don' t approximat e anything, the answer is .247
16. A ball is dropped from a height of 10 meters onto a hard surface so that the collision
at the surface may be assumed elastic. Under such conditions the motion of the ball is:
a. simple harmonic with a period of about 1.4 seconds.
b. simple harmonic with a period of about 2.8 seconds.
c. simple harmonic with an amplitude of 5 m.
d. periodic with a period of about 2.8 seconds but not simple harmonic.
e. motion with constant momentum.
* D. The motion is not simple harmonic because the position function of free fall is
parabolic (constant acceleration), not sinusoidal (acceleration that decreases as object
heads towards equilibrium). If you use kinematics to find time to fall you get 1.41
seconds, so the time to return to original position is about 2.82 seconds. The collision
must be elastic or the object will not return to its original position.
Questions 17 and 18:
17. (1984) A 0.1 kg block is attached to an initially unstretched spring of force constant
K= 40 N/m as shown above. The block is released from rest at time t = 0. What is the
amplitude of the resulting simple harmonic motion of the block?
a.
1
m
40
b.
1
m
20
d.
1
m
2
e. 1m
c.
1
m
4
* A. The release point is the top turnaround point. The difference between this point and
equilibrium is the amplitude:
Equilibriu m :
Kx  mg
(40 N / m)( A)  (.1kg)(10m / s 2 )
A
1
m
40
18. (1984) At what time after release will the block first return to its initial position?

a.
s
b.

s
5
e.
40
d.

20
s
c.

s
10

s
4
*C
This is the definition of one full period:
T  2
m
.1kg
1
2 
 2
 2


K
40 N / m
400 20 10
19. (1993) A simple pendulum consists of a 1 kg brass bob on a string about 1.0 meters
long. It has a period of 2.0 seconds. The pendulum would have a period of 1.0 second if
the:
a. string were replaced by one about 0.25 meters long.
b. string were replaced by one about 2.0 meters long.
c. bob were replaced by a .25 kg brass sphere.
d. bob were replaced by a 4.0 kg brass sphere.
e. amplitude of the motion were increased.
*A
They give you a lot of excess information here to trick you. Remember that the period of
a pendulum depends only on its length and the planet it is on. You can check that a
pendulum on Earth of length 1 meter does have a period of about 2 seconds. To cut its
period in HALF, you would need to reduce the length by a factor of FOUR, since it is
under a square root in the period formula.
20. (1984) A simple pendulum of length L, whose bob has mass M, oscillates with a
period T. If the bob is replaced by one of mass 4M, the period of oscillation is:
a. T/4
b. T/2
c. T
d. 2T
e. 4T
*C. Trick question. The period of a pendulum does not depend on mass. The additional
inertia of extra mass is canceled by the additional restoring force of additional weight.
21. Two objects of equal mass hang from independent springs of unequal spring constant
and oscillate up and down. The spring of greater spring constant must have the:
a. smaller amplitude of oscillation.
b. larger amplitude of oscillation.
c. shorter period of oscillation.
d. longer period of oscillation.
e. lower frequency of oscillation.
* C.
Since T  2
m
, If K increases, then T decreases.
K
Logically, the stonger th e pull back to equilibriu m, the shorter th e cycle.
22. (1984) A particle moves in simple harmonic motion represented by the position
function above. Which of the following represents the velocity of the particle as a
function of time?
a. v(t )  4 cos( t )
b. v(t )   cos( t )
c. v(t )  -  2 cos( t )
d. v(t )  - 4 sin(  t)
e. v(t )  - 4  sin(  t)
* E.
Start with by writing the equation for the position function:
 2 
 2 
X  4 cos
t   4cos
t   4cos t 
 T 
 2 
So, V  X   - 4 sin(  t)
23. (1974) The forces produced by two springs as they are stretched are shown in the
graph above. Spring 1 indicated by the dashed line is linear (Hookian), but spring 2 is
not. The period of oscillation for a mass attached to spring 2 is:
a. dependent on amplitude but never greater than for spring 1.
b. dependent on amplitude but never less than for spring 1.
c. dependent on amplitude but always equal to that of spring 1.
d. independent of amplitude and never greater than for spring 1.
e. independent of amplitude and never less than for spring 1.
*A.
This one is tricky. Because the spring is nonlinear, the solution to the differential
equation is not a sine function and the period does depend on the amplitude. If you look
at the graph closely, you will see that the FORCE of spring 2 increases with displacement
faster than the force for spring 1. It should make sense that if the restoring force is
GREATER than it would be for standard simple harmonic motion, the spring will pull the
mass back to equilibrium more quickly, reducing the period.
24. (1974) An object is suspended from a spring whose mass is negligible compared to
that of the object. The object is displaced slightly, and the period of its motion is
observed to be T seconds. The spring is then cut in half and the object is suspended
from one of the halves. The object is displaced slightly and its period is observed to be
T’ seconds. The ratio T’/T is:
a. ½
b.
c. 1
d.
e. 2
*B
1
2
2
m
K
Cutting the spring in half actually DOUBLES the spring constant becuase there are fewer
coils, so less total stretch for a given weig ht.
T  2
T   2
m
2K
So, the ratio is :
T

T
m
2K
m
2
K
2

 
1
2
1

1
2
25.
(2004, 35%)
A 1.0 kg mass is attached to the end of a horizontal ideal spring with a force constant of
400 N/m. The mass is set in simple harmonic motion with an amplitude of 10 cm. The
speed of the 1.0 kg mass at the equilibrium position is:
a. 2 m/s.
b. 4 m/s.
c. 20 m/s.
d. 40 m/s.
e. 200 m/s.
*A.
TME turnaround  TME Equilibrium
KE  U s  KE  U s
0 
1 2
1
Kx  mv 2
2
2
1
1
(400 N / m)(. 1m) 2  (1kg)v 2
2
2
(Don' t forget to convert from cm to m! )
v  2m / s
26.
(2004, 46 %)
A simple pendulum has a period of 2 seconds for small amplitude oscillations.
The length of the pendulum is most nearly:
a. 1/6 meters.
b. ¼ meters.
c. ½ meters.
d. 1 meters.
e. 2 meters.
*D
T  2
2  2
1

1
L
10
L
10

2
L
g

L
10
L
10
2
1
27.
(2004, 28%)
A simple pendulum has a period of 2 seconds for small amplitude oscillations. Which of
the following equations could represent the angle  that the pendulum makes with the
vertical as a function of time, t?
a.    max sin
2 t 
b.    max sin  t 
c.    max sin  2 t 
d.    max sin  4 t 
e.    max sin 8 t 
*B
The formula for simple harmonic motion is:
 2 
X  A sin 
t
 T 
Here, the amplitude is replaced by the maximum angle.
Since the period is 2, the formula becomes opton B
28.
(2004B, 58%)
A block attached to the lower end of a vertical spring oscillates up and down. If the
spring obeys Hooke's law, the period of oscillation depends on which of the following;
I. Mass of the block.
II. Amplitude of the oscillation.
III. Force constant of the spring.
A. I only.
b. II only.
c. III only.
d. I and II.
e. I and III.
* E.
T  2
m
K
A sphere of mass M1, which is attached to a spring, is displaced downward from its
equilibrium position as shown above left and released from rest. A sphere of mass M2,
which is suspended from a string of length L, is displaced to the right as shown above
right and released from rest so that it swings as a simple pendulum with small amplitude.
Assume both spheres undergo simple harmonic motion.
29.
(2004B, 64%)
Which of the following is true for both spheres?
a. The maximum kinetic energy is attained as the sphere passes through its equilibrium
position.
b. The maximum kinetic energy is attained as the sphere reaches its point of release.
c. The minimum gravitational potential energy is attained as the sphere passes through its
equilibrium position.
d. The maximum gravitational potential energy is attained when the sphere reaches its
point of release.
e. The maximum total energy is attained only as the sphere passes through its equilibrium
position.
* A. Maximum speed, and thus maximum KE, always occurs at equilibrium, for both
horizontal and vertical springs and pendula.
30.
(2004B, 34%)
If both spheres have the same period of oscillation, which of the following is an
expression for the spring constant?
a.
L
M1g
b.
g
M 2L
c.
M1L
g
d.
M2g
L
e.
M1g
L
* E.
Set the Periods equal :
T1  T2
2
M1
L
 2
K
g
M1 L

K
g
K
M1g
L