* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Pressure Gradient Force
Jerk (physics) wikipedia , lookup
Classical mechanics wikipedia , lookup
Fundamental interaction wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Equations of motion wikipedia , lookup
Mechanics of planar particle motion wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Seismometer wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Coriolis force wikipedia , lookup
Fictitious force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
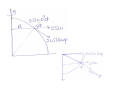
Pressure Gradient Force δV = δxδyδz B δy FBx δz ·C x0,y0,z0 δx A Element of air at C. FAx Due to random molecular motions, momentum is continually imparted to the walls of the volume element by surrounding air. Pressure exerted on the walls of the volume element = momentum transfer per unit time per unit area Pressure at C is p0 By Taylor series pressure on the right wall A 2 ∂p δx 1 ∂ 2p ⎛ δx ⎞ = p0 + + ⎟ +−−−−−− 2 ⎜ ∂x 2 2 ∂x ⎝ 2 ⎠ Keeping upto second term, the force on wall A along x-axis ∂p ∂x ⎞ ⎛ FAx ≈ −⎜ p 0 + ⎟δyδz ∂x 2 ⎠ ⎝ ∂p ∂x ⎞ ⎛ FBx ≈ ⎜ p 0 − ⎟δyδz ∂x 2 ⎠ ⎝ Net x-component force on the volume element Fx = FAx + FBx Fx Similarly Fy FZ ⎡ ⎛ ∂p ∂ x⎤ ∂p ∂x⎞ ⎟⎟ + p 0 − = ⎢− ⎜⎜ p 0 + ⎥δy δz x 2 x 2 ∂ ∂ ⎠ ⎣ ⎝ ⎦ ∂p = - δx δy δz ∂x ∂p = - δx δy δz ∂y ∂p = - δx δy δz ∂z Total pressure gradient force per unit mass F m = (i F x + j Fy + k Fz ) ρ δx δy δz = ⎛ ∂p 1 ∂p ∂p ⎞ 1 = − ∇p − ⎜⎜ i + j + k ⎟⎟ ρ ∂y ∂z ⎠ ρ ⎝ ∂x Hydrostatic equilibrium Let us consider atmospheric/oceanic pressure along with gravity. The decrease in pressure with height in the atmosphere and the increase with depth in the ocean give rise to a vertical pressure gradient force − 1 ∂p where z is the height or depth from the surface ρ ∂z and ρ is the density. The vertical pressure gradient force results in a vertical acceleration in the direction of decreasing pressure i.e. upwards. The vertical pressure gradient force is closely in balance with the downward gravity. 1 ∂p g =− ρ ∂z i.e. This is called hydrostatic (1) balance. This is applicable to most situations in the atmosphere and ocean, except in the case of large vertical accelerations as in thunderstroms. Equation (1) can be integrated and written as − ∫ dp = ∫ ρgdz (2) In the above integration g is usually assumed to be constant. However, g varies with height and latitude due to nonsphericity of earth. Gravitational Force: r Fg r r* GM r ≡ g =− 2 , m r r G = 6.673 ×10 −11 Nm 2 kg − 2 r r* GM r g0 = − 2 a r r* a2 * g = g0 (a + z )2 a = 6.37 ×106 m a Effective Gravity: r r r r g ≡ g +Ω R * 2 r=a+z z Fundamental forces in the atmosphere • Real Forces: Pressure gradient force Gravitational force Frictional force • Apparent Forces: Centrifugal force Coriolis force [An Introduction to Dynamic Met, J.R. Holton Inertial or Newtonian motion Newton’s first law of motion A mass in uniform motion relative to a coordinate system fixed in space will remain in uniform motion in the absence of any forces. Non-Newtonian Motion An object at rest w. r. t. the rotating earth is not at rest or in uniform motion relative to the coordinate system fixed in space. Apparent forces are the inertial reaction terms which arise because of the coordinate acceleration. Centrifugal force For an observer in fixed space, earth rotates with constant speed but there is change in direction and hence velocity is not constant. Ω → constant angular velocity δ v = v δθ δv is directed towards the axis of rotation. dv dθ ⎛⎜ R ⎞⎟ = = v − dt dt ⎜⎝ R ⎟⎠ dθ v = Ω R and =Ω dt δv Lim δ t →0 δt ∴ dv = − Ω 2R dt Ω R Centripetal acceleration Viewed from fixed coordinates, the motion is one of uniform acceleration directed towards the axis of rotation. Coriolis Force: Consider particle moving in the eastward direction. The particle rotates faster than earth. Let u be eastward velocity relative to earth. 2 → Centrifugal force = ⎛⎜ Ω + u ⎞⎟ R R⎠ ⎝ → Ωu → u 2 → 2 R+ 2R =Ω R+2 R R For synoptic motions (horizontal scale of 1000km or so): u p p ΩR Ω = 7.292 x 10 −5 sec −1 , R ≈ a = 6.37 x 10 6 m, u = 10 m / sec 3rd term u 2 → R u R pp 1 = × = → 2 nd term R 2 2 R Ω 2Ωu R Hence 3rd term can be neglected compared to the second. Centrifugal force of a parcel rotating in the eastward direction with relative velocity u → → Ωu = Ω2 R + 2 R R = Centrifugal force of stationary parcel due to rotating earth + Coriolis force.