Download Diony George Stats 1040 TR 1-2:20 Math 1040 Skittles - E

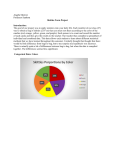
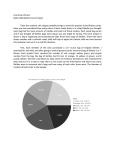
Diony George
Stats 1040 TR 1-2:20
Math 1040 Skittles Term Project
Introduction:
Life is full of questions, and the ways to find the answers are wide and varied. One method is
using the practice of statistics. What is statistics you might ask? The word statistics, according to
Webster’s Dictionary means a “collection of facts representing the state of society, the condition
of the people in a nation or country, their health, longevity, domestic economy, arts, property and
political strength, etc.” Or according to Google, “it’s the practice or science of collecting and
analyzing numerical data in large quantities, especially for the purpose of inferring proportions in
a whole from those in a representative sample.”
The data I’m examining in this project through organizing and analyzing, categorically and
quantitatively, drawing conclusions with confidence intervals and hypothesis testing using the
concepts and tools I’ve learned this semester in Elementary Statistics, is based on a sampling of a
popular chewy candy, colored like the rainbow which was first made commercially in 1974 by a
British Company, and later in the United States in 1982. The overall sample size of 25 bags, 2.17
oz. each of the Original flavored Skittles, I used was gathered by members of my class.
Organizing and Displaying Categorical Data: Colors
Results for the entire sample:
Number of
red candies
Number of
orange candies
Number of
yellow candies
Number of
green candies
Number of
purple candies
321
.212
292
.193
306
.209
316
.213
276
.183
Proportion
Results of my 2.17-ounce bag of Skittles:
Number
of red
candies
Number
of orange
candies
8
11
Number
of yellow
candies
25
Number
of green
candies
10
Number
of purple
candies
9
Percentages of Skittle Colors in Class Sample
Pareto Chart of Skittles Color Proportions of Entire Class
In both the Pie, a chart that depicts proportions or percentages of categorical data (colors of
candy per bag) as the slices of a circle, and Pareto, a chart displaying the categorical data in
descending order according to the frequency it occurred, the sample of five different colors from
each bag is totaled and displayed. Both of these graphs depict what I expected to see, some
variance in color distribution per bag, but not by a substantial amount. In comparison, my
individual bag of skittles showed a wider variation in proportion of colors of candies, this was
unexpected.
Organizing and Displaying Quantitative Data: the Number of Candies per Bag
In the table below the data is broken down into categories. The sample size stands for the 25
bags of candy used in the analysis. The mean, 60 is the average amount of candy per bag, the bag
with the lowest amount of candy in the sample contained 53 candies, and the bag with the
highest amount of candy contained 77. You can see that my bag of candy contained an amount
close to the average. The standard deviation, 4.36 denotes how much data values deviate from
the mean, and the Q1, 58, separates the bottom 25% of the sorted value from the top 75% while
Q3, 61, separates the bottom 75% of the sorted values form the top 25%.
Sample
Size
Mean
Candies
per bag
Standard
Deviation
Minimum
Q1
Median
Q2
Q3
25
60.4
4.36
53
58
60
61
Maximum
77
Number
of
Candies
in my bag
63
Histogram Distribution of Class Sample of Skittles Per Bag
Boxplot Distribution of Class Sample of Skittles Per Bag
Histograms show us the shape of distributions of an observation. The shape of the distribution of
the skittle data in the above histogram is skewed to the right because of the outlier, data that lies
an abnormal distance from the other values of skittles per bag in this random sample. The
horizontal scale represents the quantitative data, candies per bag, and the vertical scale represents
the frequency of how many bags out of 25 had which amount of candies.
The boxplot graph, also known as a box-and-whisker diagram, shows a line extending from the
minimum value to the maximum value and a box with lines drawn at the first quartile, median,
and third quartile. It again shows the data skewed to the right—not a normal distribution.
Does the overall data collected by the whole class agree with my own data collected from a
single bag of candies? No! When I sorted my own bag of skittle candies I was definitely
disappointed to find so many lemon yellow candies (25) my least favorite flavor and so few
cherry red (8) and purple grape (9) my most favorite flavors. However when I observed and
analyzed a larger sample size (25 bags) the total amounts sorted by flavor/color was closer in
number. In fact it was interesting to note that cherry red overall was found in the highest amount.
Obviously I grabbed the wrong bag of skittles off the store shelf!
Reflection:
Categorical data consists of names or labels that don’t represent counts or measurements and
quantitative data consists of numbers that do represent counts or measurements. Each type of
data serves a purpose depending on the information you are trying to obtain. For example, if you
want to know the eye color of a group of people categorical data would be what you were after.
The type of graph that would work well for this would be a bar graph, where you can easily
compare the size of the categories or a Pie Chart like the one above. If we wanted to draw
attention to the more important categories a Pareto Chart, works well since it is arranged in
descending order according to the frequencies.
When graphing quantitative data arranged numerically, histograms are best-suited for large
amounts of data, stem and leaf (representing the data by separating each value into two parts)
work well for small to moderate amounts of data, and box plots are good for showing the
differences between distributions.
Graphs that don’t work well for either type of data are those that contain errors, or may be
misleading in some way, like for quantitative data if the vertical axis doesn’t start with zero the
differences between the categories could be exaggerated. Pictographs can also be misleading
when the size of something is not shown in scale to the size of what it’s being compared to.
Confidence Interval Estimates
A confidence interval is a range of values used to estimate the true value of a population
parameter. In other words, if surveying an entire population isn’t a practical option and you
wanted the average weight of all 10 year-old-girls of a given country you would compute the
average weight of a sample of 10-year-old girls in order to estimate the average weight of the
population.
1). 99% Confidence Interval Estimate for the true proportion of yellow skittle candies:
(See attached work below)
Interpretation:
I’m 99% confident the proportion of yellow skittles per bag is between .1764 and .2296.
2). 95% Confidence Interval Estimate of the mean (average) number of candies per bag:
Interpretation:
I’m 95% confident the mean numbers of candies per bag is between 58.6 and 62.2.
3). 98% Confidence Interval Estimate for the standard deviation (a measure of how much data
values deviate away from the mean) of the number of candies per bag:
Interpretation:
I’m 98% confident the standard deviation of the number of candies in a bag is between 3.26 and
6.48.
Hypothesis Tests
A hypothesis in statistics is making an assumption or claim about a something in a population
parameter which may or may not be true. There are two types: a null hypothesis is saying some
value of the population parameter like a proportion or mean is equal to a claimed value, and the
alternative hypothesis says that the parameter has a value that differs from what the null
hypothesis stated. A hypothesis test is a procedure for testing the claim.
1). The hypothesis test to claim that 20% of all skittles candies are red: (see attached work)
Conclusion: Since the p-value, or probability of getting a value of the test statistic that is at least
as extreme as the one representing the sample data, .2262, is greater than 20%, there isn’t
sufficient evidence to reject the claim that 20% of all skittles candies are red, which means it’s
likely, 20% of skittles are red.
2). The hypothesis test to claim that the mean number of candies in a bag of skittles is 55:
Conclusion: The critical value was 2.797 and the test statistic was 6.1926, which is in the critical
region. Using the critical value method (a value separating the critical region where we reject the
null hypothesis from the values not in the critical region that don’t lead to rejection of the null
hypothesis) I rejected the null hypothesis that the mean number of candies in a bag of skittles is
55. I can assume the mean number of candies is close to 55, but I can’t say it is 55.
Reflection:
With sample data and the use of specific formulas the estimate values of population parameters
can be obtained, as well as testing a hypothesis or claim about population parameters.
A confidence interval estimate gives us a better sense of how good a given estimate is. When
different degrees of confidence are used like, 90%, 95% and 99%, the most common three, the
process will result in confidence interval limits that contain the true population proportion, mean,
or standard deviation. As long as the intervals are interpreted correctly the success rate of valid
results in the given procedure increases.
In hypothesis testing after the null hypothesis and alternative hypothesis is identified the test
statistic is calculated given a claim and sample data, the sampling distribution that is relevant is
chosen, the p-value, probability value a test statistic as least as extreme as the one obtained or
critical value, the value corresponding to a given significance level is found and the conclusion
about the claim is stated.
In order for the calculations to be valid, certain requirements must be met. When dealing with
proportions for confidence interval estimates, the sample must be a simple random sample of
independent sample units, have a fixed number of independent trials with two categories of
outcomes, the probabilities remaining constant for each and there are at least 5 successes and 5
failures (binomial distribution). When testing a claim about the population proportion the
requirements are the same so the binomial distribution of sample proportions can be
approximated by a normal distribution using the correct formula.
For estimating the population mean, the sample also needs to be a simple random sample, with
normal distribution or sample values greater than 30, and is the same for testing a claim about a
mean. When estimating the population standard deviation the sample needs to be a simple
random sample and the population must have normally distributed values (even if sample is
large). This requirement is strict when testing a claim about the standard deviation because
departures from normal distributions can result in large errors.
My samples didn’t meet all the above requirements because the sample I used came from 25
bags of skittles purchased independently by 25 students in my stats class. Even though these
skittles were purchased from different stores along the Wasatch Front in the state of Utah they
probably came from the same supplier. This means the sample probably wasn’t a simple random
sample. I also assumed the sample was a normal distribution in which the frequencies start low,
then increase to one or two high frequencies, and decrease to a low frequency—approximately
symmetric but I don’t know for sure. Lastly, my sample size was 25, not greater than 30. These
errors limit the true validity of all my tests.
From my research I can conclude that approximately 20% of skittle candies probably are red and
that the mean average of skittles per bag size of 2.17 oz. is probably around 55 but I don’t know
for sure. If I wanted more accurate conclusions overall I would need to improve the sampling
methods by obtaining skittle samples directly from the manufacturer or from random stores
worldwide. I would need more than 30 for estimating the mean, and would need to verify the
sample was normally distributed in order to obtain a more accurate standard deviation.