Download The purpose of this project is to sufficiently

Math 1040 Skittles Term Project, Part I
1 RECORD INDIVIDUAL INFORMATION ON 2.17 OZ. BAG OF SKITTLES
Color of Skittles
Number of Skittles
Red
13
Orange
5
Yellow
14
Green
12
Purple
14
Total:
58
Math 1040 Skittles Term Project, Part II
2 INTRODUCTION
Each student was required to purchase a 2.17-ounce bag of original Skittles and record
the number of each color included in the bag. The data provided by each student was recorded in
an Excel program, which ultimately provided information on the total number of candies in each
bag, the total number of bags, and the total number of candies. This is the data each student
would use to complete each section of the term project.
The purpose of this project is to sufficiently demonstrate the skills learned in this class.
To do so, every student is required to submit the following work:

Properly organize and analyze the data provided in the Excel program mentioned above

Use confidence intervals and hypothesis tests to draw appropriate conclusions

Determine the proportion of each Skittle color by organizing the categorical data in both
Pie and Pareto Chart form (include tables along with the Pie and Pareto chart which
comprise of the results of my own bag of Skittles and the results for the entire sample)

Write an observational paragraph on the data collected above: include the shape of the
graph, if the graphs reflect what might be expected and if the overall data collected by the
whole class agree with the data provided by my own bag of Skittles

Organize the quantitative data of the mean number of candies per bag. Include the mean,
standard deviation, and 5-number summary

Create a frequency histogram and boxplot for the data mentioned above

Write a reflection paragraph on the difference between categorical and quantitative data:
discuss what types of graphs do and don’t make sense for categorical and quantitative
data, and which types of calculations do and don’t make sense for categorical and
quantitative data

Explain the purpose and meaning of a confidence interval

Construct a 95% confidence interval estimate for the true proportion of purple candies

Construct a 99% confidence interval estimate for the true mean number of candies per
bag

Construct a 98% confidence interval estimate for the standard deviation of the number of
candies per bag

Discuss, interpret and scan copies the results of each interval estimates

Explain the purpose and meaning of a hypothesis test

Use a 0.01 significance level to test the claim that 20% of all Skittles candies are green

Use a 0.05 significance level to test the claim that the mean number of candies in a bag of
Skittles is 56

Discuss, interpret, and scan copies of the results of each hypothesis test

Write a reflection paper which states the conditions for doing interval estimates for
population standard deviations, as well the conditions for doing interval
estimates/hypothesis tests for population proportions and population means. Determine
whether or not my sample met these conditions, the possible errors that could have
occurred by using this data, and how the sampling method could be improved

Write an additional reflective paper, which must be at least one page in length. This paper
must include what I have learned from this project and how the math skills acquired in
this class may be applied for other classes, or how this project supported my views about
real-world math applications
3 ORGANIZING AND DISPLAYING CATEGORICAL DATA BY COLOR
Number of Skittles, condensed version
Individual
Group
Red
13
251
Orange
5
238
Yellow
14
250
Green
12
249
Purple
14
264
Total
58
1252
Number of Skittles, enhanced version
Red
Orange
Yellow
Green
Purple
Total
13
5
14
12
14
58
9
8
15
11
17
60
13
11
10
13
12
59
13
7
14
10
14
58
16
12
12
2
9
51
10
9
13
14
12
58
14
14
10
11
13
62
12
13
12
10
11
58
16
9
7
15
15
62
10
13
13
9
12
57
15
12
7
12
15
61
11
14
11
17
10
63
14
12
13
7
15
61
10
13
8
11
16
58
10
12
17
10
11
60
7
11
21
13
7
59
12
14
13
12
11
62
18
10
6
16
9
59
13
7
9
13
19
61
7
18
12
15
9
61
8
14
13
16
13
64
251
238
250
249
264
1252
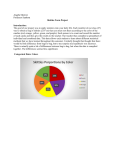
Individual Pie Chart (sample size 58 candies)
Red= .224
Orange= .086
22.414%
24.138%
Yellow= .241
Green= .207
8.621%
Purple= .241
20.690%
24.138%
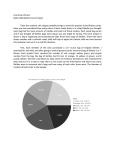
Entire Sample Pie Chart (sample size 1252 candies)
Red= .200
20.048%
21.086%
Orange= .190
Yellow= .200
Green= .199
19.010%
19.888%
Purple= .211
19.968%
Individual Pareto Chart (sample size 58 candies)
16
Number of Skittles
14
12
10
8
6
4
2
0
Red= .224
Green= .207
Yellow= .241
Orange= .086
Purple= .241
Colors of Skittles, decimals portray percentage amount
Entire Sample Pareto Chart (sample size 1252 candies)
270
Number of Skittles
265
260
255
250
245
240
235
230
225
Red= .200
Orange= .190
Yellow= .200
Green= .199
Purple= .211
Color of Skittles, decimals portray percentage amount
Having access to the data for both the individual and group results, the graphs do reflect
what I expected to see. However, when you compare the data from both sets, my data doesn’t
completely agree with the group data-my number of orange Skittles is extremely low compared
to the class average. Be that as it may, having results from only one bag of Skittles doesn’t
reflect the entire amount of candy distributed by that company-a larger sample size would be
needed.
4 ORGANIZING AND DISPLAYING QUANTITATIVE DATA: THE NUMBER OF
CANDIES PER BAG
Calculate the mean, standard deviation and 5number summary by using the total number of
candies in each bag in the class sample.
To calculate the mean, I added the total number of candies in each bag and divided it by the
number of bags. So, in this case, the equation is as followed:
(58+60+59+58+51+58+62+58+62+57+61+63+61+58+60+59+62+59+61+61+64)
21
= 1252
21
= 59.6
The mean number of candies for every bag of candy in the class sample is 59.6.
To calculate the standard deviation, I used my TI-83 Plus calculator. The standard
deviation for the total number of candies in each bag in the class sample is 2.75.
The five-number summary consists of the minimum number, first quartile, median, third
quartile and maximum number of the given series. Each category of the five-number summary is
listed below:
(Numbers listed in ascending order)
51 57 58 58 58 58 58 59 59 59 60 60 61 61 61 61 62 62 62 63 64
Minimum number: 51
First quartile= ¼ (n+1):
¼ (22) = 5.5. 5 ½ numbers from the left is 58. Therefore, the first quartile number is 58.
Median ("middle number" in a sorted list of numbers): 60
Third quartile= ¾ (n+1):
¾ (22) =16.5. 16 ½ numbers from the left is 61.5. Therefore, the third quartile number is 61.5.
Maximum number: 64
Frequncy
Class Sample Frequency Histogram
11
10
9
8
7
6
5
4
3
2
1
0
50-53
54-57
58-60
61-63
Candies per bag (21 bags total)
64-66
I would consider this to be a bell-shaped graph. The even points on both the left and right
side of the graph lead me to believe this is a normal distribution. With the number of bags
written in ascending order, it is easier to see that it has a bell shape, therefore the graphs do
reflect what I expected to see. Overall, with the orange Skittles being the small exception, the
data collected by the class agrees with my own data.
5 REFLECTION
What is the difference between categorical and quantitative data? Categorical data is
information that is organized into groups (or categories, as the name implies), while quantitative
data is comprised of data that can be counted or measured.
Common categories used for categorical data include information on age, race, or sex. To
correlate it with this exercise, the categorical data would be the colors of Skittles included in a
certain number of bags. Only being provided with the number of Skittles would make a very
short list without the category to define what the numbers are there for.
On the other side of the spectrum, quantitative data is strictly numerical. A couple examples
of this would be the lengths of newborn babies born on a certain day, or the heights of trees in a
specific area-or, let’s say, the number of Skittles in x amount of bags. Without quantitative data
for this exercise, I would have a graph simply labeled as “Skittles: red, green, yellow, orange and
purple.” While this would make a colorful graph, it probably would not be very useful.
So what information would not be useful for these data sets? If I needed to compile a
graph of the percentage grades of each student in a particular class, gathering each students’ hair
color would not contribute to this list at all. On the other side of that, if I were wanting to record
the hair color of each student in the same class, obtaining their grade would be just as redundant.
Math 1040 Skittles Term Project, Part III
6 CONFIDENCE INTERVAL ESTIMATES
What is the general purpose and meaning of a confidence interval? Confidence intervals are
a type of estimate of a population parameter. They consist of a range of values that are likely to
contain the population parameter of interest. Confidence intervals give acceptable estimates of
the unknown part of a population parameter.
To determine such estimates, confidence intervals are constructed at a certain confidence
level, which is set by the person conducting the study. The confidence level reflects the true
population parameter percentage. For example, if the confidence level equals 98 percent, then it
can correctly be assumed that the interval estimates would include the true population parameter
in about 98 percent of the studies. The confidence level is typically 95 percent, unless otherwise
stated. Because of this, the user will occasionally overlook stating the confidence level in their
study.
There is a 95 percent confidence level that the interval between .1883 and .2335 contains
the true value of the population proportion p. That means that out of numerous samples with a
sample size of 1252, 95 percent of them would contain the value of the population proportion p.
Based on these calculations, there is 99 percent confidence that the interval between
57.893 and 61.307 contains the true value of mean. That means that out of numerous samples
with a sample size of 1252, 99 percent of them would contain the value of the population
proportion p.
Based on these results, there is a 98 percent confidence that the boundaries of 2.01 and
4.28 contain the true value of the standard deviation.
7 HYPOTHESIS TESTS
Hypothesis testing is used to deduce the result of a hypothesis being performed on sample
data which is derived from a larger population. The way to do this is to either accept or reject
the null hypothesis. The null hypothesis is the common view of a subject, and is portrayed as
(H0). The analyzer tries to reject or nullify null hypothesis, because they believe the alternative
hypothesis is correct.
8 REFLECTION

State the conditions for doing interval estimates and hypothesis tests for population
proportions and discuss whether or not your samples met these conditions.
An interval estimate is defined by two numbers, between which a population parameter lies.
For example, p̂ - E < p < p̂ + E. The sampling method must be simple random sampling, which
is a randomly selected sample from a larger sample or population. The sampling distribution is
normally distributed.
For hypothesis testing, normal distribution is required unless the samples size is greater than 30.
If the sample is (1) obtained using simple random sampling, (2) has no outliers, and (3) is
normally distributed, then the t-distribution must be used to test the hypothesis.
The sample size was from 21 students (therefore, under 30), so normal distribution
needed to be used. The bell-shaped graphs included in part II of the assignment helped visibly
show that the information was normally distributed. There were no major outliers. And while
the group performing the Skittle project was not huge, I felt that there were enough people
present to adequately present the larger population.

State the conditions for doing interval estimates and hypothesis tests for population
means and discuss whether or not your samples met these conditions.
For doing interval estimates, a few things are needed: (1) x̄, which is the sample mean, (2)
the standard deviation, where the standard deviation = s, (3) the degrees of freedom (or “df”),
which is found by subtracting one from n (or the sample size), (4) p̂, which is x-bar divided by
the sample size.
To determine the population mean, x-bar must be present, as well as the mean, standard
deviation and the sample size. All of the above were present in this project, therefore my
samples met these conditions.

State the conditions for doing interval estimates for population standard deviations and
discuss whether or not your samples met these conditions.
With population standard deviations, the x-bar isn’t provided, so chi-square will need to
be used. The standard deviation and sample size must also be present. The Excel data sheet
provided with the class data provided all of the information needed, therefor my samples met
these conditions.

What possible errors could have been made by using this data? How could the sampling
method be improved? State what conclusions you have drawn from your statistical
research.
The data provided appeared to be sound, so I don’t believe any errors could have been made.
However, while I think the sample size was adequate, I think the results could have been more
accurate if the sample size was a little larger.
Math 1040 Skittles Term Project, Part IV
REFLECTIVE WRITING

What have you learned as a result of this project?
The Skittles term project was an extensive project that enabled me to use and learn a variety
of skills. Because of this, there were many things I learned while completing this task. To
properly complete it, I needed to collaborate many of the things I learned while taking this
class.
Organizing and displaying data by color was one of the skills I utilized while completing
this activity. One of the requirements of the project was to create a Pie chart, Pareto chart,
frequency histogram, and boxplot in an Excel document. This created an effective visual guide
to help determine the proportion of each color within the comprehensive sample collected by
the class.
Another requirement of the project involved using some of the formulas used throughout the
semester. These formulas assisted in determining the mean, standard deviation, and 5-number
summary, confidence interval estimates, and hypothesis testing of the data gathered by the class.
This project also utilized my writing skills. In addition to creating visual charts and using the
formulas learned throughout the semester, I had to write reflective paragraphs explaining the
difference between categorical and quantitative data (determined by the visual graphs) and what
conditions are necessary for interval estimates during specific population proportion scenarios
(determined by the formulas I had to use to find confidence interval estimates and hypothesis
testing). Writing these papers was an effective way to understand the assignment from another
perspective.