Download 12.1 - Probability Distributions

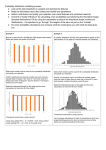
12.1 – Probability
Distributions
Frequency Table

A frequency table is a list of outcomes in a
sample space and the number of times each
outcome occurs
Sample: Make a frequency table of each person’s
hair color in the room
Blondes Black Brunettes
Red Highlights

Let’s Review

What is the difference between experimental and
theoretical probability?

Experimental: Finding the probability based on trials
(or experiments).

Theoretical: The chances of “winning” if there are an
equally likely number of outcomes.
Let’s Try Some

Kelly is competing in the Rock, Paper,
Scissors Championships at the Martinez Cow
Pie Festival (her eighth time competing).
What is the theoretical probability of her
playing a rock, paper, or scissors?
1
3
How can we determine if the
theoretical probability matches
the experimental?
Copy the table
1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2
0 1 2 3 4 5 6 7 8 9 0
P1
P2
Challenge 20 people to a RPS Game
(best of one game)
In the table, you are player one. List the hand played
when one of you wins. Circle the winning play
1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2
0 1 2 3 4 5 6 7 8 9 0
P1
P2
Finally, determine the experimental probability of each winning play.
How close is it to the experimental?
How can you get the experimental to match the theoretical?
Probability Distribution

A probability distribution is a function that
gives the probability of each event in a sample
space. You can use a table or a graph to show
the probability distribution.
Example:

You have two spinners. Each spinner has 4
possible outcomes: 1, 2, 3, or 4. Show the
probability distribution for the SUM of the
numbers. Find the frequency and probability.
Sum
2
3
4
5
6
7
8
Frequency
1
2
3
4
3
2
1
Probability
1/16
1/8
3/16
1/4
3/16
1/8
1/16
Graphing the Distributions
Use a bar chart to graph the probability distribution
3/10
1/4
1/5
3/20
1/10
1/20
0
1
2
3
4
5
6
7