Download The Wave

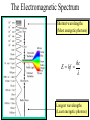
The Wave – Particle Duality
OR
Light Waves
Until about 1900, the classical wave theory of light described
most observed phenomenon.
Light waves:
Characterized by:
 Amplitude (A)
 Frequency (n)
 Wavelength (l)
Energy a A2
And then there was a problem…
However, in the early 20th century, several effects
were observed which could not be understood using
the wave theory of light. So other experiments were
done and found it could behave as both::
1) The Photo-Electric Effect (particle)
2) The Compton Effect (particle)
3) Taylor’s experiment (wave)
4) DeBroglie Wavelength (wave)
Quantized Model of Light
(Photons)
• In 1900 Max Planck proposed that light
energy comes in packets (quanta) spread at
random on a wave front called PHOTONS.
• He even doubted his idea since:
It went against wave theory by saying that
electromagnetic waves don't transmit energy
continuously but in small packets.
It went against Newtonian physics since
objects aren't free to vibrate with any energy.
The energy only has certain discreet values.
Quantized Model of Light
Energy of a light particle (Photon):
E photon  hf 
hc
l
h = 6.6x10-34 [J*sec]
Planck’s constant, after the scientist Max Planck
The Electromagnetic Spectrum
Shortest wavelengths
(Most energetic photons)
E  hf 
hc
l
Longest wavelengths
(Least energetic photons)
Photons
Problems:
1. Find the energy in electron volts (eV) for a
quantum of orange light with frequency 5.00 x
1014 Hz. (Answer: 2.07eV)
2. Find the energy in electron volts for a quantum of
yellow light with a wavelength of 580 nm.
(Answer: 2.14 eV)
Suggested Textbook Problems:
Page 597 #2-6
Photoelectric Effect
“Classical” Method
What if we try this ?
Increase energy by
increasing amplitude
Vary wavelength, fixed amplitude
electrons
emitted ?
No
No
No
No
electrons
emitted ?
No
Yes, with
low KE
Yes, with
high KE
No electrons were emitted until the frequency of the light exceeded
a threshold frequency, f o at which point electrons were emitted!
Photoelectric
Electrons are attracted to the (positively charged) nucleus by the
electrical force
In metals, the outermost electrons are not tightly bound
If given energy electrons can be freed
Classically, we increase the energy
of an EM wave by increasing the
intensity (e.g. brightness)
Energy a A2
But this doesn’t work ??
PhotoElectric Effect
An alternate view is that light is acting like a particle
The light particle (photon) must have enough energy to “free” the
electron
Increasing the Amplitude is just simply increasing the number
of light particles, but its NOT increasing the energy of each one!
However, if the energy of these “light particle” is related to their
frequency, this would explain why higher frequency light can
knock the electrons out of their atoms, but low frequency light
cannot…
Photo-Electric Effect
• See diagram below …the energy of the
light particle (photon) must overcome the binding energy of the
electron to the nucleus (Work)
• Ephoton = Ek + Work.
• Ek = Ephoton – Work. (Einstein’s Photoelectric Equation)
“Light particle”
Metal Surface
“Freed” electron has Ek
Work to free elctron
Photo-Electric Problems
1. EM radiation of frequency 7.0 X 1014 Hz falls on a
metal with work function of 0.5eV.
a) Calculate the maximum kinetic energy of the
emitted photoelectrons and the maximum speed
of the emitted photoelectrons.
(Answer: 3.8 x 10 –19 J)
NOTE: Remind students if questions ask for
speed make sure you convert everything into
Joules.
b) What would be the case if the kinetic energy was
less than 0.5 eV. (Answer: no emission)
Photo-Electric Problems
2. Calculate the Threshold (minimum) frequency for a
metal with a work function or binding energy of 1.5
eV. (Answer: 3.6 x 1014)
3. A photoelectric surface has a work function of 1.50
eV. A red light of wavelength 650 nm is directed at
the surface. Calculate:
a) The maximum Ek of the emitted
photoelectrons in joules (Answer: 6.60 x 10 -20 J)
b) The photoelectrons' maximum speed
(Answer: 3.81 x 10 5 m/s)
c) The cutoff potential needed to stop the
photoelectrons (Answer: 0.412 V)
Photo-Electric Problems
Suggested Text Questions:
Pg. 604 #10-15
The Compton Effect
1924 Compton performed the photoelectric exp with Xrays .
Like the photoelectric effect it showed light behaving as
a particle.
Incident X-ray
l1
M
A
T
T
E
R
Scattered X-ray
l2
e
Electron comes flying out
The Compton Effect
Energy and momentum are conserved
Exray photon
'
E
xray photon
 Ek electron
Notice: There is NO work function since it is
negligible (compared to x-ray energy).
The Compton Effect
Compton derived the expression for
momentum of a photon.
E  mc 2
p
h
l
E photon  mc 2
mc 
E photon
p photon
p photon
c
hf

c
h

l
Bohr’s Complementarity
Principle
If light is passing through a medium treat
it like a wave.
If light is reacting with matter treat it as a
particle.
Wave Nature of Matter
DeBroglie thought:
“If light waves can behave like a particle, might
particles act like waves”?
DeBroglie’s wavelength:
h
h
l 
p mv
Matter Waves (cont)
Ex 1: Compute the wavelength of a 1 [kg]
block moving at 1000 [m/s].
l = h/mv
= 6.6x10-34 J s/(1kg)(1000 m/s)
= 6.6x10-37 [m].
 VERY small. therefore wave behavior of
matter can’t be seen.
Electron Microscope
The electron microscope is a device which uses the
wave behavior of electrons to make images
which are otherwise too small using visible light!
This image was taken with a Scanning
Electron Microscope (SEM).
These devices can resolve features down
to about 1 [nm]. This is about 100 times
better than can be done with visible light
microscopes!
IMPORTANT POINT HERE:
High energy particles can be used to reveal the structure of matter !
High Energy Particles
High energy particles can provide a way to reveal the
structure of matter beyond what can be seen using an
optical microscope.
The higher the momentum of the particle, the smaller the
deBroglie wavelength.
As wavelength decreases, finer and finer details about the
structure of matter are revealed !
This is done at facilities often referred to as “atomsmashers” or “accelerators”