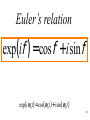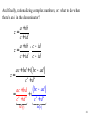* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slides A - Department of Physics | Oregon State
Velocity-addition formula wikipedia , lookup
Fictitious force wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Brownian motion wikipedia , lookup
Atomic theory wikipedia , lookup
Classical mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Specific impulse wikipedia , lookup
Center of mass wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Jerk (physics) wikipedia , lookup
Proper acceleration wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Classical central-force problem wikipedia , lookup
424: Oscillations & Waves
1
PH424: Homework 30%;
Laboratory reports 35%;
Final 35%.
Mon
Tue
13
14
Simple Harmonic Motion - Free motion of an
- 4 representations
oscillator
-Free damped
oscillations
Feb & March 2017 ~
Wed
15
-PS1a due
Fri
16
17
Upload data
Lab & Discussion: -PS1b due
the LCR circuit
Forced motion of a damped
oscillator
LCR circuit resonance
23
24
-PS2b due
(Math Methods)
(Math Methods)
20
Forced motion of a
damped oscillator
-data workshop
o phase shifts
o resonance
27
(Math Methods)
Formal LCR Lab
Report Due
(in class)
21
6
-Multiple Driving
Frequencies
7
8
9
Fourier coefficients &
Wave Mechanics
transform
-PS4a due
Fast Fourier Methods Fast Fourier Transform
& Impulse Demo Lab
10
14
17
13
22
-PS2a due
Thu
Forced motion &
resonances
(Math Methods)
28
(Math Methods)
1
-PS3a due
-The Fourier Series &
Transform
2
Lab & Discussion:
Coax Cable Lab
Intro to Wave Reflection Workshop
& Transmission
Pre-Lab
15
16
3
-PS3b due
Lab Data Workshop
Upload data
-PS4b due
2
Introducction to Formal
Technical Writing
• Two “formal” lab reports (35%) are required.
Good technical writing is very similar to writing an
essay with sub-headings.
We want to hear a convincing scientific
story, not a shopping list of everything you did.
• Check out course web-site
• We will have data & write-up workshops
3
Are oscillations ubiquitous
or are they merely a paradigm?
Superposition of 4
brain neuron activity
for our purposes ….
Oscillations modulations in time
Waves modulations in space
Superposition of 5
brain neuron activity
REPRESENTING SIMPLE HARMONIC
MOTION
simple
not simple
6
http://hyperphysics.phy-astr.gsu.edu/hbase/imgmec/shm.gif
Simple Harmonic Motion
y(t)
Watch as time evolves
7
x(t) = A cos (w 0t + f )
phase
angle
amplitude
position
1
T=
=
w0 f
angular freq
(cyclic) freq
x0
-0.25
-A
2p
1
A
f
t=w0
period
0.25
0.75
1.25
1.75
-1
time
determined by initial conditions
determined by physical system
8
1
0.5
Position (cm)
x(t) = A cos (w 0t + f )
0
-0.5
x
-1
0
t
1
2
0
t
1
2
0
t
1
2
6
4
2
Velocity (cm/s)
0
x(t) = Aw 0 cos (w 0t + f + p2 )v
-2
-4
-6
40
20
Acceleration (cm/s2)
0
x(t) = Aw cos (w 0t + f + p )a
2
0
-20
-40
time (s)
9
These representations of the position of a simple harmonic
oscillator as a function of time are all equivalent - there are 2
arbitrary constants in each. Note that A, f, Bp and Bq are
REAL; C and D are COMPLEX.
x(t) is real-valued variable in all cases.
A:
x(t) = Acos(w0t + f )
B:
x(t) = B p cos w 0 t + Bq sin w 0 t
C:
x(t) = C exp(iw 0 t ) + C * exp(-iw 0 t )
D:
x(t) = Re[ D exp(iw 0 t )]
Engrave these on your soul - and know how to derive the
relationships among A & f; Bp & Bq; C; and D .
10
Example: initial conditions
k
m
x(t) = Acos(w0t + f )
k
x(t) = B p cos w 0 t + Bq sin w 0 t
m
x
m = 0.01 kg; k = 36 Nm-1. At t = 0, m is displaced 50mm to
the right and is moving to the right at 1.7 ms-1.
Express the motion in
form A
form B
11
x(t) = Acos(w0t + f )
(
)
x(t) = 57.5 cos éë 60s ùû t - 0.516 mm
-1
x(t) = B p cos w 0 t + Bq sin w 0 t
(
)
(
x(t) = 50mm cos éë 60s -1 ùû t + 28.3mmsin éë 60s -1 ùû t
Bp = Acos f
Bq = -Asin f
A = Bp + Bq
2
tan f = -
)
2
Bq
Bp
12
Using complex numbers: initial conditions. Same
example as before, but now use the "C" and "D" forms
k
k
m
x(t) = C exp(iw 0 t ) + C * exp(-iw 0 t )
x(t) = Re[ D exp(iw 0 t )]
m
x
m = 0.01 kg; k = 36 Nm-1. At t = 0, m is displaced 50mm to
the right and is moving to the right at 1.7 ms-1.
Express the motion in
form C
form D
13
x(t) = C exp(iw 0 t ) + C * exp(-iw 0 t )
x(t ) (25 14.16i)e
i 60s 1t
(25 14.16i)e
i 60s 1t
mm
x(t) = Re[ D exp(iw 0 t )]
x(t ) Re 50 28.3i e
i 60s 1t
mm
Acos f = Bp = 2Re[C ] = Re[ D]
Asin f = -Bq = 2Im[C] = Im[ D]
D = 2C = A
Im[ D] Im[C ]
tan f =
=
Re[ D] Re[C14]
Differential Equation
Representation
our equation
is a second-order ODE
our basis can be
{cos(wt), sin(wt)}
But all linear combinations are solutions,
i.e., Acos(wt) + Bsin(wt)
Consider all the equivalent
solutions
what about Asin(wt+f) ?
Asin(wt+f)
=A{sin(wt) cos(f) + cos(wt) sin(f)}
=Acos(f) • sin(wt) + Asin(f)•cos(wt)
=A' sin(wt) + A' tan(f)•cos(wt)
= A' sin(wt) + B' cos(wt)
so Asin(wt+f) gives all linear
combinations of basis solutions
… spans the space
Clicker Questions
17
A particle executes simple harmonic motion.
When the velocity of the particle is a maximum which one of
the following gives the correct values of potential energy and
acceleration of the particle.
(a)potential energy is maximum and acceleration is maximum.
(b)potential energy is maximum and acceleration is zero.
(c)potential energy is minimum and acceleration is maximum.
(d)potential energy is minimum and acceleration is zero.
18
A particle executes simple harmonic motion.
When the velocity of the particle is a maximum which one of
the following gives the correct values of potential energy and
acceleration of the particle.
(a)potential energy is maximum and acceleration is maximum.
(b)potential energy is maximum and acceleration is zero.
(c)potential energy is minimum and acceleration is maximum.
(d)potential energy is minimum and acceleration is zero.
Answer (d). When velocity is maximum displacement is zero so
potential energy and acceleration are both zero.
19
A mass vibrates on the end of the spring. The mass is replaced
with another mass and the frequency of oscillation doubles.
The mass was changed by a factor of
(a) 1/4
(b) ½
(c) 2
(d) 4
20
A mass vibrates on the end of the spring. The mass is replaced
with another mass and the frequency of oscillation doubles.
The mass was changed by a factor of
(a) 1/4 (b) 1/2 (c) 2 (d) 4
Answer (a). Since the frequency has increased the mass must
have decreased. Frequency is inversely proportional to the
square root of mass, so to double frequency the mass must
change by a factor of 1/4.
21
A mass vibrates on the end of the spring. The mass is replaced
with another mass and the frequency of oscillation doubles. The
maximum acceleration of the mass:
(a)
(b)
(c)
(d)
remains the same.
is halved.
is doubled.
is quadrupled.
22
A mass vibrates on the end of the spring. The mass is replaced
with another mass and the frequency of oscillation doubles. The
maximum acceleration of the mass:
(a)
(b)
(c)
(d)
remains the same.
is halved.
is doubled.
is quadrupled.
Answer (d). Acceleration is proportional to frequency squared. If
frequency is doubled than acceleration is quadrupled.
23
A particle oscillates on the end of a spring and its position as a
function of time is shown below.
At the moment when the mass is at the point P it has
(a) positive velocity and positive acceleration
(b) positive velocity and negative acceleration
(c) negative velocity and negative acceleration
(d) negative velocity and positive acceleration
24
A particle oscillates on the end of a spring and its position as a
function of time is shown below.
At the moment when the mass is at the point P it has
(a) positive velocity and positive acceleration
(b) positive velocity and negative acceleration
(c) negative velocity and negative acceleration
(d) negative velocity and positive acceleration
Answer (b). The slope is positive so velocity is positive. Since the
slope is getting smaller with time the acceleration is negative. 25
Optional Review of Complex Numbers
26
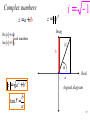
i = -1
Complex numbers
z = a + ib
Re ( z ) = a üï
ý real numbers
Im ( z ) = b ïþ
z = ze
if
Imag
|z|
b
f
a
z = a +b
2
2
Real
Argand diagram
b
tan f =
a
27
Euler’s relation
exp(if) = cos f + isin f
exp(iw 0 t ) = cos(w 0 t ) + i sin(w 0 t )
28
Consistency argument
z = z e if
z = a + ib
If these represent the same thing, then the assumed Euler
relationship says:
a + ib = z cos f + i z sin f
Equate real parts:
Equate imaginary parts:
z = a +b
2
2
a = z cos f
b = z sin f
b
tan f =
a
29
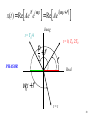
x(t) = Re[ Ae e
if iw 0 t
] = Re[ Ae
i (w 0 t+f )
]
Imag
t = T0/4
p
+f
2
PHASOR
t = 0, T0, 2T0
f
Real
w0t + f
t=t
30
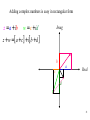
Adding complex numbers is easy in rectangular form
z = a + ib
w = c + id
Imag
z + w = [ a + c] + i [b + d ]
b
a
c
Real
d
31
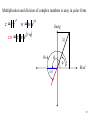
Multiplication and division of complex numbers is easy in polar form
z = ze
if
iq
w= we
Imag
i [f + q ]
zw = z w e
|z|
qf
q
|w|
f
Real
32
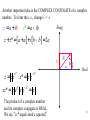
Another important idea is the COMPLEX CONJUGATE of a complex
number. To form the c.c., change i -> -i
z = a + ib
z* = a - ib
Imag
z + z* = [ a + a ] + i [ b - b ] = 2a
b
z = ze
if
z* = z e
if
zz* = z e z e
-if
-if
= z
|z|
a
f
Real
2
The product of a complex number
and its complex conjugate is REAL.
We say “zz* equals mod z squared”
33
And finally, rationalizing complex numbers, or: what to do when
there's an i in the denominator?
a + ib
z=
c + id
a + ib c - id
z=
´
c + id c - id
z=
ac + bd + i ( bc - ad )
c +d
ac + bd ( bc - ad )
= 2
+i 2
2
c +d
c + d2
2
Re ( z )
2
Im ( z )
34