* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Area and Volume - mcs6
Survey
Document related concepts
Transcript
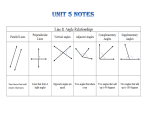
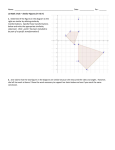
Area—number of square units enclosed Dimensions must all be the same unit Altitude/Height—line perpendicular to the base with triangles, parallelograms, or trapezoids Square/Rectangle Perimeter (distance around) P = 4 x S (square) P=2L+2W Area A = L x W (rectangle) A = S x S (square) Circles Area A = ∏ r ² or ∏ x r x r Circumference C=∏xd (1/2 diameter) Radius Diameter Parallelogram A=bxh Triangle A=½bxh Trapezoid A = ½ h(b1 + b2) *or you can treat the trapezoid like a composite figure by dividing it into simpler figure and finding the area then adding the totals Circles Area -- A = ∏r² Circumference -- C = ∏d or 2r∏ 3-D figures are also called space figures or solids Vertex-where lines meet at a point Base-flat surface on the top and bottom of the figure Base edge-lines along the base Lateral face-flat surface on sides of the figure Lateral edge-lines along the sides of the figure Prism-2 parallel bases are congruent polygons and lateral faces are rectangles sides are always rectangles base (can be any shape; same on both ends) Pyramid-1 polygon base the lateral faces are triangles vertex sides are always triangles base (can be any shape) Cylinder-2 parallel bases that are congruent circles base (always a circle) sides are rounded Cone-1 circular base and 1 vertex vertex base (always a circle) Sphere-all points equal distance from center Net—pattern you can form into a space figure Named for the bases You must know what shape the bases and faces form to be able to figure out a net Cylinder Triangular Prism Cube Rectangular Pyramid Square Root– the inverse of squaring a number Symbol √ The square of an integer/number is a perfect square On calculator: 2nd button then x² button then # then enter Irrational Number—decimal form of a number that neither terminates or repeats If an integer isn’t a perfect square, its square root is irrational The first 13 perfect squares are easy to memorize: 0² = 0 6² = 36 1² = 1 7²= 49 2² = 4 8² = 64 3² = 9 9² = 81 4² = 16 10²= 100 5² = 25 11² = 121 6² = 36 12²= 144 * a square is a number times itself Practice : (simplify & state whether it is rational or irrational) 1.) √64 2.) √100 3.) - √16 4.) - √121 5.) √27 6.) - √72 7.) - √50 8.) √2 Volume—number of cubic units needed to fill in a 3-D figure Cubic unit—space occupied by a cube This is why the units are cubed Rectangular Prism or Cube V=Lxwxh Cylinder V = ∏r2 x h Volume of Triangular V = (1/2 b x h) x h Prism Or V = b x h x h Volume of a Cone or Pyramid 2 Pyramid V = 1/3 ( L x w) x h Or V = l x w x h 3 Cone V = 1/3 (∏ r2) x h Or V = ∏r² x h 3 Surface Area (S.A.)—sum of the area of the bases and the lateral sides of a space figure Draw the figure Fill in all of the numbers for the edges Find area of each face and add everything together Sometimes it helps to draw a net figure then fill in the numbers Find each of the following areas: Lxw Lxh wxh Then add up all areas and multiply answer by 2 6 5 7 S.A. = l x w = lxh= wxh= sum = ? x 2 answer = ? *find area of circle then find area of rectangle *formula for area of rectangle is (∏d x h) Ex: h= 11.5 cm add Area of the circle: A = ∏ r2 A= A=?X2 Area of the rectangle : A = ∏ x d x h A= A=? R = 3.5 cm Total Area = ? * EX: Area of Triangle: A = ½ b x h A = ½ (6 x 4) A=?X2 5 cm 6 cm 6 cm 5 cm 12cm 4 cm * There Area of Rectangle: A = l x w A = 12 x 5 A=?X3 are 3 rectangle so multiply that area by 3 * There are 2 triangles so multiply that area by 2 Total Area = ? Ex: Area of Rectangle: A = l x w A = 12 x 12 A=? 12 m 16 m 12 m Area of the Triangle: A = ½ b x h A = ½ (12 x 16) A=? There are 4 triangles so multiply the area of the triangle by 4. Then add the area of the rectangle to the areas of the triangles. Total Area = ? Ex: Area of the Triangle: A = ½ b x h A = ½ (8 x 10) 10 m 14 cm A=? Area of the Circle: A = ∏ r2 A = 3.14 x 72 A=? Add the areas of the circle and the triangle. Total Area: ? Ex: S.A. = 4∏ r2 d = 5 in S.A. = 4 x 3.14 x 2.52 S.A. = ?