Download Kirchoff Loop Laws …

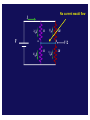
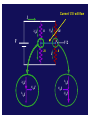
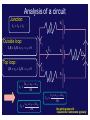
Kirchoff Loop Laws …
I3
I1
Rule 1: “What goes in, must go out “
Rule 2: “What goes up, must come down”
Phys 122 Lecture 14
G. Rybka
I2
Business…
• Exam next Thursday !
• Material is everything through TODAY. – No RC circuits that we will cover Monday
• Practice exam and Eqn. posted on home page after lecture
• Try the SmartPhysics HOMEWORK this week on today’s lessons. Very good practice for multi-­loop problems and a very pedagogical example Can we solve this from simple series and parallel combinations?
Answer: no
Kirchoff Voltage Law: KVL
"When any closed circuit loop is traversed, the algebraic sum of the changes in potential must equal zero."
∑V
n
KVL:
=0
loop
• This is just a restatement of what you already know: that the
potential difference is independent of path!
We will follow the ECE conventions: (engineering)
voltage drops enter with a + sign and
voltage gains enter with a -­ sign in this equation.
Let’s go clockwise around circuit:
ε1
− ε1
I
R1
+ IR1
R2
+ IR2
ε2
+ ε2 = 0
This resistor labyrinth stuff is crazy!
CheckPoint
GAIN
DROP
A
B
C
D
E
With the current
Against the current
VOLTAGE DROP
VOLTAGE GAIN
Examine this loop
R1
b
R4
ε1
f
a
I
I
d
c
R2
ε2
e
R3
Let’s go around the loop counterclockwise from a to f
KVL:
∑ Vn = 0 Þ
IR1 + IR 2 + ε 2 + IR 3 + IR 4 − ε1 = 0
loop
Þ
ε1 − ε 2
I=
R1 + R 2 + R 3 + R 4
Clicker
• Consider the circuit shown. – The switch is initially open and the current flowing through the bottom resistor is I0.
– After the switch is closed, the current flowing through the bottom resistor is I1. 12 V
– What is the relation between I0 and I1?
(a) I1 < I0
(b) I1 = I0
• Write a loop law for original loop:
-12V -12V + I0R + I0R = 0
I0 = 12V/R
• Write a loop law for the new loop:
-12V + I1R = 0
I1 = 12V/R
R
a I
R
b
(c) I1 > I0
12 V
12 V
…or, alternative reasoning
• Consider the circuit shown. – The switch is initially open and the current flowing through the bottom resistor is I0.
– After the switch is closed, the current 12 V
flowing through the bottom resistor is I1.
– What is the relation between I0 and I1?
(a) I1 < I0
(b) I1 = I0
R
a I
R
12 V
12 V
b
(c) I1 > I0
• The key here is to determine the potential (Va-­Vb) before the switch is closed.
• From symmetry, (Va-­Vb) = +12V. • Therefore, when the switch is closed, NO additional current will flow!
• Therefore, the current before the switch is closed is equal to the current after the switch is closed.
Kirchoff's Current Law: KCL
Conservation of Charge (at a junction)
"At any junction point in a circuit where the current can divide (also called a node), the sum of the currents into the node must equal the sum of the currents out of the node."
I in = ∑ I out
I3
I1
I2
CheckPoint
I2
I1
I
I3
I4
Which of the following statements best describes the current flowing i n the blue wire connecting points a and b? Wire connects a to b;; DV through R and 2R to a/b is V/2. (symmetry from below);; Therefore: I1R = I2 2R = V/2;; I1 = V/2R
(twice as much current goes down the left)
From a/b to bottom of circuit, ΔV/2 as well;; I3 2R = I4R = V/2;; I3 = V/4R
(twice as much current down right side)
Junction Rule at a: I1 = Iab + I3 à V/(2R) = Iab + V/(4R) à Iab is positive
Prelecture
CheckPoint
What is the same?
Current flowing in and out of the battery. Equivalent resistance is the same.
2R
3
2R
3
What is different?
Current flowing from a to b.
No current would flow
I
2/
3I
V
R
1/
3I
a
2/
3I
2R
b
R
1/
3I
V/2
2R
Current 1/3 I will flow
I
2/
3I
V
R
1/
3I
a
b
2R
2/ I
3
12/ I
3
2R
I
V/2
R
1/
1/
03I
1/
3I
2/
3I
3I
Have a look at this if you missed it. Some reasoning below …
CheckPoint 7
IA
c
Current will flow from left to right in both cases.
In both cases, Vac = V/2
I2R = 2I4R
IA = IR − I2R
= IR − 2I4R
IB = IR − I4R
IB
c
Analysis of a circuit
Junction:
ε1
I1 = I 2 + I 3
R
Outside loop:
I1R + I 3R + ε 3 − ε1 = 0
I1
I2
ε2
R
Top loop:
I1R + ε 2 + I 2 R − ε1 = 0
I1 =
2 ε1 − ε 2 − ε 3
3R
ε + ε 3 − 2ε 2
I2 = 1
3R
I3
R
ε3
ε + ε 2 − 2ε 3
I3 = 1
3R
No getting around it
3 equations/3 unknowns typically
Clicker
50Ω
a
Consider the circuit shown: – What is the relation between Va -­Vd
and Va -­Vc ?
(a) (Va -Vd) < (Va -Vc)
(b) (Va -Vd) = (Va -Vc)
(c) (Va -Vd) > (Va -Vc)
b
I2
I1
12 V
20Ω
80Ω
d
c
• Remember: potential is independent of path
Going from a to d or c is like going to the same place, electrically
à
(Va -Vd) = (Va -Vc)
Clicker
50Ω
• Consider the circuit shown: – What is the relation between I1 and I2?
12 V
a
b
20Ω
80Ω
d
(a) I1 < I2
• Note that: Vb -Vd
• Therefore, (b) I1 = I2
(c) I1 > I2
= Vb -Vc
I1 (20Ω) = I 2 (80Ω)
I2
I1
I1 = 4I 2
c