* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Kirchoff Loop Laws …
Voltage optimisation wikipedia , lookup
History of electric power transmission wikipedia , lookup
Stepper motor wikipedia , lookup
Ground (electricity) wikipedia , lookup
Mercury-arc valve wikipedia , lookup
Signal-flow graph wikipedia , lookup
Electrical substation wikipedia , lookup
Mains electricity wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Electrical ballast wikipedia , lookup
Stray voltage wikipedia , lookup
Opto-isolator wikipedia , lookup
Circuit breaker wikipedia , lookup
Earthing system wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Current source wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Alternating current wikipedia , lookup
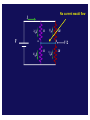
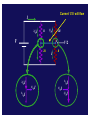
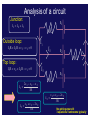
Kirchoff Loop Laws … I3 I1 Rule 1: “What goes in, must go out “ Rule 2: “What goes up, must come down” Phys 122 Lecture 14 G. Rybka I2 Business… • Exam next Thursday ! • Material is everything through TODAY. – No RC circuits that we will cover Monday • Practice exam and Eqn. posted on home page after lecture • Try the SmartPhysics HOMEWORK this week on today’s lessons. Very good practice for multi-loop problems and a very pedagogical example Can we solve this from simple series and parallel combinations? Answer: no Kirchoff Voltage Law: KVL "When any closed circuit loop is traversed, the algebraic sum of the changes in potential must equal zero." ∑V n KVL: =0 loop • This is just a restatement of what you already know: that the potential difference is independent of path! We will follow the ECE conventions: (engineering) voltage drops enter with a + sign and voltage gains enter with a - sign in this equation. Let’s go clockwise around circuit: ε1 − ε1 I R1 + IR1 R2 + IR2 ε2 + ε2 = 0 This resistor labyrinth stuff is crazy! CheckPoint GAIN DROP A B C D E With the current Against the current VOLTAGE DROP VOLTAGE GAIN Examine this loop R1 b R4 ε1 f a I I d c R2 ε2 e R3 Let’s go around the loop counterclockwise from a to f KVL: ∑ Vn = 0 Þ IR1 + IR 2 + ε 2 + IR 3 + IR 4 − ε1 = 0 loop Þ ε1 − ε 2 I= R1 + R 2 + R 3 + R 4 Clicker • Consider the circuit shown. – The switch is initially open and the current flowing through the bottom resistor is I0. – After the switch is closed, the current flowing through the bottom resistor is I1. 12 V – What is the relation between I0 and I1? (a) I1 < I0 (b) I1 = I0 • Write a loop law for original loop: -12V -12V + I0R + I0R = 0 I0 = 12V/R • Write a loop law for the new loop: -12V + I1R = 0 I1 = 12V/R R a I R b (c) I1 > I0 12 V 12 V …or, alternative reasoning • Consider the circuit shown. – The switch is initially open and the current flowing through the bottom resistor is I0. – After the switch is closed, the current 12 V flowing through the bottom resistor is I1. – What is the relation between I0 and I1? (a) I1 < I0 (b) I1 = I0 R a I R 12 V 12 V b (c) I1 > I0 • The key here is to determine the potential (Va-Vb) before the switch is closed. • From symmetry, (Va-Vb) = +12V. • Therefore, when the switch is closed, NO additional current will flow! • Therefore, the current before the switch is closed is equal to the current after the switch is closed. Kirchoff's Current Law: KCL Conservation of Charge (at a junction) "At any junction point in a circuit where the current can divide (also called a node), the sum of the currents into the node must equal the sum of the currents out of the node." I in = ∑ I out I3 I1 I2 CheckPoint I2 I1 I I3 I4 Which of the following statements best describes the current flowing i n the blue wire connecting points a and b? Wire connects a to b;; DV through R and 2R to a/b is V/2. (symmetry from below);; Therefore: I1R = I2 2R = V/2;; I1 = V/2R (twice as much current goes down the left) From a/b to bottom of circuit, ΔV/2 as well;; I3 2R = I4R = V/2;; I3 = V/4R (twice as much current down right side) Junction Rule at a: I1 = Iab + I3 à V/(2R) = Iab + V/(4R) à Iab is positive Prelecture CheckPoint What is the same? Current flowing in and out of the battery. Equivalent resistance is the same. 2R 3 2R 3 What is different? Current flowing from a to b. No current would flow I 2/ 3I V R 1/ 3I a 2/ 3I 2R b R 1/ 3I V/2 2R Current 1/3 I will flow I 2/ 3I V R 1/ 3I a b 2R 2/ I 3 12/ I 3 2R I V/2 R 1/ 1/ 03I 1/ 3I 2/ 3I 3I Have a look at this if you missed it. Some reasoning below … CheckPoint 7 IA c Current will flow from left to right in both cases. In both cases, Vac = V/2 I2R = 2I4R IA = IR − I2R = IR − 2I4R IB = IR − I4R IB c Analysis of a circuit Junction: ε1 I1 = I 2 + I 3 R Outside loop: I1R + I 3R + ε 3 − ε1 = 0 I1 I2 ε2 R Top loop: I1R + ε 2 + I 2 R − ε1 = 0 I1 = 2 ε1 − ε 2 − ε 3 3R ε + ε 3 − 2ε 2 I2 = 1 3R I3 R ε3 ε + ε 2 − 2ε 3 I3 = 1 3R No getting around it 3 equations/3 unknowns typically Clicker 50Ω a Consider the circuit shown: – What is the relation between Va -Vd and Va -Vc ? (a) (Va -Vd) < (Va -Vc) (b) (Va -Vd) = (Va -Vc) (c) (Va -Vd) > (Va -Vc) b I2 I1 12 V 20Ω 80Ω d c • Remember: potential is independent of path Going from a to d or c is like going to the same place, electrically à (Va -Vd) = (Va -Vc) Clicker 50Ω • Consider the circuit shown: – What is the relation between I1 and I2? 12 V a b 20Ω 80Ω d (a) I1 < I2 • Note that: Vb -Vd • Therefore, (b) I1 = I2 (c) I1 > I2 = Vb -Vc I1 (20Ω) = I 2 (80Ω) I2 I1 I1 = 4I 2 c