Download Thales` Triangle Theorem

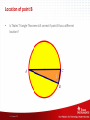
Module C
Geometry with
TI-Nspire™ Technology
Module C
Geometry with
TI-Nspire™ Technology
Lesson 2: Thales’ theorems
In the previous lesson you learned about…
•
•
•
•
•
•
•
The basic terms of geometry.
Angles and angle terms.
Different polygons, rectangles and triangles.
The area, the perimeter and the circumference of the circle.
Coordinates and transformations.
A few important theorems.
The features of TI-NspireTM Technology to teach geometry.
3 | Lesson C.2
TI-NspireTM Technology
In this lesson you will:
•
•
•
Check Thales’ intercept and
Thales’ triangle theorem.
Use the TI-NspireTM Geometry
application to make geometrical
constructions.
Explore the Geometry tools.
Thales of Miletus
4 | Lesson C.2
Thales’ Intercept Theorem
If A is the intersection of two lines AB and AC and
if BC and DE are parallel,
the ratio of BD to DA and
the ratio of CE to EA are equal:
BD CE

DA EA
5 | Lesson C.2
Location of point A
•
Is Thales’ Intercept Theorem still correct if point A has a different
location?
6 | Lesson C.2
Investigation
Steps
•
•
•
•
•
•
•
•
•
Three points A, B, C
Red lines AB and AC
Black line BC
Point D on line AB
Line parallel to BC
Intersection point E
Type formula
Measure lengths of segments
Calculate both sides of the equation
7 | Lesson C.2
BD CE

DA EA
Thales’ Triangle Theorem
If A, B and C are points on a circle
where AC is a diameter of the circle,
then the angle ABC is a right angle.
8 | Lesson C.2
Location of point B
•
Is Thales’ Triangle Theorem still correct if point B has a different
location?
9 | Lesson C.2
Investigation
Steps
•
•
•
•
•
•
Line segment
Midpoint of the line segment
Red circle
Triangle with points on circle
Measure angle
Grab and move point on circle
10 | Lesson C.2
In this lesson you learned …
•
•
•
•
•
•
•
To check Thales’ Intercept theorem and Thales’ Triangle Theorem.
How to use the Geometry application to check a theorem.
How to construct lines, circles, triangles, midpoints, …
How to change the line or fill color.
How to measure lengths, angles, …
How to calculate formulas in the Geometry application.
That the constructions can be used in a dynamic way.
11 | Lesson C.2
Congratulations!
You have just finished lesson C.2!
12 | Lesson C.2