* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Symmetry_of_Properties - IITK - Indian Institute of Technology
Quantum chromodynamics wikipedia , lookup
Thermal expansion wikipedia , lookup
High-temperature superconductivity wikipedia , lookup
Photon polarization wikipedia , lookup
Field (physics) wikipedia , lookup
Noether's theorem wikipedia , lookup
Condensed matter physics wikipedia , lookup
Nordström's theory of gravitation wikipedia , lookup
Density of states wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Metric tensor wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
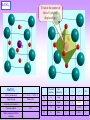
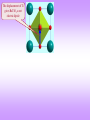
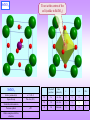
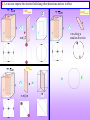
Symmetry of Properties Various properties: Mechanical, Electrical, Magnetic, Thermal, etc. Tensorial nature of properties. Symmetry imposed restraints. Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: [email protected], URL: home.iitk.ac.in/~anandh http://home.iitk.ac.in/~anandh/E-book.htm Advanced Reading Physical Properties of Crystals: Their Representation by Tensors and Matrices J.F. Nye Clarendon Press, Oxford, 1985. Properties of Materials: Anisotropy, Symmetry, Structure Robert E Newnham Oxford University Press, Oxford, 2005. Overview of Properties For now we concern ourselves with properties of crystals For every stimulus there is a natural response. E.g.: when electric field is applied to a dielectric material it can lead to electric polarization, when stresses develop inside a material, it can lead to strains, application of magnetic field can lead to magnetization. In addition there can be cross-coupling terms, i.e. one kind of stimulus can lead to properties, which are not naturally associated with it. E.g.: application of pressure can lead to electric polarization (piezoelectricity), presence of temperature difference can cause electrical potential difference (pyroelectricity), the electrical resistance is altered in the presence of a magnetic field (magnetoresistance). A stimulus can be connected to a response via a material property. E.g.: M = H, = E, P = pi T. The material property has to be measured via experiments (or computed from more fundamental properties). In reality the stimulus and response are tensors (of various orders) and hence the material property is also a tensor of some rank (i.e. many values may be required to describe the property). The equations (as above) in tensorial form become: Mi = ijHj, ij = Eijklkl, Pi = pi T. Classification of material properties Polar tensors (rank 0-4) Axial tensors (rank 0-4) Material Properties Transport properties Relate flow to a gradient Properties with hysterisis Involve domain wall motion Examples of 1st to 4th ranked tensor properties The number of subscripts denotes the order of the tensor Phenomena Pyroelectricity Thermal Expansion Piezoelectricity Elasticity Cause Effect Pi T (Temperature (Electric polarization) difference) T ij (Strain) Pi ij (Electric polarization) (Stress) kl ij (strain) (Stress) Coefficient pi (1st rank tensor) Equation Pi = pi T αij (2nd rank tensor) dijk rd (3 rank tensor) ij = αijT Eijkl (4th rank tensor) Pi = dijkjk ij = Eijklkl Scalar, Vector and Tensor Quantities To describe a property at a point inside the material we may require to specify just a number (magnitude of that property like temperature or density), a magnitude and direction (i.e. 3 numbers in 3D like for electric field or pyroelectric coefficient) or even more numbers. The number of values required is given by 3n in 3D (2n in 2D); where ‘n’ is called the rank of the tensor. To understand why tensors are required let us consider a force ‘F’ (with a F) applied along the x-axis and ask the question*: “what will happen to the body?”. Clearly the information available is insufficient to answer unequivocally. If the forces are applied as in Fig.1b the body will elongate, while if applied as in Fig.1c the body will shear. Hence, we need to specify the plane on which the force is acting. In case in Fig.1b the +F force is acting on the +x-plane along the +x direction this is written as Fxx. In Fig.1c the force +F is acting along the +y-plane along the +x direction written as Fyx. This implies (in this example of mechanical deformation) two directions are required to specify the force (and hence determine its effect): (i) the direction of the plane normal and (ii) the direction of the force. A combination of these forces Fxx & Fxy could also be acting on the body. Fig.1a F F F Fig.1b F Fxx Note. For tension/compression: +F on +x face is positive and similarly, F force on x plane is also positive. For shear: shear causing clockwise rotation is positive. * For now we will assume that other forces are present to give us force and moment balance (i.e. equilibrium condition). F Fig.1c F Fyx Tensors of various ranks Tensors can be used to describe: (i) fields or (ii) properties. These tensors can belong to various ranks: zeroth rank, first rank, second rank, etc. E.g. Temperature field is a scalar field where each point in space is described by one number the ‘T’ at that point (T(x,y,z)). Scalar fields are tensor fields of rank-0. On the other hand some fields require more numbers to be specified at each point in space. Electric field (polar vector) and Magnetic field (axial vector) require three numbers (in 3D) to be specified at each point. These 3 numbers are the components along the coordinate axes and give the direction and magnitude of the vector. Such a field is a vector field. Vectors are tensors of rank-1. Some other fields require more numbers to be specified. E.g. to describe the state of stress at a point, we need 9 numbers (in 3D) in general (stress being a symmetric tensor we actually need only 6 numbers). Stress is a tensor of rank-2. The number of values required to be specified can be thought of as the number of directions involved. This is specified by adding subscripts to the parameter. A scalar involves zero directions and does not have a subscript (e.g. T)*.This implies a scalar quantity is the same in all coordinate axes. A vector involves one direction and has a single subscript (Ei , with i= 1,2,3 in 3D, i.e. (E1, E2, E3) or (Ex, Ey, Ez)). A tensor (rank-2) has two directions involved and has two subscripts (ij , with i,j = 1,2,3 in 3D). * Note: only one number needed at each point. If there is a to point to point variation of temperature a set of T have to be specified for each (x,y,z) which gives rise to the temperature field. Rank n (2D) n (3D) Field Tensors 0 1 1 Temperature 1 2 3 2 4 9 Electric field, Magnetic field Stress field, Strain field 3 8 4 16 Property tensors Polar Axial Specific heat Rotatory power Pyroelectricity Pyromagnetism Thermal expansion Magnetoelectricity 27 Piezoelectricity Piezomagnetism 81 Elastic Stiffness Piezogyrotropy n- How many numbers need to be specified Vectors and their transformations The direction and magnitude of a vector (vector is a first rank tensor) is same in any coordinate system. Let us consider a vector P in (x,y) coordinate axes with intercepts (Px, Py). Let us consider rotation of axes by an angle (using z-axis) as in the figure below. The new intercepts along the coordinate axes (Px’ ,Py’) can be related to the old ones (x,y) by a transformation matrix (aij). Needless to say the magnitude and direction of the vector remains unchanged during the rotation of the coordinate system only the intercepts (x,y) along the coordinate axes change. The aij are nothing but the direction cosines between the new and the old axes. For a certain specific orientation (=0) the component along y-axis (or for that matter the x-axis) will be zero. Px ' cos sin Px P P sin cos y y' Px ' Cos .Px Sin Py a11Px a12 Py Py ' Sin .Px Cos Py a21Px a22 Py Cos(90 ) a11 a12 Cos aij a a Cos (90 ) Cos 21 22 These equations can be written as: P Px ' a11 a12 Px P P a a y ' 21 22 y Using Einstein’s summation convention Pi ' aij Pj Pi ' aij Pj In this equation ‘i’ is free index and ‘j’ is the dummy index (over which the sum is performed) i=1,2 & j = 1,2 (here the ‘=‘ means ‘takes values of’ ). ‘x’, ‘y’ can also b replaced with indices ‘1’, ‘2’. In 3D the aij will be a 3×3 matrix and the equation using direction cosines (as in table below) can be written as: Px ' a11 a12 P a y ' 21 a22 P a z ' 31 a32 a13 Px The condensed equation (in 3D) a23 Py still remains the same except that i = 1,2,3 & j = 1,2,3 Pi aij Pj a33 P z Direction cosines (3D) x1' x2' x3' x1 a11 a12 a13 x2 a21 a22 a23 Sometimes we need to go from the old to the new coordinate system*. x3 In this case the equations turn out to be: a31 a32 a33 The reverse transformation P1 a11P1' a21P2' a31P3' P2 a12 P1' a22 P2' a32 P3' Pi a ji Pj' P3 a13P1' a23P2' a33P3' * Hey! Can’t I just call the new old and the old new? Note the position of the dummy index now (in aji) Transformation of Tensors As mentioned before there are two kinds of tensors (here we are keeping our focus on 2nd and higher rank tensors): (i) field tensors and (ii) property tensors. Many material/physical properties have a tensorial nature (i.e. are tensors). The effect of symmetry on physical properties can be determined by how the tensor transforms under a symmetry operation. The magnitude of a property in any arbitrary direction can be evaluated by transforming the tensor. As expected, under the action of a symmetry operator of a crystal the Tensor properties do not change. Scalar such as Temperature is same in all coordinates. So, if the temperature is T at a point in space, it is still same whatever coordinates we choose. We have already seen how vectors transform; now let us see how 2nd rank tensors transform (due to coordinate transformation). Let us consider a vector (pi) related to another vector (qj) via a tensor (Tij). [p & q could be fields as we shall see later]. Let p,q be polar vectors for now. p1 T11q1 T12q2 T13q3 p2 T21q1 T22q2 T23q3 p3 T31q1 T32q2 T33q3 In matrix form p1 T11 T12 T13 q1 p T T T q 2 21 22 23 2 p T T T q 3 31 32 33 3 Using Einstein summation convention pi Tij q j ‘i’ is free index and ‘j’ is the dummy index (over which the sum is performed) Continued… We have pi Tij q j (1) The vector pi (or pk) transforms to the new coordinate system as: In terms of the alternate indices (1) can be written as: pi' aik pk pk Tkl ql (2) (3) The vector qi (or qk) transforms to the old coordinate system from new as: ql a jl q'j (4) Putting together equations (2,3,4): p i' aik pk aik Tkl ql aik Tkl ql aikTkl a jl q'j aik a jlTkl q'j That is: p i' aik a jlTkl q'j Now this is nothing but the relation between p and q in the new coordinate system (the ‘’’ system). This implies that the quantity in the brackets must be Tij’ The transformation matrix in the primed coordinate system. Tij aik a jlTkl ‘i,j’ are free indices and ‘k,l’ are dummy indices (over which the sum is performed) Alternate Matrix method for Tensor Transformation We have noted that we can transform 2nd rank tensors using the relation Tij aik a jlTkl A alternate matrix form of this equation is also very useful, which can be derived as below. The relations we have already seen are: Vectors from old to new coordinate system p a p 1 q a q q a q One vector to another in old coordinate system One vector to another in new coordinate system p T q For a orthogonal matrix the transpose is the inverse: (a)T = (a)1 p T q Next we substitute one by one these relations to identify [T’] p a p a T q a T a q a T a q T q 1 T a T a T T Noting that: a T a T a T a T We get: T a T a T Notes on transformation matrices The new set of axes is related to the old set by three direction cosines (3 nos.). This implies that not all the 9 terms in the transformation matrices (aij) are independent and only 3 are independent. This implies that there must be 6 relations between the (aij). As each row in the (aij) matrix represents a direction of a vector with respect to 3 orthogonal axes (i.e as direction cosines), we have three relations of the type: Cos2α+ Cos2β+ Cos2 = 1. a112 a122 a132 1 2 2 2 2 2 2 a32 a33 1 a21 a22 a23 1 a31 As any row represents one of the orthogonal directions, product of any two rows is zero. a11a21 a12a22 a13a23 0 a11a31 a12a32 a13a33 0 a21a31 a22a32 a23a33 0 Determinant of the transformation matrices a11 a12 aij a21 a22 a31 a32 a13 a23 a33 For a transformation that leaves the handedness of +1 an axis unchanged (e.g. a rotation) 1 For a transformation that changes the handedness of an axis (e.g. a inversion or mirror) The determinant of any orthogonal matrix is either +1 or −1. All the matrices associated with symmetry operations (rotations, inversion, mirror) are orthogonal. Transformation of Tensors of all ranks (polar) We can generalize the transformation law to any rank tensor as in the table below. These transformation laws serve as the very definition of these tensors. If these tensors represent physical quantities, it becomes clear that the components of the tensor change (from one coordinate system to another) by the physical quantity itself remains unchanged. E.g. the electric field vector may be represented by a sent of 3 different numbers in two different coordinate systems, however (as obvious) the electric field strength itself remains the same. Confusion may arise in the case of 2nd rank tensors in that they resemble a transformation matrix (both are specified by 9 numbers and can be written as a 3×3 matrix). However, they represent different quantities. Tensors (2nd rank) can be transformed to different axes using these transformation matrices; but (clearly) the transformation matrices themselves cannot be transformed (from one axes set to another). Table-T Rank 0 (scalar) 1 (vector) Values required 2D 3D Transformation law Old New New Old ' = = ' 1 1 2 3 pi aij p j pi a ji pj 2 (*) 4 9 Tij aik a jl Tkl Tij aki alj Tkl 3 8 27 Tijk ail a jm akn Tlmn Tijk ali amj ank Tlmn 4 16 81 aima jn ako alp Tmnop Tijkl Tijkl ami anj aok a pl Tmnop * Causally called a tensor (i.e. when the word tensor is used without specifying the rank, this implies a rank-2 tensor) Polar and axial tensor properties of rank 0, 1, 2, 3 and 4 Symmetry of property & symmetry of a crystal In a amorphous material there is no symmetry at the atomic level. This implies that there is no preferred direction in a glass i.e. glasses are isotropic* (any property measured along any direction will have the same value). On the other hand crystals can be anisotropic (i.e. properties can be direction dependent). It is perhaps obvious that the symmetry of a property should have$ the symmetry of the crystal ($as we shall see soon this is actually ‘at least the symmetry of the crystal’). E.g. for a crystal with 4mm symmetry a property measured along +x will have the same value as that along +y. E.g. if a field is applied along +x and the current is measured along +x (Jx) this will be equal to the current measured along +y (if field is applied along +y). We expect from 4-fold symmetry and inversion centre (mirrors) present: J+x = J+y = Jx = Jy Ey Jy Jx Ex * It is important to note that glasses with no symmetry at the atomic level have the highest symmetry with respect to properties! Neumann principle We have already noted that the symmetry of a property should be equal to that of the crystal. However, a property may have higher symmetry. So the correct statement is: the symmetry of a property can be equal to that or greater than that of the crystal. Other statements of the Neumann principle. Symmetry elements of a physical property of a crystal must include all the symmetry elements of its point group (all its rotational axes, mirror planes, etc.). Examples of a property having a higher symmetry (than the point group symmetry). We will understand the details soon. All properties that can be represented by tensors of rank up to 2 are isotropic for cubic crystals. Electrical conductivity of cubic crystals is isotropic. How to use Symmetry & Neumann principle to determine the number of independent constants in a property tensor? 1) Start with the property tensor (say in matrix form). 2) Reduce the number of independent components based on any constrains out the symmetry of the crystal (e.g. symmetry of the stimulus, response, energy considerations, etc.). List out the independent components at the end of all these considerations. 3) Use the appropriate transformation law based on the rank of the tensor (Table-T). Use alternate matrix based transformation rules where applicable (and easier). 4) Apply the appropriate transformation matrices corresponding to the symmetry operators of the crystal (only the bare minimum symmetry operators need to be used (the generator matrices)). In some cases where direct application of transformation principles are possible, the same can be used (e.g. a 3fold along [111] in cubic crystals takes xy, yz & zx). 5) After the application of each transformation, apply Neumann’s principle. I.e. the transformed components must be equal to the original components. Based on this determined the ‘equal’ components of the property tensor and the zero components. These steps will become clear once we take up some actual solved examples in this chapter. How to understand anisotropy? Let us start with a toy model to ‘visualize’ anisotropy in crystals. If the glass ball is pulled as shown then it will not move along the direction of pull, but will move along the direction as marked. I.e. even if the stimulus is along ‘P’, the response is along ‘A’. P Tension Shear A We can think of two alternate ways to understand anisotropy: The direction of the response is different from the direction of the stimulus (if electric field is applied along ‘S’ direction of a crystal the current may flow along ‘R’). The response may involve other terms than the ‘natural’ expectation due to the stimulus (e.g. if a crystal is stretched along ‘F’, it may shear in addition to being elongated). Funda Check What can happen if we pull, bend or twist an anisotropic crystal? If we pull the crystal it may elongate and shear. If we bend the crystal using pure bending moments, it may bend and twist. If we twist the crystal using pure torsional moments, it may twist and bend. The words in red are not the natural responses to the applied load. In an isotropic material only the green responses will exist. How is that a block of Copper is isotropic (say with respect to its elastic properties)? Origin of isotropy at the level of the microstructure and partial anisotropy in crystalline materials At the level of the crystal structure (in a single crystal), a given property may be isotropic due to Neumann’s principle (e.g. cubic crystals like NaCl). However, isotropy may also arise due to spatial averaging of properties at the level of the microstructure. A single crystal of Cu will be anisotropic with respect to its elastic properties (we will see later that 3 independent elastic constants are required: E11, E12, E44). However, a block of Cu is polycrystalline with multiple grains oriented randomly: thus there is no preferred direction for the Cu block and its elastic properties are isotropic* (we require only two independent moduli: E (Young’s modulus) and (Poisson’s ratio) to describe the its elastic response). In a wire of Cu, the grains may not be oriented randomly and such a material is said to possess crystallographic texture. I.e. in a textured material there is (some degree of) preferential orientation of grains. Texture can develop during rolling, extrusion, wiredrawing, thin film growth, etc. In textured materials, the anisotropy present at the level of the single crystal is partially recovered. Atomic structure level Single crystals Origin of Isotropy Due to Neumann’s principle * Assuming that the block has many many grains and hence all orientations are represented. Microstructure level Also for textured materials Stimulus and Response We can apply various kinds of stimuli on a material (like Force, Electric Field, Magnetic Field, Temperature difference, etc.). These fields may give rise to natural responses (like elongation, electric current or polarization, magnetization, heat flow, etc.). However, we may also get responses which are usually associated with other kinds of stimuli. E.g. the application of pressure may lead to the polarization of the crystal (Piezoelectric effect) or the application of a magnetic field may lead to strain in the material (magnetostriction). A material/physical property connects the stimulus to the response. The stimulus response plot may be linear, non-linear or may even show hysteresis. (As stated before) Crystallographic axes vs Property Axes The crystallographic axis (a,b,c) may or may NOT coincide with the property axis (Z1, Z2, Z3). The property axes are always orthogonal, while the crystallographic axes may or may not be orthogonal. The standard settings are as in the table below. Property axis Z1 Z2 Z3 Cubic a b c Hexagonal a (Z1, Z3) c (6-fold) Tetragonal a b c (4-fold) Trigonal (hexagonal setting) a (Z1, Z3) c (3-fold, [001]) Orthorhombic (c < a < b) a b c Monoclinic (Z2, Z3) b [010] 2-fold or m c Triclinic (Z2, Z3) On (010) (010) c Electrical Properties The response of an electric field on a material can be: (i) motion of charges (electrons or ions), (ii) polarization. In metals electrons flow on the application of an electric field, while in materials like solid electrolytes ions carry the current. Materials which lack free charges are called di-electrics (should have been called dia-electrics, which would have made it consistent with dia-magnetics). In dielectrics, the internal field weakly opposes the external field (like in diamagnetic materials the internal magnetic field weakly opposes the external field). In some crystals the centre of mass of the positive charges does not coincide with the centre of mass of negative charges, leading to a net electric dipole. These crystals are spontaneously polarized in the absence of an external field polar materials. Such crystals lack a centre of symmetry (inversion centre). Polar materials come in two types: (i) those in which the reversal in field direction can reverse the direction of spontaneous polarization (called Ferro-electrics) and (ii) those in which this does not happen. Ferroelectric materials show a hysteresis in the electric fieldpolarization plot. Materials which show hyteresis in stimulus-response plots are called Ferroics (in general). In certain crystals pressure (mechanical stress) can lead polarization (or change in polarization if the crystal already has spontaneous polarization). These materials are termed as Piezoelectric. It is also possible that electric field can lead to mechanical strain in the material this is termed as Inverse Piezoelectric effect. Symmetry and Pyroelectric, Piezoelectric and Ferroelectric Effects 32 point groups Crystal Symmetry Point Groups 21 point groups Noncentrosymmetric Groups 1 point group 432 Possessing Other Symmetry Elements (Nonpolar) Do not show Pyro-, Piezoor Ferroelectric effects 11 point groups Centrosymmetric Groups 20 point groups Piezoelectric Effect (Polarized under Mechanical Stress) 1, 2, m, 222, mm2, 4, 4, 422, 4mm, 42m, 3, 32, 3m, 6, 6, 622, 6mm, 62m, 23, 43m Out of the 20 PG 10 show pyroelectricity Polarized in the absence of an electric field Polar crystals 10 point groups Pyroelectric Effect (Spontaneously Polarized) 1, 2, m, mm2, 3, 3m, 4, 4mm, 6, 6mm Out of the 10 PG a subset show Ferroelectric effect Polar crystals Subgroup of the point groups Ferroelectric Effect (Spontaneously Polarized With Reversible Polarization) Pyroelectricity On heating/cooling in some materials (like tourmaline*, gallium nitride (GaN) based materials, caesium nitrate (CsNO3), Lithium tantalate (LiTaO3, LiNbO3)) voltage develops, this phenomenon is called pyroelectricity. On heating/cooling charge develops on the opposite faces of crystals lacking centre of inversion. Heating leads to shift in atomic positions so as to lead to a voltage. All pyroelectric materials are also piezoelectric, but the vice-versa is not true. The temperature change (T) is related to the polarization (P) by: Pi pi T Pi → polarization vector [C/m2] pi → pyro-electric coefficient (polar first rank tensor/vector property) On heating/cooling in some materials (like tourmaline, gallium nitride (GaN), caesium nitrate (CsNO3), Lithium tantalate (LiTaO3)) voltage develops, this phenomenon is called pyroelectricity. On heating/cooling charge develops on the opposite faces of crystals lacking centre of inversion. As temperature change (stimulus) does NOT have a directionality, the response (polarization) must correspond to the symmetry of the crystal. All pyroelectric materials are also piezoelectric, but the vice-versa is not true. The temperature change (T) is related to the polarization (P) by: ' Pi is a polar vector, which transforms as: Pi aij Pj * Common black tourmaline has a nominal formula NaFe2+3Al6Si6O18(BO3)3(OH)4 0 0 1 0 0 1 The coefficients after the application of the inversion operator is: p1' 1 0 0 p1 p1 ' p 2 0 1 0 p 2 p 2 p3' 0 0 1 p3 p3 p1' p1 ' p2 p2 p3' p3 If a component of a tensor changes sign after a transformation of coordinates, the component must vanish (= 0) for that crystal in accordance with Neumann’s principle. By Neumann’s principle: p1' p1 p1 ' p2 p2 p2 p3' p3 p3 p1 0 p 0 2 p 0 3 Point groups with inversion symmetry not showing pyroelectricity Crystals with centre of symmetry do not show pyroelectric effect. Let the property axes be the orthogonal set (Z1, Z2, Z3) and let the components of the pyroelectric coefficient be: (p1, p2, p3). The matrix operator for centre of inversion is: 1 0 0 Crystal System Group with Centre of symmetry (i) Cubic (2) 4 2 3 m m 2 3 m Hexagonal (2) 6 2 2 m m m 6 m Trigonal (2) 3 2 m 3 Tetragonal (2) 4 2 2 m m m 4 m Orthorhombic (1) 2 2 2 m m m Monoclinic (1) 2 m Triclinic (1) 1 This implies that in all crystals with centre of symmetry pyroelectricity is absent (i.e. if we heat these type of crystals no charge/potential will develop): (i) 11 of the 32 point groups & (ii) 2 out of 7 Curie groups (/m m, m). We have noted that not all crystals which lack an inversion centre are pyroelectric. This implies that not all piezo-electric crystals are pyroelectric. Quartz is a well known piezoelectric crystal, which is not pyroelectric. Quartz has a point group symmetry 32 (2 || Z1 & 3 || Z3). This implies that the pyroelectric coefficients will remain the same under these transformations. Note: all cubic crystals have 2-fold || <001> and 3-fold || <111>. 3 2 0 p1 p1 2 3 p2 2 p1' 1 2 ' 3 p1 p2 3-fold along Z3 2 2 p2 3 2 1 2 0 p 2 p3' 0 0 1 p3 p3 By Neumann’s principle: p1 p1 2 3 p2 2 3 p1 = p2 Both these conditions p 3 p1 p2 are satisfied only 2 2 2 p = 3 p 1 2 if p1 = p2 = 0 p p3 3 Now we apply the other symmetry operation (2-fold along Z1 (after the 3-fold operation) 2-fold along Z1 p1' 1 0 0 0 0 ' p2 0 1 0 0 0 p3' 0 0 1 p3 p3 p1 0 p 0 By Neumann’s principle: 2 p p 3 3 p1 0 p 0 2 p p 3 3 p1 0 p 0 2 p 0 3 It is to be noted that though we are deriving the effect of symmetry on the pyroelectric coefficients, it is applicable to all 1st order tensor (vector) properties (as there is nothing specific to pyroelectricity in the matrix operations). Now let us look at the tourmaline crystal, which addition to being pyroelectric is piezoelectric. Tourmaline has a point group symmetry 3m (m Z1 & 3 || Z3). This implies that the pyroelectric coefficients will remain the same under these transformations. m Z1 p1' 1 0 0 p1 p1 ' p2 0 1 0 p2 p2 p3' 0 0 1 p3 p3 By Neumann’s principle: p1 p1 p2 p 2 p p 3 3 p1 0 p p 2 2 p p 3 3 3 2 0 0 3 p2 2 p1' 1 2 ' p2 p 3 2 1 2 0 p 3-fold along Z3 2 2 2 ' p3 0 0 1 p3 p3 p1 0 p2 0 Since p3 survives tourmaline is pyroelectric p p 3 3 3 p2/2 = 0 p2 = p2/2 p2 = 0 Polar axis The direction of polarization (polar axis) is determined by the symmetry of the crystal. If the polarization can be visualized as an arrow mark (), the ends of the arrow cannot be related by any symmetry operator of the crystal. The disawllowed operations are as below. As expected pyroelectricity always occurs along a polar axis, this does not imply that all polar axis will show pyroelectricity. E.g. Z1 axis of quartz (32 symmetry) is a polar axis (along ‘a’ direction in hexagonal setting of the trigonal crystal), however, pyroelectric charges do not accumulate along this direction. This happens due to the presence of the 3-fold orthogonal to the Z1 (which implies that there will be three equivalent directions 120 apart which will lead to zero net polarization). How to locate the Polar axis? If vectors are drawn from the origin to each of the equivalent points and the resultant obtained, this will be along the polar direction. Examples are shown for point groups m and 2. If the vectoral sum leads to a zero resultant then there will be no net polarization and hence no polar direction. E.g. for the point group 2/m. Pyroelectricity in cubic materials All cubic crystals have 2-fold || <001> and 3-fold || <111>. 3-fold along <111> will take xy, yz & zx. 3-fold along [111] p1' 0 1 0 p1 p2 ' p2 0 0 1 p2 p3 p3' 1 0 0 p3 p1 By Neumann’s principle: p1 p2 p2 p3 p p 3 1 p1 p1 p p 2 1 p p 3 1 Now we apply the other symmetry operation (2-fold along Z1 (after the 3-fold operation) 2-fold along Z1 p1' 1 0 0 p1 p1 ' p2 0 1 0 p1 p1 p3' 0 0 1 p1 p1 By Neumann’s principle: p1 0 p 0 2 p 0 3 It is to be noted that though we are deriving the effect of symmetry on the pyroelectric coefficients, it is applicable to all 1st order tensor (vector) properties (as there is nothing specific to pyroelectricity in the matrix operations). In cubic crystals first rank tensor properties vanish. Pyroelectricity in textured materials Suppose we are not considering a single crystal but a material with texture with m symmetry (a strong electric field along Z3, which aligns domains parallel to Z3). Will pyrolectricity survive in the textured material? || Z3 p1' Cos ' p2 Sin p3' 0 Sin Cos 0 0 p1 p1 Cos p2 Sin 0 p2 p1 Sin p2 Cos 1 p3 p3 p Cos p2 Sin p1 If equality in row-1 and By Neumann’s principle: 1 p p Sin p Cos 1 2 2 row-2 are to be applicable p for all values p3 3 m Z1 p1' 1 0 0 0 0 ' 0 0 p 0 1 0 2 p3' 0 0 1 p3 p3 p1 0 p 0 2 p p 3 3 Since p3 survives the textured material with m symmetry is pyroelectric p1 0 p 0 2 p p 3 3 Pyroelectric crystal classes We have noted that there are 10 points groups, which show pyroelectricity. Two Curie groups also show pyroelectricity. These are listed below. The number of independent measurements required is the number of non-zero coefficients in each case. Point groups Curie Groups Pyroelectric coefficients 1 p1 p 2 p 3 (3 Nos.) 2 0 p 2 0 (1 No) m p1 0 p 3 (2 Nos.) mm2 (OR), 3, 3m (Trigonal), 4, 4mm (Tetragonal) 6, 6mm (Hexagonal) 0 0 p 3 (1 No) , m Number of independent values required Ferroelectricity With special reference to Perovskites BaTiO3 (a model material w.r.t to ferroelectricity) has a cubic structure with centre of symmetry above 120C and hence has no permanent dipole moment. Below 120C the crystal structure is tetragonal, with the ‘Ti’ shifted from the centroid of the octahedra formed by ‘O’. This is an example of a Perovskite structure, which have a general formula ABO3 (other examples are: SrTiO3, KTaO3, SrSnO3, and many more). In fact BaTiO3 [(Ba+2Ti+4) (O2)3] can exist in hexagonal, cubic, tetragonal, orthorhombic, and rhombohedral crystal structures. All of these phases exhibit the ferroelectric effect except the cubic phase (with an inversion centre). Not all Perovskites are ferroelectric, SrTiO3 (at RT) with centre of symmetry is cubic (cP5, Pm3m) and is not a ferroelectric material. In BaTiO3 the Ti+4 ion is slightly smaller than the space given by the octahedral position and hence the ion slightly shifts along one of the <001> directions; thus lowering the symmetry of the crystal to tetragonal. This further introduces a permanent dipole to the structure. Note: SrTiO3 becomes tetragonal at low T (below 168C). Regions within the material where the electric dipoles are parallely oriented (say along [001]) form a ferroelectric domain. In neighbouring domains the dipole may be oriented along one of the other members of the <001> family (e.g. [010]). Different Perovskites can exhibit a variety of properties like they can be: dielectric (CaTiO3), ferroelectric (BaTiO3), piezoelectric (Pb(Zr,Ti)O3), semiconducting ((Ba,La)TiO3), superconducting, etc. (they can even show GMR effect). It is to be noted that some of these compounds have alloying in one of the sublattices and some depend on off-stoichiometry for their properties. BaTiO3 The structure below 120 is tetragonal (next slide for figures and data) with the Ti+4 ion slightly displaced towards one of the <001> directions. BaTiO3 Ti not at the centre of the cell (slightly displaced up) O Ti Ba BaTiO3 Lattice parameter(s) a = 3.99 Å, c = 4.033 Å Space Group P4mm (99) Strukturbericht notation Pearson symbol Other examples with this structure tP5 Wyckoff position Site Symmetry x y z Occ Ba 1a 4mm 0 0 0 1 Ti 1b 4mm ½ ½ 0.515 1 O1 1b 4mm ½ ½ 0.025 1 O2 2c 2mm. 0 ½ 0.483 1 The displacement of Ti gives BaTiO3 a net electric dipole SrTiO3 Ti not at the centre of the cell (unlike in BaTiO3) O Ti Sr SrTiO3 Lattice parameter(s) a = 3.90 Å Space Group Pm3m (221) Strukturbericht notation Pearson symbol Other examples with this structure cP5 Wyckoff position Site Symmetry x y z Occ Ti 1a m3m 0 0 0 1 Sr 1b m3m ½ ½ ½ 1 O 3d 4/mm.m ½ 0 0 1 Piezoelectricity Thermal Expansion When a material is heated it usually expands* (conversely a material will contract on cooling). The strains introduced are stress free strains (i.e. the body will be stress free in the expanded state, in the absence of any external constraints). Since the stimulus (T) has no directions involved, the response (thermal strains) must correspond to the symmetry of the crystal. This implies that none of the symmetry elements of a crystal can be destroyed during free thermal expansion. Thermal expansion (strains) can be related to the temperature change by: 2nd rank tensor (field) ij ij T Scalar Thermal expansion coefficient 2nd rank tensor (material property) Written in full 11 12 13 11 12 13 .T 21 22 23 21 22 23 31 32 33 31 32 33 As strain is a symmetric tensor**, so is the tensor representing the coefficient of thermal expansion. Note that the strain components are scaled-up versions of the coefficients of thermal expansion (with appropriate change in units). * Examples to the contrary exist (in some materials coefficient of thermal expansion may be negative in some temperature regimes). ** In usual materials. Thermal strains along principal directions The directions of principal strains will coincide with the principal directions of αij. Along the principal directions the strains are: 1 1 T 2 2 T 3 3 T This implies that a sphere in the crystal will become an ellipsoid (the strain ellipsoid) on heating/cooling. This is illustrated in the 2D example below, wherein the new lengths along x1 & x2 are: (1+α1T) & (1+α2T). heat The coefficient of bulk expansion is: (α11 + α22 + α33) = (α1 + α2 + α3) is an invariant. Isotropic versus anisotropic thermal expansion In a isotropic material: α11 = α22 = α33 (& α12 = α23 = α31 = 0)*. To understand the effect of isotropic expansion (in 2D) let us consider a unit square which is randomly oriented w.r.t to the principal axes (x1, x2). Before and after thermal expansion (as the green circle goes to the red circle) the square (yellow) remains a square (pink). Fig.1: Isotropic expansion In the case of an anisotropic crystal (in 2D), α11 α22 & hence 11 22. In such a crystal on thermal expansion the green circle becomes the red ellipse and a square (yellow in Fig.2) becomes a parallelogram (pink) after thermal expansion. * We will soon see “why?”. Fig.2: Anisotropic crystal Circular hole remains circular Isotropic Anisotropic Circular hole becomes ellipse Symmetry imposed restrictions on the number of independent coefficients We have noted before that axes transformations can be carried out by: T a T a T Let us consider a cubic crystal with (4/m 3 2/m) symmetry (highest available for cubic crystals) 11' 12' 13' 0 1 0 11 12 13 0 1 0 ' 1 0 0 ' ' 1 0 0 21 22 23 21 22 23 ' ' ' 31 32 33 0 0 1 31 32 33 0 0 1 4-fold along Z3 Like in tetragonal crystals By Neumann’s 11 principle: 21 31 0 1 0 12 11 13 22 1 0 0 22 21 23 12 0 0 1 32 31 33 32 12 13 22 21 23 22 23 12 11 13 32 33 32 31 33 21 23 11 13 31 33 0 11 12 13 11 0 0 0 22 23 11 21 31 32 33 0 0 33 If a crystal had only a 4-fold axis then, two independent coefficients would survive: α11 & α33. This implies that all tetragonal crystals have only two independent coefficients (out of a possible 6). It is to be noted that though we are deriving the effect of symmetry on the thermal expansion coefficients, it is applicable to all 2nd order tensor properties (as there is nothing specific to thermal expansion coefficient in the matrix operations). Now we apply the other symmetry operation m Z3 (after the 4-fold operation) m Z3 11' 12' 13' 1 0 0 11 0 0 1 0 0 ' 0 1 0 0 ' ' 0 1 0 0 21 22 23 11 ' ' ' 31 32 33 0 0 1 0 0 0 0 1 33 0 11 1 0 0 11 0 0 1 0 0 11 0 0 0 0 1 0 0 33 0 11' 12' 13' 0 3-fold || [111] ' 1 ' ' 21 22 23 Which is present in all ' ' ' 31 32 33 0 cubic crystals 0 0 1 0 11 0 33 1 0 0 0 0 11 0 0 1 0 0 0 33 0 0 11 0 0 0 33 We got no reduction in the number of coefficients based on the mirror plane. Now we try the 3-fold along [111]. 0 1 11 0 0 0 1 0 0 0 0 11 0 0 0 1 1 0 0 0 33 1 0 0 0 0 By Neumann’s principle: 0 11 0 11 12 13 11 0 0 0 22 23 11 0 11 21 31 32 33 0 0 11 This implies that for (4/m 3 2/m) crystals there is only one independent coefficient. We could have change the order of the operations (i.e. we could have operated the 3-fold first) and this should not make any difference. Also, we could have operated the 3 instead of the 3-fold (as this is available for the (4/m 3 2/m) crystals. Next, we ask the question: “how many independent coefficients will a second rank tensor property have for cubic crystals”. This includes cubic crystals lower point group symmetry like ’23’. All cubic crystals have a 3-fold || to <111> and 2-fold || <100>* Now let us try the other option pointed out before; i.e. operate the 3-fold axis first. 3-fold || [111] 11' 12' 13' 0 0 1 11 12 13 0 1 0 ' 1 0 0 ' ' 0 0 1 22 23 22 23 21 21 ' ' ' 31 32 33 0 1 0 31 32 33 1 0 0 0 0 1 11 12 13 0 1 0 0 0 1 13 11 12 33 31 32 1 0 0 21 22 23 0 0 1 1 0 0 23 21 22 13 11 12 0 1 0 1 0 0 0 1 0 33 31 32 23 21 22 31 32 33 By Neumann’s 11 12 principle: 22 21 31 32 13 33 31 32 23 13 11 12 33 23 21 22 α11 = α22 = α33 α12 = α13 = α23 11 12 13 11 12 12 22 23 11 12 21 12 31 32 33 12 12 11 * Note: not all cubic crystals have 4-fold || <100>. In addition, cubic crystal may have 2-fold || <110> Next we operate the 2-fold || [001] 2-fold || [001] 11' 12' 13' 1 0 0 11 12 12 1 0 0 ' 0 1 0 ' ' 0 1 0 21 22 23 12 11 12 ' ' ' 31 32 33 0 0 1 12 12 11 0 0 1 1 0 0 11 12 12 11 0 1 0 12 11 12 12 0 0 1 12 12 11 12 By Neumann’s 11 12 principle: 12 12 12 11 12 12 11 12 12 11 12 11 12 12 12 12 11 12 11 12 12 11 α12 = 0 0 11 12 13 11 0 0 0 21 22 23 11 31 32 33 0 0 11 All cubic crystals are isotropic with respect to second rank tensor properties (require only one independent constant). Centrosymmetry in 2nd rank tensor properties Let us consider a vector stimulus qj connected to a vector response pi via a tensor property Tij. Let us reverse the direction of the stimulus, this will reverse the direction of the response without affecting Tij. This implies that all second rank tensor properties are centrosymmetrical. pi Tij q j Tij q j Tij q j pi p1 T11 T12 T13 q1 p T T q T 2 21 22 23 2 Reversing stimulus p T T T q 3 31 32 33 3 p1 T11 T12 T13 q1 p T T q T 2 21 22 23 2 p T T T q 3 31 32 33 3 The effect of crystal symmetry on properties represented by symmetrical second-rank tensors Optical classifica tion System Characteristic symmetry[1] Nature of representation quadric and its orientation Number of independent coefficients Cubic Four 3-fold axes Sphere 1 S 0 0 0 S 0 0 0 S Tetragonal One 4-fold axis 2 Hexagonal One 6-fold axis Trigonal One 3-fold axis Quadric of revolution about the principal symmetry axis x3 z S1 0 0 0 S1 0 0 0 S3 Orthorhombic Three mutually perpendicular 2-fold axes; no axes of higher order General quadric with axes x1, x2 , x3 to the diad 3 S1 0 0 0 S2 0 0 0 S3 One 2-fold axis General quadric with one axis x2 to the diad 4 S11 0 S31 0 S2 0 S31 0 S33 General quadric. No fixed relation to crystallographic axes 6 S11 S 12 S31 S12 S22 S23 S31 S23 S33 Isotropic (anaxial) Uniaxial Tensor[2] Monoclinic axes x, y, z axis y Biaxial Triclinic A centre of symmetry or no symmetry [1] Axes of symmetry may be rotation axes or inversion axes. [2] The setting of the reference axes x1 , x2 , x3 in column 6 in relation to the crystallographic axes x, y, z and to the symmetry elements is that shown in column 4. 4th Order Tensor Properties (mechanics) The stresses are related to strains by Hooke’s law via the 4th order tensor properties: Stiffness (Eijkl) and Compliance (Sijkl). Note: Usually ‘C’ is the symbol for stiffness and the symbol for compliance is not ‘C’ and confusing with ‘Stiffness’! ij Eijkl kl ij Sijkl kl Being 4th order tensors there are 3×3×3×3 (= 81) components (in 3D). Not all these components are independent. The number of independent components reduces 81 to 36 given that stress and strain are symmetric tensors. For diagonal terms: 11 S111212 S1121 21 is a symmetric tensor: 12 21 11 ( S1112 S1121 )12 S1112 & S1121 always occur together and cannot be experimentally separated and keeping this in view S1112 is assumed to be equal to S1121. For off-diagonal terms: 12 ( S1233 ) 33 21 ( S2133 ) 33 Eij kl 9×9 If all components are independent As 12 = 21 As ‘ij’ & ‘kl’ refer to strain & stress tensors which have 6 independent components (3D) S2133 S1233 Eij kl 6×6 Thus not all components are independent The single index notation for stress & strain Voigt’s notation Sometimes the indices are condensed (from 2 to 1) according to the notation as below. The two index notation is the matrix notation and has to be converted back to tensor notation so that transformations can be carried out (as usual for tensors). 11 12 13 1 6 5 22 23 2 4 33 3 Tensor Matrix 11 12 13 1 22 23 33 1 6 1 6 6 dW i d i Eij j d i 2 i 1 2 j 1 i 1 5 1 2 4 3 1 2 Only one symmetric half of the matrix is written Matrix Tensor 1 E11 This will lead to condensed notation 2 E21 version of the stress-strain relation 3 E31 (matrix form) 4 E41 5 E51 E.g. E43 E2333 6 E61 6 2 1 2 E12 E22 E32 E42 E52 E62 E13 E23 E33 E43 E53 E63 E14 E24 E34 E44 E54 E64 E15 E25 E35 E45 E55 E65 E16 1 E26 2 E36 3 E46 4 E56 5 E66 6 Further reduction in the number of independent moduli is possible using the concept of strain energy of a hyper-elastic material. If ‘W’ is the strain energy per unit volume: 1 3 3 1 3 3 dW ij d ij Eijkl kl d ij 2 i 1 i 1 2 i 1 i 1 Let us consider the specific case where the only stress applied is 11 (= 1 in condensed index notation) and the body is in plane strain condition (i.e. 13, 23 & 33 are zero). The strain energy is given by (Taylor series expansion for small strain in a hyperelastic material): 2 1 W 1 W W ( ij ) W (0) ij ij kl ... 1 ij 2 ij kl 0 0 i j i j W ( ij ) W (0) ij ij T 3 ... Ignoring higher order terms and observing that the quantity in blue font is Eijkl Zero if no residual strain Zero if no residual stress Noting that the order of differentiation does not matter 2 2 1 W 1 1 W 1 W ( ij ) E ijkl ij kl 2 ij kl 2 Eklij ij kl ij kl 2 ij kl 2 ij 0 kl ij ij 0 E E ijkl klij Eijkl is a symmetric tensor Effect of symmetry elements on Eijkl We have noted that even for crystals without any symmetry, only 21 of the 81 possible elastic constants are independent. For crystals with symmetry this number is further reduced. Let us consider a tetragonal crystal with 4 symmetry. The 4-fold will take: (a)(b), (b)(a), (c)(c). Matrix of surviving coefficients is shaded blue only 7 independent terms survive: E1111, E3333, E1122, E1133, E1313, E1212, E1112. 1111 1122 1133 1123 1131 1112 2222 2233 2223 2231 2212 3333 3323 3331 3312 2323 2331 2312 3131 3112 1212 2222 2211 2233 2213 2232 1111 1133 1113 1132 3333 3313 3332 1313 1332 3232 1131=1113=2223=2232=1113 all these coefficients are zero 2213=1123=1132=2231=2213 all these coefficients are zero 3331=3332=3323=3313=3331 all these coefficients are zero 2312=3221=1321=3112=3221 all these coefficients are zero 2221 1121 3321 1321 3221 2121 0 0 1112 1111 1122 1133 1111 1133 0 0 111 2 3333 0 0 0 4 fold Eijkl 1313 0 0 1313 0 1212 3312=3321=3312 all these coefficients are zero 2331=1332=3213=2331 all these coefficients are zero Components of Eijkl for cubic crystals Cubic point groups 23, 43m, 2 4 2 3, 432, 3 m m m Cubic crystals belong to one of the 5 point groups as above. All the point groups have at least a 3-fold symmetry (along <111>) along with at least a 2-fold along <100>. The 2-fold (along <100>) will take: (a)(a), (b)(b), (c)(c). The 3-fold (along <111>) will take: (a)(b), (b)(c), (c)(a). In the end we have only 3 independent terms: E1111 , E1122 , E2323. In 2-index notation: E11, E12, E44. 1111 1122 1133 1123 1131 1112 2222 2233 2223 2231 2212 3333 3323 3331 3312 2323 2331 2312 3131 3112 1212 0 0 1111 1122 1133 2222 2233 0 0 3333 0 0 2323 2331 3131 Action of 2-fold 1112 2212 3312 0 0 1212 1111 1122 1133 1123 1131 1112 2222 2233 2223 2231 2212 3333 3323 3331 3312 2323 2331 2312 3131 3112 1212 Action of 3-fold 0 0 2223 2222 2233 2211 3333 2233 0 0 3323 1111 0 0 1123 3131 3112 0 1212 0 2323 We see that some of the terms are equal to one another. We have already noted that some of these terms are zero. Hence, the surviving terms (in the symmetric half) are : Note: the total number of non-zero terms is 12 out of possible 36 (24 zero terms). But, only 3 are independent. 0 0 0 1111 1122 1122 1111 1122 0 0 0 1111 0 0 0 2 3 23 0 0 2323 0 2323 Pathway for reduction of number of independent Eijkl 81 Due to symmetry of stress and strain tensors 36 Due to strain energy considerations 21 Due to symmetry present in cubic crystals 3 Curie Principle Click here for introduction to Curie groups When certain stimuli lead to certain responses, the symmetry elements of the stimuli should be seen in the response. A crystal subjected to certain stimulus will display only those symmetry elements, which are common to the crystal without the stimulus and the stimulus without the crystal. In terms of groups this can be written as: R crystal with stimulus G cystal symmetry S Stimulus The symmetry of the crystal in the presence of the stimulus is the intersection group of the symmetry of the crystal (in the absence of the stimulus) with the symmetry of the stimulus (in the absence of the crystal). R, G, S are point groups (and not space groups). Let us consider a cubic crystal with 4/m 3 2/m symmetry, which is loaded along [111] direction. The symmetry of the stimulus is m (cylindrical symmetry). The symmetry of the strained crystal is 3m (the common symmetry to both the crystal and the stimulus). To illustrate the Curie principle, let us consider the example of Ammonium Dihydrogen Phosphate (ADP, 42m) subjected to electric filed along the 4 direction of crystal (along [001], with a pure rotation axis of 2-fold). The stimulus (field) has a symmetry of m. The resultant symmetry of the crystal in the presence of the electric field (stimulus) is 2mm. This can be understood as follows: 2-fold is a subgroup of 4. This is common to that between 4 and and survives. The horizontal 2-fold present in 42m is lost as this is not present in m. The surviving symmetry is 2mm as shown and belongs to the orthorhombic class (can also be written as mm2). m 42m 2mm 4 [001]crystal Let us now impose the electric field along other directions and see it effect. 42m [100]crystal 2 [uvw]crystal 42m m along a m || 2 random direction [110]crystal 42m m || m m 1 1 W 1111 2 2W 11 11 ( E11kl kl ) 11 ( E111111 E111212 E1121 21 E1122 22 ) 11 W ( E1122 ) 11 Taking partial derivatives (1st wrt to 22 then wrt 11) 2 22 2W 2 E1122 11 22 Now reversing the order of the partial derivatives (1st wrt to 11 then wrt 22 ) 2 W (2 E111111 E111212 E1121 21 E1122 22 ) 11 2W 2 E1122 2211 2 Since the order of differentiation should not matter as far as the energy density (W) is concerned, (1) = (2). This implies E1122 = E2211. 1 Now we apply m Z3 (after the 3-fold operation) m Z3 11' 12' 13' 1 0 0 11 12 12 1 0 0 ' 0 1 0 ' ' 0 1 0 22 23 11 12 21 12 ' ' ' 31 32 33 0 0 1 12 12 11 0 0 1 1 0 0 11 12 12 1 0 0 1 0 0 11 12 12 0 1 0 12 11 12 0 1 0 0 1 0 12 11 12 0 0 1 0 0 1 12 12 11 0 0 1 12 12 11 incomplete m Z3 11' 12' 13' 1 0 0 11 12 12 1 0 0 ' 0 1 0 0 1 0 ' ' 22 23 11 12 21 12 ' ' ' 31 32 33 0 0 1 12 12 11 0 0 1