Edmonton, Alberta
... nuclei, labelled according to the allowed values of mI, the projection of the dimensionless nuclear spin angular momentum I along B0, for the case where mI = ±½. ...
... nuclei, labelled according to the allowed values of mI, the projection of the dimensionless nuclear spin angular momentum I along B0, for the case where mI = ±½. ...
General Relativity, Black Holes, and Cosmology
... The spacetime algebra 14.1 Spacetime algebra 14.2 Complex quaternions 14.3 Lorentz transformations and complex quaternions 14.4 Spatial Inversion (P ) and Time Reversal (T ) 14.5 How to implement Lorentz transformations on a computer 14.6 Killing vector fields of Minkowski space 14.7 Dirac matrices ...
... The spacetime algebra 14.1 Spacetime algebra 14.2 Complex quaternions 14.3 Lorentz transformations and complex quaternions 14.4 Spatial Inversion (P ) and Time Reversal (T ) 14.5 How to implement Lorentz transformations on a computer 14.6 Killing vector fields of Minkowski space 14.7 Dirac matrices ...
Solid-State NMR Spectroscopy of Unreceptive Nuclei in Inorganic
... systems with important structural motifs, while 115In SSNMR was applied to systems with In in the +1 oxidation state. Extremely broad SSNMR spectra were acquired at field strengths of 9.4 and 21.1 T using frequency-stepped techniques. In all cases, the electric field gradient (EFG) and the chemical ...
... systems with important structural motifs, while 115In SSNMR was applied to systems with In in the +1 oxidation state. Extremely broad SSNMR spectra were acquired at field strengths of 9.4 and 21.1 T using frequency-stepped techniques. In all cases, the electric field gradient (EFG) and the chemical ...
GEOMETRY, TOPOLOGY AND PHYSICS
... In spite of the extensive use of the concepts of topology, differential geometry and other areas of contemporary mathematics in recent developments in theoretical physics, it is rather difficult to find a self-contained book that is easily accessible to postgraduate students in physics. This book is ...
... In spite of the extensive use of the concepts of topology, differential geometry and other areas of contemporary mathematics in recent developments in theoretical physics, it is rather difficult to find a self-contained book that is easily accessible to postgraduate students in physics. This book is ...
Spin–spin coupling tensors as determined by experiment and
... beam experiments is also discussed in this context. Quantum chemical electronic structure calculations provide a theoretical means to study this property. We focus on the developments since the previous review on LCNMR and computational methods, which was written in 1982 [1]. The solid state NMR lit ...
... beam experiments is also discussed in this context. Quantum chemical electronic structure calculations provide a theoretical means to study this property. We focus on the developments since the previous review on LCNMR and computational methods, which was written in 1982 [1]. The solid state NMR lit ...
Lecture Notes 18.5: Lorentz Transformation of EM Fields, the EM
... transformations of E B in going from one IRF(S) to another IRF(S') ??? In the immediately preceding lecture notes, the reader may have noticed some tacit / implicit assumptions were made, which we now make explicit: 1) Electric charge q (like c, the speed of light) is a Lorentz invariant scalar qu ...
... transformations of E B in going from one IRF(S) to another IRF(S') ??? In the immediately preceding lecture notes, the reader may have noticed some tacit / implicit assumptions were made, which we now make explicit: 1) Electric charge q (like c, the speed of light) is a Lorentz invariant scalar qu ...
A Survey of Molecules With Large Nuclear
... spectral analysis will be left to the following chapters, where the presentation of these details has been tailored to the project under discussion. Microwave spectroscopy is the study of the interaction between microwave radiation, which spans the 300 MHz to 300 GHz portion of the electromagnetic s ...
... spectral analysis will be left to the following chapters, where the presentation of these details has been tailored to the project under discussion. Microwave spectroscopy is the study of the interaction between microwave radiation, which spans the 300 MHz to 300 GHz portion of the electromagnetic s ...
VECTORS 1. Introduction A vector is a quantity that has both
... a and b are perpendicular, in which case they are said to be orthogonal, or (2) one (or both) of these two vectors is (are) zero vector(s). Example 4.2. A vector b can be resolved into two component vectors, one parallel to and the other perpendicular to a given unit vector û (Figure 8). The part t ...
... a and b are perpendicular, in which case they are said to be orthogonal, or (2) one (or both) of these two vectors is (are) zero vector(s). Example 4.2. A vector b can be resolved into two component vectors, one parallel to and the other perpendicular to a given unit vector û (Figure 8). The part t ...
Theory of Molecular Nonlinear Optics
... understanding of and a powerful tool for designing new materials [28]. This work combined evolving approaches to quantum chemistry with previously developed sum-over-states approaches to quantum calculations of optical responses [7,29,30]. The field was now poised to take advantage of the profound c ...
... understanding of and a powerful tool for designing new materials [28]. This work combined evolving approaches to quantum chemistry with previously developed sum-over-states approaches to quantum calculations of optical responses [7,29,30]. The field was now poised to take advantage of the profound c ...
chapter 01
... class of physical quantities is called tensors, of which scalars and vectors are special cases. For most of the time, we shall be concerned with scalars and vectors.4 To distinguish between a scalar and a vector it is customary to represent a vector by a letter with an arrow on top of it, such as A ...
... class of physical quantities is called tensors, of which scalars and vectors are special cases. For most of the time, we shall be concerned with scalars and vectors.4 To distinguish between a scalar and a vector it is customary to represent a vector by a letter with an arrow on top of it, such as A ...
VECTOR ANALYSIS
... class of physical quantities is called tensors, of which scalars and vectors are special cases. For most of the time, we shall be concerned with scalars and vectors.4 To distinguish between a scalar and a vector it is customary to represent a vector by a letter with an arrow on top of it, such as A ...
... class of physical quantities is called tensors, of which scalars and vectors are special cases. For most of the time, we shall be concerned with scalars and vectors.4 To distinguish between a scalar and a vector it is customary to represent a vector by a letter with an arrow on top of it, such as A ...
5 General Relativity with Tetrads
... 1. Why tetrads? Because physics is clearer in a locally inertial frame than in a coordinate frame. 2. The primitive object in the tetrad formalism is the vierbein em µ , in place of the metric in the coordinate formalism. 3. Written suitably, for example as equation (1), a metric ds2 encodes not onl ...
... 1. Why tetrads? Because physics is clearer in a locally inertial frame than in a coordinate frame. 2. The primitive object in the tetrad formalism is the vierbein em µ , in place of the metric in the coordinate formalism. 3. Written suitably, for example as equation (1), a metric ds2 encodes not onl ...
Spacetime algebra as a powerful tool for electromagnetism
... We present a comprehensive introduction to spacetime algebra that emphasizes its practicality and power as a tool for the study of electromagnetism. We carefully develop this natural (Clifford) algebra of the Minkowski spacetime geometry, with a particular focus on its intrinsic (and often overlooke ...
... We present a comprehensive introduction to spacetime algebra that emphasizes its practicality and power as a tool for the study of electromagnetism. We carefully develop this natural (Clifford) algebra of the Minkowski spacetime geometry, with a particular focus on its intrinsic (and often overlooke ...
sums, differences and products of vectors
... temperature, work, distance, speed, musical pitch, and electric charge. Values of vector quantities have both size and direction, and this includes such quantities as displacement, velocity, acceleration, force, electric field, and momentum. There are other quantities whose values cannot be represen ...
... temperature, work, distance, speed, musical pitch, and electric charge. Values of vector quantities have both size and direction, and this includes such quantities as displacement, velocity, acceleration, force, electric field, and momentum. There are other quantities whose values cannot be represen ...
Schutz A First Course in General Relativity(Second Edition).
... The student is assumed already to have studied: special relativity, including the Lorentz transformation and relativistic mechanics; Euclidean vector calculus; ordinary and simple partial differential equations; thermodynamics and hydrostatics; Newtonian gravity (simple stellar structure would be us ...
... The student is assumed already to have studied: special relativity, including the Lorentz transformation and relativistic mechanics; Euclidean vector calculus; ordinary and simple partial differential equations; thermodynamics and hydrostatics; Newtonian gravity (simple stellar structure would be us ...
Word Format
... difficult to represent in Cartesian coordinates, it is necessary to be able to write vectors in component form for other coordinate systems. The key thing to remember about component form is that you can represent any vector provided you know the unit vectors for the coordinate system and can determ ...
... difficult to represent in Cartesian coordinates, it is necessary to be able to write vectors in component form for other coordinate systems. The key thing to remember about component form is that you can represent any vector provided you know the unit vectors for the coordinate system and can determ ...
Electrostriction and electromechanical coupling in elastic dielectrics at nanometric interfaces O.P. T
... the increment in the field direction, i.e. along the X3 axis. T110 and T330 are the stresses even in the absence of an external field, however these stresses are independent of the direction in the case of isotropic dielectrics, and it should not be neglected at the interface having a significant nu ...
... the increment in the field direction, i.e. along the X3 axis. T110 and T330 are the stresses even in the absence of an external field, however these stresses are independent of the direction in the case of isotropic dielectrics, and it should not be neglected at the interface having a significant nu ...
Gravitational and Inertial Mass in General Relativity
... fields, is indeed the physical energy-momentum tensor. In the Lagrangian formulation of the Einstein field equations, the source tensor is T (2 / g ) m / g , where m is the Langrangian density for nongravitational matter, and it is not self-evident that this variational derivative equal ...
... fields, is indeed the physical energy-momentum tensor. In the Lagrangian formulation of the Einstein field equations, the source tensor is T (2 / g ) m / g , where m is the Langrangian density for nongravitational matter, and it is not self-evident that this variational derivative equal ...
Gravito-electromagnetic analogies
... Building up on the work in [2], another approach is herein added to the discussion: the exact analogy based on the fields of inertial forces, arising in the context of the 1+3 splitting of spacetime. This approach, which is herein reformulated and suitably generalized, is still not very well known, ...
... Building up on the work in [2], another approach is herein added to the discussion: the exact analogy based on the fields of inertial forces, arising in the context of the 1+3 splitting of spacetime. This approach, which is herein reformulated and suitably generalized, is still not very well known, ...
Backreaction and the Covariant Formalism of General Relativity
... The epoch that started when the universe was about 5 billion years old and lasts until today is sometimes called the dark energy dominated era. This is due to the fact that according to ΛCDM in this epoch the density of dark energy exceeded the density of matter. In the framework of ΛCDM, dark energ ...
... The epoch that started when the universe was about 5 billion years old and lasts until today is sometimes called the dark energy dominated era. This is due to the fact that according to ΛCDM in this epoch the density of dark energy exceeded the density of matter. In the framework of ΛCDM, dark energ ...
Vectors 101
... first um…obviously… use your right hand. Let your fingers point in the direction of A, and wrap your fingers (as if you’re making a fist) through the angle towards B. Your thumb now points in the direction of the cross product. A ...
... first um…obviously… use your right hand. Let your fingers point in the direction of A, and wrap your fingers (as if you’re making a fist) through the angle towards B. Your thumb now points in the direction of the cross product. A ...
Vectors 101
... first um…obviously… use your right hand. Let your fingers point in the direction of A, and wrap your fingers (as if you’re making a fist) through the angle towards B. Your thumb now points in the direction of the cross product. A ...
... first um…obviously… use your right hand. Let your fingers point in the direction of A, and wrap your fingers (as if you’re making a fist) through the angle towards B. Your thumb now points in the direction of the cross product. A ...
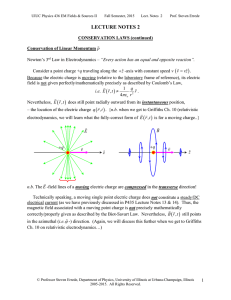
Lecture Notes 02: Conservation Laws (Continued): Conservation of Linear Momentum, Maxwell's Stress Tensor
... n.b. In electrostatics and in magnetostatics, Newton’s 3rd Law of Motion always holds. In electrodynamics, Newton’s 3rd Law of Motion does not hold for the apparent relative motion of two electric charges! (n.b. Isaac Newton could not have forseen this {from an apple falling on his head} because gra ...
... n.b. In electrostatics and in magnetostatics, Newton’s 3rd Law of Motion always holds. In electrodynamics, Newton’s 3rd Law of Motion does not hold for the apparent relative motion of two electric charges! (n.b. Isaac Newton could not have forseen this {from an apple falling on his head} because gra ...