* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Binary Search Trees
Survey
Document related concepts
Transcript
Binary Search Trees
Manolis Koubarakis
Data Structures and Programming
Techniques
1
Binary Search Trees
• Binary search trees are an excellent data structure for
representing sets whose elements are ordered by some
linear order.
• A linear order < on a set 𝑆 satisfies two properties:
– For any 𝑎, 𝑏 ∈ 𝑆, exactly one of 𝑎 < 𝑏, 𝑎 = 𝑏 or 𝑎 > 𝑏 is
true.
– For all 𝑎, 𝑏, 𝑐 ∈ 𝑆, if 𝑎 < 𝑏 and 𝑏 < 𝑐 then 𝑎 < 𝑐
(transitivity).
• Examples of sets with a natural linear order are
integers, floats, characters and strings in C.
Data Structures and Programming
Techniques
2
Definition
• A binary search tree is a binary tree in which
the nodes are labeled with elements of a set.
• Binary search trees have the following
property. For each node N:
Keys in left subtree of N < Key K in node N <
Keys in right subtree of N
• This condition is called the binary search tree
property.
Data Structures and Programming
Techniques
3
Assumption
• We will assume that no two nodes in a binary
search tree have equal keys.
• The assumption can be removed but then
relevant algorithms will be a little bit more
complicated.
Data Structures and Programming
Techniques
4
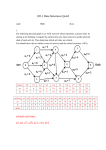
Example
10
14
5
7
18
12
15
Data Structures and Programming
Techniques
5
Example (for the same set)
15
18
14
5
10
7
12
Data Structures and Programming
Techniques
6
Example
ORY
ZRH
JFK
MEX
BRU
ARN
ORD
DUS
GLA
NRT
GCM Data Structures and Programming
Techniques
7
Searching for a Key
• To search for a key K in a binary search tree T,
we compare K to the key Kr of the root of T.
• If K==Kr, the search terminates successfully.
• If K<Kr, the search continues in the left subtree
of T.
• If K>Kr, the search continues in the right
subtree of T.
• If T is the empty tree, the search returns NULL.
Data Structures and Programming
Techniques
8
Type Definitions for Binary Search
Trees
/* This is the file BinarySearchTreeTypes.h */
typedef int TreeEntry;
typedef int KeyType;
/* the types TreeEntry and KeyType depend on
the application */
typedef struct TreeNodeTag {
TreeEntry entry;
struct TreeNodeTag *left;
struct TreeNodeTag *right;
} TreeNode;
Data Structures and Programming
Techniques
9
Searching for a Key
/* TreeSearch: search for target starting at node root.
Pre: The tree to which root points has been created.
Post: The function returns a pointer to a tree node
that matches target or NULL if the target is not
in the tree. */
TreeNode *TreeSearch(TreeNode *root, KeyType target)
{
if (root)
if (target < root->entry)
root=TreeSearch(root->left, target);
else if (target > root->entry)
root=TreeSearch(root->right, target);
return root;
}
Data Structures and Programming
Techniques
10
Inserting a Key
• To insert a key K in a binary search tree T, we
compare K to the key Kr of the root of T.
• If K==Kr, the key is already present in T and the
algorithm stops.
• If K<Kr, the algorithm continues in the left subtree
of T.
• If K>Kr, the algorithm continues in the right
subtree of T.
• If T is the empty tree, then key K is inserted there.
Data Structures and Programming
Techniques
11
Inserting a Key
/* InsertTree: insert a new node in the tree.
Pre: The binary search tree to which root points has been
created. The parameter newnode points to a node that has
been created and contains a key in its entry.
Post: The node newnode has been inserted into the tree in such
a way that the properties of a binary search tree are
preserved. */
TreeNode *InsertTree(TreeNode *root, TreeNode *newnode)
{
if (!root){
root=newnode;
root->left=root->right=NULL;
} else if (newnode->entry < root->entry)
root->left=InsertTree(root->left, newnode);
else
root->right=InsertTree(root->right, newnode);
return root;
}
Data Structures and Programming
Techniques
12
Example
• Let us insert keys e, b, d, f, a, g, c into an
initially empty tree in the order given.
Data Structures and Programming
Techniques
13
Insert e
e
Data Structures and Programming
Techniques
14
Insert b
e
b
Data Structures and Programming
Techniques
15
Insert d
e
b
d
Data Structures and Programming
Techniques
16
Insert f
e
f
b
d
Data Structures and Programming
Techniques
17
Insert a
e
f
b
a
d
Data Structures and Programming
Techniques
18
Insert g
e
f
b
a
d
Data Structures and Programming
Techniques
g
19
Insert c
e
f
b
d
a
g
c
Data Structures and Programming
Techniques
20
Inserting in the Natural Order
• If we insert the previous keys in their natural
order a, b, c, d, e, f, g then the tree
constructed is a chain.
Data Structures and Programming
Techniques
21
Insert a, b, c, d, e, f, g
a
b
c
d
e
f
g
Data Structures and Programming
Techniques
22
Inserting in the Natural Order (cont’d)
• As we will see below, chains result in
inefficient searching. So we should never
insert keys in their natural order in a binary
search tree.
• Similar things hold if keys are in reverse order
or if they are nearly ordered.
Data Structures and Programming
Techniques
23
Example
e
f
b
d
a
g
c
Let us traverse this tree in inorder. What do you notice?
Data Structures and Programming
Techniques
24
Inorder Traversal of Binary Search
Trees
• If we traverse a binary search tree using the
inorder traversal, then the keys of the nodes
come out sorted in their natural order.
• This gives rise to a sorting algorithm called
TreeSort: insert the keys one by one in a
binary search tree, then traverse the tree
inorder.
Data Structures and Programming
Techniques
25
Deletion from a Binary Search Tree
• An algorithm for deleting a key K from a binary
search tree T is the following.
• If K is in a leaf node then delete it and replace the
link to the deleted node by NULL.
• If K is not in a leaf node but has only one subtree
then delete it and adjust the link from its parent
to point to its subtree.
• If K is in a node with both a left and right subtree
then attach the right subtree in place of the
deleted node, and then hang the left subtree
onto an appropriate node of the right subtree.
Data Structures and Programming
Techniques
26
Pictorially: Deletion of a Leaf
Delete x
x
Data Structures and Programming
Techniques
27
Pictorially: Empty Right Subtree
Delete x
y
x
Data Structures and Programming
Techniques
y
28
Pictorially: Empty Left Subtree
Delete x
x
y
y
Data Structures and Programming
Techniques
29
Pictorially: Neither Subtree is Empty
Delete x
z
x
y
z
y
Data Structures and Programming
Techniques
30
Deleting a Node
/* DeleteNodeTree: delete a new node from the tree.
Pre: The parameter p is the address of an actual node (not a copy)
in a binary search tree, and p is not NULL.
Post: The node p has been deleted from the binary search tree and the resulting
smaller tree has the properties required of a binary search tree. */
void DeleteNodeTree(TreeNode **p)
{
TreeNode *r=*p, *q;
/* used to find place for left subtree */
if (r==NULL)
printf("Attempt to delete a nonexistent node from binary search tree\n");
else if (r->right==NULL){
*p=r->left; /* Reattach left subtree */
free(r);
} else if (r->left==NULL){
*p=r->right; /* Reattach right subtree */
free(r);
} else {
/* Neither subtree is empty */
for (q=r->right; q->left; q=q->left)
;
/* find leftmost node of right subtree */
q->left=r->left;
/* Reattach left subtree */
*p=r->right;
/* Reattach right subtree */
free(r);
}
}
Data Structures and Programming
Techniques
31
Deleting a Node Given a Key
/* DeleteKeyTree: delete a node with key target from the tree.
Pre: root is the root of a binary search tree with a node containing key
equal to target.
Post: The node with key equal to target has been deleted and returned. The
resulting tree has the properties required of a binary search tree.
Uses: DeleteKeyTree recursively, DeleteNodeTree */
void DeleteKeyTree(TreeNode **root, TreeNode **keyposition, KeyType target)
{
if (*root==NULL)
printf("Attempt to delete a key not present in the binary search tree\n");
else if (target == (*root)->entry){
*keyposition=*root;
DeleteNodeTree(root);
} else if (target < (*root)->entry)
DeleteKeyTree(&(*root)->left, keyposition, target);
else
DeleteKeyTree(&(*root)->right, keyposition, target);
}
Data Structures and Programming
Techniques
32
Example: Delete z
r
b
a
r
x
b
y
a
x
y
z
Data Structures and Programming
Techniques
33
Example: Delete x
r
b
a
r
x
b
y
a
y
z
z
Data Structures and Programming
Techniques
34
Example: Delete r
r
b
a
x
x
b
y
a
y
z
z
Data Structures and Programming
Techniques
35
Example: Delete r
r
z
c
z
b
a
y
y
x
x
c
b
a
Data Structures and Programming
Techniques
36
Discussion
• The algorithm for deleting a node may result
in an increase to the height of the tree and
make subsequent operations inefficient.
• Can we find a better algorithm?
Data Structures and Programming
Techniques
37
Better Algorithm for Deletion
• If the key K to be deleted is in an interior node N with
two children, then we can find the lowest-valued key
K’ in the descendants of the right child and replace K by
K’.
• This key is in a node N’ which is the successor of N
under the inorder traversal of the tree.
• This node can be found by starting at the right child of
N and then following left child pointers until we find a
node with a NULL left child.
• Of course, we also need to remove node N’ from the
tree. This can be done easily since this node has at
most one (right) child.
Data Structures and Programming
Techniques
38
Better Algorithm for Deletion (cont’d)
• Notice that the highest-valued key among the
descendants of the left child would do as well.
• This key is in a node N’’ which is the
predecessor of N under the inorder traversal
of the tree.
Data Structures and Programming
Techniques
39
Example: Delete 10
10
14
5
7
12
18
13
15
The lowest-valued key among the descendants of 14 is 12. This key will replace 10
In the tree and its current node will be removed.
Data Structures and Programming
Techniques
40
Example: Result
12
5
14
7
18
13
15
Data Structures and Programming
Techniques
41
Example: Delete 10
10
14
5
7
12
18
13
15
Alternatively, we can replace 10 with the highest-valued key among the
descendants of its left child. This is the key 7.
Data Structures and Programming
Techniques
42
Example: Alternative Result
7
14
5
18
12
13
Data Structures and Programming
Techniques
15
43
Complexity Analysis
• The best case for searching in a binary tree is
the case when the leaves of the tree are on at
most two adjacent levels.
• In this case searching takes 𝑂(log 𝑛) time
where 𝑛 is the number of nodes.
Data Structures and Programming
Techniques
44
Best Case Examples
Data Structures and Programming
Techniques
45
Best Case Examples (cont’d)
Data Structures and Programming
Techniques
46
Best Case Examples (cont’d)
Data Structures and Programming
Techniques
47
Complexity Analysis (cont’d)
• The worst case for searching in a binary tree is
the case when the trees are as deep and
skinny as possible. These are trees with
exactly one internal node on each level.
• In this case searching takes 𝑂(𝑛) time where
𝑛 is the number of nodes.
Data Structures and Programming
Techniques
48
Worst Case Example (Left-linear Tree)
Data Structures and Programming
Techniques
49
Worst Case Example (Zig-zag)
Data Structures and Programming
Techniques
50
Worst Case Example (Right-linear)
Data Structures and Programming
Techniques
51
Complexity Analysis (cont’d)
• The average case for searching in a binary tree
is the case when the tree is one from the set
of all equally likely binary search trees, and all
keys are equally likely to be searched.
• In this case searching takes 𝑂(log 𝑛) time
where 𝑛 is the number of nodes.
Data Structures and Programming
Techniques
52
Complexity Analysis (cont’d)
• The complexity of insertion in a binary search
tree is the same as the complexity of search
given that it makes the same comparisons plus
changing a few pointers.
• The complexity of deletion is also similar for
the more clever algorithm that we gave.
Data Structures and Programming
Techniques
53
Discussion
• Balanced binary search trees have very good
search times (𝑂(log 𝑛)). But if the tree gets
out of balance then the performance can
degrade to 𝑂 𝑛 .
• How much does it cost to keep a binary search
tree balanced?
Data Structures and Programming
Techniques
54
Example
5
3
2
7
4
6
Data Structures and Programming
Techniques
55
Inserting Key 1
5
3
2
7
4
6
1
Data Structures and Programming
Techniques
56
Rebalancing
4
2
1
6
3
5
7
• Note that every key was moved to a new
node, hence rebalancing can take 𝑂(𝑛) time.
Data Structures and Programming
Techniques
57
Question
• Is there a way to achieve 𝑂(log 𝑛) search time
while also achieving 𝑂(log 𝑛) insertion and
deletion time in the worst case?
• In the next lecture we will answer this
question positively by introducing another
kind of binary search trees that have this
property, AVL trees.
Data Structures and Programming
Techniques
58
Readings
• T. A. Standish. Data Structures, Algorithms and
Software Principles in C.
– Chapter 9. Section 9.7
• R. Kruse, C. L. Tondo and B. Leung. Data
Structures, Algorithms and Program Design in
C.
– Chapter 9. Section 9.2
• Ν. Μισυρλής. Δομές Δεδομένων με C.
– Κεφ. 8
Data Structures and Programming
Techniques
59