* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 1.3 Functions, Continued
Large numbers wikipedia , lookup
Vincent's theorem wikipedia , lookup
Functional decomposition wikipedia , lookup
Big O notation wikipedia , lookup
Continuous function wikipedia , lookup
Principia Mathematica wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Non-standard calculus wikipedia , lookup
Elementary mathematics wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Dirac delta function wikipedia , lookup
Function (mathematics) wikipedia , lookup
History of the function concept wikipedia , lookup
System of polynomial equations wikipedia , lookup
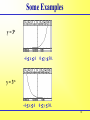
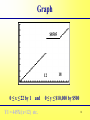
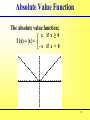
§ 1-3 Functions, Continued The student will learn about: polynomial functions, rational functions, exponential functions, piecewise functions, and difference quotients. 1 Introduction to Polynomials A polynomial function is of the form f (x) = an xn + an-1 xn-1 + … + a1 x + a0 and graphs as a curve that wiggles back and forth across the x-axis. 2 Polynomials f (x) = an xn + an-1 xn-1 + … + a1 x + a0 The coefficients a0, a1, … , an are real numbers with an ≠ 0. The domain of a polynomial function is the set of real numbers. The degree of the polynomial is the highest power of the variable. 3 Polynomial Functions Polynomials are used to model many situations in which change occurs at different rates. For example, the polynomial graphed on the right might represent the total cost of manufacturing x units of a product. At first, costs rise steeply because of high start-up expenses, then more slowly as the economies of mass production come into play, and finally more steeply as new production facilities need to be built. 4 Solving a Polynomial Solutions may be found algebraically. Let f (x) = 0 and solve for x : a. Factor – a bit of work that sometimes requires synthetic division (whatever that is). b. Complete the square – No thank you! c. Use the quadratic formula – Next slide please! d. We will use a graphing calculator and use the calc and zero buttons. I love my calculator! 5 SOLVING A POLYNOMIAL EQUATION BY FACTORING Solve 2x 4 + 4x 3 - 6x 2 = 0 by calculator. Solution: Find the zeros by using your calculator under calc and zeros. Or use table. Introduction to Rational Functions Def: A rational function is any function of the n ( x) form: f ( x) d ( x) where n (x) and d (x) are polynomials. The domain is the set of all real numbers such that d (x) ≠ 0. x2 4x y 2 x 4 Aren’t they pretty? 7 Rational Functions The graphs of these functions are shown below. Notice that these graphs have asymptotes, lines that the graphs approach but never actually reach. The Exponential Function Definition: The equation f (x) = b x for b > 0, b ≠ 1, defines an exponential function. The number b is the base. The domain of f is the set of all real numbers and the range of f is the set of all positive numbers. 9 Some Examples y = 3x -4 x 4 0 y 30. -4 x 4 0 y 30. y = 3-x 10 Piecewise Linear Functions For this example assume that the YCP Tuition is a continuous function. Number of Credits Less than 12 12 to 18 Greater than 18 Cost $505 credit $8505 $8505 plus $505 per credit over 18. Graph this function. Note the points of discontinuity. 11 Graph $8505 12 0 ≤ x ≤ 22 by 1 and Y1 = 445X/(x<12) etc. 18 0 ≤ y ≤ $10,000 by $500 12 Absolute Value Function The absolute value function; f (x) = |x| = x if x ≥ 0 - x if x < 0 13 Difference Quotients In this course it will be important to evaluate the difference quotient for a function: f (x h ) f ( x ) h Given a function - evaluate: 1. f (x + h) ( - ) 2. f (x) 3. f (x + h) – f (x), and finally 4. f (x h ) f ( x ) h 14 Difference Quotients - Example Find the difference quotient for the function f (x h ) f ( x ) f (x) = 4x + 3. Remember h I will call this the 4-step procedure. 1. f (x + h) = 4 (x + h) + 3 = 4x + 4h + 3 ( - ) 2. f (x) = 4x +3 3. f (x + h) – f (x) = step 1 – f (x) = 4h 4. f ( x h ) f ( x ) 4h 4 h h 15 Difference Quotients - Example Find the difference quotient for the function f (x) = x2 + 3x - 4. Remember f (x h ) f ( x ) h 1. f (x + h) = (x + h) 2 + 3(x + h) - 4 ( - ) 2. = x 2 + 2xh + h 2 + 3x + 3h - 4 f (x) = x 2 + 3x -4 3. f (x + h) – f (x) = 2xh + h 2 + 3h 2 f ( x h ) f ( x ) 2xh h 3h 4. 2x h 3 h h 16 Summary. • We learned about polynomial functions. • We learned about the rational functions. • We learned about the exponential functions. • We learned about piecewise linear functions. • We learned about difference quotients. 17 ASSIGNMENT §1.3 Homework on my website 15, 16, 17, 18, 19. 18