Download O star

Astronomy 2
Overview of the Universe
Winter 2006
6. Lectures on Stellar Properties.
Joe Miller
The basic unit of distance is the parsec (pc), which comes
from parallax of a second of arc. The light year is the
distance light travels in one year moving at 300,000 km/sec.
The sun is about eight light minutes away. 1 pc = 3.26 lt. yrs.
The closest star other than the sun is Proxima Centauri with
d=1.30 pc and p=0.772 arcsec.
A star with a distance of 1 pc will have
a parallax of 1 arcsecond, that is, its
position in the sky will shift one
arcsecond over a baseline of 1
astronomical unit (au). This leads to
the basic formula for distance:
1
, where d is in pc
p(")
and p, the parallax, is in arcseconds.
d(pc) 
Measuring the brightness of stars.
Astronomers today still use the scheme developed by
Hipparchus 20 centuries ago! It is a relative system, not
absolute, in that a star’s brightness is compared to the
brightness of standard stars.
The magnitude system:
Hipparchus called the brightest stars in the sky “stars of the
first magnitude” and the faintest stars the eye could see
“stars of the sixth magnitude.” Thus there were five
magnitudes difference between the brightest and faintest stars
(6-1). It turns out that a difference of five magnitudes
corresponds to a ratio of 100 times in brightness or light
output.
5 magnitudes difference = factor of 100 in brightness
Magnitudes (cont.)
Note that magnitudes work backward- the fainter the
star, the bigger the magnitude or number.
1 magnitude difference = factor of 2.5.. in brightness
2
=
2.5 x 2.5 = 6.25
.
5
= 2.5 x 2.5 x 2.5 x 2.5 x 2.5
= 100.
Faintest stars we can detect with largest telescopes
are about magnitude 30! What is brighter than
mag. 1? Mag. 0, and brighter than that you go
negative:
Venus = -4.4, full moon = -12.5, sun = -27.
We have been discussing the apparent magnitude,
which is generally written with the lower case m.
The apparent magnitude is what you observe.
But, m depends on two things: how much light a star
is actually putting out, its intrinsic brightness, and
how far away it is.
In order to study the physical properties of stars,
astronomers must know their intrinsic light output.
Once again, astronomers have set up a relative
system to do this.
Intrinsic brightness of stars
In order to compare the relative amount of light
output of different stars, astronomers have defined a
special kind of magnitude called the absolute
magnitude. It is written with the capital M.
M is the apparent magnitude m a star would have if
it were 10 pc away. In other words, 10 pc has been
chosen as the standard distance at which all stars can
be compared in brightness. If a star is at 10 pc, then
M=m. If a star is not at 10 pc, then one must
calculate the brightness it would have if its distance
were changed to 10 pc. This is done using the
inverse square law of light.
Inverse square law of light.
Brightness falls off as
the observer.
1
2 . where
d
d is the distance to
Example of calculating M from d and m.
Suppose d=100 pc
m= +6
Now we ask: how bright would this star be if we moved it to
a distance of 10 pc? Brightness B goes as
1
B 2
d
In other words, bringing a star 10 times closer makes it 100
times brighter. But remember, a factor of 100 in brightness is
equivalent to a difference of five magnitudes. Therefore a

star would brighten five magnitudes bringing it from 100 pc
to 10 pc, so 6-5=1. The star has an absolute magnitude M =1.
Calculating absolute magnitudes M.
The previous example was based on numbers chosen to work
out simply. In general the problem requires a more
complicated formula involving logarithms:
m-M = 5 log d - 5
where m = the apparent magnitude
M = the absolute magnitude
d = the distance in parsecs
The distance modulus, DM = m-M, is often used as a
measure of distance. For every increase of 0.5 in DM, a star
gets 10 times further away.
The absolute magnitude of the sun is M = +5.
To summarize:
How bright a star really is (its absolute magnitude M)
depends on bright it appears (its apparent magnitude m,
which can be directly measured) and how far away it is.
Once again the central problem of astronomy- distance- is all
important
The Spectra of Stars
In the early 1900’s it was recognized that though
there was a tremendous variety of different kinds of
spectra for stars, many could sorted into specific
groups or classes based on the appearance of the
features in their spectra. Stars typically have
absorption line spectra, and the spectra range from
those having only a few absorption lines to those
with 1000’s of lines.
Annie Jump Cannon developed the Harvard
classification system and classified over 100,000
stars. Later it was realized that these spectral types
could be arranged in a temperature sequence.
How absorption lines are formed
Spectral Types
The original larger collection of spectral types was
ultimately condensed to seven basic ones and
arranged in a temperature sequence as shown:
O, B, A, F, G, K, M
hottest
coolest
The O stars can have surface temperatures as high as
35,000o, while the M stars are in the 3000o range.
The individual types are further subdivided into 10
subclasses, e.g., B0, B1,…B9, A0, A1, etc. Stars are
classified by matching their spectra to standards for
the various spectral types
Line strengths as a function of temperature and
spectral type
Temperature and spectral type
The absorption lines that are used to classify a star
are formed in the atmospheric gases just above the
dense outer region of the sun where the continuous
radiation spectrum emerges from the opaque lower
layers. The temperature in this layer determines two
fundamentally important physical properties of the
material in the gas:
1) The amount that the various atoms are ionized.
2) The amount different atoms or ions are excited,
that is, the extent to which electrons will be found in
excited energy levels in the atoms or ions.
Ionization, excitation, and temperature
• Temperature measures motion, kinetic energy of gas
particles.
• Higher temperature means faster motions, higher energy
per particle.
• Collisions transfer energy to electrons, excite them to
higher levels.
• Higher temperatures, more energetics collisions lead to
more highly excited electrons.
• Higher temperatures, more energetic collisions lead to
greater probability of ionization.
Therefore higher temperature gasses are more highly excited
and more ionized.
How absorption lines are formed
Ionization and excitation equations
Saha’s ionization equation gives the level of ionization of a
given atom as a function of the temperature and density of the
gas plus various physical properties of the atom or ion itself.
Boltzmann’s excitation gives the expected distribution of
electrons in various energy levels of a given atom or ion as a
function of temperature plus various physical properties of
the atom or ion.
Note about excitation and ionization:
Electrons are constantly cascading down to lower energy
levels and then being re-excited to higher levels or out of the
atom in any single atom or ion. The Saha and Boltzmann
equations are statistical. They give you (extremely accurate)
values that you would expect to find if you averaged over a
volume containing millions of atoms or particles.
An additional important remark on spectral
types:
Use the ionization and excitation equations and
assume all stars have the same chemical
composition:
Then the entire range of spectral types is understood
as a temperature sequence. You only need to
change the temperature to get from O-type through
the sequence to M-type.
Colors of stars
You may recall Wien’s Law, which described the
relationship of temperature to wavelength of
maximum light output:
 max
C
 .
T
It can be illustrated as follows:
Astronomers can use filters to measure the
brightness of stars in different wavelength ranges
(different colors) and thus get a color measurement
for stars. This is a quick way to get a rough measure
of the temperature of a star and thus a rough measure
of the spectral type.
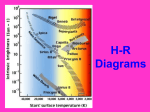
The Hertzsprung-Russell (H-R) Diagram:
Based on two intrinsic properties of stars we can
measure:
1) Intrinsic light output- absolute magnitude
Remember: this requires both apparent magnitude
and distance.
2) Temperature- spectral type.
The H-R diagram is a plot of M vs. spectral type.
A H-R diagram that includes
many visible and nearby stars.
The red line is called the
“main sequence” and is the
location where the vast
majority of stars would be
plotted on the diagram.
Stars in different parts of the H-R diagram are given
different designations (note T across the top):
“Bright giants”
are more often
called
“intermediate
supergiants.”
Ovals indicate
position where
most are found
Complete spectral classification: classification includes
spectral (temperature) class and luminosity class.
1) Spectral class: O, B, A, F, G, K, M
2) Luminosity class: I- supergiants
II- intermediate supergiants
III- giants
IV- sub-giants
V- dwarfs
Examples: Sun G2 V, Antares M2 I, Sirius A0 V
O5 V star, a dwarf, puts out about the same amount of light as
an M2 I supergiant. What is going on here?
Place on the H-R diagram is determined by two
things: temperature and intrinsic brightness or
energy output.
The energy output itself is determined by two things:
1) The energy output per unit area on the surface
of the star.
2) The amount of surface area of the star, that is,
its size.
The surface area of a star is given by A  4R ,
where A is the area and R is the radius of the star.
2
The intrinsic brightness or energy output is
generally called the luminosity, L.
L is determined by the energy output per unit area, E,
times the total area of the star, A. Remember, the
energy output per unit area is given by the StefanBoltzmann equation:
E  T
4
The area is, as we have seen, A  4R 2 ,
and therefore the luminosity L of a star is given by
L  4R T
2
4
Luminosity dependence on radius and temperature:
Let us compare two stars with the full formula:
L1 4R1 2T1 4
R1 2 T14
R1 2 T1 4

 2 4 ( ) ( )
2
4
L2 4R2 T2
R2 T2
R2 T2
L1
R
T
 ( 1 )2 ( 1 )4
L2
R2 T2
Example :
R1  2R2 , T1  2T2

L1
2R
2T
 ( 2 )2 ( 2 )4  (2) 2 (2)4  64
L2
R2
T2
L1  64L2
A supergiant can have the same spectral type and and hence temperature as the
sun, but put out 10,000 times as much light. If it is the same temperature, the only
way it can do this is to have 10,000 times as much area or 100 times the radius.
L1
R
T
R
 ( 1 ) 2 ( 1 ) 4  10,000  ( 1 ) 2 (1), where 1 is the supergiant, 2 is the sun.
L2
R2 T2
R2
R
Taking the square root of both sides, ( 1 )  100.
R2
We have
In like manner, a O star on the main sequence can have the same luminosity as a
red supergiant. Since the O star is roughly 10 times hotter, each unit of surface
area puts out 10,000 times as much energy. To have the same energy output as the
red supergiant, it must have a surface area 10,000 times less, or a radius 100 times
less.

L1
R
T
R
 ( 1 ) 2 ( 1 ) 4  1  ( 1 ) 2 (10) 4 , where 1 is the O star, 2 the supergiant.
L2
R2 T2
R2
R
1
Thus we have ( 1 ) 2  4 . Taking the square root of both sides,
R2
10
R
1
1
( 1) 2 
.
R2 10 100
We have

Thus we see that stellar radius increases diagonally to the upper right in the H-R
diagram.
Now we can see why some stars are called
supergiants
and others
dwarfs.
Luminosity indicators:
The degree of ionization is determined by the
(1) temperature and (2) the density or pressure (pressure is
proportional to density times temperature). A higher density
at the same temperature leads to a lower ionizationrecombination goes faster- while the converse is true at lower
density. Because supergiants are so large compared to
dwarfs, their surface gravities are lower and hence their
atmospheric pressures and densities are lower. This leads to
higher ionization at the same temperature. Certain spectral
lines are quite sensitive to density and pressure and can be
used to distinguish among supergiants, giants, and dwarfs.
An experienced spectroscopist can classify both the
spectral type and the luminosity class of a star from
its spectrum. This is extraordinarily valuable, as it
means that, just from the spectrum of a star, one can
plot it in on the H-R diagram.
BUT: if you can plot a star on the H-R diagram,
you know its absolute magnitude! And if you
know its absolute magnitude and how bright it
appears, its apparent magnitude, then you can
calculate its distance!!
This is called the method of spectroscopic
parallaxes, which is a silly name. It would better be
called the method of spectroscopic distances.
The calibration of the full H-R diagram: clusters
to the rescue!
• Many stars of many spectral types have examples close
enough to get distance from parallaxes.
• Some types of stars are rare, e.g., O stars, M supergiants,
there are no nearby examples, and hence no parallax
distances.
• Not possible to derive absolute magnitudes for these rarer
stars without direct distance measures.
• But…many stars are found in clusters.
• Clusters small, so can assume all the stars in them to be at
the same distance.
Cluster main sequence fitting: by using overlapping
parts of the main sequence of different clusters, it is
possible to calibrate the absolute magnitudes of rarer
stars only found in distant clusters.
Masses of stars
Masses of stars are derived from observations of binary stars, stars in
orbit around one another. The fundamental idea is to use Kepler’s Third
law as modified by Newton:
(M1  M2 )P 2  a 3
If the period of the binary is measured in earth years and the orbital size is
measured in astronomical units (au), then the masses will be in terms of
the sun’s mass.
To measure the size of the orbit in au requires a knowledge of the
distance.
However, this only gives the sum of the masses. To get the individual
masses, one must find out something about the position of the center of
mass or motion with respect to the center of mass of the system. This will
give the ratio of the masses and allow one to compute the masses
individually.
Types of binary stars:
I) Visual binaries- you see both stars.
Orbit of visual binary
Actually the two stars orbit around a center of mass:
II) Spectroscopic binary stars- these stars appear as a single
star because they too close together to be seen as two from
the earth. They reveal their binary nature by periodic Doppler
shifts of their spectral lines as they orbit one another. They
come in two kinds:
1) Single-line. In this case the spectrum of only one star is
visible, and its velocity changes as it goes around its orbit.
2) Double-line. In this case spectral lines from both stars are
visible.
Radial velocity curves:
Double-line binary (cont):
From the period and the velocities we can derive the circumferences and
hence the actual sizes of the orbits.
The relative velocities tell us the ratio of the masses, and thus we have
everything we need to calculate the individual masses.
Not quite! We don’t know the inclination of the orbital plane to the line of
sight.
If the orbits are seen edge-on, then we see the full velocity.
If we were to observe the binary from a direction perpendicular to the
orbit plane, we wouldn’t see any shift at all: the orbital velocities would be
across the line of sight, not along it.
Since there is no way to determine the inclination of the orbital plane, we
only have a rough estimate of the mass, or at best, a statistical estimate.
Unless…the orbit is edge-on and the stars eclipse one-another!!
Double-line eclipsing binary stars- the answer to an
astronomer’s dream.
Now we have:
• The radial velocity curve for each star.
• We know the inclination- the orbit is effectively
edge-on.
• We know the time it takes for various things to
happen:
– The period of mutual revolution.
– The time it takes for each star to go from the
beginning of an eclipse to a complete eclipse.
– The time a star spends in eclipse (transit).
From this we can derive
•
•
•
•
The masses of the individual stars.
The radius of each star.
The shapes (eccentricity) of the orbits.
Sometimes something about the shapes of the stars
or distribution of brightness on the surfaces of the
stars.
Stars can be tidally distorted or have hot spots:
The result: a clearly-defined relationship between
mass and luminosity for main sequence stars.
The-mass luminosity relationship:
LM
3.5
Another way of looking at this:
The conclusion:
The main sequence is a sequence of stars on the H-R
diagram that all share the same chemical composition but
differ in mass. It appears that mass alone may determine
where a star is located along the main sequence.
But this isn’t the whole story!
What about stars that are not on the main sequence?
What is their relationship to main-sequence stars, if any?
The answers to these and related questions have been known
for less than fifty years and require an understanding of the
internal structure and evolution of stars. That is our next
topic.