* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Properties of Circles
Lie sphere geometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Perceived visual angle wikipedia , lookup
Euclidean geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
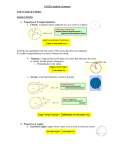
Properties of Circles 1. Definition An inscribed angle is an angle whose vertex is on a circle and each of whose sides intersects the circle in another point. Thus in Figure 1, ! A is an inscribed angle of the circle O(r) with centre O and radius r. It is said to intercept the arc BC and to be inscribed in the arc BAC. Note that these two arcs make up the entire circle. A B minor arc O O O A B B C minor arc C Fig.1 C Fig.2 Fig.3 2. By definition, a central angle is equal in measure to the arc of the unit circle that it intercepts: its minor arc. See Figure 2 where the angle ! BOC has for its measure the arc BC. 3. An inscribed angle is equal in measure to half its intercepted arc. Thus in Figure 3, the angle ! BOC = 2! BAC, or in other words, ! BAC = 1/2 the measure of the arc BC. To show this, let us first consider two chords AB and AC of a circle O(r) where O lies on the chord AB as in the next figure. We want to show that the angle at A, ! A, equals one-half the central angle ! BOC. A C A O B O C B D Because the radii OA and OC are equal, !OAC is an isosceles triangle with ! OCA = ! A. Thus ! A + ! A + ! AOC = π and ! BOC + ! AOC = π also. Subtracting, we find that 2! A = ! BOC and so the inscribed angle ! A is one-half the central angle ! BOC. Now consider the case where O does not lie on AB. Let AO intersect the circle in the point D. Then from above, ! BAD = 12 ! BOD and ! DAC = 12 ! DOC. Together, ! BAC = 1 ! BOC as required 2 This immediately gives us the result that two angles which are inscribed in the same arc of a circle are equal. Thus for example, in Figure 7 below ! P " QQ" = ! P " P Q" 1 because they are inscribed in the same arc of the circle. 4. A quadrilateral is concyclic (i.e. the four vertices lie on the circumference of a circle) if and only if its opposite angles are supplementary, i.e. their sum is π (or 180 degrees). That the opposite angles of a concyclic quadrangle are supplementary is an easy consequence of 3 above, because ! BAD is 12 the measure of the arc BCD, i.e. 12 ! BOD, and similarly ! BCD is 12 the measure of the arc BAD. Since these two arcs add up to 2π, we must have ! A + ! C = 2π. A E D D A O O C B C B Conversely, suppose ABCD is a quadrilateral whose opposite angles are supplementary but the quadrangle is non-concyclic, i.e. the four points A, B, C, D do not lie on the circumference of a circle. Since the three non-collinear points B, C, D determine a circle, let the side BA intersect the circle in E. Then quadrangle EBCD is concyclic, and so ! E + ! C = π. But ! A + ! C = π and so ! E = ! A. But ! A is the exterior angle of the triangle EAB and so must be greater than ! E. This contradiction shows that ABCD is a concyclic quadrangle. 5. If in a circle two lines cut each other, the rectangle contained by the segments of the one is equal to the rectangle contained by segments of the other - i.e. XP ·XP " = XQ·XQ" in Figure 5. The point X can be inside or outside the circle. P' P X Q' Q S P' P Q' Q Fig. 7 Fig. 8 2 X Proof: In Figure 7, triangles P Q" X and QP " X are similar, because their angles at X are opposites, the angles at P and Q are equal because they are based on the same arc P " Q" (see 3 above), and the angles at P " and Q" are equal because they are based on the same arc P Q. This tells us that XQ" XP = and so XP · XP " = XQ · XQ" XQ XP " as required. In Figure 8, the angle as P " and Q" are equal, being based on the same arc P Q, and the angles at X are equal, so that the triangles XQP " and XP Q" are similar. Therefore, XQ XP " = and so XP · XP " = XQ · XQ" . " XQ XP The converse is also true, i.e. if XP · XP " = XQ · XQ" , then P, P " , Q, Q" are points on the circumference of a circle. For suppose XP · XP " = XQ · XQ" with X outside the circle, but Q, Q" , P, P " do not lie on a circle as in Figure 9. Y P' P Q' Q X Fig. 9 Since any three non-collinear points determine a circle, let the circle determined by P, Q and Q" intersect the line P X in the point Y , with Y "= P " . Then from above, XQ · XQ" = XP · XY . This forces P " to equal Y . 6. If, from a point outside a circle, a secant and a tangent are drawn, the rectangle contained by the whole secant and the part outside the circle will be equal to the square on the tangent, and conversely — thus XP · XP " = XT 2 in Figure 6. This is because the tangent XT is the limiting position of the secant XQQ" , and so XQ = XQ" = XT . 3 A P P' X Q B X Q' C T P' Fig. 5 Fig. 4 P Fig. 6 7. The angle subtended at the circumference of a circle by an arc AB is equal to the angle between the tangent at A and the chord AB. Thus in Figure 4, the angle ACB is equal to the angle between AB and the tangent at the point A. In Figure 4, we wish to show that ! C = the angle between chord AB and the tangent at A. Joining A and B to the centre O of the circle, we obtain an isosceles !AOB. The angle AOB is, say, α, which = 2 · ! C by 3 above, so that ! C = 12 α. Since the sum of the three angles of !AOB is π, angles ABO and BAO are both 12 (π − α). A T O C B Since the tangent T is perpendicular to the radius AO, ! T AO = π2 , and so ! T AB = ! T AO − ! BAO = π − 1 (π − α) = 1 α which equals ! C, and so the angle between 2 2 2 the tangent T A and the chord AB is equal to the angle inscribed in the arc AB as required. 4