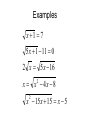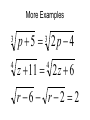Download Section 9.5 and 9.6

Section 8.5 and 8.6
Multiplying and Dividing
Radicals/Solving Radical
Equations
Multiplying Radicals
Multiplying radicals utilizes the previouslydiscussed concepts:
• The distributive property
• The FOIL method
• Simplifying radicals
• Combining like radical terms
The Rules
a  b  ab
a b  c d  ac bd
a a a
 a
2
a
a b  a b
Be Careful!!!
• Do not confuse the rules for multiplication
with the rules for addition.
Examples

2 32  9

 7  14  7  14 
 13  7  3  11
 6  2
4 p  7  p  9
 6 y  4 6 y  4
2
Dividing Radicals
• Dividing radicals is actually not division.
• Rationalizing the denominator is the
process of removing radicals from the
denominator.
• There are two cases for rationalizing the
denominator.
Case 1: One term in the
denominator
• Multiply numerator and denominator by
the term in the denominator.
12
6
5
24
52
y
242t 9
u 11
Case 2: Two terms in the
denominator
• Multiply numerator and denominator by
the conjugate of the denominator.
4
5 6
5 6
3 2
a b
a b
Solving Radical Equations
1. Isolate the radical expression, if possible.
2. Raise each side of the equation to a
power equal to the index.
3. Solve the resulting equation:
a. If linear, isolate the variable
b. If quadratic, solve by factoring
4. If you have more than one solution,
sometimes one of them won’t work. You
might want to check them.
Examples
x 1  7
5 x  1  11  0
2 x  5 x  16
x  x  4x  8
2
x  15 x  15  x  5
2
More Examples
3
p 5  2p 4
4
z  11  2 z  6
3
4
r 6  r 2  2