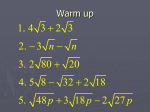Download 6_2MultiplyingandDividingRadicals

6.2 Multiplying and Dividing Radical Expressions
I. Multiplying Radical Expressions
Property: If n√a and n√b are real numbers, then n√a (n√b) = n√ab
Example 1: Multiplying Radicals (Simplify if Possible)
1a) √2 (√8) = √ 2 * 8 = √16 = 4
1b) ³√-5(³√25) = ³√-5 * ³√25 = ³√-125 = -5
1c) √-2 (√8) = the property for multiplying radicals does not apply. √-2 is not a real number.
1d) √3(√12)
1e) ³√3(³√-9)
1f) 4√4(4√-4)
Example 2: Simplifying Radical Expressions
 Assume that all variables are positive. Then absolute value symbols are never needed in
the simplified expressions.
2a) √72x³
Step 1: Factor into perfect square (or to nth index)
√72x³ = √6² * 2 * x² * x
Step 2: ^n√a (^n√b) = ^n√ab
√72x³ = √6² * x² (√2 * x)
Step 3: Simplify
6x√2x
2b) ³√80n5
2c) √50x4
2d) ³√x³ (Assume that x is positive for both ex.’s)
Example 3: Multiplying Radical Expressions
Multiply and Simplify ³√54x²y³ ( ³√5x³y4). Assume that all variables are positive.
Step 1: Multiply all coefficients and variable w/ exponents.
³√54x²y³ * 5x³y4 = ³√270x5y7
Step 2: Factor it down by factor by Prime Factor Tree or Perfect Cubes
3b) 3√7x³ * 2√21x³y²
3c) ³√25xy8* ³√5x4 y³
II. Dividing Radical Expression
 If n√a and n√b are real numbers and b ≠ 0, then n√a/n√b = n√a/b
Example 4: Dividing Radicals
Divide and Simplify. Assume that all variables are positive.
4a) ³√32/³√-4 = ³√-8 = -2
4b) Please remember when dividing exponents, you are subtracting them!
³√162x5
³√3x²
= √54x³ (simplify it down and get your answer)
4c) 4√1025x15
4
√4x
Rationalize the Denominator: In an expression, rewrite it so there are no radicals in any
denominators and no denominators in any radical; rationalizing the denominator of numerical
expression makes it easier to calculate its decimal approximation.
Example 5: Rationalize the denominator of each expression.
*Assume that all variables are positive.
5a) √2/√3
Step 1: Multiply the numerator and denominator by √3 (which is the denominator). The
denominator will become a whole number.
√2 (√3)
√6
√3 (√3) = 3
5b) √x³
√5xy
Cubic Root or Higher:
 If the denominator is not a perfect cube or nth root of the number, you must rewrite it into
one.
 Whatever was used to convert into a perfect cube or nth root must be multiplied to the
numerator as well.
5c) ³√2
³√4
3x
³√6x