Download Biostatistics Quantitative Data • Descriptive Statistics • Statistical

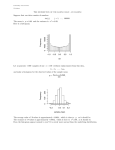
Biostatistics
Quantitative Data
Quantitative Data
This course will focus on the analysis of quantitative data which is
encountered in many areas of experimental research. Data may roughly
be grouped into 3 groups :
• Quantitative data : sperm concentration (mill/ml), height in cm, level
of hormones (measured on a continuous scale).
• Qualitative data : sex, race, work, groupings of quantitative data
(high/medium/low).
• Survival data : length of waiting time for some event. For some
individuals, however, the event is never recorded. These individuals are
censored and this makes some particular methods necessary.
• Descriptive Statistics
• Statistical Models
• One-sample and Two-Sample Tests
• Introduction to SAS-ANALYST
• T- and Rank-Tests using ANALYST
Thomas Scheike
We will concentrate on quantitative data and describe :
• Descriptive techniques. (Histograms, scatter-plots, means, standard
deviation, quantiles, percentiles, ...)
• Non-parametric methods. These are based on ranks of data, and may
be used for one-sample tests, two-sample tests (paired and un-paired),
one-sided analysis of variance and computation of measures of association
(Spearman correlation).
• Regression analysis techniques for normally distributed residuals.
These techniques include : t-test (paired and un-paired such), analysis
of variance (one- and two-sided), regression analysis, multiple regression
analysis, analysis of covariance)
We do, however, not discuss how to deal with repeated measures
where subjects are followed and measured repeatedly. When repeated
measures are encountered they may often be reduced to just one summary
number for each subject and thereby analysed by techniques dealt with
in this course.
1
2
Descriptive Statistics
We consider data on sperm concentration (mill/ml) on two groups
of people in a study. One group are members of an association that
promotes the development of organic agriculture (n=55), and another
group of workers are from a major Scandinavian airline carrier (n=141).
How these data were collected is very important if we want to conclude
more generally from the data. The data for both groups must be representative for the members of organic agriculture associations
and airline workers. This must be very carefully validated, but for
now we believe that this is the case.
The Histogram
The histogram is a different and better summary, it describes the distribution of the sperm concentrations for the two groups :
Airline
40
Frequency
0
Drawing the data is the most important part of the statistical analysis :
0
5
20
10
Frequency
15
60
20
80
Organic farmers
0
100
200
300
400
0
100
200
300
400
sas
400
eco
200
100
height × width = Frequency in group
if bars all have the same width this is not important. A difficulty is to
decide the width of the bars. Here are two different histograms:
0
Histogram
of
conc
Histogram
conc
0.0 4
0.0 3
0
100
200
300
400
0
conc
3
of
2.0
Density
1.8
0.0 2
1.6
Group
0.0 1
1.4
0.0 0
1.2
Density
1.0
0.0 0 0.0 2 0.0 4 0.0 6 0.0 8 0.010 0.012
sperm concentration
300
A histogram shows how the data is distributed, i.e., we can find out
how many men that have a sperm count lower that 100 mill/ml, say.
For the Airline people this is 110 (141) men and the organic farmers
have 35 (55) under 100 mill/ml. It is made by grouping of the sperm
concentrations and then deciding the height of each bar such that:
100
200
conc
4
300
400
The Histogram
The histogram describes the variability of the data. And we can
approximate the chance that a data-point is below some limit, above
some limit or between two limits by calculating the area of the histogram
in the appropriate area :
Percentiles
Frequency
60
80
Histogram of conc
40
Area is = chance (Frequency / number )
0
0.008
20
Histogram of conc
0
100
200
300
400
0.006
conc
0.000
0.002
0.004
Density
To describe the histogram we may find the data value for which 50 %
of the data is above or equal to and 50 % is below or equal to, this is the
median. After ordering the data in size the median is the value in the
middle of the data, for an even number of data points the median is the
average of the two middle values :
0
100
200
300
1 4 6 8 9 ∼ median = 6
400
conc
What is the probability of seeing a sperm concentration less than 40,
say, from a randomly chosen man among our men in the study.
1 4 6 7 8 9 ∼ median = (6 + 7)/2 = 6.5
Similarly the 25% percentile (quantile) is the data point for which at
least 25% of the data points have a lower or equal value and at least 75
% have a higher or equal value :
1 4 6 8 9 ∼ 25%percentile = 4
1 4 6 7 8 9 ∼ 25%percentile = 4
Find an approximate median in the histogram ?
5
6
Simple Summary Statistics
We can calculate the mean (average) and standard-deviation for the
two groups :
n
1 X
xi ,
x̄ =
n i=1
n
1 X
Variance =
(xi − x̄)2,
n − 1 i=1
and
v
u
u
n
1 X
u
SD = t
(xi − x̄)2
n − 1 i=1
The mean describes the midpoint of the data, and the standard deviation the spread of the data. These number may always be calculated.
Symmetric distributions are well characterized by these numbers, whereas
a skewed distribution will not be well described.
The Histogram
The histogram based on the data is an approximation of the population the data is a representative sample from. A particularly nice
histogram curve is the normal distribution :
0.2
0.1
normal density
0.3
0.4
Normal Distribution
0.0
0.4
Normal Distribution
−2
0
2
4
7
of
conc
Histogram
of
conc^0.3
0.4
Histogram
0.3
0.2
Density
0.1
0.0
If a distribution does not appear symmetric one should instead compute
median and various percentiles (25 % and 75 %, say) or give the range
of the data (largest and smallest value). For the Sperm data the spermconcentration was 77 (77) (mean (SD)), the median and range was 56 and
[0,402], respectively. What numbers are best suited to describe how the
sperm concentration varies ??
80
4
60
2
x
Frequency
0
40
−2
20
0.0
−4
which is a good approximation to many symmetric histograms. Some
properties of the normal curve is :
• The normal curve is symmetric around its mean.
• It is completely described by its mean and SD.
By saying that data is normally distributed we mean that the histogram
of the data is close (well approximated) to the normal curve. Sometimes
a transformation of the data is necessary to make this true
0
0.2
x
0.1
normal density
0.3
−4
0
100
200
300
400
0
conc
1
2
3
4
conc^0.3
8
5
6
Histogram of height
0.006
0.000
0.2
0.002
0.4
0.004
pnorm(x)
0.6
Density
0.008
0.8
0.010
1.0
There are tables of the standard normal distribution which has mean=0
and SD=1, and the area between two values for any other normal curve
can be found using this table by converting values to standard scores.
Example :
The height of Danish women are approximately normal with mean 165cm
and standard deviation 30cm. If a woman is chosen at random what is
the chance that she is lower than 180 cm.
Standard score = (180-165)/30 = 0.5, i.e., 180 is 0.5 standard deviations
above the mean. The chance of being less than 0.5 in a standard normal
is 0.65
Is it a reasonable statistical model ??
What is the chance of a randomly chosen woman is between 190 and 175?
Convert to standard scores = 0.83, 0.33
0.012
The Normal Distribution
Similarly, to how we use the histogram, based on the normal curve we
can work out how the data is distributed. The normal curve satisfies that
:
• 50 % of the area is under the mean.
• 95 % of the area is between [mean - 1.96 SD, mean + 1.96 SD].
• 68 % of the area is between [mean - 1 SD, mean + 1 SD].
• 2.5 % of the area is between [−∞, mean − 1.96SD].
150
0.0
100
200
250
height
−4
−2
0
2
4
x
The figure gives the cumulative distribution, i.e., what percent of the
distribution is below a given value.
The statement may formally be written as : P (X < 0.83) =
0.80; P (X < 0.33) = 0.63and P (0.33 < X < 0.83) = P (X <
0.83) − P (X < 0.33) = 0.80 − 0.63
This is based on the following precise statement about standard scores.
With Z normal with mean µ and variance σ 2 it follows that (Z − µ)/σ
is standard normal.
9
10
Distributions
We often draw histogram curves to show how the data is distributed
(is varying). How does these two histograms differ from the normal curve
:
Example:
Suppose that the sperm-concentration in the Danish population is right
skewed :
Standard Log Normal Distribution
Normal
Distribution
meanlog=3,sdlog=1
0.4
0.5
0.6
0.0 0 0.0 5 0.010 0.015 0.020 0.025 0.030
Log
100
200
300
400
0.2
0.3
0
0.0
0.1
If we draw 50 men at random from this distribution we get the following
numbers :
2
4
6
8
10
Histogram
for
sample
of
50
10
5
The first distribution is right skewed. i.e. data from this distribution
contains some very high values.
Frequency
15
20
0
0
Multi−Modal
Histogram of
Distribution
c(x1, x2)
50
100
150
0
20
40
60
Frequency
80
100
120
140
0
2
4
6
8
10
12
calculations give mean=27, SD=29, median=17, range=2,250
Now, drawing again gives that :
calculations give mean=34, SD=27, median=21, range=4,153
and again :
calculations give mean=53 , SD=115 , median= 16, range=2,287
and again :
calculations give mean=26 , SD=31 , median=20 , range=2,258
c(x1, x2)
This other curve have several modes (multi-modal).
11
12
Example cont’d :
Looking at concentrations on log-scale the population is distributed as
follows :
Distribution
mean=3,sd=1
0.4
Normal
Descriptive Statistics : Summary
• The histogram shows how the data is distributed, i.e., how it is
varying.
0.2
• The normal distribution is a histogram curve that is a good approximation to many histograms.
0.0
0.1
dnorm(3 + x, 3, 1)
0.3
• The area of the histogram represents frequency.
0
2
4
3
+
6
x
Drawing 50 men randomly from the population gives the following
histogram :
calculations give mean=2.9 , SD=0.99 , median=2.8 ,
Histogram
for
log
of
sample
of
50
6
8
10
• The median and range are useful summaries of how data are distributed. They should be calculated when the data are not (approximately) normally distributed.
0
2
4
Frequency
• The mean and standard deviation are useful summaries of how data
are distributed. They should be calculated only when the data are
approximately normally distributed.
1
2
3
4
5
range=[0.8,5.5]
Now, drawing another random sample of 50 gives :
mean=3.0 , SD=0.85 , median=3.0 , range=[1.3,5.0]
and again :
mean=2.9 , SD=1.00 , median=2.9 , range=[0.4,5.6]
and again :
mean=3.1 , SD=1.07 , median=3.1 , range=[0.7,4.9]
We conclude that for the right skewed data the mean and SD are highly
variable, for the normal data the mean and SD, however, provides a very
effective summary. The median stays constant for both distributions.
14
Statistical Models
When a physical quantity is measured several times we will get different
results due to measurement error and biological variation. For example,
measuring the height of a subject may yield the following histogram :
Estimation in Statistical Models
In a statistical model one wishes to learn primarily about the parameters of the model. However, to understand what can be learned about
these one must also study the variability present.
In the statistical model
0.8
13
0.6
Yi = µ + ǫi i = 1, ..., 200
189
Individual measurement = overall mean + noise
If we let the individual measurements be called Yi (the observed data)
the overall mean µ (unknown), and the noise ǫ, we have that
Y i = µ + ǫi
This is a statistical model that describes how the observed measurements arises. The model claims that the individual observations varies
around a fixed value (µ), and that the variation is ǫ. A model contains
two parts: a systematic part which is of scientific interest and a random
variation part which is due to biological and measurement error variation.
To complete the specification of the model we also specify how the random variation ǫi varies. We do this by specifying its distribution. It is
assumed that ǫi ∼ N (0, σ 2), i.e., it is normal with mean 0 and variance
σ2.
15
ȳ = µ̂ = µ +
n
1 X
ǫi
n i=1
The last term is an average of independent noise terms N (0, σ 2) and
2
mathematical arguments give that it is distributed as N (0, σn ). So we
have described exactly what is known about µ in µ̂ through finding its
distribution (N (µ, σ 2/n)). One way to think about this is that we have a
description of how the sample average is varying if we repeat the sampling.
The variance of the average is n times smaller than the variance of the
individual noise terms.
Normal
densities
1.5
188
x
1.0
187
normal density
186
0.5
185
What we see is variation around the average height. The variation is
due to both measurement error and biological variation. Based on the
above histogram it appears reasonable to claim that the variation may be
described by a normal distribution. We may phrase this as a statistical
model :
where ǫi ∼ N (0, σ ) are independent noise terms. We want to know µ
and σ. We may estimate these quantities by the sample average and
standard deviation.
n
1 X
Yi
ȳ = µ̂ =
n i=1
and
v
u
u
n
1 X
u
(Yi − ȳ)2
SD = σ̂ = t
n − 1 i=1
Looking at ȳ and using the statistical model we get that
0.0
0.0
0.2
0.4
2
−4
−2
0
2
x
16
4
for
log
of
sample
of
and
Normal
Approximation
30
40
Histogram
20
200
0
40
10
Histogram
Sperm analysis, cont’d
Drawing the best guess at how the population is distributed against
the histogram :
Frequency
Sperm analysis
Scientific interest in level of sperm concentration in Danish population.
We have representative sample from population.
We wish to see if the level in Denmark is equal to what WHO considers
the minimum level (20 mill/ml). A sample of 200 Danish men look like
this :
2
3
4
5
6
2
3
4
5
6
The log-transformed data appears to be distributed as a normal distribution.
A statistical model is now proposed to describe how the population is
varying, containing a systematic part (µ) which is the average log(sperm
concentration) in the population and a random variation part ǫi, which is
independent normal random variation N (0, σ 2) :
Yi = µ + ǫi i = 1, ..., 200
We do not know µ and σ. We may estimate these quantities by the
sample average and standard deviation.
under
Null
and
Observed
0.5 * 20 * dnorm(x + 4, log(20), slx)
30
n
1 X
Yi = 3.9
n i=1
Distribution
and
0
10
ȳ = µ̂ =
We see that the histogram and the normal curve approximate each
other well. So the statistical model is validated. Which means that
we have a reasonable description of the level of random variation, and a
reasonable description of the systematic variation.
We wish to investigate if the data is consistent with the null-hypothesis
H0 : µ = log(20), if this is not so, we are left with the alternative HA :
µ 6= log(20). The meaning of ”consistent with the null-hypothesis” is
in statistical terms equivalent to checking if the data could arise when
the null-distribution is true. The null-hypothesis claims that the data is
distributed around log(20), and if we use the description of the variation
found above, the data should arise as a random sample from the left hand
curve :
20
1
40
0
10
20
Frequency
30
1
v
u
u
u
t
n
1 X
(Yi − ȳ)2 = 0.95
n − 1 i=1
This means that our best guess is that the population has mean 3.9 and
the level of random variation is described by a normal distribution with
standard deviation equal to 0.95
SD = σ̂ =
0
2
4
6
8
The right hand curve is the normal approximation to the data. Formally
we write
Yi = log(20) + ǫi i = 1, ..., 200 ǫ ∼ N (0, 0.952).
17
18
Sperm analysis, cont’d
The question now is : how well does this fit with the average we found
in our data at 3.9 ?
Sperm analysis, The t-test
To further summarize how the observed sample average compares to
the null-hypothesis we can calculate how many standard deviations it is
different from the null-hypothesis :
The sample average is distributed as N (µ, σ 2/n), so if H0 is true, the
sample average is varying around log(20) with a standard deviation at
√
√
σ/ n (which we estimate as σ/ n = 0.95/14 = 0.05). Thus our guess
at how the average is varying under the null is N(log(20),(0.05)2).
6
Distribution of Mean under Null (log(20)
T =
ȳ − log(20)
√
= −18
SD/ n
which is t-distributed with n − 1 = degrees of freedom (p < 0.0001). We
√
define SEM = SD/ n, the standard error of the mean. A t-distribution
is varying slightly more than a normal :
t−dist f=19 and Normal
t−dist f=9 and Normal
0.4
0.4
0.3
0.3
0.3
3
0.2
dnorm(x, 0, 1)
0.2
dnorm(x, 0, 1)
0.2
dnorm(x, 0, 1)
2
0
2
4
6
0.1
0.1
0.1
1
0
8
How well does this fit with the data ??
−4
−2
0
x
2
4
0.0
0.0
x + 4
0.0
dnorm(x + 4, log(20), slx/200^0.5)
4
0.4
5
t−dist f=199 and Normal
−4
−2
0
2
x
4
−4
−2
0
2
4
x
because we had only a variable guess on the SD of the population.
Note that the t-test is on the form
observed − expected
T =
standard errror of observed
We now calculate the chance of getting a test-statistic as extreme as
or more extreme than the observed one. The chance is computed under
the null H0 (the p-value). The smaller this chance is the more evidence
against the null.
If the p-value is less than 5% we reject the null (at a 5 % level).
19
20
Statistical Models
The random variation in a statistical model is described by a distribution. Often a normal distribution.
The random variation may consist of several components depending on
the context. Different sources may be :
• Measurement error.
Statistical Models, Summary
The recipe when doing statistical analysis :
• Scientific hypothesis is formulated.
•
• Make graphs of data, to get a feel for the data, and the variability.
• Statistical model is proposed and validated.
• Inter-individual variation.
– Systematic variation, contains parameters about which the scientific hypotheses is formulated.
• Intra-individual variation.
– Random variation described as normal N (0, σ 2).
• Variation over time.
• Inference about parameters may be drawn in statistical model.
The random variation is not the object of interest but we must anyway
specify a model for it that appears reasonable to correctly understand how
much that can be learned about the systematic part of the variation.
22
21
One-sample Comparison’s, the t-test
Consider the 55 ecological farmers and the 141 airline workers :
Airline
40
Frequency
20
0
5
0
0
100
200
300
400
0
100
200
eco
300
400
sas
We now wish to investigate if the sperm-level is equal to the level 40
mill/ml (found in the literature) for the group of ecological farmers.
A statistical model is
Yi = µ + ǫi i = 1, ..., 55
where ǫ ∼ N (0, σ 2) are independent noise terms. We know that the data
is approximately normal when considered on a log-scale :
log−ECO
Histogram
log−SAS
15
20
15
0
0
5
5
10
Frequency
10
Frequency
ȳ − log(40)
= 0.51/0.14 = 3.6
SEM
which should be looked up in t-distribution with 54 = 55 − 1 degrees of
√
freedom, where SEM=SD/ n. We get a p-value at 0.001. Thus, if the
null was true and we drew 55 men from the population we would get an
average as different or more than the observed average with a chance at
0.001.
We conclude that the sperm-level is significantly higher than 40 mill/ml
in population of ecological farmers. A 95 % confidence interval for
mean-values we can not reject by a 5 % test are :
√
√
(µ̂ − 1.96 · SD/ n, µ̂ + 1.96 · SD/ n)
(4.2 − 1.96 · 0.14, 4.2 + 1.96 · 0.14) = (3.9, 4.4)
This is the range of values for the mean of the sperm-concentration we
believe in.
25
Histogram
The t-test
The one-sample t-test for the hypothesis H0 : µ = log(40) versus
HA : µ 6= log(40).
The null claims that we see is a sample from a population that varies
symmetrically around log(40).
T-test for H0 is
T =
10
Frequency
15
60
20
80
Organic farmers
2
3
4
log(eco[eco
5
>
6
0
0])
1
2
3
log(sas[sas
4
>
5
6
0])
and therefore investigate the scientific hypothesis on this scale.
Estimate µ and σ by sample average and sample standard deviation
n
1 X
ȳ = µ̂ =
Yi = 4.2
n i=1
and
v
u
u
n
1 X
t
(Yi − ȳ)2 = 0.96
SD = σ̂ = u
n − 1 i=1
23
24
Two-sample Comparison’s, the t-test
Consider the 55 ecological farmers and the 141 airline workers on a
log-scale :
Histogram log−SAS
25
Histogram log−ECO
20
15
A Non-parametric One-sample Test, The signed-rank test
Non-parametric techniques avoids the assumption of normally distributed residuals, and instead ask questions about the median for the
population. Still looking at the ecological farmers. We now take a subset
of 10 men:
15
10
Frequency
10
We make a Wilcoxon one-sample test a signed rank test.
Subtracting 40 from each of the sperm levels we get
-18
3.5
-4
1
15 18
2 3.5
30
5
34
6
40
7
49
8
80
9
160
10
Ordering these after absolute size and assigning them ranks. We check
if the sum of the rank’s of the negative values are as big as the ranks of
the positive values, as it should be under symmetry. The ranks of the
negative numbers are 4.5. We look it up in statistical table. The p-value
is p > 0.01 and p < 0.02. Doing the test on all the data gives a p-value
at 0.001.
0
H0 : Distribution symmetric around 0
versus
HA : Distribution not symmetric. (skewed for example)
0
5
5
and wish to test if they vary symmetrically around 40 mill/ml. We do
not specify a detailed statistical model but want to test if
Frequency
22 36 55 58 70 74 80 89 120 200
2
3
4
5
6
0
log(eco[eco > 0])
1
2
3
4
5
6
log(sas[sas > 0])
One may want to know if these two groups really could be varying
around the same level, and that the differences we see is due to random
variation.
We start by proposing a statistical model in which we can answer the
question:
Yi,j = µi + ǫi,j i = 1, 2, j = 1, ...ni
where ǫi,j ∼ N (0, σi2) are independent noise terms. The histograms of the
data shows that the model is a good description of the data on log-scale.
Estimating the mean and variability in the two populations underlying
the samples give that
µ1 = 3.9
µ2 = 4.2
σ12 = 1.08
σ22 = 0.90
One may use a normal approximation
to compute the p-value, i.e.,
r
compute µ = n(n + 1)/4 and σ = n(n + 1)(2n + 1)/24, and
T −µ
σ
for n > 20. For smaller values of n use a table.
Z=
25
26
Two-sample Comparison’s, the t-test
To carry out a two-sample t-test we first need to check if the variability
is the same in the two groups. We test if H0 : σ1 = σ2 versus HA : σ1 6=
σ2. And use the following test-statistic :
Non-parametric Two-sample Comparison’s, The rank test
The non-parametric rank test is also called the Wilcoxon-Mann-Whitney
test.
Consider two groups of data as before. We now wish to test if the distribution of the two population could be equal, or if this must be rejected
by a test.
The statistical model :
• : Yi,j ∼ arbitrary distribution Fi (·).
• : All data points are independent.
max(σ12, σ22)
min(σ12, σ22)
1.08
=
= 1.27
0.90
F =
which we should look up in F − distribution with (140, 54) degrees of
freedom (p=0.32). So we accept hypothesis. Now we can calculate a
combined estimate of the variability
(n1 − 1)σ12 + (n2 − 1)σ22
(n1 − 1) + (n2 − 1)
54 · 0.902 + 140 · 1.082
=
= 1.02
55 − 1 + 141 − 1
SD 2 =
With the combined variability estimate SD we can proceed to the twosample T-test for H0 : µ1 = µ2 versus HA : µ1 6= µ2
T =
y¯1 − y¯2
= 2.82
SD (1/n1) + (1/n2)
r
which we look up in t-distribution with n1 + n2 − 2 = f1 + f2 degrees of
freedom. (p=0.006).
• We conclude that the ecological farmers have a significantly
higher sperm-level than the airline workers.
A 95 % confidence interval for the difference in means of the two groups
are given by :
(y¯1 − y¯2 − 1.96 · SED, y¯1 − y¯2 + 1.96 · SED) = (0.3 − 2 · 0.1, 0.3 + 2 · 0.1)
r
where SED = SD ∗ ( (1/n1) + (1/n2)).
27
In this non-parametric model we wish to test if :
H0 : Distributions are the same
versus
HA : Distributions are not the same.
We calculate a test-statistic as follows:
• Pool all data and assign ranks.
• Sum ranks of smallest group.
• Look sum of ranks up in statistical table to get p-value.
Sum of ranks, T, for ecological farmers is 6342 (total sum of ranks
is 19306, and 19306 * (55/196) = 5405) which result in p-value at 0.0096
(computer program).
One may use a normal approximation to compute
the p-value, i.e.,
r
compute µ = n1(n1 + n2 + 1)/2 (5390) and σ = n2µ/6 (356), and
T −µ
σ
for n1, n2 > 10. For smaller values, use a table.
Z=
28
Paired Comparison’s
When data is paired the two measurements often are not independent:
• Measuring right- and left bicep.
• Growth before and after treatment.
• Height of men of women when sampled as couples.
With only two correlated measurements, the data may anyway be analysed by simple techniques.
A correct analysis is obtained by making one-sample analysis on the
differences. The differences between the before and after measurements
are namely independent among subjects. Therefore one should simply
test if the differences are varying around 0, by either a t-test or a signedrank-test.
When investigating the effect of some drug that prevents sun-burn, say,
we could apply the sun-lotion to one arm and placebo to the other. The
difference between the arms may be ascribed to the lotion. The difference
is a measure that is corrected for inter-individual variation, which may be
large.
Summary
• Make graphs of data.
One-sample test:
• When the variation is approximately normal the t-test may be used
to test a hypothesis about the mean of the underlying population. The
p-value provided is only valid if the variation is approximately normal.
A nice summary of data is provided by the confidence interval of the mean.
• When data is not normally distributed and interest is concentrated
on inference rather than estimates the signed-rank-test may be used. This
test is always valid. No confidence intervals may be given. Right skewed
data may be transformed to approximate normality by transformations
√
like x, x1/3, log.
Two-sample test:
• Two groups of data may be compared by the t-test when the variation is approximately normal and the variance of the residual variation
is equal in the two groups. A nice summary of difference between the
groups are given by the confidence interval for the difference between the
means.
• When data is not normally distributed and interest is concentrated
on inference rather than estimates the rank-test may be used. This test
is always valid. No confidence intervals may be given.
• Paired data is handled by sample techniques on the differences between the pairs.
29
30
Statistical Analysis using Analyst (SAS)
Analyst is a windows based application in the SAS statistical software.
SAS is activated by clicking :
start → statistik → SAS
in the lower lefthand corner. Analyst is activated after
solutions → analysis → Analyst
Commands will be presented as we need them for the various analyses,
and remember that the focus is on the statistical analyses rather than how
one do this and that.
We consider data on sperm concentration (mill/ml) on two groups
of people in a study. One group are members of an association that
promotes the development of organic agriculture (n=55), and another
group of workers from a major Scandinavian airline carrier (n=141).
now type a new name e.g. oeko12 if you are in from of machine
12.
The data-set contains the following variables :
obs observation number.
abstime length of abstinence in days.
age age of subject.
s1e2 group indicator.
conc sperm concentration (mill/ml).
volume volume of sperm sample (ml).
The data is loaded
file → open...
from n:\human\oeko that is a SAS data-set. Doing this the data will
appear in the data table. It consists of a record for each subject with the
variables described above.
To make your own new variables when you work with the data you
must create your own version of the data. You do this by saving your own
version of the data under a new name :
File → Save... →
31
32
Data Manipulations
A little bit of data manipulation is needed. New transformed variables
are constructed by setting the data frame in edit mode
edit → mode → edit
and then
data → transform → compute...
now type new variable name (e.g. conc3) and an expression
that defines the new variable in the box below the equality-sign (e.g.
conc**.3333). Now, a new variable called conc3 that is equal to
concentrations on cube-root–scale is defined and appears in the data
table.
√
Data Manipulations
To group a continuous variable according to its value and to define a
classification variable based on it :
data → transform → recode ranges...
in the recode dialog give column name (volume) and name of the new
grouped version (gvol) and click ok. Now in the next window give the
bounds 0,3; 3,4, and 4,15 for the first three groups and name them (1,2,3)
in the rightmost column, click ok.
To delete variable highlite the column in the data-table :
edit → delete
Alternatively, one may take on of the standard transformations like
conc after highlighting the column one wishes to transform by
data → transform → √
To make a variable that can be used for the one-sample test (e.g.
ld40=lconc-log(40))
data → transform → compute...
now type new variable name (ld40) and the expression that defines
the new variable in the box below the equality sign log(conc)-log(40).
To construct a subset of the data, e.g., the subset of ecological farmers
for an specific analysis for this group :
data → filter → subset data...
in the subset dialog you can apply a Where clause to the data (click
s1e2 and eq and constant value followed by 1 to select s1e2=1
the Airline workers).
33
34
Histograms
To make a histogram of concentration ( conc )
graphs → histogram...
select conc as the analysis variable and s1e2 as the class variable (the
classification variable). If the class variable is omitted no-classification
variable will used. Now, clicking ok does the job.
Simple descriptive Statistics
To compute mean, standard deviations, variances, medians and percentiles as well as the range
statistics → descriptive → distributions...
select conc as the analysis variable and s1e2 as the class variable (the
classification variable). Now, clicking ok does the job.
Output
Airline
80
Organic farmers
40
Frequency
0
0
5
20
10
Frequency
15
60
20
----------------------------- S1E2=1 -----------------------------Univariate Procedure
Variable=CONC
Moments
N
141 Sum Wgts
141
Mean
69.16461 Sum
9752.21
Std Dev
70.17659 Variance
4924.753
Skewness
2.172157 Kurtosis
5.780222
USS
1363973 CSS
689465.5
CV
101.4631 Std Mean
5.909935
T:Mean=0
11.70311 Pr>|T|
0.0001
Num ^= 0
139 Num > 0
139
M(Sign)
69.5 Pr>=|M|
0.0001
Sgn Rank
4865 Pr>=|S|
0.0001
0
100
200
300
400
0
eco
100
200
300
400
Quantiles(Def=5)
sas
To examine the normality of a variable one may draw the histogram
for a normal distribution on the same plot. To do this click fit in the
distribution-dialog and and select normal and ok in the fit-dialog before
clicking ok on the distribution-dialog.
100%
75%
50%
25%
0%
Range
Q3-Q1
Mode
Max
Q3
Med
Q1
Min
402
91
48
23
0
99%
95%
90%
10%
5%
1%
358
209
158
12
3.3
0
402
68
12
Extremes
Lowest
Obs
Highest
Obs
0(
40)
233(
92)
0(
1)
284(
102)
0.75(
67)
308(
32)
1.88(
60)
358(
104)
2.3(
132)
402(
69)
----------------------------- S1E2=2 -----------------------------Univariate Procedure
35
36
Variable=CONC
Moments
55 Sum Wgts
99.04727 Sum
86.39382 Variance
1.339362 Kurtosis
942620.1 CSS
87.22483 Std Mean
8.502394 Pr>|T|
54 Num > 0
27 Pr>=|M|
742.5 Pr>=|S|
N
Mean
Std Dev
Skewness
USS
CV
T:Mean=0
Num ^= 0
M(Sign)
Sgn Rank
55
5447.6
7463.891
1.118476
403050.1
11.64934
0.0001
54
0.0001
0.0001
----------------------------- S1E2=1 -----------------------------Univariate Procedure
Variable=DL40
Moments
Quantiles(Def=5)
100%
75%
50%
25%
0%
Max
Q3
Med
Q1
Min
354
138
69
33
0
Range
Q3-Q1
Mode
One-sample T-test and Signed Rank Test
We wish to examine if the hypothesis that the sperm level varies around
40 mill/ml can be statistically rejected or validated. To make a one-sample
t-test first transform to log-scale to obtain approximate normality and
then compute a new variable dl40=lconc-log(40) (see above). Now,
statistics → descriptive → distributions...
selecting the variable dl40 and with class equal to s1e2 does the job.
Output:
99%
95%
90%
10%
5%
1%
354
297
259
15
9.1
0
354
105
69
N
Mean
Std Dev
Skewness
USS
CV
T:Mean=0
Num ^= 0
M(Sign)
Sgn Rank
139
0.091883
1.080798
-0.79219
162.3748
1176.271
1.002305
139
9.5
816
Sum Wgts
Sum
Variance
Kurtosis
CSS
Std Mean
Pr>|T|
Num > 0
Pr>=|M|
Pr>=|S|
139
12.7718
1.168125
1.421361
161.2013
0.091672
0.3180
79
0.1265
0.0862
Extremes
Quantiles(Def=5)
Lowest
0(
5.5(
9.1(
11(
14(
Obs
40)
15)
35)
42)
10)
Highest
264(
264(
297(
322(
354(
Obs
32)
33)
47)
14)
51)
100%
75%
50%
25%
0%
Max
Q3
Med
Q1
Min
Range
Q3-Q1
Mode
2.307573
0.832909
0.182322
-0.51083
-3.97656
99%
95%
90%
10%
5%
1%
2.191654
1.704748
1.373716
-1.20397
-1.63476
-3.05761
6.284134
1.343735
-1.20397
Extremes
Lowest
-3.97656(
-3.05761(
-2.85597(
-2.69563(
-2.56395(
Obs
67)
60)
132)
111)
49)
Highest
1.762159(
1.960095(
2.04122(
2.191654(
2.307573(
37
Moments
54 Sum Wgts
0.541879 Sum
0.958596 Variance
-0.50364 Kurtosis
64.55813 CSS
176.9023 Std Mean
4.153971 Pr>|T|
54 Num > 0
14 Pr>=|M|
428.5 Pr>=|S|
54
29.26144
0.918905
-0.00368
48.70198
0.130448
0.0001
41
0.0002
0.0001
Quantiles(Def=5)
100%
75%
50%
25%
0%
Max
Q3
Med
Q1
Min
2.180417
1.238374
0.545227
0.09531
-1.98413
Range
Q3-Q1
Mode
99%
95%
90%
10%
5%
1%
2.180417
2.004853
1.867949
-0.85567
-1.29098
-1.98413
4.164549
1.143064
0.545227
Obs
Highest
15) 1.88707(
35) 1.88707(
42) 2.004853(
10) 2.085672(
29) 2.180417(
Missing Value
Count
% Count/Nobs
One-sample T-test
Alternatively one may use a special menu that has been designed especially for the one-sample t-test
statistics → hypothesis tests → One-sample t-test...
selecting the variable lconc and entering the mean we wish to test as 4.
Note that the t-test should be carried out only the group of ecological
farmers, say, and that the active data-set therefore should be only this
group. To make the test it is necessary to construct a new data set that
consists of the group of interest as done in the data manipulation section
above.
Output:
One Sample T Test for a Mean
Sample Statistics for LCONC
N
Mean
Std. Dev.
Std. Error
------------------------------------------------193
3.91
1.07
0.08
Hypothesis Test
Null hypothesis:
Alternative:
Mean of LCONC = 4
Mean of LCONC ^= 4
t Statistic
Df
Prob > t
---------------------------------1.217
192
0.2249
Extremes
Lowest
-1.98413(
-1.48061(
-1.29098(
-1.04982(
-0.98083(
92)
102)
32)
104)
69)
38
Missing Value
.
Count
2
% Count/Nobs
1.42
----------------------------- S1E2=2 -----------------------------Univariate Procedure
Variable=DL40
N
Mean
Std Dev
Skewness
USS
CV
T:Mean=0
Num ^= 0
M(Sign)
Sgn Rank
Obs
Obs
32)
33)
47)
14)
51)
To make the t-test of the two groups, you can specify that you want it done for
the two groups under the variables button, by given s1e2 as the by variable.
.
1
1.82
39
40
Two-sample T-test for Means (un-paired data)
To compare the concentrations for the two groups
statistics → hypothesis tests → Two-sample t-test for means...
selecting the variable lconc and the group variable s1e2.
Output:
Two Sample T Test for the Means of LCONC within S1E2
Sample Statistics
Group
N
Mean
Std. Dev.
Std. Error
-------------------------------------------------1
139
3.780763
1.0808
0.0917
2
54
4.230758
0.9586
0.1304
Two-sample T-test for Variances (un-paired data)
To compare the concentrations for the two groups
statistics → hypothesis tests → Two-sample t-test for variances...
selecting the variable lconc and the group variable s1e2. Output:
Two Sample Test for Variances of LCONC within S1E2
Sample Statistics
S1E2
Group
N
Mean
Std. Dev.
Variance
-------------------------------------------------1
139
3.7808
1.0808
1.1681
2
54
4.2308
0.9586
0.9189
Hypothesis Test
Hypothesis Test
Null hypothesis:
Alternative:
Null hypothesis:
Alternative:
Mean 1 - Mean 2 = 0
Mean 1 - Mean 2 ^= 0
If Variances Are
t statistic
Df
Pr > t
---------------------------------------------------Equal
-2.677
191
0.0081
Not Equal
-2.822
108.14
0.0057
Variance 1 / Variance 2 = 1
Variance 1 / Variance 2 ^= 1
- Degrees of Freedom F
Numer.
Denom.
Pr > F
---------------------------------------------1.27
138
53
0.3203
It is useful to supplement the analysis with some plots. Try for example the
plots button, and select one of the plots.
The conclusions are based on an assumption of equal variances, and this should
be validated. The output may indicate that this is the case, but if in doubt one
can carry out a test that shows have serious the deviation from equal variances
are.
41
42
Two-Sample Signed Rank Test
The two-sample signed rank test can more generally by considered as a special
case of the Kruskal-Wallis test that test if k groups have the same distribution.
To carry out the two-sample signed rank test :
statistics → ANOVA → non-parametric one-way ANOVA...
selecting the variable conc and the group variable s1e2.
Output:
Exercise-I
Rather than considering the concentration we shall now consider the volume of each sperm sample as the parameter of interest. We wish to compare the
ecological farmers and the airline workers.
A volume of 3 ml is considered normal. Investigate further if the two groups
are normal in this respect.
Wilcoxon Scores (Rank Sums) for Variable CONC
Classified by Variable S1E2
S1E2
1
2
N
141
55
Sum of
Scores
Expected
Under H0
Std Dev
Under H0
Mean
Score
12964.0 13888.5000 356.782425
91.943262
6342.0
5417.5000 356.782425 115.309091
Average Scores Were Used for Ties
3) Without doing any computer work make a strategy for how such an analyses
can and should be carried out. What descriptive plots and statistics are needed ?
What hypothesis are formulated and tested ? How will you validate the necessary
assumptions for the suggested analysis ?
4) Do the analyses, make the plots and so on. Remember to interpret the
results according to the subject matter.
Wilcoxon 2-Sample Test (Normal Approximation)
(with Continuity Correction of .5)
S =
6342.00 Z =
2.58981
Prob > |Z| = 0.0096
T-Test Approx. Significance = 0.0103
Kruskal-Wallis Test (Chi-Square Approximation)
CHISQ = 6.7144 DF = 1 Prob > CHISQ = 0.0096
43
44