Download Chapter 6 Probability

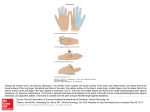
Chapter 5
5.3 Conditional Probability
and Independence
Warm up
1. Imagine that we shuffle a standard deck of cards
thoroughly and deal one card. Let’s define
events F: getting a face card and H: getting a
heart.
a. Make a two-way table that displays the sample
space.
b. Find P(F and H)
c. Make a Venn Diagram
d. Explain why P(F or H)  P(F) + P(H). Then use the
general addition rule to find P(F or H).
Face
Card
Not a Face
card
Total
Heart
3
10
13
Not a Heart
9
30
39
Total
12
40
52
b) P(F and H) = P(F ∩ H) = 3/52
H
F
9
3
10
30
d) P(F or H) = P(F) + P(H) is only if F and H are disjoint events but they have an
intersection so you need to subtract that out and not count it twice.
P(F or H) = P(F) + P(H) –P(F and H) = 12/52 + 13/52 – 3/52 = 22/52
2. Deborah and Matthew are anxiously awaiting word
on whether they have been made partners of the law
firm. Deborah guesses that her probability of making
partner is .7 and that Matthew’s is .5. This assignment
of probabilities does not give us enough information to
compute the probability that at least one of the two is
promoted. If Deborah also guesses that the probability
that both she and Matthew are made partners is .3,
a) P(D ∩ M) =
c) P(Dc ∩ M)=
.3
.2
b) P(D ∩ Mc)= .4
d) P(Dc ∩ Mc)= .1
Interpret the probability statement in words
3. Call a household prosperous if its income
exceeds $100,000. Call the household educated if
the householder completed college. Select an
American household at random, and let A be the
event that the selected household is prosperous
and B the event that it is educated. According to
the Census Bureau, P(A)=0.134, P(B)=0.254, and
the joint probability that a household is both
prosperous and educated is P(A and B)=0.080.
What is the probability P(A or B) that the
household selected is either prosperous or
educated?
P(A or B) = P(A) + P(B) – P(A and B)
P(A or B) = 0.134 + 0.254 – 0.080
= 0.308
What is Conditional Probability?
The probability we assign to an event can change if we know that some
other event has occurred. This idea is the key to many applications of
probability.
When we are trying to find the probability that one event will happen under
the condition that some other event is already known to have occurred, we
are trying to determine a conditional probability.
The probability that one event happens given that another
event is already known to have happened is called a
conditional probability.
Suppose we know that event A has happened. Then the
probability that event B happens given that event A has
happened is denoted by P(B | A).
Read | as “given
that” or “under the
condition that”
If we know that a randomly selected student has
pierced ears, what is the probability that the
student is male? P(is male given has pierced ears) =
19/103 or about 18.4%
If we know that a randomly selected student is
male, what’s the probability that the student
has pierced ears?
P(has pierced ears given is a male)
= 19/90 or about 21.1%
Pierced ears
Male
71
71/178
19
19/178
84
84/178
4
4/178
19
19
178
P 𝑚𝑎𝑙𝑒 𝑝𝑖𝑒𝑟𝑐𝑒𝑑 𝑒𝑎𝑟𝑠 =
=
103
103
178
Calculating Conditional
Probabilities
Calculating Conditional Probabilities
To find the conditional probability P(A | B), use the formula
P(A | B) =
P(A Ç B)
P(B)
The conditional probability P(B | A) is given by
P(B | A) =
P(B Ç A)
P(A)
Who Reads the Newspaper?
In an apartment complex, 40% of residents read USA today. Only 25% read the New York Times.
5% of residents read both papers. The Venn Diagram below describes the residents.
What is the probability that a randomly selected resident who reads USA Today also reads the
New York Times?
P(A  B)
P(B | A) 
P(A)


P(A  B)  0.05
P(A)  0.40
0.05
P(B | A) 
 0.125
0.40
There is a 12.5% chance that a randomly selected resident who reads
USA Today also reads the New York Times.
Going back to yesterday’s example, what is the
probability that a randomly selected household with a
landline also has a cell phone?
Landline
No
landline
Total
Cell
phone
0.51
No cell
phone
0.09
0.38
0.02
0.40
0.89
0.11
1.00
Total
0.60
𝑃(𝑐𝑒𝑙𝑙 𝑝ℎ𝑜𝑛𝑒 𝑎𝑛𝑑 𝑙𝑎𝑛𝑑𝑙𝑖𝑛𝑒)
P 𝑐𝑒𝑙𝑙 𝑝ℎ𝑜𝑛𝑒 𝑙𝑎𝑛𝑑𝑙𝑖𝑛𝑒 =
=
𝑃(𝑙𝑎𝑛𝑑𝑙𝑖𝑛𝑒)
0.51
= 0.85
0.60
Calculating Conditional Probabilities
Consider the two-way table on page 321. Define events
E: the grade comes from an EPS course, and
L: the grade is lower than a B.
Total
6300
1600
2100
Total 3392 2952
Find P(L)
P(L) = 3656 / 10000 = 0.3656
Find P(E | L)
P(E | L) = 800 / 3656 = 0.2188
Find P(L | E)
P(L| E) = 800 / 1600 = 0.5000
3656
10000
The General Multiplication Rule
General Multiplication Rule
The probability that events A and B both occur can be
found using the general multiplication rule
P(A ∩ B) = P(A) • P(B | A)
where P(B | A) is the conditional probability that event B
occurs given that event A has already occurred.
In words, this rule says that for both of two events to
occur, first one must occur, and then given that the first
event has occurred, the second must occur.
Playing in the NCAA
About 55% of high school students participate in a
school athletic team at some level, and about 5% of
these athletes go on to play on a college team in the
NCAA
(http://www.washingtonpost.com/wp-dyn/content/article/2009/09/23/AR2009092301947.html,
http://www.collegesportsscholarships.com/percentage-high-school-athletes-ncaa-college.htm).
Problem: What percent of high school students play a
sport in high school and go on to play a sport in the
NCAA?
We know P(high school sport) = 0.55 and P(NCAA sport |
high school sport) = 0.05, so P(high school sport and NCAA
sport) = P(high school sport) x P(NCAA sport | high school
sport) = (0.55)(0.05) = 0.0275. Almost 3% of high school
students will play a sport in high school and in the NCAA.
Tree Diagrams
The general multiplication rule is especially useful when a chance
process involves a sequence of outcomes. In such cases, we can use a
tree diagram to display the sample space.
Consider flipping a coin
twice.
What is the probability of
getting two heads?
Sample Space:
HH HT TH TT
So, P(two heads) = P(HH) = 1/4
Tree diagram
• A easy way to organize outcomes
• Helps to make sure that we don’t overlook any
outcomes
• Create a tree diagram for flipping a coin and
then rolling a die
P(A ∩ F)
P(A ∩ FC)
P(B ∩ F)
P(B ∩ FC)
P(C ∩ F)
P(C ∩ FC)
Example: Tree Diagrams
The Pew Internet and American Life Project finds that 93% of teenagers
(ages 12 to 17) use the Internet, and that 55% of online teens have
posted a profile on a social-networking site.
What percent of teens are online and have posted a profile?
P(online) = 0.93
P(profile | online) = 0.55
P(online and have profile) = P(online)× P(profile | online)
= (0.93)(0.55)
= 0.5115
51.15% of teens are online and have posted
a profile.
Shannon hits the snooze bar on her alarm clock on 60% of school
days. If she doesn’t hit the snooze bar, there is a 0.90 probability that
she makes it to class on time. However, if she hits the snooze bar,
there is only a 0.70 probability that she makes it to class on time.
0.4
0.6
0.9
On time
P(no Snooze and on time)=
0.4 * 0.9 = 0.36
0.1
Late
P(no Snooze and late)=
0.4 * 0.1 = 0.04
Doesn’t snooze
0.7
Hits snooze bar
0.3
On time
Late
P(Snooze and on time)=
0.6 * 0.7 = 0.42
P(Snooze and late)=
0.6 * 0.3 = 0.18
Total: 0.36 + 0.04 + 0.42 + 0.18 = 1
a) What is the probability that Shannon hits the
snooze bar and is late for class? P(Snooze and late)=
0.6 * 0.3 = 0.18
b) What is the probability that Shannon doesn’t
hit the snooze bar and is late? P(no Snooze and late)=
0.4 * 0.1 = 0.04
c) What is the probability that Shannon was late?
P(no Snooze and late)+P(Snooze and late) = 0.04 + 0.18 = 0.22
d) Suppose Shannon is late for school. What is
the probability that she hit the snooze button
𝑃(𝑠𝑛𝑜𝑜𝑧𝑒 𝑎𝑛𝑑 𝑙𝑎𝑡𝑒)
that morning?
𝑃 𝑠𝑛𝑜𝑜𝑧𝑒 𝑙𝑎𝑡𝑒 =
𝑃(𝑙𝑎𝑡𝑒)
0.18
𝑃 𝑠𝑛𝑜𝑜𝑧𝑒 𝑙𝑎𝑡𝑒 =
= 0.818
0.22
Example: Who Visits YouTube?
Video-sharing sites, led by YouTube , are popular destinations on the Internet. About 27% of
adult Internet users are 18-29 yrs old, another 45% are 30-49 yrs old, and the remaining
28% are 50 and over. The Pew Internet and American Life Project finds that 70% of Internet
users aged 18-29 have visited a video-sharing site, along with 51% of those aged 30-49 and
26% of those 50 and older. What percent of all adult Internet users visit video-sharing sites?
P(video yes ∩ 18 to 29) = 0.27 • 0.7
=0.1890
P(video yes ∩ 30 to 49) = 0.45 • 0.51
=0.2295
P(video yes ∩ 50 +) = 0.28 • 0.26
=0.0728
P(video yes) = 0.1890 + 0.2295 + 0.0728 = 0.4913
Media usage and good grades
The Kaiser Family Foundation recently released a study about
the influence of media in the lives of young people aged 8–18
(www.kff.org/entmedia/mh012010pkg.cfm). In the study, 17%
of the youth were classified as light media users, 62% were
classified as moderate media users, and 21% were classified as
heavy media users. Of the light users who responded, 74%
described their grades as good (A’s and B’s), while only 68% of
the moderate users and 52% of the heavy users described
their grades as good. Suppose that we selected one young
person at random.
(a) Draw a tree diagram to represent this situation.
(b) Find the probability that this person describes his or her
grades as good.
(c) Given that this person describes his or her grades as good,
what is the probability that he or she is a heavy user of media?
0.74
Good
0.26
Bad
0.68
Good
0.32
Bad
Light user
0.17
0.62
Moderate user
0.21
0.52
Heavy user
0.48
Good
Bad
(b) There are three groups of students who say they get good grades: those who are light users and get good
grades, those who are moderate users and get good grades, and those who are heavy users and get good grades.
Because these groups are mutually exclusive, we can add the probabilities of being in one of these three groups.
P(good grades) = (0.17)(0.74) + (0.62)(0.68) + (0.21)(0.52) = 0.1258 + 0.4216 + 0.1092 = 0.6566. About 66% of
the young people would describe their grades as good.
(c) Using the tree diagram,
P(heavy user | good grades) =
P(heavy user and good grades)
P(good grades)
0.1092
0.1092

 0.166
0.1258  0.4216  0.1092 0.6566
About 17% of young people who say they have good grades are heavy users of media.
False positives and drug testing
Many employers require prospective employees to
take a drug test. A positive result on this test
indicates that the prospective employee uses illegal
drugs. However, not all people who test positive
actually use drugs. Suppose that 4% of prospective
employees use drugs, the false positive rate is 5%,
and the false negative rate is 10%.
(http://www.cbsnews.com/stories/2010/06/01/heal
th/webmd/main6537635.shtml).
A randomly selected prospective employee tests
positive for drugs. What is the probability that he
actually took drugs?
0.04
0.96
0.9
positive
0.1
negative
Drugs
0.05
No drugs
0.95
positive
negative
We want to find P(took drugs | positive test) =
Two groups tested positive: those who take drugs and test
positive (probability = (0.04)(0.90) 0.036) and those who don’t
take drugs and test positive (probability = (0.96)(0.05) = 0.048),
so the probability of testing positive is 0.036 + 0.048 = 0.084.
0.036
0.036
Thus, P(took drugs | positive test) =

 0.429
0.036  0.048
0.084
That is, 42.9% of the prospective employees who test positive
actually took drugs.
Conditional Probability and Independence
When knowledge that one event has happened does not change the
likelihood that another event will happen, we say that the two events
are independent.
Two events A and B are independent if the occurrence of one
event does not change the probability that the other event will
happen. In other words, events A and B are independent if
P(A | B) = P(A) and P(B | A) = P(B).
When events A and B are independent, we can simplify the general
multiplication rule since P(B| A) = P(B).
Multiplication rule for independent events
If A and B are independent events, then the probability that A and
B both occur is
P(A ∩ B) = P(A) • P(B)
Multiplication Rule for Independent Events
Following the Space Shuttle Challenger disaster, it was determined that the
failure of O-ring joints in the shuttle’s booster rockets was to blame. Under
cold conditions, it was estimated that the probability that an individual O-ring
joint would function properly was 0.977.
Assuming O-ring joints succeed or fail independently, what is the
probability all six would function properly?
P( joint 1 OK and joint 2 OK and joint 3 OK and joint 4 OK and joint 5 OK
and joint 6 OK)
By the multiplication rule for independent events, this probability is:
P(joint 1 OK) · P(joint 2 OK) · P (joint 3 OK) • … · P (joint 6 OK)
= (0.977)(0.977)(0.977)(0.977)(0.977)(0.977) = 0.87
There’s an 87% chance that the shuttle would launch safely under similar
conditions (and a 13% chance that it wouldn’t).
Are the events “being a high school graduate” and
“being a homeowner” independent?
Homeowner
Not a homeowner
Total
High school
graduate
221
89
310
Not a high school
graduate
119
71
190
Total
340
160
500
To prove independence:
𝑃 𝐺 𝐻 =? 𝑃(𝐺)
221 310
≠
340 500
Since these two probabilities are not equal to each other,
then these events are not independent of each other.
Is there a relationship between gender and relative finger length? To find out, we
used the random sampler at the United States CensusAtSchool Web site
(www.amstat.org/censusatschool) to randomly select 452 U.S. high school students
who completed a survey. The two-way table shows the gender of each student and
which finger was longer on their left hand (index finger or ring finger).
Problem: Are the events “female” and “has a longer ring finger” independent? Justify
your answer.
Index finger
Ring finger
Same length
Total
Female
78
82
52
212
Male
45
152
43
240
Total
123
234
95
452
Solution: To check whether two events are independent, we need to check whether knowing a
student’s gender changes the probability that the student has a longer ring finger. If a student is
female, then the probability she has a longer ring finger is P(ring finger | female) = 82/212 =
0.387. However, the unconditional probability of having a longer ring finger is P(ring finger) =
234/452 = 0.518. These two probabilities are not equal, so the events “female” and “has a
longer ring finger” are not independent. Knowing that a student is female makes it less likely
that her ring finger is longer than her index finger.