* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 03 Starlight and Atoms
Rutherford backscattering spectrometry wikipedia , lookup
Electron configuration wikipedia , lookup
Bremsstrahlung wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Matter wave wikipedia , lookup
Atomic absorption spectroscopy wikipedia , lookup
Planck's law wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Electron scattering wikipedia , lookup
Photoelectric effect wikipedia , lookup
Wave–particle duality wikipedia , lookup
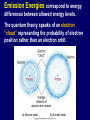
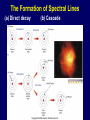
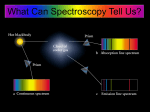
Starlight and Atoms Electromagnetic Radiation Waves Spectrum Black Body Radiation Atoms and Atomic Transitions Kirchoff’s Laws of Radiation The Amazing Power of Starlight Just by analyzing the light received from a star, astronomers can retrieve information about a star’s 1. Total energy output 2. Surface temperature 3. Radius 4. Chemical composition 5. Velocity relative to Earth 6. Rotation period Information from the Skies Electromagnetic Radiation: Transmission of energy through space using traveling waves of electric and magnetic fields Examples: •Radio •Infrared •Visible Light •Ultraviolet •X-rays •Gamma rays Waves Wave motion: transmits energy without the physical transport of material. Sound, water and light, for example, transmit energy with wave motion. Example: Water Waves ■ Water moves up and down locally ■ Wave travels and transmits energy Properties of Waves Frequency (f or n): number of wave crests that pass a given point per second Period (P): time between passage of successive crests Relationship: Frequency = 1 / Period f = ν = 1/P Wavelength (l): distance between successive crests Velocity (c): speed at which crests move Relationship: Velocity = Wavelength / Period c = l/P = ln = l f l Electromagnetic Waves: Oscillating electric and magnetic fields. Changing electric field creates a magnetic field, and vice versa. Speed of electromagnetic waves: c = 3.0 x 108 m/s The Wave Nature of Radiation Diffraction is purely a wave phenomenon. If light were made of particles, we would see a spot the size of the hole, with no fuzziness. Light as Particles • Light can also appear as particles, called photons (explains, e.g., photoelectric effect). • A photon has a specific energy E, proportional to the frequency n : E=hn=hf h = 6.626x10-34 J s is the Planck constant. The energy of a photon does not depend on the intensity of the light!!! The higher the intensity, the greater the number of photons The Electromagnetic Spectrum Wavelength Frequency Need satellites to observe High flying air planes or satellites Visible Spectrum Color and Temperature Stars appear in different colors, from blue (like Rigel) Orion Betelgeuse via green / yellow (white) (like our Sun) to red (like Betelgeuse). Rigel These colors tell us about the star’s temperature. Temperature Temperature is a measure of average internal kinetic energy The Kelvin Temperature Scale • All thermal motion ceases at 0K • Water freezes at 273 K and boils at 373 K Heat Transport Heat is transported by 3 physical mechanisms: • Conduction • Radiation • Convection Thermal Radiation The light from a star is usually concentrated in a rather narrow range of wavelengths. The spectrum of a star’s light is approximately a thermal spectrum called a black body spectrum. A perfect black body emitter would not reflect any radiation, thus the name “black body.” The mathematical formula was derived by Max Planck (1900) and is also called Planck radiation Laws of Thermal Radiation 1. The hotter an object is, the more luminous it is. Stefan’s Law: F = TK 4 (where F (flux) is power/unit area, σ = 5.67 x 10-8 W/m2·K4 , TK is the temperature in Kelvin). 2. The peak of the black body spectrum shifts towards shorter wavelengths when the temperature increases. Wien’s displacement law: l max ≈ 2,900,000 nm /TK Note how the hottest star looks blue and the coolest star looks red Light and Matter Spectra of stars are more complicated than pure black body spectra. They have characteristic lines, called absorption lines. To understand these lines, we need to understand atomic structure and the interactions between light and atoms. Different Kinds of Atoms • The kind of atom depends on the number of protons in the nucleus. • Most abundant: Hydrogen (H), with one proton (+ 1 electron). • Next: Helium (He), with 2 protons (and 2 neutrons + 2 el.). Helium 4 Different numbers of neutrons different isotopes Emission Energies correspond to energy differences between allowed energy levels. The quantum theory speaks of an electron “cloud” representing the probability of electron position rather than an electron orbit. Emission Lines of Hydrogen Most prominent lines in many astronomical objects: Balmer lines of hydrogen Atomic Transitions An electron can be kicked into a higher orbit when it absorbs a photon with exactly the right energy. The photon is absorbed, and the electron is in an excited state. Eph = E3 – E1 Eph = E4 – E1 Wrong energy (Remember that Eph = h n) • All other photons pass by the atom unabsorbed. The Formation of Spectral Lines (a) Direct decay Absorption (b) Cascade Emission Absorption Emission Spectral Lines Emission lines from single elements. When there are multiple elements, spectral lines of each element are superimposed in the spectrum and are used to identify all of the elements present. H Na He Ne Hg Absorption spectra and emission spectra can be used to identify elements. These are emission and absorption spectra of sodium: Kirchhoff’s Laws of Radiation 1. A solid, liquid, or dense gas excited by heat to emit light will radiate at all wavelengths and produce a continuous spectrum. Kirchhoff’s Laws of Radiation 2. If a continuous spectrum of light passes through a cool, low-density gas exciting its electrons to higher states, the result will be an absorption spectrum. Light excites electrons in atoms to higher energy states Spectral lines correspond to the transition energies that are absorbed from the continuous spectrum. Kirchhoff’s Laws of Radiation 3. A low-density gas excited to emit light will do so at specific wavelengths and thus produce an emission spectrum. Light excites electrons in atoms to higher energy states Electron transitions back to lower energy states emits light at specific frequencies The Spectra of Stars Inner, dense layers of a star produce a continuous (black body) spectrum. Cooler surface layers absorb light at specific frequencies. This implies that the spectra of stars are absorption spectra. Absorption Spectrum Dominated by Balmer Lines Modern spectra are usually recorded digitally and represented as plots of intensity vs. wavelength Emission nebula, dominated by the red Ha line.