* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download slides - Center for Collective Dynamics of Complex Systems (CoCo)
Pattern recognition wikipedia , lookup
Natural computing wikipedia , lookup
Theoretical computer science wikipedia , lookup
A New Kind of Science wikipedia , lookup
Computational complexity theory wikipedia , lookup
Turing machine wikipedia , lookup
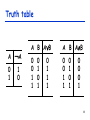
Turing's proof wikipedia , lookup
Algorithm characterizations wikipedia , lookup
History of the Church–Turing thesis wikipedia , lookup
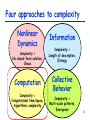
NECSI Summer School 2008 Week 3: Methods for the Study of Complex Systems Computation Theory BB10B Hiroki Sayama [email protected] Four approaches to complexity Nonlinear Dynamics Complexity = No closed-form solution, Chaos Computation Complexity = Computational time/space, Algorithmic complexity Information Complexity = Length of description, Entropy Collective Behavior Complexity = Multi-scale patterns, Emergence 2 Computation? A sequence of rewritings applied to a symbolic representation of something • Rewriting rules are predefined and fixed so that: – Process of computation is efficient – Final result is accurate and useful 3 Propositional Logic Proposition • A logical statement that is either true or false – “A human is an animal.” (true) – “An animal is a human.” (false) • These are both valid propositions 5 Propositional variables Propositional variables – “A human is an animal.” (true) → A – “An animal is a human.” (false) → B Truth value A = true (1), B = false (0) Propositional logic is about truth values only; no semantics involved 6 Logical operators • NOT (negation) ¬A, A • OR (disjunction) A∨B, A+B • AND (conjunction) A∧B, AB 7 Truth table A ¬A 0 1 1 0 A B A∨B A B A∧B 0 0 1 1 0 0 1 1 0 1 0 1 0 1 1 1 0 1 0 1 0 0 0 1 8 Logical formula • Symbolic expressions made of propositional variables and logical operators ¬B∧C (A∧B)∨(B∧¬C) – They are also propositions, and their truth values will be determined if truth values of all variables are given 9 Truth table of logical formula • X = (A∧B)∨(B∧¬C) A B C X 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 0 0 1 1 10 Exercise • Create truth tables of the following logical formulae: ¬(A∨B)∨¬A (A∧¬B)∧(A∨C) 11 Equivalence of logical formulae • Two logical formulae are equivalent if they have exactly the same truth table ¬(A∨B)∨¬A ⇔ ¬A 12 Logical operator for “implication” A → B • This expresses that “B must be true if A is true” A B A→B 0 0 1 1 0 1 0 1 1 1 0 1 ? 13 Logical operator for “equivalence” A ⇔ B • This expresses that “A and B are logically equivalent” A B A⇔B 0 0 1 1 0 1 0 1 1 0 0 1 14 Complete set of operators • A set of logical operators with which any logical formula can be equivalently expressed – Examples: • { NAND } • { NOR } • { NOT, AND } • { NOT, OR } 15 Proof and Inference Proof in propositional logic • Premises: A, B, C, … • Conclusion derived from premises: X • Proof in propositional logic is to show that (A∧B∧C∧…) → X is ALWAYS true 17 Method of proof (1) • Complete the truth table exhaustively and show that the formula is always true regardless of situations – Trivial, mechanistic method – Impractical if many variables are involved (due to explosion of possibility space) 18 Exercise • Prove “If A→(B→C), then (A→B)→(A→C)” by creating a truth table of this proposition 19 Method of proof (2) • Starting from unquestionably true “axioms”, keep modifying formulae based on logically sound inference rules until you reach what you want – Non-trivial, heuristic method – Potentially capable of proving complicated propositions through exploration – What humans usually do in math, physics – Reachable formulae are called “theorems” 20 Example: Hilbert-Bernays system • Made of 15 basic axioms and just 1 inference rule • The only inference rule: If A and A→B are both theorems, then B is also a theorem 21 Hilbert-Bernays axioms (1) I. Implication (1) A→(B→A) (2) (A→(A→B))→(A→B) (3) (A→B)→((B→C)→(A→C)) 22 Hilbert-Bernays axioms (2) II. Conjunction (1) A∧B→A (2) A∧B→B (3) (A→B)→((A→C)→(A→B∧C)) 23 Hilbert-Bernays axioms (3) III. Disjunction (1) A→A∨B (2) B→A∨B (3) (A→C)→((B→C)→(A∨B→C)) 24 Hilbert-Bernays axioms (4) IV. Equivalence (1) (A⇔B)→(A→B) (2) (A⇔B)→(B→A) (3) (A→B)→((B→A)→(A⇔B)) 25 Hilbert-Bernays axioms (5) V. Negation (1) (A→B)→(¬B→¬A) (2) A→¬¬A (3) ¬¬A→A 26 Hilbert-Bernays axioms (6) • Any formula that can be obtained by replacing A, B, and/or C in the basic axioms with other expressions is also an axiom – Example: A→(B→A) is an axiom, therefore (A→B)→(C→(A→B)) is also an axiom 27 Example of proof in HB system • Proving A∨A→A: Replace B in basic axiom I-(1) by A A→(A→A) Replace B in basic axiom I-(2) by A (A→(A→A))→(A→A) Apply inference rule to the above two formulae A→A Replace B and C in basic axiom III-(3) by A (A→A)→((A→A)→(A∨A→A)) Apply inference rule to the above two formulae ((A→A)→(A∨A→A)) Apply inference rule to the above and A→A A∨A→A 28 Exercise • Prove A∧B→A∨B in the HB system 29 Consistency, soundness, completeness • An axiomatic system is: – Consistent if it doesn’t prove any theorems that contradict to each other – Sound if its inference rules never produce false formula from true premises – Complete if it can prove or disprove all possible logical formula • HB system is known to be consistent, sound and complete within prop. logic 30 Automata and Formal Languages Logic vs. computation • Logic is a static description – It describes relationships between facts – It illustrates potential pathways leading to truth, but doesn’t tell where to go • Computation is a dynamic process – It executes specific operations in order – Computer (either machine or human) has its own internal states, I/Os, etc. 32 Automaton • A formal representation of dynamic, autonomous behaviors of machines • Has internal states • Changes its states and produces outputs over time according to predefined rules that refer to its own states and inputs received • States and time are usually discrete 33 Example • Parity checker – Tells whether the number of 1’s included in an input (bit string) is even or odd Initial state Even 1 Odd 1 0 0 34 Formal languages and automata • Formal language: An infinite set of strings that are grammatically valid – There are several distinct classes of grammatical complexity • Computational power of an automaton is often characterized by the class of languages it can recognize – After “hearing” a string, the automaton’s internal state tells whether that string is in the language or not 35 Chomsky’s hierarchy • Finite state automata • Can recognize regular languages • Pushdown automata • Can recognize context-free languages • Linear bounded automata • Can recognize context-sensitive languages • Turing machines • Can recognize recursively enumerable languages 36 Examples of languages • Regular languages: – { (01)n }, { bit strings in which 0’s and 1’s exist in even number each } • Context-free languages: – { 0n1n }, { bit strings in which 0’s and 1’s exist in the same number }, most programming languages • Context-sensitive languages: – { 0n1n2n }, most natural languages (weakly context-sensitive) 37 Finite state automaton • Has only finite number of states – Has no infinite memory • Therefore, all physically built computational systems are in this class in principle – Can recognize regular languages – Often used in complex systems modeling • E.g. cellular automata 38 Pushdown automaton • Finite state automaton with an infinitely long pushdown stack – Has infinite LIFO memory – Non-deterministic PDA can recognize context-free languages • Can handle nested structures inputs FSA 1 0 Pushdown stack 39 Linear bounded automaton • (Non-deterministic) Turing machine whose tape length is a linear function of the length of input – Has infinite memory but its accessible range is bounded according to input size – Can recognize context-sensitive languages 40 Turing Machines Turing machine (TM) • Finite state automata with an infinitely long memory tape – Has a read/write head that can move on the tape left and right B B 1 0 B FSA 42 Mathematical definition • Turing machine M: M=<S, S, f, q0, H> S: A finite set of states S: A finite set of tape symbols - Includes “B” for blank f: State-transition function - S x S → S x S × {R, L, N} (motion of head) q0: Initial state (in S) H: A set of halting states (subset of S) 43 Rule table f: State-transition function - S x S → S x S × {R, L, N} (motion of head) Often written as a set of “sss’s’m” – s: Current state of FSA – s: Symbol read from the tape – s’: Next state of FSA – s’: Symbol to be written to the tape – m: Direction of motion of the head 44 Computation by a Turing machine • Input: Initial contents of the tape • Output: Contents of the tape when the TM halts – TM halts when the FSA reaches one of its halting states Input BB10B q0 Computation (state transition) Output BB01B halt 45 Example a/1, → 1/1, → S = { q0, h }, S = { B, a, 1 } f = { q0aq01R, q01q01R, q0BhBL } q0 H = { h } B/B, ← Writing 1’s over Ba1aB h non-blank symbols moving rightward until it reaches a “B” q0 B11aB q0 B11aB q0 B111B q0 B111B h 46 Exercise • Design a Turing machine that moves its head rightward and keeps inverting bits written in its tape until its head reaches a blank symbol 47 Exercise • Figure out what the following TM does: S = { q0, e, o, h } S = { B, 1, E, O } f = { q01o1R, q0BhEN, e1o1R, eBhEN, o1e1R, oBhON } H = { h } 48 Computational Universality and Universal Turing Machines Computational universality of TMs • Church–Turing thesis: “Every mathematical function that is naturally regarded as computable is computable by a Turing machine” – Not a rigorous theorem or hypothesis, but an empirical “thesis” widely accepted TMs are considered “computationally universal” 50 Universal Turing machines (UTM) • More important fact shown by Turing: There are TMs that can emulate behaviors of any other TMs if instructions are given (software) A specific TM can be computationally universal just by itself! A B UTM C D 51 Intuitive reason • C-T thesis: TMs can compute any naturally computable process • It is possible to emulate the behavior of a certain TM using paper and pencil → Emulation of TMs is a naturally computable process! → It must be done by a TM too!! 52 The Halting Problem Then… • Is there any mathematical function that cannot be computed even by a Universal Turing Machine? Yes Functions for which no natural procedure of computation exists 54 Example: The halting problem • Given a description of a computer program and an initial input it receives, determine whether the program eventually finishes computation and halts on that input No • Is there a general procedure to solve this problem for any arbitrary programs and inputs? 55 Proof: Reductio ad absurdum (1) • Assume there is a general algorithm (and a TM) that can solve the halting problem for any program p and input i – Output of M: f(p, i) = 1 if program p halts on input i; 0 otherwise If p halts on i 1 Program p M If p doesn’t halt on i M Input i 0 (M always halts) M 56 Proof: Reductio ad absurdum (2) • One can easily derive another TM M’ from M so that it computes only diagonal components in the p-i space – Output of M’: f’(p) = f(p, p) If p halts on p 1 M’ Program p If p doesn’t halt on p M’ 0 (M’ always halts) M’ 57 Proof: Reductio ad absurdum (3) • One can further tweak M’ to make another TM M* that falls into an infinite loop if f’(p) = 1 – Output of M*: f*(p) = 0 if f’(p) = 0; doesn’t halt otherwise If p halts on p Program p M* M* M* doesn’t halt If p doesn’t halt on p 0 M* M* halts 58 Proof: Reductio ad absurdum (4) • What could happen if M* is given with its self-description p(M*)? Contradiction If p(M*) halts on p(M*) Program p(M*) M* M* M* doesn’t halt If p(M*) doesn’t halt on p(M*) 0 M* halts M* • Our initial assumption must be wrong: No general algorithm exists 59 Turing’s theorem • The halting problem of Turing machines is undecidable by Turing machines – Similar to Gödel’s incompleteness theorems, informally stated as: For any consistent, “powerful enough” axiomatic system, (1) there must be a statement that it can neither prove or disprove, and (2) its own consistency cannot be proven by itself 60 Example of statements that are neither provable nor disprovable “This statement is unprovable” – If the system proves this, it means that the system proves “This statement is unprovable” → contradiction – If the system disproves this, it means that the system proves that “This statement is unprovable” is provable → contradiction – Neither is possible! 61 Self-reference and dynamical systems • All of these messy things arise from “self-reference” • Logic is inherently static, but selfreference makes it a dynamic process that develops over time 62 Self-reference and dynamical systems • A “dynamic” view of logic: – An axiomatic system defines an infinitely large network of all possible logical expressions (nodes) connected by logical relationships – Truth values are states of nodes and propagates through inference – Incompleteness theorems say that the final attractor of this network must be non-stationary if the network includes self-referencing loops 63 Summary • Logic, proof and inference form the basis of mathematics and science • Computation is a dynamic form of logic, often modeled using automata – Their computational power can be associated to formal languages • Turing machines are most powerful and universal, yet some problems are not computable even by TMs 64