Download Nézondet`s p-destinies for theories with two and three quantifiers

Conference in Bedlewo (Poland)
21th of july – 27th of july 2012
In memoriam of professors
Henryk Kotlarski and Zygmunt Ratajczyk
Nézondet ‘s p-destinies for theories
with two and three quantifiers
The five missing numbers
Denis RICHARD, professeur émérite à l’Université d’Auvergne
1
The notion of p-destiny is due to Francis Nézondet
In his thesis (1997). Annie Château (2000) gave the best
written survey of this thesis in 2000 and also wrote the
first programm in CAML deciding Th2(N,S,⊥).
A group including YIN Jilei (Fudan DaXue), GUILLAUME
Marcel(Université Blaise Pascal) and DR (Université
d’Auvergne) attacked in 2005 the problem of constructing
the essential exhaustive tranverse destiny of Th3(N,S,⊥)
which would provide an algorithm of decision and an
axiomatisation of this theory. Therefore, there are
5 remaining cases. In each case it has to be construct
a number or to prove it does not exist.
2
0. What are p-destinies ?
0.1
The (trivial) 2-destiny Th2(N,S,P).
A p-destiny is a tree of height p of possibilities in a
theory with p quantifiers and a language L of
finitely many relations.
Suppose p=2 and N is the set of nodes of the tree and
take the predicates < and P for primeness.
We intend to obtain a description of all possible
(up to isomorphism) situations which can exist
with two variables.
3
Working with the tree of root 0 and denoting by a
circle the prime numbers, we get the
exhaustive 2-destiny of 0 inTh2(N,<,P)
Which , up to isomorphism, produce the following
essential 2-destiny of 0 in Th (N,<,P)
4
Of course, the same is possible for any integer, giving
the exhaustive simplified 2-destiny of Th2(N,<,P) :
5
Just keeping one representative for each class of
isomorphic trees, we can construct the so-call
exhaustive essential 2-destiny ( also called
essential tranverse 2- destiny) of Th2(N,<,P)
6
With the essential tranverse 2-destiny, we have
An algorithm of decision for Th2(N,<,P) : for
Q1x1 Q2x2 F(x1, x2)
The variable x1 takes its value(s) satisfying F(x1, x2)
on the roots of the trees (all values if Q1 is universal
and at least one value if Q1 is existential).
The same for x2 but at the depth 2.
The same essential tranverse 2-destiny provides an (trivial)
axiomatisation (more than 22 axioms) of Th2(N,<,P)
∃x(∃y⏋(y>x)∧ ⏋(x>y)))
∃x(∃y⏋(P(y)∧ (x<y)))
∃x(∃y(P(y)∧ (x<y)))
∃x( ∀ y(⏋(y<x)))
And so and …
7
0.2. Some definitions about p-destinies
Def. 0.2.1 (destiny). A p-destiny is a regular tree (X,P,r) of height p with a
structuration map c :
• X is the set of nodes of the tree
• P is the fatherhood relation
• R is the root of the tree
• c maps a L-structure denoted c(n) to a node n, with domain the branche
[r,n] so that if n1 and n2 are on a same branch, n1 being an ancestor of n2
then c(n1) is a substructure of c(n2)
Def. 0.2.2 (M-complete tree of height p). We call M-complete tree
of height p with root x the regular tree (LIST(M,p,x), P, (x)), where:
• (LIST(M,p,x) is the set of lists of elements of M with lenght at
most p reaching the root x
• the root (x) is the list with a unique element x
• P is the binary relation defined on the set of lists by x1P x2 iff x1
is the list x2 without its first element.
8
Def. 0.2.3 (induced canonical structuration) Let M be a L-structure and
x ϵ M. We define a structuration map c over (LIST(M,p,x),P,(x)) by the
following condition:
For every predicate R of L with arity k , for all families x1 = (y1,…),
x2 = (y2,…), …,(xk = (yk,…) of lists with respective first elements
y1,y2,…,yk belonging to the support of a same branch having z as a
leaf of the tree (LIST(M,p,x),P,(x)) , we have the following equivalence:
c(z) satisfies R(x1, x2, …,xk) iff M satisfies R(y1, y2, …,yk)
Def. 0.2.4 (exhaustive p-destiny) Let M be a L-structure p an integer
and x ϵ M. We define the exhaustive p-destiny of x as being the pdestiny :
(LIST(M,p,x),P,(x),c)
where (LIST(M,p,x),P,(x)) is the M-complete tree with height p and root
x, and c is the structuration canonical map induced on this tree by M.
9
Working with the tree of root 0 and denoting by a
circle the prime numbers, we get the
exhaustive 2-destiny of 0 in (N,<,P)
10
A stalk (pétiole in french) is a subtree of a destiny
equipped with the structuration induced by the
structuration of the whole destiny
Def. 0.2.5 (stalk isomorphism). An isomorphism of stalk
between two sub trees (resp. two destinies) is a bijection
preserving the tree structure (i.e. the fatherhood relation)
and being un isomorphism for the structuration map.
Def. 0.2.6 (superimposition (or simplification) of rank k )
Given a p-destiny (A,P,r,c), we say (A’,P,’r,’c’) is a
superimposition of rank k ( 0<k<p ) of this destiny, iff for
every node x, we have chosen a reprentative for every
isomorphism class of stalks for the stalks having as roots
the sons of x
11
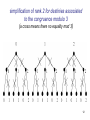
simplification of rank 2 for destinies associated
to the congruence modulo 3
(a cross means there no equality mod 3)
12
simplification of rank 2 for destinies
associated
to the congruence modulo 3
(a cross means there no equality mod 3)
13
Def. 0.2.7 (simplication of rank k and general simplification)
.
Given a family of superimpositions over the set of pdestinies of a fixed language Sj , Sj ,…, Sp-1, each with a
rank corresponding to its index, we call simplification at the
k rank, the map Sj o Sj … o Sp-1 . We call general
simplification a simplification at first rank.
Def. 0.2.8 (essential destiny). We call an essential
p-destiny or an essential tranverse p-destiny or a
tranverse p-destiny any range by a general
simplication of a p-destiny
14
Def. 0.2.8 (essential destiny). An essential p-destiny
is the range of a general (of rank p) simplification of a pdestiny
Transverse essential 2-destiny for the congruence modulo3
15
0.3 some reasons of becoming attached to p-destinies
• This the best possibility I know for effectively writing a programm
deciding a theory with fixed number of quantifiers and finitely many
relations (FRT),
• Destinies are good tools to test the truth in FRT to computers
• Destinies provide an axiomatization for FRT,
•Transform problems into the research of finitely many elements
determined by conditions,
• In the case of arithmetical theories, construction of destinies turns
• into finding integers realizing some conditions or does not exist.
• Destinies lead to the number-theoritical key-questions of a
theory , and focus on the actual expressive power of a FRT
• Use the powerful technic of FRAISSE-EHRENFURT back-and- forth in the steps of simplification
• Could be useful in data basis
16
Interlude : Why to choose relations S and ⊥ ??
Alan WOODS (1981) and DR (1982) gave independent proofs of
undecidability of Th(N, S, ⊥) and Th(N, =, S, ⊥).
Many interesting problems in number theory emerge from the thesis of
Alan Woods . One is now known as Erdös-Woods conjecture:
The following are equivalent:
(i) z=xy is (S, ⊥)- definable in N
(ii) z = x + y is (S, ⊥)- definable in N
(iii) x ⩽ y is (S, ⊥)- definable in N
(iv) x = y is (S, ⊥)- definable in N
(v) (Erdös-Woods Conjecture) There is some k >0 such that every
natural number x is determined uniquely by the sequence S0,
S1,…, Sk of sets of (distinct) prime numbers defined by Si = {p / p
divides x + i}
(vi) For any fixed prime p, the map n→pn is (S, ⊥) - definable in N.
17
Importance of EWC. Let us call Supp(a) the set of prime (distinct) divisors of a.
Consider the following conjectures of Number Theory :
Oesterlé-Masser’s conjecture. (Also called a-b-c conjecture) For all (a,b)
Î(N* )2 , there exists an effectively computable constant C such that :
Supp((a + b)ab) >
C[ (a+ b)/ gcd (a,b) ] 1-ε(a) with ε(a) tends to
0 when a tends to infinity.
Hall’s conjecture . Suppose x3 ≠ y2, for an effectively computable constant
C, we have
│ x3 − y2│> [C. Max (x3 , y2)] 1/ 6
Hall and Schinzel ‘s conjecture Suppose xm ≠ yn, for an effectively
computable constant C, we have
│ xm− yn│> [Max (x3 , y2)] C
M. Langevin results in [1988]
the three previous conjectures are false in case EWC fails
18
Moreover every conjecture which is false if Hall’s
conjecture is false, becomes false in turn if EWC is.
This is the case for
Lang-Waldschmidt‘s conjecture (which provides
lower bounds of linear forms of logarithms) and for
Vojta ‘s conjecture about abelian varieties.
Obviously a positive solution to one of this conjecture
would give a positive solution to EWC . More precisely
Hall and Schinzel‘s conjecture implies
that if a is sufficiently large, then a is
determined by So ,S1 , …, S20 .
19
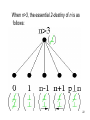
1) An algorithm of decision for Th2(N,S,⊥)
The root x can be or not coprime with x cannot be
in a relation of succession with x; for instance:
For a leaf k, there are relations of k to k and of k to x, : so that we have a
vector with 3 componenets as shown below ; the arrow from left to right
indicates x=S(k) and from right to left that k=S(x).
20
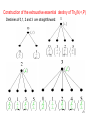
Construction of the exhaustive essential destiny of Th2(N,<,P)
Destinies of 0,1, 2 and 3 are straightforward:
21
When n>3, the essential 2-destiny of n is as
follows:
22
Now, it is easy to produce the essential exhaustive
transverse destiny of Th2(N,S,⊥) which provides
an algorithm of decision together with an
axiomatisation of this theory:
23
2) Results and questions on Th3(N,S,⊥)
As usual, le case with 3 is much more difficult than with 2
We denote Supp(n) the set of prime divisors of n.
Below for 3-destiny, n is the root of the tree, k is a son of x
and u a son of k
2.2) The nodes k and n are distant (S is not involved)
Then, there are 5 basis cases associated to u which are :
u = 0 is never coprime with an integer
u = 1 is coprime with any integer
u is not coprime to itself and coprime with k and n
u is not coprime to itself and coprime with k but not with n
u is not coprime to itself and coprime with n but not with k
24
Therefore, there are at most 5 branches (n,k,u) for u
far off from k and n for given k and n. The number of
branches depends on four relative positions of Supp(k)
and Supp(n) as follows:
Supp(k) ⊂ Supp(n) and Supp(k) ≠ Supp(n)
Supp(n) ⊂ Supp(k) and Supp(n) ≠ Supp(k)
Supp(n) = Supp(k)
Supp(n) \ Supp(k) ≠ ⍉ and Supp(k) \Supp(k) ≠ ⍉
In this situation 2.2, the 3-destinies are easy to construct
(cz14)
25
2.3) The node u is close to k or to n when k and n
are distant (S is involved)
Because u ϵ { k-1, k+1, n-1, n+1} and k-1, k+1 have
no successor link with n (similarly n-1, n+1 have no
successor relation with k), it remains to discuss the
coprimeness relationship between k-1, k+1 (resp.
n-1, n+1) with n (resp. k).
For each case, there are 2 possibilities so that the
number of possible cases is 16, giving the
following set of configurations of branches (n,k,u)
for u close to n or to k
26
27
Counting. For each (n,k) with n far off k, there
are 5 possibilities for the branches (n,k,u) when
u is distant from k and from n, and there are 16
possibilities for the branches (n,k,u) when u is
close to k or to n, so that we have 80 possible
stalks (pétiole in french) for n distant from k.
But each of these branches can or cannot appear
in the destiny of a given n , so that, a priori , there
are 280 trees in the essential tranverse destiny of
Th3(N,S,⊥)
Fortunately, we can enormously reduce the
number of possible trees.
28
2.4) Branches (n,k) when k is close to n
(S is involved)
We begin by n>3 (so that n-2 ≠0 and n-2 ≠1) .
The discussion is rather technical depending on the parity of n, and on
the combinatorial of Supp(n) and Supp(n-2) introducing the cases n=4,
n=6 , all numbers of the form
2(2α -1) and 2(2α +1)
After cleaning (n=4, …) the key-cases are the following :
⏋(n-3 ⊥ n) which appears iff n = 0 (mod 3) ;
⏋(n+1 ⊥ n-2) which appears iff n = 2 (mod 3);
(n - 3 ⊥ n) and (n+1 ⊥ n-2) which appears iff n = 1 (mod 3),
So that congruences modulo 3 appear in the construction
This is the first time, we observe Th3(N,S,⊥) depends of
exponents into the primary decomposition of integers and
the following cases appear
29
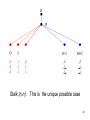
Stalk (n,n-2) : we know exactly when the cases
a, b, c, d and e appear or not (case k=n-2). There are 9
possible cases (excepting n=4 and n=5
30
Stalk (n,n-1) :
There are only 2 possible cases :
• (n is even and ⏋ (n-2 ⊥ n) (case a) or (n+1 ⊥ n-1)(case b)
• (n is odd and (n-2 ⊥ n) (case a) or ⏋ (n+1 ⊥ n-1) (case b)
31
Stalk (n,n) : This is the unique possible case
32
Stalk (n,n+1) : It is similar to the case k=n-1
• (n is even and (n-1⊥ n+1) (case a) or⏋(n+2 ⊥ n)(case b)
• (n is odd and⏋(n-1 ⊥ n+1) (case a) or (n+2 ⊥ n) (case b)
33
Stalk (n,n+2) : It is similar to the case k=n-2
34
(Pathological) cases of
Stalk(n,0) : here Supp(n) Supp(k)
Stalk(n,1) : 2 possibilities according the parity of n
Stalk(n,2) : Case a appears iff n=2α ; case b appears iff n is odd;
Case c appears iff n=0(mod3); case d and e appear iff n is odd
35
2.3 Counting all possibilities
Counting the cases when k is close to n and
the destinies of 0,1,2, we find 14 cases
Since 80 configurations was a majoration of the
cases for k distant from n, we have at most
14×280 possible destinies. What is huge
But in fact one can reduce to 646 cases allowing an
exhaustive inspection by a computer : Annie château
did it and proved the number of 3-destinies is at
most 72.
36
2.4 – Five open number theory questions necessary to
construct an essential transverse destiny of Th3(N, S, ⊥).
In fact , surprisingly, S and ⊥ do express properties of
the exponents of the prime factors of integers.
It turns out that two sets are the keys of our construction:
X = {nϵN /∃kϵN (Supp(k) ⫋Supp(n) ∧ (k-1⊥ n)∧ ⏋( k+1⊥ n)}
Y ={nϵN /∃kϵN (Supp(k) ⫋Supp(n) ∧ ⏋(k-1⊥ n)∧ ⏋( k+1⊥ n)}
This construction depends on the intersections of
{2
n
+1 / n ϵ N } and { 2
n
-1 / n ϵ N } with X and Y
This means an algorithm of decision through an essential transverse 3destiny will need to solve some questions in number theory
37
The work around these sets consists to find , for every form of n we
discuss previously ,
• a witness in X, or to prove there is no such integer
• a witness outside of Y, or to prove there is no such integer
• a witness in Y\X , or to prove there is no such integer.
Prop 1. (Characterization of Y) Y is the set of natural
integers having two distinct prime factors p and q such that
Ord(p,q) (the order of the element q within the group
(Z/pZ)* ) is even
Prop 2. (Characterization of X∩(2N+1)). A positive odd
integer belongs to X iff there is one of its prime divisors p,
and two integers b and c with disjoint supports included in
Supp(n) \ {p} such that v2(Ord(b,p) > v2(Ord(c,p)
More precisely, on the 9 questions sufficient to achieve the 3destiny, 5 remains open:
38
Sketch of the proofs
• Finite groups theory
• Quadratic reciprocity law
• Aurifeuille’s decomposition of numbers of the
form exp(2, ij2 α ) + 1.
The construction of the essential 3-destiny of
Th3(N, S, ⊥) depends on the answer
(by yes or no)
to nine questions
39
1) Is there a = ( 2n - 1) ∧│Supp (a)│= 2 ∧⏋(a in Y)
Answer :YES with a = 2227 - 1 or a = 2269 - 1
2) Is there a = ( 2n - 1) ∧│Supp (a)│= 2 ∧⏋(a in Y)
Answer : YES with a = 2(2269 - 1)
3) Is there a = ( 2n - 1) ∧│Supp (a)│⩾ 3 ∧⏋(a in Y)
OPEN
4) Is there a =( 2n + 1 ∧ n even ∧ │Supp (a)│= 2
∧⏋(a in Y) OPEN
5) = Is there a = ( 2n + 1) ∧ n even ∧ │Supp (a)│ ⩾ 3
∧⏋(a in Y) OPEN
40
6) = Is there a = ( 2n - 1) ∧ n odd∧│Supp (a)│⩾ 3 ∧
(a in Y\X) Answer: YES 225 -1 = 31.601.1801
7) = Is there a = ( 2n - 1) ∧ n even ∧│Supp (a)│ ⩾ 3
∧⏋(a in X)
Answer : NO
8) = Is there a = ( 2n + 1) ∧ n odd ∧ │Supp (a)│ ⩾ 3
∧⏋(a in X)
Answer : OPEN
9) = Is there a = ( 2n + 1) ∧ n even ∧ │Supp (a)│
⩾ 3 ∧⏋(a in Y\X) Answer : OPEN
41
Conclusion. To – day , we know 67 trees of this 3-destiny
(unpublished) which is made of at most 72 trees
42