Download Routing

CSS432 Routing
Textbook Ch 3.3
Instructor: Joe McCarthy
(based on Prof. Fukuda’s slides)
CSS 432: Routing
1
Forwarding vs. Routing

Forwarding:
 Maps
a network # to an outgoing
interface and some MAC information
 Sends a packet to an interface based
on a local and ~static forwarding table
 OSI Layer 2: data link level
 Implemented in specialized hardware
(switch)

Routing:
 Maps network # to its next hop
 Dynamically updated in a distributed
fashion based on network conditions
 OSI Layer 3: network level (IP)
 Implemented in software using
distributed algorithms
CSS 432: Routing
2
Network as a Graph
At Node A
A
6
1
3
4
C

9
F
1
D
Next Hop
B
2
E
C
6
E
D
2
E
E
1
E
F
3
E
Find lowest cost path between two nodes
Static approach has shortcomings:




B
E
Cost
Goal


2
1
Destination
Hardware may fail
Network topology may change
Bandwidth (cost) may change
Distributed, dynamic routing algorithms


Distance vector routing (RIP)
Link state routing (OSPF)
CSS 432: Routing
3
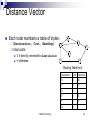
Distance Vector

Each node maintains a table of triples:


(Destination, Cost, NextHop)
Initial costs:


1, if directly connected to Destination
∞ otherwise
B
C
A
D
E
G
F
Routing Table for A:
CSS 432: Routing
Destination
Cost
Next hop
B
1
B
C
1
C
D
∞
-
E
1
E
F
1
F
G
∞
4
Distance Vector


Exchange updates with directly connected neighbors
 Every few seconds (periodic update)
 Whenever your table changes (triggered update)
Each update is a list of pairs:
 (Destination, Cost)







(C, 1, C) < (C, 2, B): new route is worse
(D, ∞, - ) > (D, 2, C): new route is better
From F: (G, 1)

D
G
F
From C: (D, 1)

C
A
E
Update local table if you receive a “better” route,
e.g., for A’s table:
 From B: (C,1)


From B: (A, 1), (C, 1)
From C: (A, 1), (B, 1), (D, 1)
From E: (A, 1)
From F: (A, 1), (G, 1)
B
(G, ∞, - ) > (G, 2, F): new route is better
Refresh existing routes; delete if they are expired
CSS 432: Routing
Routing Table for A:
Destination
Cost
Next hop
B
1
B
C
1
C
D
2
C
E
1
E
F
1
F
G
2
F
5
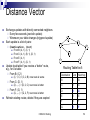
Distance Vector
Table 3.13 Distance vectors at each node
A
B
C
D
E
F
B
G
C
A
B
C
D
E
F
0
1
1
2
1
1
2
A
D
0
E
0
G
F
0
Routing Table for A:
0
0
G
0
[Each row is a distinct distance vector
stored at the node named in column 1]
CSS 432: Routing
Destination
Cost
Next hop
B
1
B
C
1
C
D
2
C
E
1
E
F
1
F
G
2
F
6
Distance Vector
Table 3.13 Distance vectors at each node
A
B
C
D
E
F
B
G
C
A
0
1
1
2
1
1
2
B
1
0
1
2
2
2
3
C
1
1
0
1
2
2
2
D
2
2
1
0
3
2
1
E
1
2
2
3
0
2
3
F
1
2
2
2
2
0
G
2
3
2
1
3
1
A
D
E
G
F
Routing Table for A:
Destination
Cost
Next hop
1
B
1
B
0
C
1
C
D
2
C
E
1
E
F
1
F
G
2
F
[Each row is a distinct distance vector
stored at the node named in column 1]
CSS 432: Routing
7
Routing Loops

Failure-recovering scenario
 F detects the link to G has failed
 F sets distance to G to ∞ and sends an update to A
 A sets distance to G to ∞
 A receives periodic update from C
with a 2-hop path to G
 A sets distance to G to 3 and sends update to F
 F sets distance to G in 4 hops via A
CSS 432: Routing
B
A
To G in 3
To G in 2
C
D
To G in 4
F
∞
E
To G in 1
G
8
Routing Loops


Failure-recovering scenario
 F detects the link to G has failed
 F sets distance to G to ∞ and sends an update to A
 A sets distance to G to ∞
 A receives periodic update from C
with a 2-hop path to G
 A sets distance to G to 3 and sends update to F
 F sets distance to G in 4 hops via A
Another scenario:
 The link from A to E fails
 A advertises distance of ∞ to E
A
B
To G in 3
A
To G in 2
C
D
E
To G in 4
F
∞
To G in 1
G
B
C
∞
E
CSS 432: Routing
9
Routing Loops


Failure-recovering scenario
 F detects the link to G has failed
B
C To G in 2
 F sets distance to G to ∞ and sends an update to A
To G in 3
A
D
 A sets distance to G to ∞
 A receives periodic update from C
E
To G in 1
To G in 4
with a 2-hop path to G
G
F
∞
 A sets distance to G to 3 and sends update to F
 F sets distance to G in 4 hops via A
B
Another scenario: Count-to-infinity problem
(5) To E in 4
(3) To E in 3
 The link from A to E fails
(2) To E in ∞
 A advertises distance of ∞ to E
(4) To E in ∞ (1) To E in 2
A
C
 C advertises a distance of 2 to E
(6) To E in 5
 B decides it can reach E in 3 hops (via C)
 B advertises this to A
∞
 A decides it can reach E in 4 hops (via B)
E
 A advertises this to C

C decides that it can reach E in 5 hops…
CSS 432: Routing
10
Loop-Breaking Heuristics


Use some finite maximum # (e.g., 16) instead of infinity

Scheme: Stop an infinity loop at 16.

Problem: Limited to 16 hops
Split horizon

Scheme: Don’t send a neighbor the routing information learned from
this neighbor


Ex. B includes (E, 2, A) and thus doesn’t send (E, 3) to A
Variation: Split horizon with poison reverse

Scheme: Send the routing information learned from this neighbor as
setting hop count (cost) to ∞.


Ex. B includes (E, 2, A) and thus sends (E, ∞, A)
Problem (with both variants): slow convergence speed
CSS 432: Routing
11
Routing Information Protocol (RIP)
frame header



Every 30 secs
Routing domain
Addr family (net addr)
Route tag
Address of Net 1
Cmd
Deleted in 60 secs
Used by Unix commands



Ver
Net 1 subnet mask
Next hop address (1-16)
Distance to Net 1
Addr family (net addr)
Route tag
Address of Net 2
Table entry timeout: 3 mins


Used by routers
Advertisement (periodic
update)


1: request
2: reply
UDP Port 520

RIP Message
UDP header
Cmd: 1-6


datagram heaader
ripquery (BSD)
25 entries
tcpdump (available in Linux, too)
CSS 432: Routing
snoop (Solaris)
Net 2 subnet mask
Next hop address
Distance to Net 2 (1-16)
12
Link State

Strategy
 Reliable dissemination of link-state information to
all nodes over a system.
 Calculation of routes from the sum of all the
accumulated link-state knowledge.

Link State Packet (LSP)
 ID of the node that created the LSP
 Costs of links to each directly connected neighbor
 Sequence number (SEQNO)
 Time-To-Live (TTL) for this packet
CSS 432: Routing
13
Link State

Reliable flooding: all nodes get LSPs from all other nodes
 Store most recent LSP from each node
 Forward LSP to all nodes but the one that sent it
 Generate new LSP periodically


Also generate LSP when link fails


Increment SEQNO (start with 0 upon reboot)
Detected via periodic “hello” packets
Decrement TTL of each received LSP


Also periodically decrement stored LSPs (“aging”)
Discard when TTL=0
CSS 432: Routing
14
Dijkstra’s Shortest-Path Algorithm
1.
2.
3.
Initialize Confirmed list with (myself, 0, -), Tentative with null list
For the node just added to the Confirmed list in the previous step,
call it node Next, select its LSP
For each neighbor (Neighbor) of Next, calculate the cost (Cost)
to reach Neighbor as the sum of the cost from myself to Next and
from Next to Neighbor


4.
If Neighbor is currently on neither the Confirmed nor the
Tentative list, then add (Neighbor, Cost, Nexthop) to the
Tentative list, where Nexthop is the direction I go to reach Next
If Neighbor is currently on the Tentative list, and the Cost is less
than the currently listed cost for Neighbor, then replace the
current entry with (Neighbor, Cost, Nexthop) where Nexthop is
the direction I go to reach Next
If the Tentative list is empty, stop. Otherwise, pick the entry from
the Tentative list with the lowest cost, move it to the Confirmed
list, and return to Step 2.
CSS 432: Routing
15
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
16
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
17
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
18
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
19
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
20
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
21
Dijkstra’s Shortest-Path Algorithm
CSS 432: Routing
22
Dijkstra’s Shortest-Path Algorithm

Alternative version (from original textbook slides):




N: set of nodes in the graph
l((i, j): the non-negative cost associated with the edge between
nodes i, j N and l(i, j) =  if no edge connects i and j
Let s N be the starting node which executes the algorithm to
find shortest paths to all other nodes in N
Two variables used by the algorithm



M: set of nodes incorporated so far by the algorithm
C(n) : the cost of the path from s to each node n
The algorithm
M = {s}
For each n in N – {s}
C(n) = l(s, n)
while ( N  M)
M = M  {w} such that C(w) is the minimum
for all w in (N-M)
For each n in (N-M)
C(n) = MIN (C(n), C(w) + l(w, n))
CSS 432: Routing
23
Dijkstra’s Shortest-Path Algorithm
Yet another alternative:
1 Initialization:
2 N' = {u}
3 for all nodes v
4
if v adjacent to u
5
then D(v) = c(u,v)
6
else D(v) = ∞
7
8 Loop
9 find w not in N' such that D(w) is a minimum
10 add w to N'
11 update D(v) for all v adjacent to w and not in N' :
12
D(v) = min( D(v), D(w) + c(w,v) )
13 /* new cost to v is either old cost to v or known
14 shortest path cost to w plus cost from w to v */
15 until all nodes in N'
CSS 432: Routing
Computer Networking:
A Top Down Approach
6th edition
Jim Kurose, Keith Ross
Addison-Wesley
March 2012
24
Open Shortest Path First Protocol (OSPF)
frame header
Version
Type(=4)
datagram header
OSPF header
Message Length
SourceAddr
AreaId
Checksum
Authentication type
Authentication 0-3
Authentication 4-7

OSPF Message
# of link status advertisements
Options
LS Age
Type=1
Link-state ID
Advertising router
LS sequence number
Link Checksum
Length
Type:
0 Flag
0
# of links
Hello (reachability)
2.
Database description (topology)
Link ID
3.
Link status request
Link data
4.
Link status update
5.
Link status acknowledgment
Metric
Link type Num TOS
Advertisement (header type=4)

LS Age: = TTL
Optional TOS information

Type=1: link cost between routers

Link-State ID = Advertising Router

Seq # from the same router

Link ID = the other end router ID of link

Link data = used if there are two or more links to the same router

Metric = link cost

Link type = P2P, ethernet, etc

TOS = delay-sensitive, etc
CSS 432: Routing
1.

25
OSPF Con’td


Gated daemon: directly uses IP datagram
Header Type2: Database description (topology)
message
 Used when the current
 Sent from an initialized
topology has changed.
router to another router which
has topology information

LS Sequence number
 Used
to determine which message is the latest
 Send a message with a new sequence number and
metric = ∞ when a router or a link fails.
CSS 432: Routing
26

Reviews
 RIP:
distance vector, routing loop and breaking heurictics
 OSPF: link state, Dijkstra’s shortest path algorithm

Exercises in Chapter 3
 Ex.
46 (RIP)
 Ex. 52 (RIP)
 Ex. 62 (OSPF)
 Ex. 64 (OSPF)
CSS 432: Routing
27
Ex 46

For the network shown in Figure 3.53, give global distancevector tables like those of Tables 3.10 and 3.13 when



(a) Each node knows only the distances to its immediate
neighbors
(b) Each node has reported the information it had in the
preceding step to its immediate neighbors.
(c) Step (b) happens a second time.
Table 3.13
CSS 432: Routing
28
Ex 52

Suppose we have the forwarding tables shown in
Table 3.16 for nodes A and F in a network where
all links have cost 1. Give a diagram of the
smallest network consistent with these tables.
Forwarding Table for F
Forwarding Table for A
Node
Cost
NextHop
Node
Cost
NextHop
B
1
B
A
3
E
C
2
B
B
2
C
D
1
D
C
1
C
E
2
B
D
2
E
F
3
D
E
1
E
CSS 432: Routing
29
Ex 62

Give the steps in the forward search
algorithm as it builds the routing database
for node A in the network shown in Figure
3.59.
CSS 432: Routing
30
Ex 64

Suppose that nodes in the network shown in Figure 3.61
participate in link-state routing, and C receives contradictory
LSPs: One from A arrives claiming the A-B link is down, but
one from B arrives claiming the A-B link is up.



(a) How could this happen?
(b) What should C do? What can C expect?
Do not assume that the LSPs contain any synchronized
timestamp.
CSS 432: Routing
31