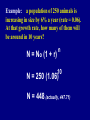* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lecture slides - (canvas.brown.edu).
Source–sink dynamics wikipedia , lookup
Storage effect wikipedia , lookup
Molecular ecology wikipedia , lookup
The Population Bomb wikipedia , lookup
Human overpopulation wikipedia , lookup
Two-child policy wikipedia , lookup
World population wikipedia , lookup
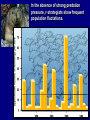
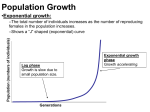
Bio 0200 Ecology I - Population Growth Principal Concepts Roots of the Science of Ecology Mathematics of Population Growth Limits: Carrying Capacity Survivorship & Life History Human Population Growth Predation & Life History • Labs begin Next Week. • Homework Assignment #2 (due Friday!) on web site. • Two “virtual” handouts today (Pop. Growth & Guppies) • Send e-mail today to request Lab Section. ecol-o-gy \ i-'klj\ n. pl. -gies [G kologie, fr. kec- + -logie -logy] (1858) 1. A branch of science concerned with the interrelationship of organisms and their environments. 2. The totality or pattern of relations between organisms and their environment. Species - collection of individuals interbreeding under natural conditions to produce fertile offspring, reproductive isolated from other such groups. (“biological species” definition) Population - individuals of the same species occupying a given area. Habitat - place where a population lives. Community - the population of all species interacting in a habitat. (including primary producers, and several levels of consumers) Ecosystem - a community and its physical and chemical environment Biosphere - the realm occupied by all living organisms on Earth Your textbook uses two slightly different notations for “discrete growth” & “continuous growth.” For accuracy and simplicity, we will use a single system, as described in the handout for today’s class. N = number of individuals in a population I = increase in population over a period of time I = births - deaths N = I = B - D t Determining birth and death rates: b= births N d= deaths N Because b and d are rates, they automatically include the unit of time over which the data were collected (per year, per month, etc…) Population Growth - an Example: In a town of 1,000 people, over the course of a year 46 babies are born, and 36 people die. Increase: I = 10 Birth Rate: b = 46 / 1000 = 0.046 Death Rate: d = 36 / 1000 = 0.036 And, we can determine a new value that takes births and deaths into consideration: the net Rate of Population Growth, r: r=b-d r = 0.046 - 0.036 = 0.010 Suppose that we know the rate of population growth (r) and we'd like to figure out how much that population will increase over a period of time. To determine the increase to be expected we simply multiply r by the size of the population (N): I = rN I = 0.010 x 1000 = 10 We could also ask the question in a slightly different way. How large is the population at the end of a year when the growth rate (r) is 0.010? N = No + I (or) N = No + rNo N = 1000 + (0.010 x 1000) = 1000 + 10 = 1010 If we wanted to do this over several years, we could run this equation for each and every year: N = No + rNo Or, we could simplify the equation: N = No + rNo N = No (1 + r) And then, we could simply place an exponent over the bracketed term... allowing the equation to apply for any number of years (or intervals): N = No (1 + r) n Example: a population of 250 animals is increasing in size by 6% a year (rate = 0.06). At that growth rate, how many of them will be around in 10 years? N = No (1 + r) n 10 N = 250 (1.06) N = 448 (actually, 447.71) Key Point: Although birth rates are (of course) affected by death rates, so long as r is positive, the population will always grow in an exponential fashion: - growth of bacteria in a flask. - doubling occurs every 30 minutes - place 1 bacterium in flask - after 10 hours: 1,048,576 bacteria - at the end of 20 hours: 1.0995116 x 1012 - After 2.5 days? Mass of bacteria exceeds mass of Earth! Key Point: Although birth rates are (of course) affected by death rates, so long as r is positive, the population will always grow in an exponential fashion: bacteria Question: What happens if there’s a 10 or 20% death rate between generations? No deaths 10% die between doublings 25% die between doublings Freeman 3/e Fig. 52.5 High r Moderate r Low r Key Point: Exponential growth occurs at any value of r ... so unchecked growth will eventually produce high population density. Even though exponential growth can be observed under certain conditions . . . . . . eventually such growth is stopped under real conditions. What stops it? Survival declines at high population density Fecundity declines at high population density Density-Dependent checks on Population Growth • Birth and death rates usually fluctuate in response to population density; that is, they are densitydependent. • As a population increases in size, it may deplete its food supply, reducing the amount of food each individual gets. Poor nutrition may increase death rates and decrease birth rates. • If predators are able to capture a larger proportion of the prey when prey density increases, the per capita death rate of the prey rises. • Diseases, which may increase death rates, spread more easily in dense populations than in sparse populations. Density-Independent checks on Population Growth • Factors that affect birth and death rates in a population independent of its density are said to be densityindependent. • Severe weather (like a cold winter) may kill large numbers of a population regardless of its density. • Other examples: some diseases, earthquakes, volcanic eruptions, floods, storms. Exponential growth only occurs under idealized (unlimited) conditions Real conditions always seem to approach a limit: We call this apparent limit a “Carrying Capacity.” (environmental resistance) Carrying Capacity (biotic potential) Equilibrium Exponential Growth Growth starts out exponential: and then seems to approach a limit: This means that the observed growth rate (r) varies throughout this curve. Early on, it seems purely exponential. Later, it seems limited. Can we use math to model these characteristics? I = ro N ro = Intrinsic Growth Rate (maximum growth rate). “The rate observed in the presence of unlimited resources.” Also: rmax (in your text) Important! The intrinsic rate (ro) is generally close to (or identical to) the observed rate (r) during the early (non-limited) phase of population growth. We can model what happens in the later phase by assuming that the system has a carrying capacity (K) ... What it represents does this the proportion of unexploited actually resources in K. represent? K I = ro N [ K-N K ] N K-N = rmax N t K [ ] I = ro N [ K-N K ] What happens when N is much smaller than K? What happens when N is 1/2 the value of K? What happens when N is nearly as big as K? What happens when N exceeds the carrying capacity (K)? Part of your homework assignment is to work with a simple logistic growth model... ... and then to record and explain your results. (The model is accessed from the Week 2 web page) The distinct effects of “r” (growth rate) and “K” (carrying capacity) on populations give rise to two general “strategies” of long-term survival: R-strategists: many offspring, little care, fast maturity (reliance on fast growth: “r”) K-strategists: few offspring, plenty of care, slow maturity. K-strategists: few offspring, plenty of care Type I Type II Type III R-strategists: many offspring, little care In the absence of strong predation pressure, r-strategists show frequent population fluctations. So do K-strategists (over a longer term) Pribilof Is. THE INTRODUCTION, INCREASE, & CRASH OF REINDEER ON ST. MATTHEW ISLAND David R. Klein Alaska Cooperative Wildlife Research Unit, University of Alaska What provides for long-term stability in a population of consumers? What provides for long-term stability in a population of consumers? A key study of natural populations: • guppies in two small streams in Trinidad, as studied by David Reznick and his associates (UC Riverside): killifish ~ 3 cm Pike cichlid ~ 30 cm The pike cichlid doesn’t chase small, immature guppies (which it seldom catches anyway). The pike concentrates on the largest guppies in the stream The killifish preys upon the smaller guppies. Mature fish are too big for it to take on. Guppies in the pikecichlid stream are smaller (male & female) at sexual maturity. Guppies in the pikecichlid stream reproduce more quickly, and produce smaller embryos. Small predator (killifish). Attacks only small, immature fish. Effects on life history: Guppies mature later, females are large, produce larger eggs and embryos. Rationale: Once out of danger, best reproductive strategy is to produce larger eggs that will outgrow the predator as quickly as possible. Large predator (Pike-cichlid) attacks large, mature fish. Effects on life history: Guppies mature earlier, females are small, produce smaller eggs and embryos, reproduce more frequently. Rationale: Since maximum danger comes at maturity, mature more quickly and reproduce as often as possible (with smaller eggs). Transplantation experiments confirm that a change in predator eventually results in a change in life cycles. • Life History Patterns are heritable. • They show variation within a population. • The variants best able to evade the predator will be most successful in reproduction. • Over time, the effects of the predator will change the life history pattern of the fish population.