* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download the notes
Degrees of freedom (statistics) wikipedia , lookup
Foundations of statistics wikipedia , lookup
Psychometrics wikipedia , lookup
History of statistics wikipedia , lookup
Confidence interval wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Omnibus test wikipedia , lookup
Regression toward the mean wikipedia , lookup
Taylor's law wikipedia , lookup
Misuse of statistics wikipedia , lookup
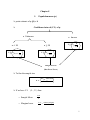
Kuwait University College of Business Administration Department of Quantitative Methods and information System Tutorial Stat 220 Chapter 7: sampling and sampling distribution Chapter 8: confidence interval Chapter 9: hypothesis testing Chapter 10: statistical inference based on two samples Chapter 11: ANOVA Chapter 12: chi-square test for independence Chapter 13: simple linear regression Chapter 14: multiple regression and model building Done by: T.A Dalal Al-Odah T.A Narjes Akbar T.A Dalal AL-Banwan Supervised by Dr.Mohammed Qadry Grraph summer 2014/2015 1 Chapter 7 I. ̅ Sampling distribution of sample mean 𝒙 Exactly normal Approximately normal If the population data follow Normal (𝜇, 𝜎) Then If the population data follow any distribution (not normal) and the sample size is large (𝑛 ≥ 30) Then The sampling distribution 𝜎 𝑥̅ ~𝑁 (𝜇𝑥̅ = 𝜇, 𝜎𝑥̅ = ) √𝑛 The sampling distribution 𝜎 𝑥̅ ~𝑁 (𝜇𝑥̅ = 𝜇, 𝜎𝑥̅ = ) √𝑛 (by central limit theorem CLT) Where: 𝑥̅ : Sample mean 𝑍= 𝑥̅ − 𝜇 𝜎 √𝑛 𝜇: Population mean 𝜎: Population standard deviation 𝜎𝑥̅ : Standard deviation of the sample mean (standard error) 𝜇𝑥̅ : mean of the sample mean Note: mean = average = rate = expected 2 EXERCISES 1. The amounts of electric bills for all households in a city have a skewed probability distribution with a mean of $80 and a standard deviation of $25. Let 𝑥̅ be the mean amount of electric bills for a random sample of 75 households selected from this city. Find: a. The mean of the sampling distribution of 𝑥̅ b. The variance of the sampling distribution of 𝑥̅ c. The standard deviation (error) of the sampling distribution of 𝑥̅ d. What is the sampling distribution of the sample mean 𝑥̅ e. Find the probability that the mean amount of electric bills for a random sample of 75 households selected from this city will be i. Between $72 and $77 ii. Within $6 of the population mean iii. More than the population mean by at least $5 iv. Less than the population mean by at least $2 v. Either less than $72 or more than $77 3 2. The print on the package of 100-watt General Electric soft-white light bulbs claims that these bulbs have an average of 750 hours. Assume that the lives of such bulbs have a normal distribution with a mean of 750 hours and a standard deviation of 55 hours. Let 𝑥̅ be the mean life of a random sample of 25 such bulbs. a. Find the mean and standard deviation of 𝑥̅ and describe its sampling distribution. b. Find the probability that the mean life of a random sample of 25 such bulbs will be within 15 hours of the population mean. c. Find the fraction that 𝑥̅ will be less than the population mean by 20 hours or more. d. Find the percentage that 𝑥̅ will be more than the population mean by at least 20 hours. e. Find the probability that 𝑥̅ will be within 1.5 standard deviation (error) of the population mean. REVIEW 1. A quality control inspector periodically checks a production process. This inspector selects simple random samples of 30 finished products and computes the sample mean product weights ̅𝑥. Test results over long period of time show that 2.5% of the 𝑥̅ values are over 2.1 kg and 2.5% are less than 1.9 kg. a. What are the mean and standard deviation for the population of products produced with this process? (𝝁 = 𝟐, 𝝈 = 𝟎. 𝟐𝟕𝟗𝟓). b. Find the probability that 𝑥̅ will be within one standard deviation (error) of the population ̅ ≤ 𝝁 + 𝝈𝒙̅ ) = 𝒑(−𝝈𝒙̅ ≤ 𝒙 ̅ − 𝝁 ≤ 𝝈𝒙̅ ) = 𝒑(−𝟏 ≤ 𝒛 ≤ 𝟏) = 𝟎. 𝟔𝟖𝟐). mean?(𝒑(𝝁 − 𝝈𝒙̅ ≤ 𝒙 2. A machine makes 3-inch-long nails. The probability distribution of the lengths of these nails is normal with a mean of 3 inches and a standard deviation of 0.1 inch. The quality control inspector takes a sample of 25 nails once a week and calculates the mean length of theses nails. If the mean of this sample is either less than 2.95 inches or greater than 3.05 inches, the inspector concludes that the machine needs an adjustment. a. What is the mean, standard deviation (error) and sampling distribution of the sample ̅~𝑵(𝝁𝒙̅ = 𝟑, 𝝈𝒙̅ = 𝟎. 𝟎𝟐)) mean?(𝒙 b. What is the probability that based on a sample of 35 nails the inspector will conclude that the ̅ < 𝟐. 𝟗𝟓) + 𝒑(𝒙 ̅ > 𝟑. 𝟎𝟓) =. 𝟎𝟎𝟑) machine needs an adjustment?(𝒑(𝒙 4 II. ̂ Sampling distribution of the sample proportion 𝑷 Approximately normal If 𝑛𝑃 ≥ 5 and 𝑛(1 − 𝑃) ≥ 5 Then The sampling distribution 𝑃̂~𝑁(𝜇𝑃̂ = 𝑃, 𝜎𝑃̂ = √ 𝑃(1 − 𝑃) ) 𝑛 (by central limit theorem CLT) Where: 𝑍= 𝑃̂ − 𝑃 √𝑃(1 − 𝑃) 𝑛 𝑃: Population proportion 𝑃̂: Sample proportion 𝜇𝑃̂ : Mean of the sample proportion 𝜎𝑃̂ : Standard deviation of the sample proportion (standard error) 5 EXERCISES 1. A corporation makes auto batteries. The company claims that 80% of its batteries are good for 70 months or longer. Assume that this claim is true. Let 𝑃̂ be the proportion in a sample of 100 batteries that are good for 70 months or longer. a. What is the mean, standard deviation (error), and sampling distribution of the sample proportion? b. The probability that the proportion is less than 0.09? c. The probability that this 𝑃̂ is within 0.05 of the population proportion? d. The probability that this 𝑃̂is not within 0.05 of the population proportion? e. What is the probability that 𝑃̂ is less than the population proportion by 0.06 or more? REVIEW 1. Suppose that among the undergraduate students at a very large university 5.9% are international students and 57.8% are female. a. If 28 students are randomly sampled, what is the probability that fewer than 14 are 𝒙 𝟏𝟒 ̂𝒇 < 𝟎. 𝟓) = 𝑷(𝒛 < −𝟎. 𝟖𝟒) = 𝟎. 𝟐𝟎𝟎𝟓). female?(𝑷(𝒙𝒇 < 𝟏𝟒) = 𝑷 ( 𝒏𝒇 < 𝟐𝟖) = 𝑷(𝒑 b. If 10 students are randomly sampled, what is the probability that more than 10% are ̂ 𝑰 > 𝟎. 𝟏) = 𝑷(𝒛 > 𝟎. 𝟓𝟓) = 𝟎. 𝟐𝟗𝟏𝟐). international students?(𝑷(𝑷 2. A machine that is used to make CDs is known to produce 6% defective CDs. The quality control inspector selects a sample of 100 CDs every week and inspects them for being good or defective. If 8% or more of the CDs in the sample are defective, the process is stopped and the machine will be adjusted. What is the probability that based on a sample of 100 CDs the process will be ̂ > 𝟎. 𝟎𝟖) = 𝑷(𝒛 > 𝟎. 𝟖𝟑) = 𝟎. 𝟐𝟎𝟑𝟑). stopped to adjust the machine?(𝑷(𝒑 6 Chapter 8 I. Population mean (𝝁) ̅ ̂) = 𝒙 point estimate of 𝜇 (𝝁 Confidence interval (C.I.) of 𝝁 𝜎 Unknown 𝜎 known 𝑛 ≥ 30 𝑛 < 30 𝑥̅ ± 𝑡𝛼⁄2,𝑛−1 𝑠 𝑥̅ ± 𝑍𝛼⁄2 √𝑛 𝑥̅ ± 𝑍𝛼⁄2 𝜎 √𝑛 𝑠 √𝑛 Margin of Error (Max Error/ Error) To fine the sample size 𝑍𝛼⁄2 𝑠𝑡𝑑. 𝑑𝑒𝑣 2 𝑛=( ) 𝐸 If we have C.I. ( L , U ) then o Sample Mean o Marginal error 𝐿+𝑈 2 𝑈−𝐿 2 = 𝑤𝑖𝑑𝑡ℎ (𝑙𝑒𝑛𝑔𝑡ℎ) 2 7 Exercises: 1. A random sample of 16 mid-sized cars, which were tested for fuel consumption, gave a mean of 26.4 miles/gallon with standard deviation of 2.3 miles/gallon. a. Find a 95% confidence interval for the average fuel consumption of a midsized car? b. What assumption(s) are necessary for your answer in (a) to be valid? c. Find the error of such interval? d. If we choose a sample of size 100 mid-sized cars, then repeat part (a)? e. What sample size would be required to reduce the margin of error by 50%? 2. An economist wants to find a 90% confidence interval for the mean sale price of houses in a state. How large a sample should he or she select so that the estimate is within $3500 of the population mean? Assume that the standard deviation for the sale prices of all houses in this state is $31500? 8 3. IQ tests are designed to yield results that are approximately normally distributed. Researchers think that the population standard deviation is 15. A reporter is interested in estimating the average IQ of employees in a large high-tech firm in California. She gathers the IQ information on 22 employees of this firm and records the sample mean IQ as 106. a. Compute 90% confidence intervals of the average IQ in this firm. b. If the C.I is (97.77, 114.23) find the confidence level 4. In analyzing the operating cost for a huge fleet of delivery trucks, a manager takes a sample of 25 cars and calculated the sample mean and variance of the operating cost. Under the assumption that the operating cost has a normal distribution, he found that the 95% confidence interval for the mean operating cost is between 253 and 300 K.D. a. Find the maximum error of estimate (error bound) for such interval? b. Find the sample mean and variance? c. The manager said he is 95% confidence that the sample mean lies within such interval, do you agree? Why? d. Construct a 90% confidence interval for the true mean? Find the error of such interval? 9 Review: 1. To measure the time taken to manufacture a device, a random sample was chosen. The following is the assembly time (the time taken to fix each device in minutes ) for the sample: 8 10 12 15 17 If the sample information is used to estimate the population mean of the assembly time then: a. Give a point estimate and a 99% confidence interval for the population mean? ∑ 𝒔 State your necessary assumptions we need?(𝝁̂ = 𝒙̅ = 𝒏𝒙 = 𝟏𝟐. 𝟒, 𝒙̅ ± 𝒕𝜶⁄𝟐,𝒏−𝟏 √𝒏 , 𝒂𝒔𝒔𝒖𝒎𝒑𝒕𝒊𝒐𝒏 𝒊𝒔 𝒏𝒐𝒓𝒎𝒂𝒍 𝒑𝒐𝒑𝒖𝒍𝒂𝒕𝒊𝒐𝒏 ). b. If the population standard deviation is known to be 3, how large is the sample size needed to estimate the mean assembly time with 0.99 confidence, and error margin of one minute?(𝒏 = ( 𝒁𝜶⁄ 𝝈 𝟐 𝟐 𝑬 ) =( 𝟐.𝟓𝟕𝟔×𝟑 𝟐 𝟏 ) = 𝟓𝟗. 𝟕𝟐 ≅ 𝟔𝟎) 2. Determine the margin of error for a confidence interval estimate for the population mean of a normal distribution given the following information: Confidence level=0.98, n=13, S=15.68 (𝑴. 𝑬 = 𝟏𝟏. 𝟔𝟔) 10 II. Population proportion Point estimate of P= 𝑃̂ Confidence interval of P 𝑃̂ (1 − 𝑃̂) 𝑃̂ ± 𝑍𝛼⁄2 √ 𝑛 Margin of Error (Max Error/ Error) To find the sample size 𝑛=( 𝑍𝛼⁄ 2 𝑝̂𝑞̂ 2 𝐸2 ) Where 𝑞̂ = 1 − 𝑝̂ 11 Exercises: 1. It is said that happy and healthy workers are efficient and productive. A company that manufactures exercising machines wanted to know the percentage of large companies that provide on-site health club facilities. A sample of 240 such companies showed that 96 of them provide such facilities on site. a. What is the point estimate of the percentage of all such companies that provide such facilities on site? What is the margin of error associated with this point estimate? b. Construct a 97% C.I for the percentage of all such companies that provide such facilities on site. 2. A consumer agency wants to estimate the proportion of all drivers who wear seat belts while driving. Assume that a preliminary study has shown that 76% of drivers wear seat belts while driving. How large should the sample size be so that the 99% C.I for the population proportion has a maximum error of 0.03? 3. A college registrar has received complaints about the online registration procedure at her college. She wants to estimate the proportion of all students at this college who are dissatisfied the online registration procedure. What is the most conservative estimate of the sample size that would limit the maximum error to be within 0.05 of the population proportion for 90% C.I? 12 Review 1. A researcher wanted to know the percentage of judges who are in favor of the death penalty. He took a random sample of 15 judges and asked them whether or not they favor of the death penalty. The responses of these judges are given here Yes No Yes Yes No No No Yes Yes No Yes Yes Yes No Yes a. What is the point estimate of the population proportion? What is the margin of ̂ ̂ ̂ = 𝒙 = 𝟎. 𝟔, 𝑴. 𝑬 = 𝒁𝜶⁄ √𝑷(𝟏−𝑷) = 𝟎. 𝟐𝟒𝟕𝟗) error associated with this point estimate?(𝑷 𝟐 𝒏 𝒏 b. Make a 95% C.I for the percentage of all judges who are in favor of the death penalty.(𝟎. 𝟔 ± 𝟎. 𝟐𝟒𝟕𝟗𝟐) 2. a. How large a sample should be selected so that the maximum error of estimate for 99% C.I for the population proportion is 0.035? When the value of the sample proportion obtained from a preliminary sample is 0.29?(𝟎. 𝟐𝟗±. 𝟎𝟑𝟓) b. Find the most conservation sample size that will produce the maximum error for a 99% C.I for p equal to 0.035(𝑯𝒊𝒏𝒕: 𝑖𝑓 𝑝̂ 𝑛𝑜𝑡 𝑔𝑖𝑣𝑒𝑛 𝑡𝑎𝑘𝑒 𝑝̂ = 0.5, 𝒏 = 𝟏𝟑𝟓𝟒. 𝟐𝟓 ≅ 𝟏𝟑𝟓𝟓) 13 Chapter 9 I. Testing hypothesis for 𝝁 1. State null hypothesis (𝐻0 ) and alternative hypothesis (𝐻1 ) 𝐻0 : 𝜇 = 𝐻1 : 𝜇 ≠ < > vs ≥ ≤ T.S for 𝜇 2. Calculate the test statistic (T.S) 𝜎 𝑢𝑛𝑘𝑛𝑜𝑤𝑛 𝑛 < 30 𝑇𝐶 = 𝜎 𝑘𝑛𝑜𝑤𝑛 𝑍𝐶 = 𝑛 ≥ 30 𝑥̅ − 𝜇 𝑠 √𝑛 𝑍𝐶 = 𝑥̅ − 𝜇 𝑠 √𝑛 𝑥̅ − 𝜇 𝜎 √𝑛 3. Calculate P-value 3. Determine the rejection region (R.R) p-value + p-value + −𝑍𝛼⁄ 2 𝑍𝛼⁄ 2,𝑛−1 𝑡𝛼⁄2,𝑛−1 −𝑡𝛼⁄ 2 Two-Tailed −𝑍𝛼 −𝑡𝛼,𝑛−1 Left-Tailed 4. Conclusion: we reject 𝐻0 if T.S lies in the R.R p-value 𝑍𝛼 𝑡𝛼,𝑛−1 Right-Tailed −𝑍𝐶 𝑍𝐶 Two-Tailed −𝑍𝐶 𝑍𝐶 Left-Tailed 4. Conclusion: we reject 𝐻0 if 𝑝𝑣𝑎𝑙𝑢𝑒 < 𝛼 Right-Tailed 14 Type І error: o What is the type І error? 𝑅𝑒𝑗𝑒𝑐𝑡 𝐻0 / 𝐻0 𝑖𝑠 𝑡𝑟𝑢𝑒 o What is the probability of type І error? P (type І error) = α = 𝑃(𝑅𝑒𝑗𝑒𝑐𝑡 𝐻0 / 𝐻0 𝑖𝑠 𝑡𝑟𝑢𝑒) o Note: 1 − 𝛼 = 𝑃(𝑑𝑜 𝑛𝑜𝑡 𝑟𝑒𝑗𝑒𝑐𝑡 𝐻0 /𝐻0 𝑖𝑠 𝑡𝑟𝑢𝑒) Type П error: o What is the type П error? 𝐷𝑜 𝑛𝑜𝑡 𝑟𝑒𝑗𝑒𝑐𝑡 𝐻0 / 𝐻0 𝑖𝑠 𝑓𝑎𝑙𝑠𝑒 o What is the probability of type П error? P (type П error) = β= 𝑃(𝐷𝑜 𝑛𝑜𝑡 𝑟𝑒𝑗𝑒𝑐𝑡 𝐻0 / 𝐻0 𝑖𝑠 𝑓𝑎𝑙𝑠𝑒) o Note: 1 − 𝛽 = 𝑃( 𝑅𝑒𝑗𝑒𝑐𝑡 𝐻0 /𝐻0 𝑖𝑠𝑓𝑎𝑙𝑠𝑒) Power of the test The null hypotheses is Your Decision based on a random sample true false Reject Type І error Correct decision Do not Reject Correct decision Type П error 15 Exercises: 1. According to survey by the national retail Association, the average amount that households in the United States planned to spend on gifts, decorations, greeting cards, and food during 2001 holiday season was $940. Suppose that a recent random sample of 324 households showed that they plan to spend an average of $1005 on such items during this year’s holiday season with a standard deviation of $330. a. Test at the 1% significance level whether the mean of such planned holiday related expenditures for households for this year differs from $940. 1) 2) 3) 4) b. Find 99% C.I of µ. c. Use C.I from part (b) to test 𝐻0 : 𝜇 = 940 𝑣𝑠 𝐻1 : 𝜇 ≠ 940 16 2. A drug company is considering marketing a new local anesthetic. The effective time of the anesthetic the drug company that is currently produced has a normal distribution with an average of 7.4 minutes with standard deviation of 1.2 minutes. To market the new anesthetic, the mean effective time should be less than 7.4 min. a sample of size 36 results in a sample mean of 7.1. a hypothesis test will be done to help make a decision. a. State the null and the alternative hypotheses b. Compute the test statistic c. Compute the P-value of the test d. What is your recommendation to the drug company using a level of significance of 0.01? 3. Insurance companies track life expectancy information to assist in determining the cost of life insurance policies. Last year the average life expectancy of all policyholders was 77 years. A company wants to determine if their clients now have longer life expectancy on average, so they randomly sample 20 of their recent paid policies. The sample has a mean of 78.6 years and a standard deviation of 4.48 years. a. Write the null and alternative hypotheses b. What is the value of the test statistic? c. State your conclusion using 𝛼=0.05 d. Considering the result of the test, which type of errors in hypothesis testing could you have made? e. State your assumptions 17 II. Testing hypothesis for P 1. State null hypothesis (𝐻0 ) and alternative hypothesis (𝐻1 ) 𝐻0 : 𝑃 = vs 𝐻1 : 𝑃 ≠ < ≥ > ≤ 2. Calculate the test statistic (T.S) T.S for 𝑃 𝑍𝐶 = 𝑃̂ − 𝑃 √𝑃(1 − 𝑃) 𝑛 3. Calculate P-value 3. Determine the rejection region (R.R) p-value + p-value + −𝑍𝛼⁄2 𝑍𝛼⁄2 Two-Tailed −𝑍𝛼 Left-Tailed 𝑍𝛼 Right-Tailed −𝑍𝐶 𝑍𝐶 Two-Tailed 4. Conclusion: we reject 𝐻0 if T.S lies in the R.R p-value −𝑍𝐶 𝑍𝐶 Left-Tailed 4. Conclusion: we reject 𝐻0 if 𝑝𝑣𝑎𝑙𝑢𝑒 < 𝛼 Right-Tailed 18 Exercises: 1. A food company is planning to market a new type of frozen yogurt. However, before marketing this yogurt, the company wants to find what percentage of the people like it. The company’s management has decided that it will market this yogurt only if at least 35% of the people like it. The company’s research department selected a random sample of 400 persons and asked them to taste this yogurt. Of these 400 persons, 112 said they like it. a. Testing at the 2.5% significant level, can you conclude that the company should market this yogurt? 1) 2) 3) 4) b. What will your decision be in part (a) if the probability of making a type І error is zero? 2. A study by consumer reports showed that 64percent of supermarket shoppers believes supermarket brands to be as good as national name brands. a. Formulate the hypotheses that can be used to determine whether the percentage of supermarket shoppers who believe that supermarket brands to be as good as national name brands is different from 64%. b. If a sample of 100 shoppers showed that 52 stating that the supermarket brand was as good as the national brand, what is the value of the test statistic? 19 c. What is the p-value? d. At 𝛼 =0.05, what is your conclusion? Justify your answer. 3. Suppose that in a sample of 1000 employees 23% said that losing their job is the major reason of concern for them. a. Find a 98% confidence interval for the percentage of employees who said losing their job is the major reason of concern for them. b. According to your confidence interval obtained in (a) do you believe that percentage is different from 19% and why or why not? Review: 1. The policy of a company is to deliver on time at least 90% of all the orders it receives from its customers. The quality control inspector at the company usually takes samples of orders delivered and checks if this policy is maintained. A sample of 90 orders taken by this inspector showed that 75 of them were delivered on time. At the 2% significance level, can you conclude that the company’s policy is maintained? Use the p-value to conduct the test.(𝑯𝟏 : 𝑷 < 𝟎. 𝟗, 𝒁𝒄 = −𝟐. 𝟐𝟏, 𝒑 − 𝒗𝒂𝒍𝒖𝒆 = 𝟎. 𝟎𝟏𝟑𝟔, 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ). 20 one population variance 𝝈𝟐 III. Point estimate for one population variance 𝜎 2 one population st. deviation 𝜎 𝑆2 𝑆 Confidence interval for One population variance 𝜎 2 One population St. Deviation 𝜎 (𝑛 − 1)𝑠 2 (𝑛 − 1)𝑠 2 2 <𝜎 < 2 𝑥𝛼2⁄ ,𝑛−1 𝑥1−𝛼⁄ ,𝑛−1 2 (𝑛 − 1)𝑠 2 (𝑛 − 1)𝑠 2 <𝜎<√ 2 √ 2 𝑥𝛼⁄ ,𝑛−1 𝑥1−𝛼⁄ ,𝑛−1 2 2 2 Hypothesis test about one variance 𝜎 2 1. 𝐻0 : 𝜎2 = 𝐻1 : 𝜎2 ≠ vs ≥ < ≤ > 2. Calculate the test statistic (T.S) 𝑥𝑐2 (𝑛 − 1)𝑆 2 = 𝜎2 3. Determine the rejection region 00 2 𝑥1− 𝛼⁄ 2,𝑛−1 𝑥𝛼2⁄ 2,𝑛−1 2 𝑥1−𝛼,𝑛−1 𝑥𝛼2 ,𝑛−1 4. Conclusion: Reject 𝐻0 if T.S 𝑥𝐶2 lies in rejection region Note: hypothesis test about one population st.dev(𝜎)is the same as hypothesis test about one population variance(𝜎 2 ), but you need to convert the hypothesis from 𝜎 to𝜎 2 . 21 Exercises: 1. A professor claims that the variance of the lengths of his lectures is within 2 square minutes. A random sample of 23 of these lectures was timed, and the variance of the lengths of these lectures was found to be 2.7 square minutes. Assume that the lengths of all such lectures by the professor are approximately normally distributed. a) Find the point estimate of the population variance b) Make the 98% confidence intervals for the variance and standard deviation of the lengths of all lectures by the professor. c) Test at the 1% significance level whether the variance of the lengths of all such lectures by the professor exceeds 2 square minutes. 22 2. An assembly line produces units with a mean weight of 10 and a standard deviation of 0.20. A new process supposedly will produce units with the same mean and a smaller standard deviation. A sample of 20 units produced by the new method has a sample standard deviation of 0.126. At a significance level of 10% can we conclude that the new process has less variation than the old? Review 1. Automotive part must be machined to close tolerances to be acceptable to customers. Production specifications call for a maximum variance in the lengths of the parts of 0.0004. Suppose the sample variance for 30 parts turns out to be 𝑠 2 = 0.0005. Using α=0.05, test to see whether the population variance specification is being violated. (𝑯𝟏 : 𝝈𝟐 > 𝟎. 𝟎𝟎𝟎𝟒, 𝒙𝟐𝒄 = 𝟑𝟔. 𝟐𝟓, 𝒙𝟐𝒕𝒂𝒃𝒍𝒆 = 𝟒𝟐. 𝟓𝟓𝟕, 𝒅𝒐 𝒏𝒐𝒕 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) 23 Chapter 10 I. The difference between two population means (𝝁𝟏 − 𝝁𝟐 ) for independent samples 𝜎1 & 𝜎2 unknown 𝜎1 & 𝜎2 known 𝑛1 & 𝑛2 Small 𝑛1 & 𝑛2 Large Point estimate: 𝜎12 ≠ 𝜎12 𝜎22 = 𝜎22 Point estimate: ̅𝑋1 − 𝑋̅2 (Homogenous) C.I: Point estimate: Point estimate: ̅𝑋1 − 𝑋̅2 C.I: 𝑆2 𝑆2 (𝑋̅1 − 𝑋̅2 ) ± 𝑍𝛼⁄ √ 1 + 2 2 𝑛 𝑛2 1 C.I: 𝑆12 𝑆22 + 𝑛1 𝑛2 (𝑋̅1 − 𝑋̅2 ) ± 𝑡𝛼⁄ ∗√ 2,𝑛 Test statistic : ( ̅𝑋1 − 𝑋̅2 ) − 𝐷 𝑡𝑐 = 𝑆2 𝑆2 √ 1+ 2 𝑛1 𝑛2 ̅𝑋1 − 𝑋̅2 2 𝑆2 𝑆2 ( 1 + 2) 𝑛1 𝑛2 2 2 𝑆2 𝑆2 ( 1) ( 2) 𝑛1 𝑛 + 2 𝑛1 − 1 𝑛2 − 1 𝑡𝑐 ~𝑡(𝑛∗ ) 1 1 + 𝑛1 𝑛2 . 𝑆𝑃. √ 2,𝑛1 +𝑛2 −2 Pooled estimate: (𝑛1 − 1)𝑆12 + (𝑛2 − 1)𝑆22 𝑆𝑃2 = 𝑛1 + 𝑛2 − 2 Test statistic : ( ̅𝑋1 − 𝑋̅2 ) − 𝐷 𝑡𝑐 = 1 1 𝑆𝑃√ + 𝑛1 𝑛2 Degree of freedom: 𝑛∗ = (𝑋̅1 − 𝑋̅2 ) ± 𝑡𝛼⁄ Test statistic : ( ̅𝑋1 − 𝑋̅2 ) − 𝐷 𝑍𝑐 = 𝑆2 𝑆2 √ 1+ 2 𝑛1 𝑛2 ̅𝑋1 − 𝑋̅2 C.I: 𝜎2 𝜎2 (𝑋̅1 − 𝑋̅2 ) ± 𝑍𝛼⁄ √ 1 + 2 2 𝑛 𝑛2 1 Test statistic : ( ̅𝑋1 − 𝑋̅2 ) − 𝐷 𝑍𝑐 = 𝜎2 𝜎2 √ 1+ 2 𝑛1 𝑛2 𝑍𝑐 ~𝑁(0,1) 𝑍𝑐 ~𝑁(0,1) 𝑡𝑐 ~𝑡(𝑛1 +𝑛2 −2) 24 II. 1. 𝐻0 : 𝜎21 = 𝜎22 Hypothesis test about Homogeneity (Equal population variances 𝜎12 = 𝜎22 ) 𝐻1 : 𝜎21 ≠ 𝜎22 vs 2. Calculate the test statistic (T.S) 𝐹𝐶 = 2 𝑆𝑙𝑎𝑟𝑔𝑒 2 𝑆𝑠𝑚𝑎𝑙𝑙 3. Determine the critical value 𝐹𝛼⁄2, 𝑛−1, 𝑛−1 Numerator Denominator 4. Conclusion: Reject 𝐻0 if T.S (𝐹𝐶 ) lies under the rejection region (under shaded area). 25 Exercises: 1. El-Mraay Dairy company claims that its 8-ounces low-fat yogurt cups contain on the average fewer calories than the 8-ounces low-fat yogurt cups produced by its competitor El-Safy company. In order to check this claim a sample of 50 such cups produced by El-Mraay showed that they contains on the average 144 calories per cup with a standard deviation of 5.4 calories. A sample of 40 cups of El-Safy product showed that they contain on the average 147 calories per cup with a standard deviation 6.3 calories. a. Make a 98% confidence interval for the difference between the mean number of calories in the 8-ounces low fat yogurt cups produced by the two companies b. Find the standard and margin error of part (a). c. Does your C.I obtained in part (a) support the hypothesis that the two means are different, what is the probability of type І error in that case. d. Test El-Mraay Dairy Company claim with α=0.05 26 2. Two brands (A and B) of tires are tested to compare their durability. The management of company claims that brand A is durable than brand B. Twelves from each brand are tested on a machine. The mileages (in hundreds of miles for each tire) have been recorded giving the following information. Mileages in hundreds Brand A 157 139 188 143 172 144 191 128 177 160 175 162 Brand B 160 118 150 165 158 159 127 133 170 164 152 142 Brand A Brand B Mean 161.3 149.8 Standard deviation 20.01 16.45 Assuming that two population are normally distributed a. At 5% level significance tests the hypothesis that the two populations are homogeneous (equal variances). b. Assuming homogeneous populations, test the management claim using α=0.05 27 3. A company claims that its medicine brand A provide faster relief from pain that another company’s medicine brand B. a researcher tested both brands of medicines on two groups of randomly selected patients. The results of the test are given in the following table. The mean and the standard deviation of relief time are in minutes. Brand Sample size Mean of relief time Standard deviation of relief time A 21 44 12.5 B 17 49 7.5 Assuming that relief time is normally distributed a. Assuming equal variances test the company claim at 0.05 level of significance b. Using α=0.05 test the hypothesis of homogeneous population (equal variances) 28 Review: 1. In order to study the performance of CBA students in Stat. 120. The QMIS department selected randomly 13 female and 12 male students and their final scores are recorded giving the following summary statistics Sample size Mean STD Female 13 84.15 9.90 male 12 76.58 11.27 Assuming that the scores have homogeneous normal distributions test the hypothesis that the female students scores on the average more than the male students (α=0.05). (𝑯𝟏 : 𝝁𝟏 > 𝝁𝟐 , 𝒕𝒄 = 𝟏. 𝟕𝟖𝟖, 𝒕.𝟎𝟓,𝟐𝟑 = 𝟏. 𝟕𝟏𝟒, 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) 2. A sample of 18 fathers who were company executives showed that they spend an average of 2.3 hours per week playing with their children, with a standard deviation of 0.54 hours. Another sample of 24 fathers who were medical professionals gave a mean of 4.6 hours per week with a standard deviation of 0.8 hours. Assume that the times spent per week playing with their children by all fathers who are executives and all fathers who are medical professional have normal distributions with equal standard deviations. a. Construct a 95% C.I for difference between the mean time spent per week playing with their children by all fathers who are executives and all fathers who are medical professionals. (-2.741, -1.858) b. Using the above C.I, test whether the mean time spent by all fathers who are executives is equal to that for all fathers who are medical professionals. (𝑯𝟏 : 𝝁𝟏 ≠ 𝝁𝟐 , 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) 3. A firm is studying the delivery times of two raw material suppliers. The firm is basically satisfied with supplier A and is prepared to stay with that supplier if the mean delivery time is the same as or less than that of supplier However, if the firm finds that the mean delivery time of supplier B is less than that of supplier A, it will begin making raw material from supplier B. a. What are the null and alternative hypotheses for this situation?(𝑯𝟏 : 𝝁𝑨 > 𝝁𝑩 ) b. Assume the independent samples show the following delivery time for the two suppliers: Supplier A Supplier B 𝑛1 =10 𝑛2 =20 𝑥̅1 =14 days 𝑥̅2 =12.5 days 𝑠1 =4 𝑠2 =2 With α=0.05 and using t-test with pooled variance what is your conclusion for the hypothesis from part (a)? What do you recommend in terms of supplier selection? (𝒕𝒄 = 𝟏. 𝟑𝟖, 𝒕.𝟎𝟓,𝟐𝟖 = 𝟏. 𝟕𝟎𝟏, 𝒅𝒐𝒏𝒐𝒕 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ). 29 4. In a random sample of nine gasoline stations in City “A”, the prices per gallon of unleaded gas have a standard deviation of $0.08 per gallon. In a random sample of 14 gasoline stations in city “B”, the prices per gallon have a standard deviation of $0.03 per gallon. Use the 10% significance level to test the null hypothesis that the price per gallon of gasoline is equally variable in two cities. (𝑯𝟏 : 𝝈𝟐𝟏 ≠ 𝝈𝟐𝟐 , 𝑭𝒄 = 𝟕. 𝟏𝟏, 𝑭𝟎.𝟎𝟓,𝟖,𝟏𝟑 = 𝟐. 𝟕𝟕, 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ). 5. On the basis of data provided by a salary survey, the variance in annual salaries for seniors in accounting firms is approximately 2.1 and the variance in annual salaries for managers in accounting firms is approximately 11.1. The salary data were provided in thousands of euros. Assuming the salary data were based on sample of 25 seniors and 26 managers, test the hypothesis that the population variances in the salaries are equal. At α=0.05, what is your conclusion? (𝑯𝟏 : 𝝈𝟐𝟏 ≠ 𝝈𝟐𝟐 , 𝑭𝒄 = 𝟓. 𝟐𝟗, 𝑭𝟎.𝟎𝟐𝟓,𝟐𝟓,𝟐𝟒 = 𝟐. 𝟐𝟔, 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ). 30 III. The difference between two population means (𝝁𝟏 − 𝝁𝟐 = 𝝁𝒅 ) for dependent (paired) samples Point estimate of (𝜇1 − 𝜇2 = 𝜇𝑑 ) 𝜇̂ 𝑑 = 𝑑̅ Confidence interval C.I 𝑆 𝑑̅ ± 𝑡𝛼⁄2,𝑛−1 𝑑 𝑖𝑓 𝜎 𝑢𝑛𝑘𝑛𝑜𝑤𝑛 𝑎𝑛𝑑 𝑛 < 30 √𝑛 Where d: difference between the two variables ∑𝑑 𝑑̅ = 𝑛 𝑆𝑑2 𝑆𝑑 = √𝑆𝑑2 = ∑ 𝑑2− (∑ 𝑑)2 𝑛 𝑛−1 or 𝑆𝑑2 = ∑ 𝑑2 −𝑛𝑑̅ 2 𝑛−1 or 𝑆𝑑2 = ∑(𝑑−𝑑̅)2 𝑛−1 Hypothesis test 𝑇𝑐 = 𝑑̅ −0 𝑆𝑑 √𝑛 𝑖𝑓 𝜎 𝑢𝑛𝑘𝑛𝑜𝑤𝑛 𝑎𝑛𝑑 𝑛 < 30 𝑇𝑐 ~𝑡𝑛−1 Note: We will use Z instead of T in both C.I and hypothesis test if o σ is known o σ is unknown with n≥30 there are three ways to do the test as mentioned in chapter 9 in this note 31 Exercises: 1. To test the difference between two body shop garages, 10 randomly chosen damaged cars were sent to these two garages (A and B). The following are the estimated repair garages of these garages. A 236 137 379 255 279 321 369 333 137 390 B 310 187 392 232 321 318 389 288 167 432 d=A-B 𝒅𝟐 Assuming that the repair charges are normally distributed a. Test the hypothesis that the repair charge at garage A is lower than that at garage B, state your assumptions. b. Construct a 95% C.I of the difference between the two means. 32 2. The manufacture of gasoline additive claims that the use of this additive increases gasoline mileage. A random sample of 6 cars were driven for one week with the gasoline additive and then for one week without the gasoline additive. The following table provides the obtained information about the gasoline mileage. Gasoline mileage With without D=with-without Mean 25.12 23.4 1.717 Standard deviation 5.87 5.42 1.427 a. Compute a 99% confidence interval for the mean difference gasoline mileage? b. Is it possible to say that the manufacturer’s claim is true? Why? Use α=0.01 33 Review: 1. A company claims that its 12-week special exercise program significantly reduces weight. A random sample of six persons was selected, and these persons were put on this exercise program for 12 weeks. The following table gives the weights (in pounds) of those six persons before and after the program. Assume that the population of all paired differences is (approximately) normally distributed. Before After 180 183 195 187 177 161 221 204 208 197 199 189 a. Make a 95% confidence interval for the mean of the population paired differences, where a paired difference is equal to the weight before joining this exercise program minus the weight at the end of the 12-week program. (2.278, 17.382) b. Using the 1% significance level, can you conclude that the mean weight loss for all persons due to this special exercise program is greater than zero?(𝑯𝟏 : 𝝁𝒅 > 𝟎, 𝒕𝒄 = 𝟑. 𝟑𝟓, 𝒕.𝟎𝟏,𝟓 = 𝟑. 𝟑𝟔𝟓, 𝒅𝒐𝒏𝒐𝒕 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) 2. A study used to test whether a training course is helpful for students to pass a mathematics course. To evaluate the effectiveness of the training course, eight students test scores were compared before and after taking the training course. The results are as follows Scores student before after 1 46 50 2 52 50 3 64 71 4 67 70 5 58 54 6 55 61 7 60 62 8 60 68 a. Compute a 90% confidence interval for the mean difference scores? (0.25, 5.75) b. Is it possible to say that the training course is helpful? Why? (𝑯𝟏 : 𝝁𝒅 > 𝟎, 𝒕𝒄 = 𝟐. 𝟎𝟔, 𝒕.𝟎𝟓,𝟕 = 𝟏. 𝟖𝟗𝟓) 3. A company is considering installing new machines to assemble its products. The company is considering two types of machines, but it will buy only one type. The company selected 11 assembly workers and asked them to use these two types of machines to assemble products. The time in minutes to assemble one unit of the product on each type of machine for each of these eleven workers is recorded and given to company statistician who supplied the following information Machine І 23 26 19 24 27 22 20 18 17 21 25 Machine П 21 24 23 25 24 28 24 21 17 26 23 Assuming normality, use a confidence interval for the difference between the average assembly time for the two machines to test the hypothesis that the two machines are the same at α=0.05. (𝑯𝟏 : 𝝁𝒅 ≠ 𝟎, (−𝟑. 𝟒𝟔𝟐, 𝟎. 𝟗𝟏𝟔), 𝒅𝒐𝒏𝒐𝒕 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) 34 IV. The difference between two population proportions (𝑷𝟏 − 𝑷𝟐 ) 𝑃̂1 − 𝑃̂2 Point estimate of 𝑃1 − 𝑃2 Confidence interval C.I (𝑃̂1 − 𝑃̂2 ) ± 𝑍𝛼⁄2 √ 𝑃̂1 (1 − 𝑃̂1 ) 𝑃̂2 (1 − 𝑃̂2 ) + 𝑛1 𝑛2 Hypothesis test 𝑍𝑐 = (𝑃̂1 − 𝑃̂2 ) − 𝐷 1 1 √𝑃̅ (1 − 𝑃̅) ( + ) 𝑛1 𝑛2 Where Combined sample proportion 𝑋 +𝑋 𝑃̅ = 𝑛1 +𝑛2 1 2 or ̂ ̂ 𝑛 𝑃 +𝑛 𝑃 𝑃̅ = 1𝑛1+𝑛2 2 1 2 35 Exercises: 1. A company has two restaurants in two different areas in Kuwait. The company wants to estimate the percentage of customers who thinks that the food and service at each of these restaurants are excellent. A sample of 200 customers taken from restaurant in area A showed that 118 think that the food and service are excellent in this restaurant. Another sample of 250 customers taken from restaurant in area B showed that 160 think that the food and service are excellent in this restaurant. a. Find the point estimate of the difference between the two proportions. b. Construct a 97% C.I of the difference between the two proportions. c. Find the p-value to test the hypothesis that the proportion of customers who thinks that the food and service in area A is lower than the corresponding proportion at the restaurant in area B. d. What is your conclusion if α=0.025? 36 Review: 1. In a random sample of 800 men aged between 25 to 35, 24% of them said they live with one parent. In other sample of 850 women of the same age group, 18% said that they live with one parent. Construct a 95% confidence interval for the difference between the two population proportions. (0.021, 0.099) 2. A company that has many department stores wanted to find at two such stores the percentage of sales for which at least one of the items was returned. A sample of 800 sales randomly selected from store A showed that for 240 of them at least one of the items was returned. Another sample of 900 sales randomly selected from store B showed that for 279 of them at least one of the items was returned. a. Construct at 98% confidence interval for the difference between the proportions of all sales at the two stores for which at least one of the items was returned. (-0.0621, 0.0421) b. Find the standard error and the margin error of C.I. (0.02236,0.05211) c. Using the 1% significance level, can you conclude that at the two stores the proportions of all sales for which at least one of the items was returned are different?(𝑯𝟏 : 𝑷𝑨 ≠ 𝑷𝑩 , 𝒁𝒄 = −. 𝟒𝟓, 𝒅𝒐𝒏𝒐𝒕 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) d. Find the p-value for the test mentioned in part (c). (0.6528) e. Find the standard error of the test. (0.02237) 37 Chapter 11 ANOVA Assumptions: 1. “k” random independent samples from 2. Normal population with 3. Equal variances (homogenous populations) Hypothesis test: 1. 𝐻0 : 𝜇1 = 𝜇2 = ⋯ = 𝜇𝑘 vs 𝐻1 : at least one population means is different Where k: # of samples or groups or populations 2. T.S 𝐹𝑐 = 3. 𝑀𝑆𝐵 (𝑀𝑆𝐹) 𝑀𝑆𝑊 (𝑀𝑆𝐸) Calculated from ANOVA table Determine the Critical value 𝐹𝛼,𝑘−1,𝑛−𝑘 4. Conclusion: Reject 𝐻0 if T.S (𝐹𝑐 ) lies in the rejection region R.R (under shaded area). 38 Source of variation Between (Factor) Degrees of freedom (d.f) k-1 Sum of squares (SS) SSB (SSF) Within (Error) n-k SSW (SSE) Total n-1 SST SSW(SSE) 𝑇12 SSW(SSE) n−k Fc = MSB(MSF) MSW(MSE) - 𝑇22 𝑇1 = 𝑛1 𝑥̅1 , 𝑇𝑘2 𝑇2 = 𝑛2 𝑥̅ 2 , … , 𝑇𝑘 = 𝑛𝑘 𝑥̅𝑘 𝑇2 SSB = SST-SSW SSB = MSB (k-1) SSB = ( SSW = SST-SSB SSW = (𝑛1 − 1)𝑆12 + (𝑛2 − 1)𝑆22 + ⋯ + (𝑛𝑘 − 1)𝑆𝑘2 = ∑(𝑛𝑖 − 1)𝑆𝑖2 SST = SSB+SSW 𝑀𝑆𝐸 ∗ = 𝑆𝑃2 = 𝑛1 + 𝑛2 + ⋯+ SSB = ∑ 𝑛𝑖 (𝑥̅𝑖 − 𝑥̅ )2 SSW = MSW (n-k) SST MSW(MSE) = k: number of samples/ groups/ populations. 𝑛 = 𝑛1 + 𝑛2 + ⋯ + 𝑛𝑘 (𝑡𝑜𝑡𝑎𝑙 𝑠𝑎𝑚𝑝𝑙𝑒 𝑠𝑖𝑧𝑒). 𝑇1 = ∑ 𝑥1 , 𝑇2 = ∑ 𝑥2 , … , 𝑇𝑘 = ∑ 𝑥𝑘 𝑜𝑟 𝑇 = 𝑇1 + 𝑇2 + ⋯ + 𝑇𝑘 𝑆12 , 𝑆22 , … , 𝑆𝑘2 ∑ 𝑥 2 = ∑ 𝑥12 + ∑ 𝑥22 + ⋯ + ∑ 𝑥𝑘2 SSB(SSF) Mean squares (MS) SSB(SSF) MSB(MSF) = k−1 𝑛𝑘 )− 𝑇2 𝑇2 𝑇2 1 2 𝑘 𝑛 SSW=∑ 𝑥 2 − (𝑛1 + 𝑛2 + ⋯ + 𝑛𝑘 ) SST =∑ 𝑥 2 − 𝑇2 𝑛 (𝑛1 − 1)𝑆12 + (𝑛2 − 1)𝑆22 + ⋯ + (𝑛𝑘 − 1)𝑆𝑘2 𝑛−𝑘 Note: ∑ 𝒙𝟐 ≠ (∑ 𝒙)𝟐 𝑻𝒊 𝟐 ≠ ∑ 𝒙𝟐𝒊 𝑻𝒊 𝟐 = (∑ 𝒙𝒊 )𝟐 39 Exercise 1. A consumer agency wanted to find out if the mean time it takes for each of three brands of medicine to provide relief from a headache is the same. The three drugs were administered to three randomly selected samples. The following table gives the time in minutes taken by each patient to get relief from a headache, followed by a Minitab output to such problem. Drug П 14 20 18 24 І 25 38 42 65 47 52 Level Drug І Drug П Drug Ш N 6 4 5 Mean 44.83 19.00 53.60 StDev 13.50 4.16 13.24 Ш 44 39 54 58 73 Individual 95% CIs for Mean Based on Pooled StDev -------+---------+---------+--------(------*------) (-------*-------) (-------*------) -------+---------+---------+--------16 32 48 a. Complete the analysis of variance table Source Factor Error Total df SS MS F b. Test the consumer agency claim at 5% level of significance c. Suppose that the hypothesis of equal means has been rejected which of the drugs is different and why? 40 2. A panel of trained testers judges the flavor quality of different vanilla frozen desserts: frozen yogurts, ice milks, other frozen desserts measured on a scale from 0 to 100. The sample sizes are respectively, 𝑛1 = 13, 𝑛2 = 8, 𝑎𝑛𝑑 𝑛3 = 6. Below is most of the ANOVA output from the computer: Source Factor (Between) Error (Within) Total df ? SS 6364 MS 3182 24 3031 ? ? ? F ? a. Complete the ANOVA table b. Test whether there is a significant difference in the flavor quality of the three different disserts State the null and alternative hypotheses Find the value of the test statistic Find the critical value(s). use 0.05 significance level What is your conclusion about the flavor quality of the three different disserts? What are the assumptions required to make this test? 41 3. Sex hours were selected from each of 3 radio stations, and analysis of variance was performed on the data. Part of the ANOVA table is shown below Source Between Within Total df SS MS 1311.02 F 13.368 a. Complete ANOVA table b. At 0.05 significance level, is there a difference in the stations means 42 Review: 1. A statistics professor has developed four methods (M1, M2, M3, M4) for teaching a senior level class. He wishes to investigate if there is a difference in the four methods. The professor assigns students to the four teaching methods. The final exam scores for each group were recorded. The four sample sizes and sample means are in the following table: Method Sample size Sample mean M1 7 79 M2 4 83.75 M3 6 70 M4 5 72.8 Also you are given that the error (within) sum of squares ”SSE” (SSW)=861.55 Carry out ANOVA test using a 1% level of significance State the null and alternative hypotheses Find the value of test statistic (3.973) Find the critical value (5.09) What is your conclusion about the four different methods of teaching? (don’t reject 𝑯𝟎 ). Source Between Within Total df 3 18 21 SS 570.45 861.55 1432 MS 190.15 47.864 F 3.973 2. Samples were selected from three populations, the data obtained is given below Sample 1 Sample 2 Sample 3 91 77 88 98 87 75 107 84 73 102 95 84 85 75 82 a. State the assumption needed to use the analysis of variance to test the equality of the three population means b. Test the hypothesis of no difference between the three population means at 0.05 level of significance.(𝑭𝒄 = 𝟏𝟏. 𝟖𝟖𝟓, 𝑭.𝟎𝟓,𝟐,𝟏𝟐 = 𝟒. 𝟒𝟔, 𝒓𝒆𝒋𝒆𝒄𝒕 𝑯𝟎 ) Source Between Within Total df 2 12 14 SS 968.7 489 1457.7 MS 484.35 40.75 F 11.885 43 Chapter 12 Independence 1. 𝐻0 : two variables are independent (𝐧𝐨𝐭 𝐫𝐞𝐥𝐚𝐭𝐞𝐝) vs 𝐻1 : two variables are dependent (𝐫𝐞𝐥𝐚𝐭𝐞𝐝) 2. Calculate the test statistic (T.S) 𝑥𝑐2 = ∑ (𝑂 − 𝐸)2 𝐸 Where O: Observed value E: Expected value E= row total ∗ column total total 3. Determine the critical value 2 𝑥𝛼,(𝑟−1)(𝑐−1) 4. Conclusion: Reject 𝐻0 if T.S (𝑥𝑐2 ) lies in the rejection region (under shaded area). 44 Exercises: 1. Let's try an example. 500 elementary school boys and girls are asked which is their favorite color: blue, green, or pink? Results are shown below: Boys Girls Total Blue 100 20 120 Green 150 30 180 Pink 20 180 200 Total 300 200 500 would you conclude that there is a relationship between gender and favorite color? a. The two hypothesis 𝐻0 : 𝑣𝑠 𝐻1 : b. The test statistic c. The critical value(s). Use 0.05 significance level. d. The conclusion 45 2. One hundred auto drivers who were stopped by police for some violation were also checked to see if they were wearing seat belt. The following table records the results of this survey Wearing seat belt Not wearing seat belt Total Men 34 21 55 Women 32 13 45 total 66 34 100 For a chi square test of independence for this contingency table: a. What is the number of degrees of freedom? b. What is the total of the second row? c. How many drivers are in the sample ? d. What are the observed frequencies for the first row? e. What are the expected frequencies for the second row? f. What are the observed frequencies for the second column? g. What are the expected frequencies for the second column? 46 CHAPTER 13 Simple Linear Regression I. The population regression model 𝑦 = 𝛽0 + 𝛽1 𝑥 + 𝜀 Where o o o o o 𝑦: is the dependent variable 𝑥: is the independent variable 𝛽0: is y-intersection or constant term 𝛽1: is the slope 𝜀: is a random error term Estimate the population regression model by the sample linear regression model 𝑦̂ = 𝑏0 + 𝑏1 𝑥 This equation is called the least squares regression line or the prediction equation. Sum of squares 𝑆𝑆𝑥𝑦 = ∑ 𝑥𝑦 − ∑𝑥∑𝑦 𝒐𝒓 𝑆𝑆𝑥𝑦 = ∑ 𝑥𝑦 − 𝑛𝑥̅ 𝑦̅ 𝒐𝒓 𝑆𝑆𝑥𝑦 = ∑(𝑥 − 𝑥̅ )(𝑦 − 𝑦̅) 𝑛 𝑆𝑆𝑥𝑥 (∑ 𝑥)2 = ∑𝑥 − 𝒐𝒓 𝑆𝑆𝑥𝑥 = ∑ 𝑥 2 − 𝑛𝑥̅ 2 𝒐𝒓 𝑆𝑆𝑥𝑥 = ∑(𝑥 − 𝑥̅ )2 𝑛 𝑆𝑆𝑦𝑦 (∑ 𝑦)2 = ∑𝑦 − 𝒐𝒓 𝑆𝑆𝑦𝑦 = ∑ 𝑦 2 − 𝑛𝑦̅ 2 𝒐𝒓 𝑆𝑆𝑦𝑦 = ∑(𝑦 − 𝑦̅)2 𝑛 2 2 Estimated value of 𝛽0 and 𝛽1 𝑆𝑆𝑥𝑦 𝑆𝑆𝑥𝑥 ̂ 𝐵0 = 𝑏0 = 𝑦̅ − 𝑏1 𝑥̅ 𝐵̂1 = 𝑏1 = Prediction value of y 𝑦̂ = 𝑏0 + 𝑏1 𝑥 given Residual (Error) 𝑒 = 𝑦 − 𝑦̂ given 47 II. How to Evaluate the estimated model 1. Coefficient of Determination 𝑟2 = 𝑏1 𝑆𝑆𝑥𝑦 𝑆𝑆𝑅 = 𝑆𝑆𝑦𝑦 𝑆𝑆𝑇 0 ≤ 𝑟2 ≤ 1 It explains the variation in “y” by the independent variable “x” 𝑟 2 increased Note: SSR increased Good model 2. Coefficient of Correlation 𝑟 = √𝑟 2 or 𝑟= (with the same sign of 𝑏1 ) 𝑆𝑆𝑥𝑦 √𝑆𝑆𝑥𝑥 𝑆𝑆𝑦𝑦 = 𝑏1 √ 𝑆𝑆𝑥𝑥 𝑆𝑆𝑦𝑦 −1 ≤ 𝑟 ≤ 1 It measures the strength of the linear relationship between two variables Perfect Perfect III. Estimation of the variance and standard deviation of random errors The estimated variance of errors 𝜎̂𝜖2 = 𝑆𝑒2 = 𝑀𝑆𝐸 The estimated St. Deviation of errors 𝜎̂𝜖 = 𝑆𝑒 = √𝑀𝑆𝐸 𝑴𝑺𝑬 = 𝑺𝑺𝒚𝒚 − 𝒃𝟏 𝑺𝑺𝒙𝒚 𝑺𝑺𝑬 = 𝒏−𝒌 𝒏−𝒌 (k: number of parameters) 48 IV. Inferences about 𝜷𝟏 𝒃𝟏 ~𝑵(𝝁𝒃𝟏 = 𝑩𝟏 , 𝑺𝒃𝟏 = 𝑺𝒆 √𝑺𝑺𝒙𝒙 Population simple linear regression equation 𝑦 = 𝛽0 + 𝛽1 𝑥 + 𝜀 Point estimate of 𝛽1: 𝛽̂1 = 𝑏1 Confidence interval of 𝛽1 o If 𝑛 < 30 Hypothesis test about 𝐵1 𝑏1 ± 𝑡𝛼⁄2,𝑛−𝑘 𝑆𝑏1 ) (k: number of parameters) (Test of 𝑏1 or Test if there is a good relationship between x and y). 1. 𝑯𝟎 : 𝜷 𝟏 = 𝟎 Means there is no relationship between X and Y (not significant linear relationship) (X will dropped from model) 𝑯𝟏 : 𝜷 𝟏 ≠ 𝟎 Means there is a relationship between X and Y (significant linear relationship) 𝑯𝟏 : 𝜷 𝟏 > 𝟎 Positive linear relationship 𝑯𝟏 : 𝜷 𝟏 < 𝟎 negative linear relationship 2.Calculate Test statistic 𝑏 𝑇𝑐 = 𝑆 1 o If 𝑛 < 30 𝑏1 3.Determine the rejection region −𝑡𝛼⁄2,𝑛−𝑘 𝑡𝛼⁄2,𝑛−𝑘 −𝑡𝛼,𝑛−𝑘 𝑡𝛼,𝑛−𝑘 4.Conclusion: Reject 𝐻0 if T.S lies in rejection region (R.R) 49 V. Testing the overall model 1. 𝐻0 : 𝛽1 = 0 The model is not significant/ not useful/not good/not adequate /data not fit model. 𝐻1 : 𝛽1 ≠ 0 The model is significant/ useful/ good/adequate/data fit model 2. Test statistic 𝑀𝑆𝑅 𝐹𝑐 = 𝑀𝑆𝐸 (Calculated from ANOVA table) 3. Critical value 𝐹𝛼,𝑘−1,𝑛−𝑘 4. Conclusion Reject 𝐻0 if T.S (𝐹𝑐 ) lies in the rejection region R.R (under shaded area). ANOVA table Source of variation Regression Residual Error Total d.f Sum of squares SS Mean squares MS k-1 𝑆𝑆𝑅 = 𝑏1 𝑆𝑆𝑥𝑦 n-k 𝑆𝑆𝐸 = 𝑆𝑆𝑇 − 𝑆𝑆𝑅 𝑆𝑆𝑅 𝑘−1 𝑆𝑆𝐸 𝑀𝑆𝐸 = 𝑛−𝑘 n-1 𝑆𝑆𝑇 = 𝑆𝑆𝑦𝑦 𝑀𝑆𝑅 = T.S 𝐹𝑐 = 𝑀𝑆𝑅 𝑀𝑆𝐸 𝒌 = # 𝒐𝒇 𝒑𝒂𝒓𝒂𝒎𝒆𝒕𝒆𝒓𝒔 50 CHAPTER 14 Multiple Regressions I. Least squares regression line equation 𝑦̂ = 𝑏0 + 𝑏1 𝑥1 + 𝑏2 𝑥2 + 𝑏3 𝑥3 + ⋯ 𝑦̂: Dependent variable (prediction of y) 𝑥𝑖 : Independent variable II. Hypothesis test 1. 𝐻0 : 𝛽1 = 𝛽2 = 𝛽3 = ⋯ = 0 (the model is not significant) Vs 𝐻1 : at least one β is not equal to zero (the model is significant) 2. Test statistic 𝑀𝑆𝑅 𝐹𝑐 = 𝑀𝑆𝐸 (Calculated from ANOVA table) 3. Critical value 𝐹𝛼,𝑘−1,𝑛−𝑘 4. Conclusion Reject 𝐻0 if T.S (𝐹𝑐 ) lies in the rejection region R.R (under shaded area). ANOVA table Source of d.f variation Regression k-1 Residual Error Total Sum of squares SS Mean squares MS 𝑆𝑆𝑅 = 𝑏1 𝑆𝑆𝑥𝑦 𝑆𝑆𝑅 𝑘−1 𝑆𝑆𝐸 𝑀𝑆𝐸 = 𝑛−𝑘 n-k 𝑆𝑆𝐸 = 𝑆𝑆𝑇 − 𝑆𝑆𝑅 n-1 𝑆𝑆𝑇 = 𝑆𝑆𝑦𝑦 𝑀𝑆𝑅 = T.S 𝐹𝑐 = 𝑀𝑆𝑅 𝑀𝑆𝐸 51 Exercises: 1. The following table gives information on the temperature in a city and the volume of ice cream (in pounds) sold at an ice cream parlor for a random sample of eight days during the summer of 1999. Temperature 93 86 77 89 98 102 87 79 Ice cream sold 208 175 123 198 232 277 158 117 ∑𝑥 = 711 , ∑𝑦 = 1488, ∑𝑥 2 = 63713, ∑𝑦 2 = 297428, ∑𝑥𝑦 = 135466, 𝑥̅ = 88.88, 𝑦̅ = 186 a. Find sum of squares (SS) b. Find the least squares regression line (𝑦̂ = 𝑎 + 𝑏𝑥) c. Give a brief interpretation of the values of a and b - a(𝑏0 ): the initial value of y when x=0 (the initial value of the volume of ice-cream sold (y) is equal to a= -361.5008 when the temperature (x)is equal to zero) - b(𝑏1 ): if we increase x by 1 unit then y will change (increase or decrease) by the value of b. (if we increase the temperature (x) by 1 degree then the volume of ice-cream sold (y) will increase by b=6.16. d. Compute 𝑟 and 𝑟 2 , explain what they mean e. Predict the amount of ice cream sold on a day with a temperature of 95° f. Compute the standard deviation of errors g. Construct a 99% confidence interval for 𝛽1 h. Testing at 1% significance level, can you conclude that 𝛽1 is different from zero? 52 2. Regression analysis was applied between sales data (in $1000) and advertising data (in $100) and the following information was obtained 𝑦̂ = 12 + 1.8𝑥 𝑛 = 17, 𝑆𝑆𝑅 = 225, 𝑆𝑆𝐸 = 75, 𝑆𝑏1 = 0.2683 a. Based on the above estimated regression equation, if advertising is $3000, then the predicted value of sales (in dollars) is b. The F statistic computed from the above data is c. The critical F value at α=0.05 is d. Is the estimated regression model significant? The two hypotheses Your conclusion e. The t statistic for testing the significance of the slope is f. Is the linear relationship between X and Y significant? Use the t-test to answer this equation. The two hypotheses The critical value(s) Your conclusion g. Calculate the 95% confidence interval of the slope of the regression line for all statistics students h. Develop an analysis of variance table Source of d.f SS variation MS 53 3. The owner of a bowling establishment is interested in the relationship between the price she charges for a game of bowling and the number of games bowled per day. She collected data on the number of games bowled per day at 15 different prices. Fill in the missing entries in the following MINITAB output that was obtained for these data. In this output, X represents the price of a game and Y is the number of games bowled per day. The regression equation is y = ____ ____ x Predictor Constant x Coef 691.02 -141.30 S = _____ STDEV 21.70 ____ R-Sq = _____ T ____ -16.83 P 0.000 0.000 R-Sq(adj) = 95.3% Analysis of Variance Source Regression Residual Error Total DF ___ ___ ___ SS 148484.0 _______ _______ MS _______ _______ F 283.13 P 0.000 4. A researcher wanted to examine the relation between a dependent variable y and an independent variable x, He selected randomly 10 observations giving the following partial MINITAB output: A. Predictor Constant X1 S = 15.2158 Coef 247.97 -8.172 SE Coef 15.01 1.077 R-Sq = 87.8% R-Sq(adj) = 86.3% 1. Write down the estimated regression equation: 2. Test the hypothesis of no regression (𝑏1 =0) using α=0.05 3. Find the correlation coefficient between y and x1 and comment on its value 54 B. To researcher decided to add another independent variable x2 to the model in (A) he obtained the following results The regression equation is y = 180 - 6.17 x1 + 0.848 x2 Predictor Constant X1 X2 S = 10.2957 Coef 180.07 ______ 0.8484 SE Coef 23.31 ______ 0.2622 R-Sq = _______ T _____ -6.46 _____ R-Sq(adj) = 93.7% Analysis of Variance Source Regression Residual Error Total DF 2 _ 9 SS ______ 742.0 15182.9 MS _______ _______ F _____ 1. Complete the missing values in the previous MINITAB output 2. Test at α=0.05 of no regression model (i.e. the overall model does not fit the data). 3. Find a 95% confidence interval for the regression coefficient of x2 4. Test the hypothesis that the true value of the regression coefficient of x1 equal to 0 5. Which of the two models you prefer, the one estimated in (A) above or the one estimated in (B) above? And why? 6. Test the hypothesis that the true value of the regression coefficient of 𝑥2 is positive (α=.05). 55 Inference about 𝜷𝒊 The regression equation is y = 180 - 6.17 x1 + 0.848 x2 𝑏0 𝑏1 Predictor Constant 𝑏2 Coef SE Coef 𝑏0 180.07 X1 𝑏1 -6.17 X2 𝑏2 T 𝑆𝑏0 23.31 7.725 𝑆𝑏2 0.2622 S = 10.2957 R-Sq = 0.9511 Estimated standard deviation of error Coefficient of determination √𝑀𝑆𝐸 𝑆𝑆𝑅 𝑆𝑆𝑇 0.00 𝑏𝑖 -6.46 𝑆𝑏𝑖 𝑆𝑏1 0.955 0.8484 p-value 0.00 3.236 0.00 Testing hypothesis for two tailed test we compare p-value with α. The significant of 𝛽𝑖 or the linear relationship between 𝑥𝑖 𝑎𝑛𝑑 𝑦𝑖 R-Sq(adj) = 93.7% Over all model (conduct the f test of model usefulness/test the whole model/ 𝑯𝟎 : 𝜷𝟏 = 𝜷𝟐 = 𝟎 𝒗𝒔 𝑯𝟏 : 𝒂𝒕 𝒍𝒆𝒂𝒔𝒕 𝒐𝒏𝒆 𝜷 ≠ 𝟎) Analysis of Variance Source DF SS Regression 2 14440.9 Residual Error 7 742.0 Total 9 15182.9 MS F 7220.45 68.117 106 Error mean square 𝑀𝑆𝐸 = Or 𝑆𝑆𝐸 𝑛−𝑘 𝑀𝑆𝐸 = 𝑆 2 56 5. The wner of ShowTime Movie theaters would like to estimate weekly gross revenue as a function of advertising expenditure. Historical data for a sample of 8 weeks follow Weekly gross Revenue (Y) Television advertising (X1) Newspaper advertising (X2) ($1000s) ($1000s) ($1000s) 96 5.0 1.5 90 2.0 2.0 95 4.0 1.5 92 2.5 2.5 95 3.0 3.3 94 3.5 2.3 94 2.5 4.2 94 3.0 2.5 A portion of the MINITAB computer follows The regression equation is y = 83.2 + 2.29 x1 + 1.30 x2 Predictor Constant X1 X2 S = 0.642587 Coef SE Coef 1.574 0.3041 0.3207 T R-Sq = 91.9% Analysis of Variance Source Regression Residual Error Total DF SS 23.435 MS F 5 a. What is the estimate of the weekly gross revenue for a week when $3500 is spent on television advertising and $1800 is spent on newspaper advertising? 57 b. Find and interpret 𝑅 2 c. When television advertising was the only independent variable, 𝑅 2 =0.653 (65.3%) do you prefer the multiple regression results? Why? d. Use α=0.05 to test the hypotheses 𝐻0 : 𝛽1 = 𝛽2 = 0, 𝐻1 : 𝛽1 𝑎𝑛𝑑/𝑜𝑟 𝛽2 is not equal to zero. Did the estimated regression equation provide a good fit to the data? Explain e. Find the mean square error. Find the standard error of the estimate (𝜎̂) f. Use α=0.05 to test the significance of each independent variable. Should X1 or X2 be dropped from the model 58 TABLES 59 60 61 62 63 64 65 66 67 68 69 70