Download Document

Lecture 1.7.
AM FM PM
OOK BPSK FSK
AM, FM, and Digital Modulated Systems





Amplitude Modulation (AM)
Double Sideband Suppressed carrier (DSSC)
Assymetric Sideband Signals
Single sideband signals (SSB)
Frequency Division Multiplexing (FDM)
Bandpass Signaling Review
 The modulated bandpass signal can be described by
s(t )  Re{ g (t )e j C t }
Where
c  2f c ;
m(t) →g(t)
Modulation Mapping function: Convert
V( f ) 
 The voltage spectrum of the bandpass signal is
The PSD of the bandpass signal is
Where G f   F g t ;
Pv ( f ) 
f c - Carier Frequency

Ref : Table 4-1


1
G  f  f c   G *  f  f c 
2

1
Pg  f  f c   Pg  f  f c 
4
Pg  f  - PSD of the complex envelope g(t);
Amplitude Modulation
 The Complex Envelope of an AM signal is given by
g (t )  Ac [1  m(t )]
Ac indicates the power level of AM and m(t) is the Modulating Signal
 Representation of an AM signal is given by
s(t )  Ac [1  m(t )]cos ct
 Ac[1+m(t)]
In-phase component x(t)
 If m(t) has a peak positive values of +1 and a peak negative value of -1
AM signal  100% modulated
 Envelope detection can be used if % modulation is less than 100%.
Amplitude Modulation
An Example of a message signal m(t)
Waveform for Amplitude modulation of the message signal m(t)
Amplitude Modulation
B
An Example of message energy spectral density.
Carrier component together
with the message
2B
Energy spectrum of the AM modulated message signal.
AM – Percentage Modulation
 Definition: The percentage of positive modulation on an AM signal is
% Positive Modulation 
Amax  Ac
100  max  m(t )  100
Ac
 The percentage of negative modulation on an AM signal is
Ac  Amin
100   min  m(t )  100
Ac
 The percentage of overall modulation is
max  m(t )  min  m(t ) 
Amax  Amin
% Modulation 
100 
100
2 Ac
2
Amax - Maximum value of Ac [1  m(t )]
Amin - Minimum value of Ac [1  m(t )]
Ac - Level of AM envelope in the absence of modulation [i.e., m(t)  0]
If m(t) has a peak positive values of +1 and a peak negative value of -1
AM signal  100% modulated
AM Signal Waveform
Amax = 1.5Ac
Amin = 0.5 Ac
% Positive modulation= 50%
% Negative modulation =50%
Overall Modulation = 50%
AM – Percentage Modulation
Under modulated (<100%)
100% modulated
Over Modulated (>100%)
Envelope Detector
Envelope Detector
Can be used
Gives Distorted signal
AM – Normalized Average Power
The normalized average power of the AM signal is
1
1
2
2
g t   Ac2 1  mt 
2
2
1
 Ac2 1  2mt   m 2 t 
2
1
1
 Ac2  Ac2 mt   Ac2 m 2 t 
2
2
s 2 t  


If the modulation contains no dc level, then mt   0
The normalized power of the AM signal is
s 2 t  
1 2
1 2 2
Ac 
Ac m t 
2
2
Discrete Carrier Power
Sideband power
AM – Modulation Efficiency
 Definition : The Modulation Efficiency is the percentage of the total power
of the modulated signal that conveys information.
Only “Sideband Components” – Convey information
Modulation Efficiency:
E
m2  t 
1  m t 
2
100
Highest efficiency for a 100% AM signal : 50% - square wave modulation
Normalized Peak Envelope Power (PEP) of the AM signal:
PPEP
Ac2
1  max mt 2

2
Voltage Spectrum of the AM signal:
Ac
  f  f c   M  f  f c     f  f c   M  f  f c 
S( f ) 
2
Unmodulated Carrier
Spectral Component
Translated Message Signal
Example 5-1. Power of an AM signal
Suppose that a 5000-W AM transmitter is connected to a 50 ohm load;
Then the constant Ac is given by
1 Ac2
 5,000  Ac  707 V
2 50
Without
Modulation
If the transmitter is then 100% modulated by a 1000-Hz test tone ,
the total (carrier + sideband) average power will be
 1  Ac2 
  1.5  5000   7,500W
1.5 

2
50
 

1
 2

 m t   2 for 100% modulation 
The peak voltage (100% modulation) is (2)(707) = 1414 V across the 50 ohm load.
The peak envelope power (PEP) is
 1  Ac2 
  4   5000   20,000W
4  

2
50
 

The modulation efficiency would be 33% since < m2(t) >=1/2
Double Side Band Suppressed Carrier (DSBSC)
• Power in a AM signal is given
by
s 2 t  
1 2
1 2 2
Ac 
Ac m t 
2
2
Carrier Power
 DSBSC is obtained by eliminating carrier component
If m(t) is assumed to have a zero DC level, then
Spectrum  S ( f ) 
Sideband power
s(t )  Ac m(t ) cos ct
Ac
M  f  f c   M  f  f c 
2
1 2 2
Power 
s t  
Ac m t 
2
m 2 t 
Modulation Efficiency 
E 2
100  100%
m t 
2
Disadvantages of DSBSC:
• Less information about the carrier will be delivered to the receiver.
• Needs a coherent carrier detector at receiver
DSBSC Modulation
s(t )  Ac m(t ) cos ct
B
An Example of message energy spectral density.
No Extra Carrier
component
2B
Energy spectrum of the DSBSC modulated message signal.
Carrier Recovery for DSBSC Demodulation
 Coherent reference for product detection of DSBSC can not be obtained by the
use of ordinary PLL because there are no spectral line components at fc.
Carrier Recovery for DSBSC Demodulation
 A squaring loop can also be used to obtain coherent reference carrier for product
detection of DSBSC. A frequency divider is needed to bring the double carrier
frequency to fc.
Single Sideband (SSB) Modulation
 An upper single sideband (USSB) signal has a zero-valued spectrum for
 A lower single sideband (LSSB) signal has a zero-valued spectrum for
 SSB-AM – popular method ~ BW is same as that of the modulating signal.
Note: Normally SSB refers to SSB-AM type of signal
USSB
LSSB
f  fc
f  fc
Single Sideband Signal
 Theorem : A SSB signal has Complex Envelope and bandpass form as:
ˆ t 
g t   Ac mt   jm
ˆ (t ) sin ct 
st   Ac mt  cos ct  m
mˆ (t ) – Hilbert transform of m(t)  m
ˆ t   mt   ht 
H  f   ht 
 j ,
H f   
 j,
Hilbert Transform corresponds to a -900 phase shift
and
H(f)
j
-j
f
Upper sign (-)
Lower sign (+)
Where


1
ht  
t
f 0
f 0
USSB
LSSB
Single Sideband Signal
Proof: Fourier transform of the complex envelope




G  f   Ac M  f   j mˆ t   Ac M  f   jMˆ ( f )
Using
ˆ t   mt  ht 
m
2 Ac M  f ,
G f   
0,
Recall from Chapter 4
Upper sign  USSB
Lower sign  LSSB
 G f   Ac M  f 1  jH  f 
f  0

f  0
V( f ) 
1
G( f  f c )  G * [( f  f c )]
2
f   fc 
M  f  f c , f  f c 
0,
S  f   Ac 

A


c


0
,
f

f
M
f

f
,
f


f
c
c
c 


Upper sign  USSB
If lower signs were used  LSSB signal would have been obtained
Single Sideband Signal
2 Ac M  f ,
G f   
0,
f  0

f  0
 M  f  f c  , f  f c 
S  f   Ac 

f  f c 
0,
f   f c 
0,
Ac 

M
f

f
,
f


f

c
c
 
SSB - Power
The normalized average power of the SSB signal
s 2 t  
1
1
2
2
g (t )  Ac2 m 2 t   mˆ t 
2
2
Hilbert transform does not change
power.
SSB signal power is:
2
mˆ t   m 2 t 
s 2 t   Ac2 m 2 t 
Power gain factor
The normalized peak envelope (PEP) power is:
1
1 2 2
2
2
max g (t )  Ac m t   mˆ t 
2
2
Power of the modulating signal
Generation of SSB
SSB signals have both AM and PM.
The complex envelope of SSB:
ˆ t 
g t   Ac mt   jm
For the AM component,
ˆ t 
Rt   g t   Ac m 2 t   m
For the PM component,
2
 mˆ t 
 t   g t   tan 

 mt  
1
Advantages of SSB
• Superior detected signal-to-noise ratio compared to that of AM
• SSB has one-half the bandwidth of AM or DSB-SC signals
Generation of SSB
•
SSB Can be generated using two techniques
1. Phasing method
2. Filter Method
•
Phasing methodg t   Ac mt   jmˆ t 
This method is a special modulation type of IQ canonical form
of Generalized transmitters discussed in Chapter 4 ( Fig 4.28)
Generation of SSB
•
Filter Method
The filtering method is a special case in which RF processing (with a
sideband filter) is used to form the equivalent g(t), instead of using
baseband processing to generate g(m) directly. The filter method is
the
most popular method because excellent sideband suppression can be
obtained when a crystal oscillator is used for the sideband filter.
Crystal filters are relatively inexpensive when produced in quantity at
standard IF frequencies.
Weaver’s Method for Generating SSB.
Generation of VSB
Frequency Divison Multiplexing
AM, FM, and Digital Modulated Systems






Phase Modulation (PM)
Frequency Modulation (FM)
Generation of PM and FM
Spectrum of PM and FM
Carson’s Rule
Narrowband FM
AM and FM Modulation
(a) Carrier wave.
(b) Sinusoidal modulating signal.
(c) Amplitude-modulated signal.
(d) Frequency modulated signal.
Angle Modulation
 We have seen that an AM signal can be represented as
s(t )  Ac [1  m(t )] cos c t
Note that in this type of modulation the amplitude of signal carries information.
 Now we will see that information can also be carried in the angle of the
signal as
st   Ac cos c t   t 
Here the amplitude Ac remains constant and the angle is modulated.
This Modulation Technique is called the Angle Modulation
Angle modulation: Vary either the Phase or the Frequency of the carrier signal
 Phase Modulation and Frequency Modulation are special cases of Angle
Modulation
Angle Modulation
Representation of PM and FM signals:
The Complex Envelope for an Angle Modulation is given by
g t   Ac e j t 
Rt   g t   Ac Is a constant Real envelope,
θ(t) - linear function of the modulating signal m(t)
g(t) - Nonlinear function of the modulation.
The Angle-modulated Signal in time domain is given by
st   Ac cos c t   t 
Special Case 1:
For PM the phase is directly proportional to the modulating signal. i.e.;
Where Dp is the Phase sensitivity of the phase modulator, having units of radians/volt.
Special Case 2:
For FM, the phase is proportional to the integral of m(t) so that
where the frequency deviation constant Df has units of radians/volt-sec.
Angle Modulation
 Instantaneous Frequency (fi) of a signal is defined by
d t 


i t 
  t     i ( ) d
dt

t
where  t   ct   (t )
 Phase Modulation occurs when the instantaneous phase varied in proportion to that of
the message signal.
 t   D p mt 
Resulting PM wave:
Dp is the phase sensitivity of the modulator
s (t )  Ac cos[ c t  D p m(t )]
 Frequency Modulation occurs when the instantaneous frequency is varied linearly
with the message signal.
 i (t )   c  D f m(t )
 t   D f
t
 m d
Df is the frequency
deviation constant

Resulting FM wave:
s(t )  Ac cos[ c t  D f
t
 m( ) d ]

Phase and Frequency Modulations
• Frequency Modulation
• Phase Modulation
Comparing above two equations , we see that if we have a PM signal modulated
by mp(t), there is also FM on the signal, corresponding to a different modulation
wave shape that is given by:
Similarly if we have a FM signal modulated by mf(t),the corresponding phase
modulation on this signal is:
Where f and p denote frequency
and phase respectively.
Generation of FM from PM and vice versa
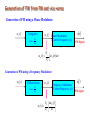
Generation of FM using a Phase Modulator:
m f t 
m p t 
Integrator
Gain 
Phase Modulator
(Carrier Frequency fc)
Df
Dp
m p t  
Df
Dp
st 
FM Signal
t
 m  d
f

Generation of PM using a Frequency Modulator:
m p t 
Differentiator
Gain 
Df
Dp
m f t 
Frequency Modulator
(Carrier Frequency fc)
D p  dm p t 
m f t  


D f  dt 
st 
PM signal
FM with sinusoidal modulating signal
 t   ct   (t )
If a bandpass signal is represented by:
1
fi  t   f c 
2
 The Instantaneous Frequency of the FM signal is given by:
 The Frequency Deviation from the carrier frequency:
 The Peak Frequency Deviation is given by:
F  max
∆F is related to the peak modulating voltage by F 
 The Peak-to-peak Deviation is given by
f d t   f i t   f c 
1
2
1
D f Vp
2
 d  t  


dt


1  d t 
2  dt 
 d t 
 dt 
Where
V p  max mt 
 1  d t  
 1  d t  
Fpp  max  

min

 



2

dt
2

dt


 
 
FM with sinusoidal modulating signal
f i t   f c 
1  d t 
2  dt 
But,

Vp

 BW
Average Power does not change
with modulation
Ac2
Average Power 
2
Angle Modulation
Advantages:
 Constant amplitude means Efficient Non-linear Power Amplifiers can be used.
 Superior signal-to-noise ratio can be achieved (compared to AM) if bandwidth is
sufficiently high.
Disadvantages:
 Usually require more bandwidth than AM
 More complicated hardware
Modulation Index
 The Peak Phase Deviation is given by:
  max  t 
∆θ is related to the peak modulating voltage by:   D pV p
 The Phase Modulation Index is given by:
 p  
Where V p  max mt 
Where ∆θ is the peak
phase deviation
 The Frequency Modulation Index is given by:
f 
F
B
∆F Peak Frequency Deviation
B Bandwidth of the modulating signal
Spectra of Angle modulated signals
Spectrum of Angle modulated signal
S f  

Where G  f   g t    Ac e j t 


1
G  f  f c   G   f  f c 
2

 Spectra for AM, DSB-SC, and SSB can be obtained with simple formulas
relating S(f) to M(f).
 But for angle modulation signaling, because g(t) is a nonlinear function of m(t).
Thus, a general formula relating G(f) to M(f) cannot be obtained.
 To evaluate the spectrum for angle-modulated signal, G(f) must be evaluated on a
case-by-case basis for particular modulating waveshape of interest.
Spectrum of PM or FM Signal with Sinusoidal Modulating Signal
 Assume that the modulation on the PM signal is
m p t   Am sin  m t
Then
 t    sin  m t
Where  p  D p Am   is the phase Modulation Index.
Same θ(t) could also be obtained if FM were used
m f t   Am cos mt
where
and
   f  D f Am /  m
The peak frequency deviation would be
F 
1
D f Am
2
The Complex Envelope is:
g t   Ac e
j t 
 Ac e
j sin  m t
which is periodic with period
Tm 
1
fm
Spectrum of PM or FM Signal with Sinusoidal Modulating Signal
Using discrete Fourier series that is valid over all time, g(t) can be written as
g t  
n 
jn m t
c
e
n
n  
Where
Ac
cn 
Tm
 1
c n  Ac 
 2
Which reduces to
 e
Tm 2
j sin m t
Tm 2
e
 jnm t
j   sin  n  
e

  Ac J n  

Jn(β) – Bessel function of the first kind of the nth order
J n     1 J n  
n
Is a special property of Bessel Functions
Taking the fourier transform of the complex envelope g(t), we get
G f  
n 
 c   f  nf 
n  
n
m
or
dt
G  f   Ac
n 
 J      f  nf 
n 
n
m
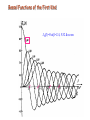
Bessel Functions of the First Kind
J0(β)=0 at β=2.4, 5.52 & so on

Bessel Functions of the First Kind
Frequency spectrum of FM
 The FM modulated signal in time domain
S (t )  Ac

J
n  
n
(  ) cos[( c  n m )t ]
Observations:
 From this equation it can be seen that the frequency spectrum of an FM
waveform with a sinusoidal modulating signal is a discrete frequency
spectrum made up of components spaced at frequencies of c± nm.
 By analogy with AM modulation, these frequency components are called
sidebands.
 We can see that the expression for s(t) is an infinite series. Therefore the
frequency spectrum of an FM signal has an infinite number of sidebands.
The amplitudes of the carrier and sidebands of an FM signal are given by
the corresponding Bessel functions, which are themselves functions of the
modulation index
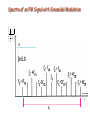
Spectra of an FM Signal with Sinusoidal Modulation
 The following spectra show the effect of modulation index, , on the
bandwidth of an FM signal, and the relative amplitudes of the carrier and
sidebands


 S( f ) 


 1A 

c 
 2

1.0
f
BT
Spectra of an FM Signal with Sinusoidal Modulation


 S( f ) 


 1A 

c 
 2

J0(1.0)
1.0
J1(1.0)
J2(1.0)
f
BT
Spectra of an FM Signal with Sinusoidal Modulation


 S( f ) 


1
 A 

c 
 2

1.0
f
BT
Carson’s rule
 Although the sidebands of an FM signal extend to infinity, it has been found
experimentally that signal distortion is negligible for a bandlimited FM signal
if 98% of the signal power is transmitted.
 Based on the Bessel Functions, 98% of the power will be transmitted when
the number of sidebands transmitted is 1+ on each side.
(1+fm
Carson’s rule
 Therefore the Bandwidth required is given by
BT  2    1 B
β – phase modulation index/ frequency modulation index
B – bandwidth of the modulating signal
For sinusoidal modulation
B  fm
 Carson’s rule : Bandwidth of an FM signal is given by
BT  2  1 f m
Note: When β =0 i.e. baseband signals
BT  2 f m
Narrowband Angle Modulation
 Narrowband Angle Modulation is a special case of angle modulation where θ(t) is
restricted to a small value.
 (t )  0.2 rad
 The complex envelope can be approximated by a Taylor's series in which only first
two terms are used.
g t   Ac e j
becomes
g t   Ac 1  j t 
 The Narrowband Angle Modulated Signal is
[ because
e x  1  x for x  1]
st   Ac cos ct  Ac t sin ct
 The Spectrum of Narrowband Angle Modulated Signal is
Ac


  f  f c     f  f c   j f  f c    f  f c 
S f 
2
where
 D p M  f ,

 f    t    D f
 j 2f M  f .

PM
FM
Indirect method of generating WBFM
Balanced Modulator
st   Ac cos ct  Ac t sin ct
Wideband Frequency modulation
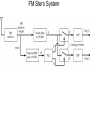
FM Stero System
FM Stero System
AM, FM, and Digital Modulated Systems




Binary Bandpass Signalling Techniques
OOK
BPSK
FSK
Binary Bandpass Signaling techniques
 On–Off keying (OOK) [amplitude shift keying (ASK)] - Consists of keying (switching) a
carrier sinusoid on and off with a unipolar binary signal.
- Morse code radio transmission is an example of this technique.
- OOK was one of the first modulation techniques to be used and precedes
communication systems.
analog
 Binary Phase-Shift Keying (BPSK) - Consists of shifting the phase of a sinusoidal carrier
0o or 180o with a unipolar binary signal.
- BPSK is equivalent to PM signaling with a digital waveform.
 Frequency-Shift Keying (FSK) - Consists of shifting the frequency of a sinusoidal carrier
from a mark frequency (binary 1) to a space frequency (binary 0), according to the baseband
digital signal.
- FSK is identical to modulating an FM carrier with a binary digital signal.
Binary Bandpass Signaling techniques
On-Off Keying (OOK)
 Also known as Amplitude Shift Keying (ASK)
Carrier
Cos(2fct)
Message
m(t)
OOK output
Acm(t)Cos(2fct)
 The complex envelope is
g t   Ac mt 
 The OOK signal is represented by
st   Ac mt cos  c t
 The PSD of this complex envelope is given by
2
 sin fTb  
Ac2 
 
  f   Tb 
g  f  
2 
 fTb  

where m(t) has a peak value of A  2
2
So that s(t) has an average normalized power of Ac
2
On-Off Keying (OOK)
Tb 
1
Message
Unipolar
Modulation
m(t)
Bipolar
Modulation
m(t)
OOK signal
s(t)
Tb – bit period ;
0
1
0
1
R – bit rate
0
1
1
R
On-Off Keying (OOK)
 PSD of the bandpass waveform is given by
Pv ( f ) 


1
Pg  f  f c   Pg  f  f c 
4
 Null-to-Null bandwidth is BT  2R and absolute bandwidth is BT  
 The Transmission bandwidth is BT  2B
Where B is the baseband bandwidth
Detection of OOK
 Non-Coherent Detection
OOK in
Binary output
Envelope
Detector
 Coherent Detection with Low-pass filter
Ac m(t ) cos 2 (2 f c t )
OOK in
s(t )  Ac m(t ) cos(2 f c t )
cos(2 f c t )
LPF
Binary output
1
Ac m(t )
2
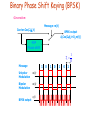
Binary Phase Shift Keying (BPSK)
Generation:
Message: m(t)
Carrier:Cos(2fct)
BPSK output
AcCos(2fct+Dpm(t))
-90
Phase shift
1
Tb 
R
1
Message
Unipolar
Modulation
m(t)
Bipolar
Modulation
m(t)
BPSK output
s(t)
0
1
0
1
0
1
Binary Phase Shift Keying (BPSK)
 The BPSK signal is represented by
let


 A cosD mt cos  t  A sin D mt sin  t
 A cos D cos  t  A sin D mt sin  t
st   Ac cos  c t  D p mt 
c
p
c
c
p
c
c
p
c
p
pilot carrier term
m(t )  1
c
c
data term
 The level of the pilot carrier term is set by the value of the peak deviation
 The digital modulation index ‘h’ is given by
h
2
2∆θ – maximum peak-to-peak
deviation during time Ts

 If Dp is small, then there is little power in data term & more in pilot term
 To maximize performance (minimum probability of error)
Optimum case :   D p  90 0  
2
BPSK signal : st    Ac mt sin  c t
Binary Phase Shift Keying (BPSK)
 The complex envelope for this BPSK is given by
g t   jAc mt 
 The PSD for this complex envelope is given by
 sin fTb 

g  f   Ac2Tb 
 fTb 
 PSD of the bandpass waveform is given by
Pv ( f ) 


1
Pg  f  f c   Pg  f  f c 
4
Average normalized
power of s(t) : Ac2 2
Null-to-Null
BW
PSD of optimum BPSK
Binary Phase Shift Keying (BPSK)
Power Spectral Density (PSD) of BPSK:
If Dp  /2
Pilot exists
Ac2  sin(  ( f  f c ) / R) 


8R   ( f  f c ) / R 
fc
2R = 2/Tb
2
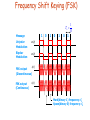
Frequency Shift Keying (FSK)
 Discontinuous FSK :
Osc. f1
Osc. f2
Cos(2f1t)
Message: m(t)
Cos(2f2t)
FSK output
AcCos(2f1t+1) or
AcCos(2f2t+2)
 The discontinuous-phase FSK signal is represented by
 Ac cos1t  1 , for t in the time interval when a binary '1' is sent
st   Ac cosc t   t   
 Ac cos 2 t   2 , for t in the time interval when a binary '0' is sent
 t  1   c t
 t    1
 2 t   2   c t
for t during a binary ‘1’ signal
for t during a binary ‘0’ signal
Frequency Shift Keying (FSK)
 Continuous FSK :
Message: m(t)
FSK output
Frequency
Modulator
fc
t


Ac cos 2f c t  D f  m d 



 The Continuous-phase FSK signal is represented by
or
where

st   Ac cos  c t  D f




m

d




t

st   Re g t e jct

g t   Ac e j t 
 t   D f
t
 m d

for FSK
Frequency Shift Keying (FSK)
Tb 
1
Message
Unipolar
Modulation
m(t)
Bipolar
Modulation
m(t)
0
1
0
1
0
1
R
1
s(t)
FSK output
(Discontinuous)
FSK output
(Continuous)
s(t)
Mark(binary 1) frequency: f1
Space(binary 0) frequency: f2
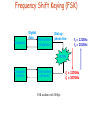
Frequency Shift Keying (FSK)
Computer
Digital
data
FSK modem
(Originate)
Dial up
phone line
f1 = 2225Hz
f2 = 2025Hz
PSTN
Computer
Center
FSK modem
(Answer)
FSK modem with 300bps
f1 = 1270Hz
f2 = 1070Hz
END